基于Fisher判别的改进WFCM 分割算法
2015-12-23郑金志曾绍华曾凡玉
郑金志,曾绍华,曾凡玉,龙 颖
(1.重庆师范大学 计算机与信息科学学院,重庆401331;2.重庆师范大学 模式分析与信息处理研究所,重庆401331)
0 引 言
传统的FCM 算法分割图像通常存在几个缺点[1]:①初始化不当导致算法收敛到局部最优解;②算法运行耗时,FCM 分割图像无法满足工程实践的实时性要求;③算法没有考虑聚类像素的空间信息,对噪声比较敏感。因此,高新波、Abbas Biniaz等学者提出了改进的FCM 算法[1-7]解决图像信息量大、分割耗时的问题,取得了一定的效果,不过,改善的效率较为有限。刘健等学者提出基于GLCM 特征的改进FCM 图像分割算法[8],将GLCM 和粒子群优化算法引入到FCM 算法中较好解决了初始聚类中心不易确定的问题,但是该算法较为耗时。Zulaikha Beevi、彭代强等学者提出了改进FCM 算法[9,10],期望解决算法本身对图像噪声敏感的问题。这些的改进算法对每一个像素的空间信息进行处理,一定程度上改善了噪声对图像分割结果的影响,但对正常像素点做抑噪处理浪费了大量的时间,且随图像噪声的增加,分割效果显著降低。
由于电路板加工、生产等环境中有很强的静电脉冲和摄像设备本身的因素等原因,电路板图像含有较多的椒盐噪声。对噪声图像的分割可以在分割前先进行滤噪,但是这种把抑噪和分割分开的方法会增加噪声图像的分割时间,无法满足电路板图像检测中对实时性和抑噪能力的要求,尚需进一步改进。
本文基于WFCM 对椒盐噪声图像的分割主要做两方面的工作:①构造最优化问题,优化初始聚类中心,以期减少算法运行时间和迭代次数,改善算法的时间效率;②引入噪声像素点的空间信息,在减少算法对噪声敏感的同时,尽可能提高算法的时间效率。
1 加权模糊c均值聚类 (WFCM)算法
高新波等提出一种WFCM (加权模糊C 均值)聚类算法[2]。其思想是:对于灰度图像,将像素点的灰度值投影到256个灰度级上,算法聚类的对象不再是像素点,而是图像在256个灰度级上的投影;每一灰度级对应的直方图函数值为样本聚类权值。
WFCM 算法[2]:设将有效灰度级集G ={0,1,2,…,255}分为C 类。定义图像f(x,y)的归一化直方图函数
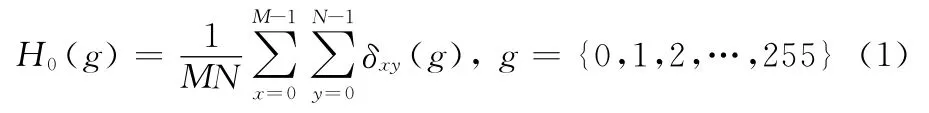
建立WFCM 关于隶属度矩阵U 和聚类中心V 的最优化问题[2]
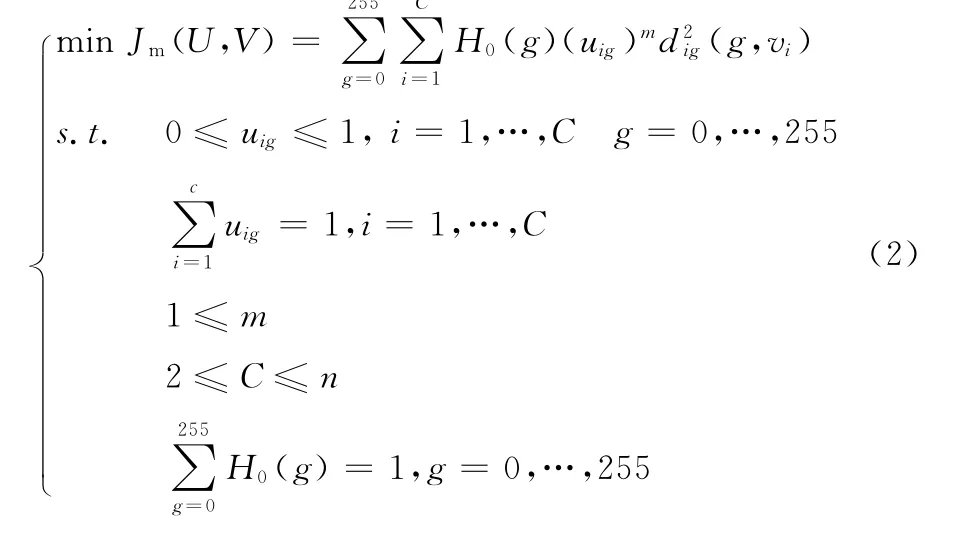
式中:C——分类数,H0(g)——灰度级g 的权值,uig——灰度级g 对第i类的隶属度,m——模糊指数,也称为平滑参数,用其来调节聚类的模糊程度。向量V ={v1,v2,…,vC}为C 类各自的聚类中心,dik(g,vi)为灰度级g 离第i类聚类中心的距离。
应用拉格朗日乘数法求解,获得隶属度矩阵U 和聚类中心向量V 的迭代算子[2]
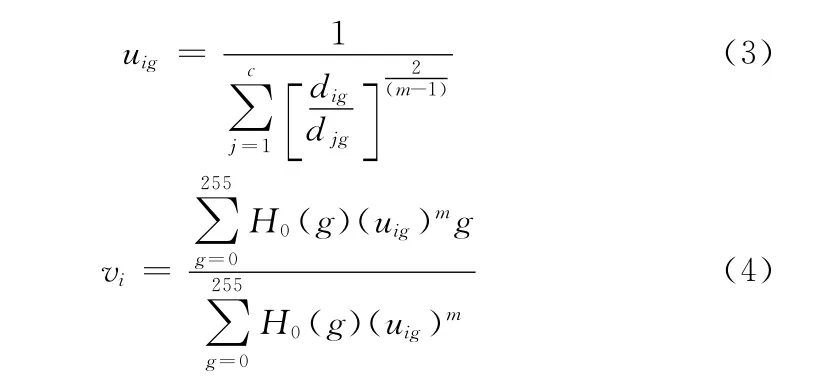
WFCM 算法描述如下:
算法1:WFCM[2]算法

输入(1)M×N 的图像像素点集合f ={f(x,y)|f(x,y),x,y ∈N;0≤f(x,y)≤255,1≤x ≤M,1≤x ≤N}(2)灰度级集合G ={0,1,2,…,255}初始化(1)终止阈值T、加权指数m、聚类数C、迭代计数器P=0;(2)初始聚类中心向量V(p)赋随机值;过程(1)用式 (1)计算集合f(x,y)的直方图H0(G);(2)do{ 1)用G 和V(p)计算欧氏距离矩阵 D ={dig = g-v(i) }; 2)更新迭代计数器P =P+1; 3)用式 (3)计算隶属度矩阵U(p); 4)用式 (4)计算聚类中心V(p);}while V(p)—V(p-1) ≥(T )输出(1)隶属度矩阵U =U(p);(2)聚类中心V =V(p);(3)迭代次数P;
2 改进的WFCM 算法
高新波[2]等提出的WFCM 算法,采用随机数初始化聚类中心或隶属度矩阵,缺乏科学合理性;存在初始值的不同、分类结果、迭代次数可能不一致,运行进程和结果严重依赖于初始值的问题;算法没有考虑像素点的空间信息,分割结果对图像噪声敏感。因此,为了满足含椒盐噪声电路图像分割的工程实践要求,需要对WFCM 进行改进。
2.1 根据噪声图像粗略复原直方图
理论上灰度直方图应是多峰函数,基于WFCM 的图像分割算法假定背景和目标在直方图中对应不同的波峰[2],然而实际图像中,由于噪声的污染使得直方图的波峰波谷不再明显,直方图的波峰波谷不能很好的代表图像目标与背景的区分关系[2]。本文在电路图像分割前,首先粗略恢复其直方图。
2.1.1 计算图像噪声率
Kenny等[11]提出对于灰度图像把灰度值为0和255的像素点定义为椒盐噪声点。对M×N 被椒盐噪声污染的电路图像f(x,y),f(x,y)∈ {0,1,2,…,255}是像素点(x,y)处的灰度值。定义噪声率
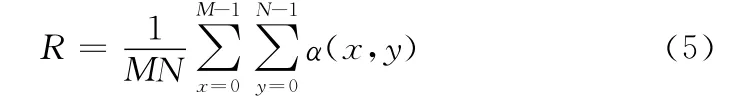
2.1.2 直方图的粗略复原
蔡利栋提出了一种椒盐噪声图像的原始图像直方图粗略复原方法[12]
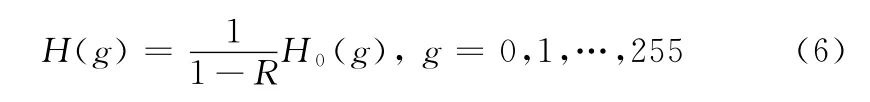
式中:H0(g)——噪声图像的直方图函数,R——图像的噪声率。
2.2 初始聚类中心的确定
2.2.1 确定初始聚类中心的思想
根据电路图像分割的先验知识,确定图像分割的类数C。采用文献 [13,14]的方法构造复原直方图H(g)势函数,找出C-1个波谷点作为势直方图分割点,将该直方图分割为C 段。由于背景和目标在直方图中对应不同的波峰[11],从C 段中分别找出C 类的初始聚类中心有利于避免算法收敛到局部最优解处。
假设直方图的C 段对应C 类分割目标,再依据Fisher[15,16]判别思想 “类间离差尽可能大,类内离差尽可能小”构造确定C 类重心 (初始聚类中心)的最优化问题,最终确定模糊聚类的初始聚类中心V(0)。
设图像中的有效灰度级G ={0,1,2,…,255}为分类样本,灰度值g 的样本权重为H0(g),待定系数为λ,则每个有效灰度级与λ相乘
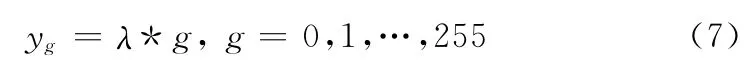
总体重心为
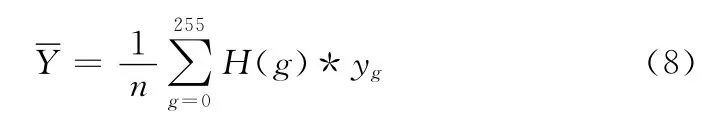
则第i类的重心为
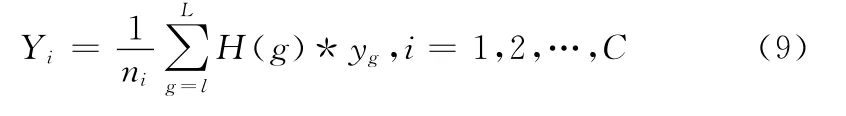
第i类的类内离差平方和为
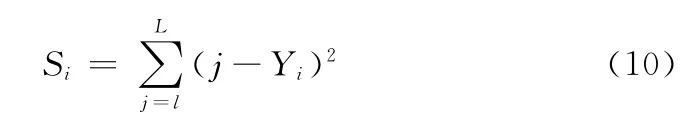
类内离差平方总和为

类间离差平方总和为
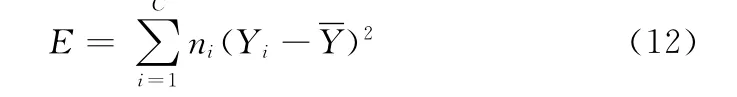
获得最优化问题
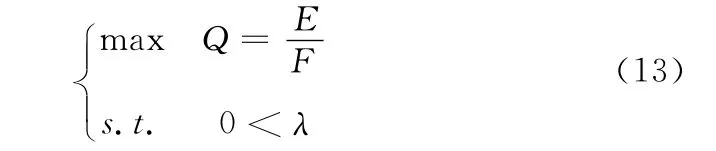
求解最优化式 (13),将λ带入式 (9),求出C 类重心Yi,作为初始聚类中心V(0)。
2.2.2 确定初始聚类中心算法
依据2.2.1的算法思想,确定初始聚类中心算法描述如下:
算法2:确定初始聚类中心的算法

输入(1)M×N 图像的像素点集合f ={f(x,y)|f(x,y),x,y ∈N;0≤f(x,y)≤255,1≤x ≤M,1≤y ≤N};(2)灰度级集合G ={0,2,…,255};初始化 (1)分类类别数C,待定系数为λ;(1)用式 (1)计算集合f(x,y)的直方图H0(G);(2)用式 (6)复原原始直方图H(G);(3)用文献 [13,14]中方法构造复原直方图H(G)的势函数,找出C-1个波谷点,作为分割点;(4)用式 (7)和式 (8)计算总体重心过程Y;(5)for(i=1to C){ 1)用式 (9)计算第i类的重心Yi; 2)用式 (10)计算第i类的类内离差平方和Si;}(6)用式 (11)计算类内离差平方总和F;(7)用式 (12)计算类间离差平方总和E;(8)根据最优化问题 (13),求解λ;(9)for(i=1to C){ 1)将λ带入式 (7)计算yg; 2)用式 (9)计算第i类的重心Yi;}输出 (1)初始聚类重心V(0)={Y1,Y2,…,YC };
2.3 改进WFCM 算法
为了抑制噪声对分割结果的影响,一些学者根据像素的空间信息提出改进算法[6,7,9,10],一定程度上降低算法对噪声的敏感性。但它们未区分噪声点和正常点,对噪声点做迭代聚类、信息点做抑噪处理,会耗费计算时间,因此,WFCM 对椒盐噪声图像的分割效果尚可进一步改进。
2.3.1 改进算法思想
首先按照Kenny等提出的方法[11],区分椒盐噪声点和正常像素点;使用2.2 的方法确定初始聚类中心。然后,对正常像素点结合噪声图像直方图用算法1进行聚类分割,得到正常像素点的空间隶属度矩阵。最后,对噪声点fg,如果它邻域内的正常像素点离第i类聚类中心vi的距离较近,则视为fg离第i类聚类中心vi的距离也较小。定义噪声像素点fg隶属于第i类的隶属度
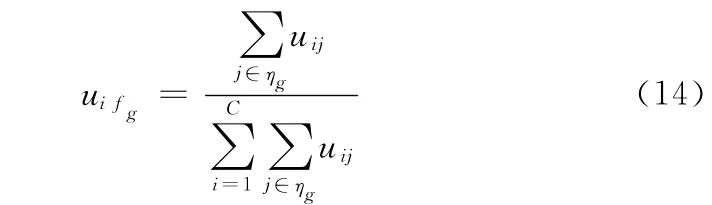
式中:uifg——fg对于聚类中心vi的隶属度,ηg——fg领域中值不为0或255的所有像素点集合。
2.3.2 改进WFCM 算法
依据2.3.1的算法设计思想,改进WFCM 算法描述如下:
算法3:改进的WFCM 聚类算法

注:邻域ηg 的大小为奇数;算法3中设定的分数C与算法2中分类数C是一致的。
利用隶属度矩阵最大化的原则,硬化软分割的隶属度矩阵U ,得到图像分割结果。
3 仿真实验
3.1 仿真实验样本的获取
在实验室环境中,将卡西欧EX-ZS26型数码相机固定在垂直距离PCB电路板10cm 处,自动对焦的模式下采集两张PCB图像作为实验数据,实验照度范围129.5-168.8lx。
为了减少计算,从原始图像中随机切割出两张大小分别为256×320和512×640图像区域。由于图像被相机自带的滤波器处理,实验样本图1 (a)、 (b)和 (c)分别是添加6%、20%和30%随机椒盐噪声的图像。

图1 实验图像
3.2 仿真实验
仿真实验环境:Win7 (32bit),系统内存为4G,CPU为Intel(R)Core(TM)i5,主频2.60GHz,Intel(R)HD Graphics 4000集成显卡,MATLAB R2010b(32bit)。
3.2.1 恢复直方图、获取初始聚类中心及实验分析
实验假设图像噪声率未知道的情况下,利用算法2对图1 (a)、图1 (b)和图1 (c)复原直方图如图2所示,计算初始聚类中心的相关数据见表1。势直方图寻找波峰波谷的过程张新明等学者都做了详细论述[13,14],本文不再对相关结论进行论证。
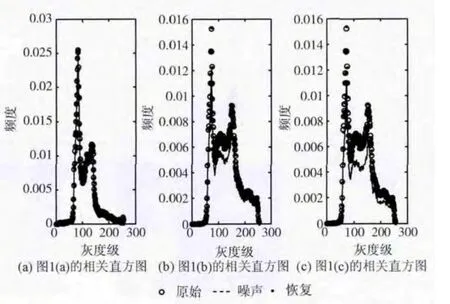
图2 恢复直方图与原始图像直方图的比较
图2显示,噪声率较低时噪声图像直方图与原始图像直方图较为接近,此时噪声点对原始图像直方图波峰波谷的影响较小;当噪声率较大时,噪声点对原始图像直方图波峰波谷的影响较大,算法2对原始图像直方图的复原能够较好的模拟原始图像直方图,因此有利于波峰波谷的划分。从表1中的数据可以看出,算法2对图1 (a)确定的4个初始聚类中心,与最终求得聚类中心最大相差3个灰度级;对图1 (b)和图1 (c)确定的3个初始聚类中心,与最终获得的聚类中心也分别最大相差23个和24个灰度级。图1 (b)和图1 (c)在获取初始聚类中心过程中所得的数据比较接近,表明算法2有较强的抗椒盐噪声能力。

表1 算法2获取初始聚类中心的相关数据
3.2.2 部分仿真实验分割图像及分析
Nikhil等提出,聚类模糊指数m 的取值范围一般为[1.5,2.5],通常取m =2时较为合适[17]。本文实验设置m =2,迭代停止阈值T =1×10-5,设置噪声点处理的邻域大小为3×3,图1 (a)分类数C =4,图1 (b)和图1(c)分类数C =3。部分仿真实验结果的量化数据见表2,分割结果如图3所示。
对比图3与图1 (a)可以看出WFCM[2]算法没有任何抑噪的能力,对噪声比较敏感;对比图3 (a)与(b)、(d)与图3 (e)、(g)与图3 (h)可以看到,图3 (b)、(e)、(h)的分割结果要稍微优于图3 (a)、 (d)、 (g) (如,图 (b)分割结果集成电路上的黑色噪声点要少于图 (a)分割结果对应集成电路上的黑色噪声点),但是依然有较强的噪声,由此可以得出,FFCM[18]算法具有一定的抑噪能力,但是抑噪能力十分有限。图3 (c)是本文算法对图1 (a)的分割结果,对比图3 (a)、(b)与图3 (c)3幅分割结果可以看出,当噪声率达到6%时,本文算法能够正确完成图像分割任务。
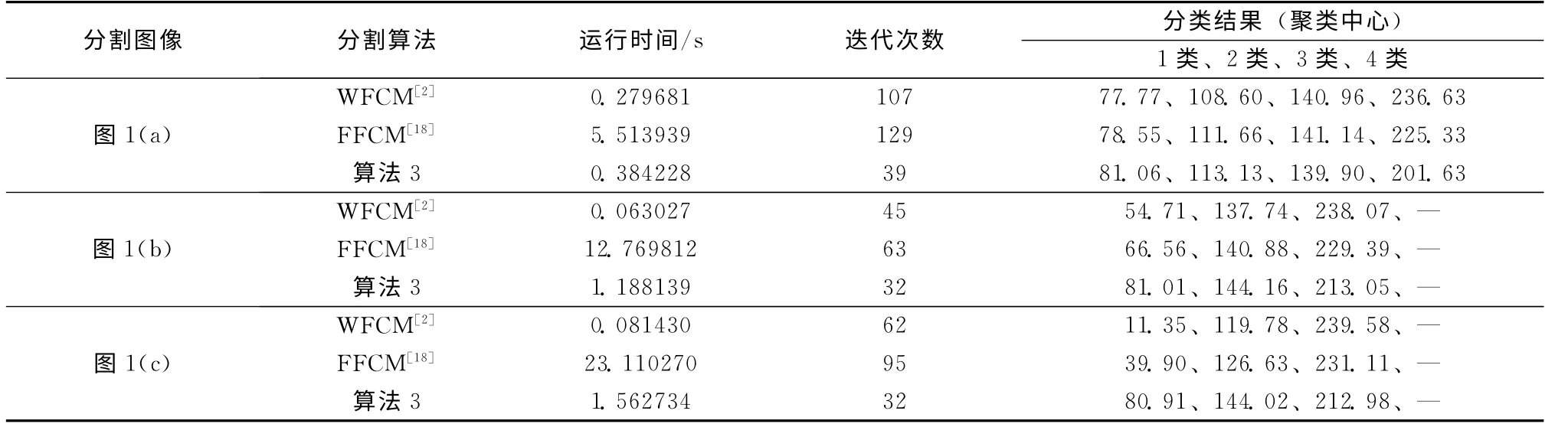
表2 3种方法对图像分割结果及性能的比较

图3 3种算法对图1分割效果的对比
由图3中3种算法对含20%椒盐噪声图1 (b)的分割结果图3 (d)、(e)、 (f)可以看到,WFCM[2]算法和FFCM[18]算法虽然仍能完成分割任务,但是FFCM[18]算法的抑噪能力有较大的衰减,而本文算法不仅能够完成分割任务,且其分割结果几乎不受噪声影响。
图3中 (g)、(h)、(i)是3种算法对含30%椒盐噪声的图1 (c)分割结果。可以看出WFCM[2]算法和FFCM[18]算法不仅无法对噪声点进行分割,而且也无法完成对像素信息点的正确分割。此外,FFCM[18]算法的抑噪能力几乎完全丧失。这是因为在聚类分割过程中噪声点对信息点造成了干扰。由本文算法对图1 (c)的分割结果可以看到,该算法不仅能够对图像进行正确的分割,而且仍然具有较强的抑噪能力。
由图3 (c)、(f)、 (i)可以得出:当噪声率达到20%时,本文算法的分割结果几乎不受噪声的影响;当噪声率达到30%时,本文算法的抑噪能力有所衰减,但是依然表现出了较强的抑噪性能,这证明随着噪声率的快速增加,本文算法的抑噪性能衰减较少。
表2中的运行时间为算法整体运行时间,包括预处理阶段和循环迭代阶段的时间总和;其中WFCM 算法[2]和FFCM 算法[18]因初始聚类中心的随机化使得每次运行时间不同,表2中的数据是各自运行20次的平均值。
仿真结果表2中数据显示:算法3因从更科学合理的初始聚类中心出发,迭代次数减少;因做抑噪处理,比WFCM[2]算法运行时间稍高,但仅牺牲较少的时间效率,增强了算法的抗噪能力。
算法3相对于FFCM[18]算法,不仅从更科学合理的初始聚类中心出发减少迭代步骤、提高算法的时间效率、使分割结果收敛到全局最优解;同时还省去了对正常像素点进行抑噪和对噪声点进行迭代聚类的冗余处理,进一步减少了迭代次数,提高了算法的时间效率。
4 结束语
针对在工业生产加工过程中电路板 (PCB)图像含有较多椒盐噪声这一特性,本文提出了基于Fisher思想的改进WFCM 图像分割算法。针对FCM 算法迭代较为耗时以及对噪声较为敏感等缺点,根据Fisher判别的思想建立优化初始聚类中心的模型,合理地初始化WFCM 聚类中心。然后,对图像信息点和噪声点进行初步判别,精简参加迭代聚类的数据集,提高迭代聚类的时间效率。最后,根据噪声点空间信息,对噪声点进行分割处理,完成对整幅图像的分割。改进算法不仅能避免噪声点对信息点迭代聚类的干扰,而且能抑制噪声点对图像分割的影响,具有较强的抑噪能力和较高的时间效率。仿真结果表明,本文算法相对于经典WFCM 算法和FFCM 算法[18],具有更高的时间效率和抑噪性能。
[1]CUI Zhaohua,GAO liqun,OUYANG Haibin,et al.Improved fuzzy c-means clustering combined with the global best harmony search algorithm for image segmentation [J].Journal of Image and Graphics,2013,18 (19):1133-11141 (in Chinese).[崔兆华,高立群,欧阳海滨,等.融合全局最好和声搜索算法的模糊C 均值聚类图像分割 [J].中国图象图形学报,2013,18 (19):1133-1141.]
[2]GAO Xinbo,LI Jie,JI Hongbing.A multi-threshold image segmentation algorithm based on weighting fuzzy C-means clustering and statistical test[J].Acta Electronica Sinica,2004,32 (4):661-664 (in Chinese).[高新波,李洁,姬红兵.基于加权模糊C均值聚类与统计检验指导的多阈值图像自动分割算法 [J].电子学报,2004,32 (4):661-664.]
[3]Mohamed Ali Mahjoub.Improved FCM algorithm applied to color image segmentation [J].Canadian Journal on Image Processing and Computer Vision,2011,2 (2):16-19.
[4]LI Xuchao,LIU Haikuan,WANG Fei,et al.The survey of fuzzy clustering method for image segmentation [J].Journal of Image and Graphics,2012,17 (4):447-458 (in Chinese).[李旭超,刘海宽,王飞,等.图像分割中的模糊聚类方法[J].中国图象图形学报,2012,17 (4):447-458.]
[5]Ji Zexuan,Sun Quansen,Xia Deshen.A framework with modified fast FCM for brain MR images segmentation [J].Pattern Recognition,2011,44 (5):999-1013.
[6]Xu Shaoping,LIU Xiaoping,LI Chunquan et al.An improved fast FCM image segmentation algorithm base on region feature analysis[J].Pattern Recongnition and Artificial Intellignece,2012,25 (6):987-995.
[7]Abbas Biniaz,Ataollah Abbasi,Mosa Shamsi.Fast FCM algorithm for brain MR image segmentation [C]//6th International Conference on Fuzzy Information and Engineering,2012:1-8.
[8]LIU Jian,CHENG Yinglei,SUN Jida.Modified FCM SAR image segmentation method based on GLCM feature[J].Computer Engineering and Design,2012,33 (9):3502-3506 (in Chinese).[刘建,程英蕾,孙纪达.基于GLCM 特征的改进FCM 的SAR 图像分割方法 [J].计算机工程与设计,2012,33 (9):3502-3506.]
[9]Zulaikha Beevi S,Mohammed Sathik M,Senthamer Aikannan K.A robust fuzzy clustering technique with spatial neighborhood information for effective medical image segmentation [J].International Journal of Computer Science and Information Security,2010,7 (3):132-138.
[10]WANG Haijun,LIU Ming.Generalized fuzzy c-means algorithm with improved fuzzy partition based on local membership and neighbor information [J].Journal of Computer Applications,2013,33 (8):2355-2358 (in Chinese). [王海军,柳明.基于局部隶属度和邻域信息的GIFP-FCM 图像分割算法 [J].计算机应用,2013,33 (8):2355-2358.]
[11]Kenny KVT,Nor AM Isa.Noise adaptive fuzzy switching median filter salt and pepper noise reduction [J].IEEE Signal Processing Letters,2010,17 (13):281-284.
[12]CAI Lidong.Behavior of image histogram under pepper-andsalt noise [J].Computer Engineering&Science,2008,30(11):25-27 (in Chinese). [蔡利栋.椒盐噪声下图像直方图的行为 [J].计算机工程与科学,2008,30 (11):25-27.]
[13]ZHANG Xinming,LI Zhenyun,ZHENG Ying.Multi-threshold image segmentation based on combining Fisher criterion and potential function [J].Journal of Computer Applications,2012,32 (10):2843-2847 (in Chinese). [张新明,李振云,郑颖.融合Fisher准则和势函数的多阈值图像分割 [J].计算机应用,2012,32 (10):2843-2847.]
[14]BAY H,ESS A,Tuytelaarst.Speeded-up robust features[J].Computer Vision and Image Understanding,2008,110(3):346-359.
[15]WEN Qiaonong,WAN Suiren,XU Shuang.Noise image segmentation using Fisher criterion and regularization level set method [J].Journal of Computer Research and Development,2012,49 (6):1339-1347 (in Chinese).[文乔农,万遂人,徐双.Fisher准则和正交化水平集方法分割噪声图像 [J].计算机研究与发展,2012,49 (6):1339-1347.]
[16]WANG Xin,LIU Ying,FAN Jiulun.Face feature extraction based on weighed multiple kernel Fisher discriminant analysis[J].Computer Science,2012,39 (9):262-247 (in Chinese).[王昕,刘颖,范九伦.基于多核Fisher判别分析的人脸特征提取 [J].计算机科学,2012,39 (9):262-247.]
[17]PR Nikhin JC Bezdek.On cluster validity for fuzzy C-means model[J].IEEE Transactions on Fuzzy Systems,1995,3(3):370-379.
[18]LI Zhimei,XIAO Degui.An improved image segmentation algorithm of fast fuzzy clustering [J].Computer Simulation,2009,26 (8):212-215 (in Chinese). [李志梅,肖德贵.改进的快速模糊聚类图象分割算法 [J].计算机仿真,2009,26 (8):212-215.]
