LabVIEW在灰色GM (1,1)模型测量过程中的应用

LabVIEW在灰色GM (1,1)模型测量过程中的应用*

李金玉

(河南机电高等专科学校 自动控制系，河南 新乡 453000)

摘要:利用LabVIEW强大的数据处理功能与灰色GM(1,1)模型相结合,开发了一个基于LabVIEW的可视化测试平台,将复杂的数学计算过程用程序框图来实现,大大简化了灰色预测计算时间,为工程和非工程人员提供了方便。

关键词:灰色理论；数据预测；LabVIEW

中图分类号：TP274

收稿日期：*2015-04-05

作者简介：李金玉(1982-)，男,河南新乡人,助教,主要从事计算机控制、智能控制方面的研究

0引言

LabVIEW(Laboratory Virtual Instrument Engineering Workbench)是一种程序开发环境,由美国国家仪器(NI)公司研制开发的,类似于C和BASIC开发环境,但是LabVIEW与其他计算机语言的显著区别是:其他计算机语言都是采用基于文本的语言产生代码,而LabVIEW使用的是图形化编辑语言G编写程序产生的程序是框图的形式。使用这种语言编程时,基本上不写程序代码,取而代之的是流程图或框图。它尽可能利用了技术人员、科学家、工程师所熟悉的术语、图标和概念,因此,LabVIEW是一个面向最终用户的工具。它可以增强你构建自己的科学和工程系统的能力,提供了实现仪器编程和数据采集系统的便捷途径。使用它进行原理研究、设计、测试并实现仪器系统时,可以大大提高工作效率。

灰色理论是以复杂的数学理论为指导,在复杂的高等数学中推导得到的一种预测理论。要建立一个灰色模型,前提必须是了解并且懂得高等数学的人,还要有控制理论基础,加上预测理论等许多知识的集合才可以做到。LabVIEW的出现可以将问题简化,利用其强大的数据处理功能,建立一个可视化操作仪器,让灰色预测通俗化,使之不再是专业人员的专利[1]。

1灰色系统理论

1.1　GM(1,1)模型

GM(1,1)的意义:

G(grey)表示灰色,M(model)表示模型,第一个1表示一阶,第二个1表示一个变量。

GM(1,1)灰微分方程[2]:

(1)

1.2　GM(1,1)参数辨识算式

若有原始数

x(0)=(x(0)(1),x(0)(2),x(0)(3),…,x(0)(n))

其1-AGO生成数列:

x(1)=(x(1)(1),x(1)(2),x(1)(3),…,x(1)(n))

(2)

且x(1)与x(0)均满足灰微分方程条件,则x(0)与x(1)中各时刻数据时刻满足式中[2]:

z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)

k=2,3,4…n

(3)

(4)

GM (1,1)模型的离散响应方程:

(5)

(6)

1.3　可建模性检验

(7)

对于级比检验不合格的序列,必须做数据处理,使其变换后的序列,其级比满足式(8)。通常变换处理的途径为平移处理、对数处理、方根处理等。

1.4　模型精度检验

1.4.1残差检验

求残差及相对误差:

(8)

(9)

1.4.2后验差指标检验

计算标准差比:

(10)

其中：

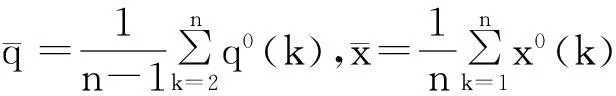
c是后验差检验的重要指标。指标c值越小越好,c值越小,说明S1越小,S2越大。S1小,说明残差数据方差小,或者说残差数据摆动幅度小,说明残差的离散程度小,S2越大,说明原始数据方差大,或者说原始数据摆动幅度大,说明原始数据规律性较差。c小,表明尽管原始数据很离散,而模型所得计算值与实际值之差并不离散。一个好的模型要求在S1小的前提下,S2尽可能的大。作为一个综合指标要求,c越小越好。一般要求c<0.35,最大不超过0.65[5]。如表1所示。

表1　精度检验等级

2LabVIEW应用实例

从以上理论推导过程,可以看出,计算过程繁杂,且有矩阵等数学运算,计算比较麻烦。本文提出的方法不可以解决此问题,而且将大大提高计算速度。LabVIEW[6]将数据处理等数学表达式做成了可供该软件环境下调用的模块,利用这些模块快速组建建模过程,得到估计参数,建立灰色模型,从而避免大量的数学计算和数学推导,简化计算过程。即将数学的推导过程用简单的程序流程图来实现,从而达到简化计算过程的目的。

已知一组测量结果如下,满足GM(1,1)模型选用条件如表2:

表2　实验数据

根据灰色系统理论的知识,首先进行合格性检验。编写对应程序如下:取出1个数组大小模块,2个数组子集模块,1个数组极大值极小值模块,根据公式(7),可编写求出输入数列的级比,并求出极大值和极小值程序框图。再由一个公式节点模块,写出数组的级比满足条件,若级比满足(7)式,则合格,指示灯亮。否则,不合格。该过程利用了一个Stacked Sequence structure结构。

其次,建模条件满足后,便可以进行灰色GM(1,1)模型的建立,该过程用了4个平铺顺序结构,完成后为了节省空间,转换成了堆叠顺序结构。首先根据灰色理论部分公式(2),写出累加计算程序,再根据公式(3),写出建立数组矩阵程序,接着根据公式(4),写出模型参数求解程序。

再次,根据以上模型参数建立GM(1,1)模型,根据公式(5)及公式(6),写出数据预测程序。

然后,再进行后验差的检验。从而为后面的数据精度等级的确定确立理论依据。根据公式(8)和公式(9),写出预测数据与历史数据的预测误差程序,这里的误差是指相对于历史数据的误差,即相对误差。再利用标准差模块,写出误差和历史数据的标准方差程序,根据公式(10)可完成后验差计算程序编写。

图1　程序流程图

最后,进行精度等级的评定。根据表1,将精度等级划分为4个等级,该过程利用了3个case循环结构,和后验差比值的局部变量,方法为在对应模块上右击,选择创建,找到局部变量模块单击即可,总共应用到了4个。再利用相关的布尔运算便可以完成。以上程序基本完成了灰色预测所需要的功能,总共用到的循环有三类:1个while循环,用来保持前面板的运行后状态,8个堆叠顺序结构,其中5个用来完成数组输入到后验差指标计算的功能,3个用来完成组织系统结构的功能,1个case结构,判断数据的合格性,如合格,进行相应的计算,否则,不计算,并弹出对话框,结束程序。程序框图按照所需的逻辑连接起来后,便可以实现一个完整的灰色预测过程。输入数据个数不限,均可以完成相应的功能。其完整连接后,程序如图1所示,前控制面板如图2所示。

图2　控制面板

从运行界面可以一目了然地看到各种指标性能,如预测输出、预测误差、模型参数、建模合格性、后验差比值、模型的精度等级。预测时,只要输入相应的历史数据,便可以在短短的几秒中实现,大大简化了计算过程,给计算带来了方便。

3结束语与展望

本文利用LabVIEW的数据处理功能,结合灰色理论,能根据少量测量数据快速建立测量过程控制模型,并得出预测数据。算例证明了本方法的实用性和有效性,具有一定的应用价值。目前程序可以完成对一位数组模型的建立,对于多维数组模型,原理上同样适用,还需要进一步研究。

(责任编辑吕春红)

参考文献：

[1].邓聚龙.灰色系统基本方法[M].武汉：华中理工大出版社，1987.

[2]陈松涛，张娟.灰色GM(1,1)模型在虚拟仪器测量控制过程中的应用[J]. 通讯与广播电视, 2005,(4).

[3]谭冠军，卜英勇.灰色GM (1,1)模型在可靠性工程中的应用研究[J]. 中南工业大学学报,1998.29 No(3):271-272

[4] 罗佑新，张龙庭，李敏.灰色系统理论及其在机械工程中的应用[M].长沙：国防科技大学出版社，2001.

[5] K. L. Wen, Grey systems: modeling and prediction[J]. Yang's Scientific Research Institute, AZ, USA, 2004.

[6]王磊,陶梅.精通 LabVIEW 8.0[M]. 北京:电子工业出版社,2007.

Applied Research of LabVIEW in Measurement of Gray Model GM (1,1)

LI Jin-yu

(Department of Automatic Control, Henan Mechanical and Electrical

Engineering College, Xinxiang 453000, China)

Abstract:The aim of this paper is by combing labview’s powerful data-processing functions and grey GM(1,1) model to design and develope a visual test platform,by which the complicated mathematical calculation process was insteaded by diagram of the process, greatly simplifying the calculation of time and providing a convenience for the project and non-engineering staff.The example shows that this method is simple and practical and has a high precision.

Key words: grey theory; data forecast; LabVIEW