Studies of Iron-Porphyrin Complexes with Different Axial Ligands by Both Spin-Restrict and Spin-Polarized Density Functional Reactivity Theory

-, -, -, ,

(School of Pharmacy, Hunan University of Chinese Medicine, Changsha 410208, China)



Studies of Iron-Porphyrin Complexes with Different Axial Ligands by Both Spin-Restrict and Spin-Polarized Density Functional Reactivity Theory

WUWen-jie,ZHANGXiao-qing,HUIHua-ying,LILong,HUANGYing

(School of Pharmacy, Hunan University of Chinese Medicine, Changsha 410208, China)

AbstractHeme is a key cofactor of hemoproteins in which porphyrin is often found to be preferentially metallated by an iron cation. Density functional reactivity theory (DFRT) descriptors and their spin-polarized version have been previously applied to understand the metal-binding specificity of porphyrin in the literature. It was found that the iron-porphyrin complex significantly differs in many aspects from porphyrin complexes with other metal cations. In this study, we employ DFRT and its spin-polarized version to investigate the reactivity for a series of small ligands axially bonded to the iron-porphyrin complex with the general formula of L-Fe(Ⅱ)-porphyrin, where L= SMe, SHMe, 1H-imidazole, imidazol-1-ide, OH, H2O, H2O2, CO, NO, O2, furan, isoindole, pyrrole, and pyridine. Both global and local DFRT descriptors were examined within this framework. We found that, from the analysis of DFRT and spin-polarized DFRT descriptors, CO is the ligand giving rise to the most stable Fe(Ⅱ)-prophyrin complex, which at the same time is less reactive than other systems. We also discovered substantial differences in structural and reactivity descriptors between the systems with L=H2O and SHMe systems as well as the systems with L=OH and SMe. Quantitative reactivity relationships have been revealed. These results should help better understanding of the reactivity of heme bonding with different ligands for heme-containing enzymes and other metalloproteins alike.

Key wordsporphyrin; heme; density functional reactivity theory (DFRT); spin-polarized DFRT

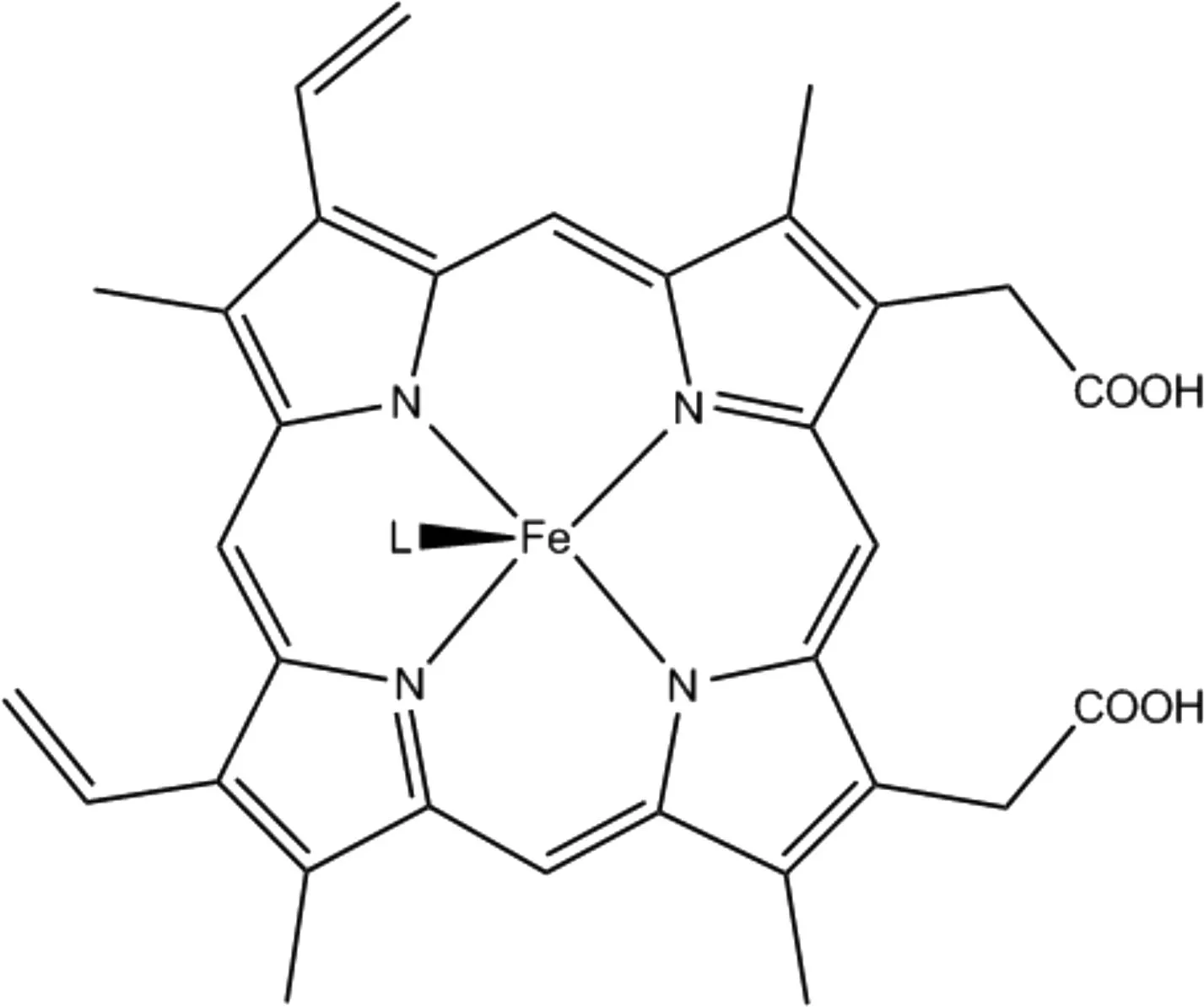
Scheme 1　L-Fe(Ⅱ)-porphyrin systems investigated in this work, with L can be replaced by fractional groups in amino acid that usually bonded with heme in nature: from cysteine: MeS-, SHMe, from histidine: 1H-imidazole, imidazol-1-ide, from water: O2-, HO-, H2O, H2O2, and small gaseous molecules: CO, NO, O2, and also some other common ligands: furan, isoindole, pyrrole, pyridine

Heme is a metal-binding porphyrin consisting of a heterocyclic organic ring made from four pyrrole subunits linked via methine bridges (Scheme 1). As the core cofactor of hemoproteins, it serves as a prosthetic group for many biological processes including oxidative metabolism[1-3], xenobiotic detoxification, synthesizing and sensing of diatomic gases, cellular differentiation, gene regulation at the level of transcription, protein translation and targeting, and protein stability. Therefore, hemoproteins such as hemoglobin[4], myoglobin[5], hemocyanin[6-7]and neuroglobin[8]are abundance in nature and play essential roles in physiological processes as sensors, activators, and carriers of gaseous molecules. Hemoglobin is most commonly found in its oxygen-binding state where the bonded metal cation is a divalent iron, Fe(Ⅱ). When in its resting or functioning state, up to two axial ligands are required to bond with the metal cation in the metal-porphyrin complex to carry out the catalytic process. The most common axial residues in hemoproteins are histidine and cysteine.

Density functional reactivity theory (DFRT) and spin-polarized DFRT (SP-DFRT) have recently been applied to understand the metal-binding specificity of porphyrin[1-2], where it was found that both structure and electronic properties of the metal cation play important roles in differentiating its metal-binding specificity. Differences in metal-binding specificity of metal-porphyrin complexes can result from different causes. For example, no Ca-porphyrin or Cd-porphyrin complex exists in nature because Ca(Ⅱ) and Cd(Ⅱ) cations are too big to fit into the inner cavity of the porphyrin ring. For other complexes such as Zn(Ⅱ) and Mn(Ⅱ), it was concluded that electronic properties, as shown from the second-order perturbation theory analysis of the Fock matrix in the NBO basis and chemical reactivity descriptors such as hardness, electrophilicity, and dual descriptors, dictate their metal-binding specificity. It has also been revealed that the iron complex differs from other metal ion complexes in bonding and reactivity properties (i.e. charge distribution, stability, and nucleophilicity) when two axial bonds are formed, enhancing and facilitating the role of the iron cation as the center of the catalytic process and thus implying that the number and nature of the axial ligands also play an important role in the catalytic process. Another conclusion from those previous studies in the literature is that Fe(Ⅱ) and Ru(Ⅱ) complexes show similar reactivity from the spin unresolved DFRT perspective, but from the spin-polarized version of DFRT, the Fe-porphyrin complex stands up and often possesses the smallest value for each of the SP-DFRT quantities in most cases, indicating that the Fe system is most likely to increase the total spin number, and the spin resolution showed a remarkable difference between Ru and Fe complexes. These results suggest that the specificity difference of porphyrin between Fe and Ru cations is originated from both the electron and spin properties and that to differentiate their behaviors one has to resort to spin resolved reactivity indices.

What is missing in these studies is that the impact of axial ligands is not well understood. These ligands might well affect the metal-porphyrin’s reactivity and metal-binding specificity. In this study, we will work on this missing piece of the puzzle and investigate thoroughly. We will try to address the following question: From the perspective of DFRT and SP-DFRT, in the gas phase under vacuum, what are the main differences in structure and reactivity properties for the iron-porphyrin complex when different axial ligands are present?

1Theoretical Background and Computational Details

These following systems with the general formula of porphyrin-Fe(Ⅱ)-L will be investigated in this study, where the ligand L represents either the fractional group in amino acid that usually bonds with heme in nature, such as cysteine, which is simplified by-SMe and SHMe, or histidine, which is represented by 1H-imidazole and imidazol-1-ide, or from water related species like O2-, HO-, H2O, and H2O2, or other small gaseous molecules, such as CO, NO, and O2. We also considered some other commonly available ligands, e.g., furan, isoindole, pyrrole, and pyridine. To study the impact of the axial ligands on structural and electronic properties of these complex, we used the divalent Fe(Ⅱ) as the core metal cation.

In DFRT[9], also called conceptual DFT or chemical DFT, many global and local reactivity descriptors have been introduced and applied to a number of problems[1-2,10-15]. In this paper, the descriptors we mainly employed are the following. Chemical potential,μ, and global hardness[16-17],η, are defined as the following derivatives:μ=(∂E/∂N)V=-χandη=(∂2E)/∂N2)V= (∂μ/∂N)V, respectively, whereEis the total energy of the system,Nthe number of electrons,νthe external potential, andχelectronegativity. According to Mulliken[18],

μ=-χ= -(I+A)/2,

(1)

η=I-A,

(2)

withIandAas the first ionization energy and electron affinity, respectively, which can be approximated by the HOMO and LUMO energies viaI≈-εHOMOandA≈-εLUMO[19]. Softness[20],S, is defined as the inverse of the hardness,

S= 1/2η,

(3)

and the electrophilicity index[21], a measure of the lowering of the total binding energy due to the maximal electron acceptance, can be expressed in terms ofμandηas

ω=μ2/2η.

(4)

Other global DFRT reactivity indices such as nucleofugality, ΔEn, and electrofugality, ΔEe, are defined as follows[22-23]:

ΔEn≡ -A + ω = [(μ + η)2]/(2η),

(5)

ΔEe= I + ω = [(μ - η)2]/(2η).

(6)

These global reactivity descriptors from the DFRT framework,μ,η,ω, ΔEn, and ΔEe, will be used to appraise the global chemical reactivity of our systems.

To describe regioselectivity tendencies of individual atoms in molecules, local DFRT descriptors were employed. The first well known example of such a category is called the Fukui function[24-25], defined asf(r) = (∂ρ(r)/∂N)V= (∂μ/∂v(r))N, whereρ(r) is the electron density. Yang and Mortier[26]have proposed that for systems with a gain of electrons the condensed Fukui index,

fk+= qk(N + 1) - qk(N),

(7)

in the finite difference approximation is a measure of nucleophilic attack, whereqk(N) is the gross atomic charge for atomkwithNelectrons, obtained from a population analysis (such as NBO analysis). For systems that can donate electrons, the condensed Fukui index is susceptible to electrophilic attack with

fk-= qk(N) - qk(N -1).

(8)

For radical attack reactions,

fk0= (fk++ fk-)/2,

(9)

whereqk(N + 1), qk(N), andqk(N - 1) are the gross NBO population on atomkin a molecule withN+1 (anion state),N(neutral state), andN-1 (cation state) electrons, respectively.

In spin-polarized DFRT[27-29], the spin potential,μS, is defined as:μS=(∂E/∂NS)v,B,Nand can be further approximated by

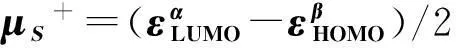
(10)

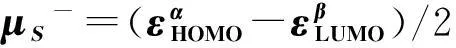
(11)

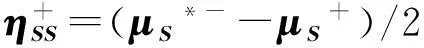
(12)

ωS±=-(μS±)2/(2ηSS).

(13)

Spin-polarized Fukui function[30]is defined asfSS(r)=(∂ρS(r)/∂NS)V,B,N, andfNS(r)=(∂ρ(r)/∂NS)V,B,N, whereρS(r) is spin density. Under the frozen core approximation,fSS,k±andfNS,k±can be obtained as follows:

fSS,k+=(|ΦLUMO, α,k|2+|ΦHOMO, β,k|2)/2,

(14)

fSS,k-=(|ΦHOMO, α,k|2+|ΦLUMO, β,k|2)/2,

(15)

fNS,k+=(|ΦLUMO, α,k|2-|ΦHOMO, β,k|2)/2,

(16)

fNS,k-=(|ΦHOMO, α,k|2-|ΦLUMO, β,k|2)/2,

(17)

whereΦHOMO,α,k,ΦHOMO,β,k,ΦLUMO,α,k,ΦLUMO,β,kare HOMO and LUMO orbitals forαandβelectrons, respectively.

In addition to the global and local descriptors from DFRT and SP-DFRT, we will also employ NBO analyses to perform second-order perturbation analyses to understand the bonding features between the metal cation and the porphyrin ring and between the metal cation and the axially bonded pyridine groups.

All calculations were performed using the B3LYP functional and a compound basis set, where the 6-31G basis sets were used for the elements C and H, and Pople’s 6-311+G(d) basis sets were used for N, O, S and Fe. All calculations were performed using the Gaussian 09 package version D01[31].

2Results and Discussion

Tab.1 shows a few key structural parameters of the series of L-Fe-porphyrin complexes with varying ligands L. Also shown in the Table is the multiplicity of the lowest-energy spin state for each of the systems studied. One can see that for the majority of complexes, the bond length between Fe-ion and coordinating atom of the ligand, Fe-LA, in the systems where the coordinating atom is protonated, is longer than that of the system whose coordinating atom is deprotonated. For example, Fe-LA of HO--Fe(Ⅱ)-porphyrin is 1.919 Å, whereas the same bond length becomes 2.254 Å in H2O-Fe(Ⅱ)-porphyrin. In MeS-Fe(Ⅱ)-porphyrin, the Fe-LA bond is 2.398 Å, but it becomes 3.001Å in MeHS-Fe(Ⅱ)-porphyrin. This is reasonable because the negatively charged ligands are more strongly interacting with the positively charged iron cation. Also, the corresponding bond length between Fe ion and porphyrin plane, Fe-plane, has a reverse tendency, that is, the Fe-plane distance is shorter if the coordinating atom is protonized. For example, Fe-plane of HO--Fe(Ⅱ)-porphyrin is 0.665 Å, while Fe-plane of H2O-Fe(Ⅱ)-porphyrin is 0.155 Å. The Fe-plane distance of MeS--Fe(Ⅱ)-porphyrin is 0.625 Å, whereas that of MeHS-Fe(Ⅱ)-porphyrin is 0.081 Å. This tendency, shown clearly in Fig.1, is resulted from the stronger Fe-OH-or Fe-S-interaction in the deprotonated case: Since more interactions are devoted to this bond, fewer interactions from Fe to other species are subsequently resulted. For the majority of complexes the bond length between Fe-ion and porphyrin nitrogen atom, Fe-N(Pph) are rather similar, around 2.1 Å.

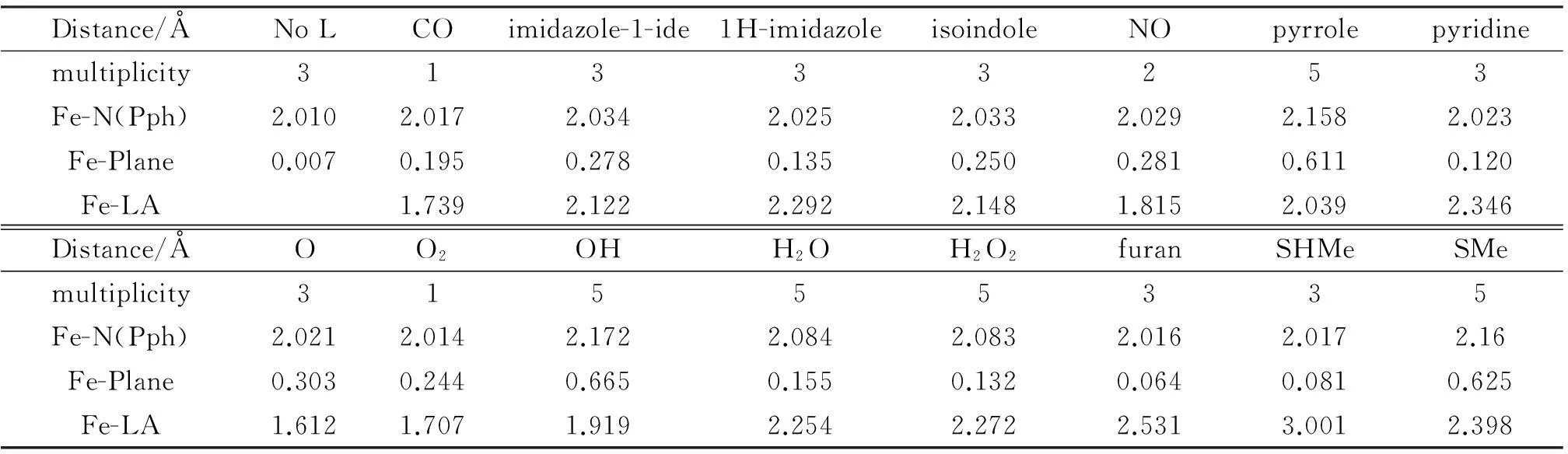
Tab.1　Selected structural parameters from the optimized structure of the heme complexes with 14 different ligands*

*“Fe-N(Pph)” stands for the average bond length of Fe ion-porphyrin nitrogen bond distance; “Fe-Plane” denotes the out-of-plane distance of the metal ion from the porphyrin plane; “Fe-LA” represents the bond length of the Fe ion-coordinating atom bond.

From the structural results, one finds that the values of Fe-N(Pph) and Fe-plane in MeS--Fe(Ⅱ)-porphyrin, 2.16 Å and 0.625 Å, respectively, are largest among the series, while in MeSH-Fe(Ⅱ)-porphyrin, Fe-N(Pph) and Fe-plane distances are the shortest (2.017 Å and 0.081 Å, respectively). This difference, especially in the value of Fe-plane distance of 0.625 Å -0.081 Å =0.544 Å, indicates that the flexibility of the porphyrin ring, which governs the resonance of electrons on the plane, can be affected by the pronated or deprotonated state of the axial sulfur atom. The same effect is observed in the systems with L=H2O and HO-, where the difference of 0.665 Å-0.155 Å=0.510 Å in the Fe-plane distance is seen. From these results, one can see that whether or not the axial ligand is deprotonated affects the extent of resonance on the heme plane and thus its chemical reactivity. Also, we find that in the system in which the coordinating atom is either S or O, the changing between protonation and deprotonation affects more than that in the remaining systems. Such changing, especially when the coordinating atom is oxygen, can be relatively easily occurred in nature. This might be the precise reason why the heme systems in nature prefer to choose S or O atom as the binding atom in the axial ligand.

(a) H2O-Fe(Ⅱ)-porphyrin　　　　　　　　　　　　　　　　(b) HO-Fe(Ⅱ)-porphyrin

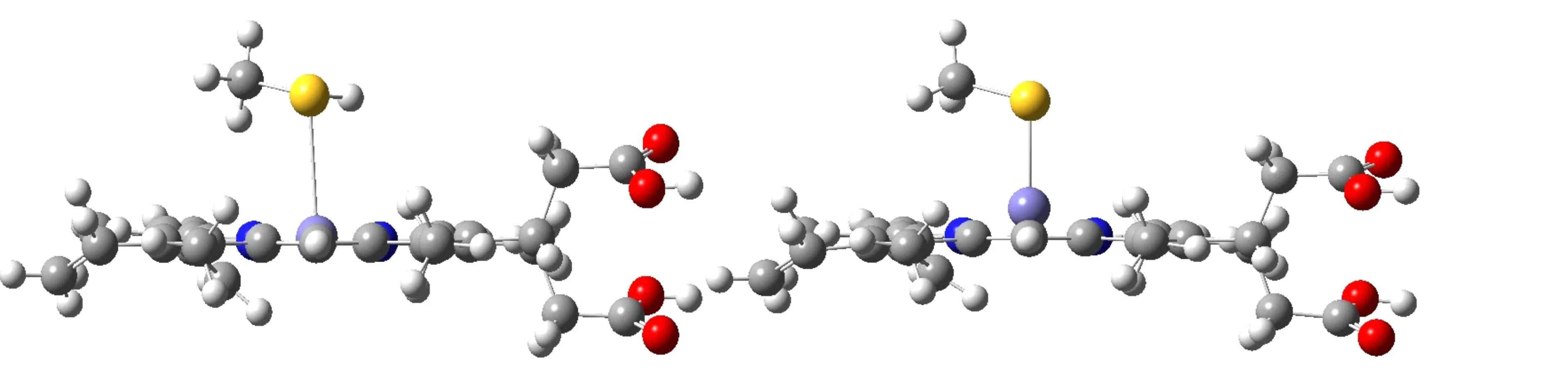
(c) MeHS-Fe(Ⅱ)-porphyrin　　　　　　　　　　　　　　　　(d) MeS-Fe(Ⅱ)-porphyrinFig.1　Comparison of the optimized structures between the systems that the coordinating atom is more saturated: (a) H2O-Fe(Ⅱ)-porphyrin, (c) MeHS-Fe(Ⅱ)-porphyrin and the systems that the coordinating atom is less saturated: (b) HO-Fe(Ⅱ)-porphyrin, (d) MeS-Fe(Ⅱ)-porphyrin

From the information of NBO charge distribution shown in Tab.2, one finds that in the systems with L=H2O2, H2O, HO-, the decline of electron density on Fe(Ⅱ) cation caused by coordination—the difference in electron density on Fe-ion between Fe(Ⅱ)-porphyrin and L-Fe(Ⅱ)-porphyrin—is larger than that in other systems. This large reduction of charge on the heme reaction center might well be a prerequisite of the catalyst. Also, compared with the most negative coordinating atom in those systems, they have the most ionic bond between the coordinating atom and Fe-ion. Comparatively, Fe-LA in the systems with L=CO and NO are more covalent bonding, especially OC-Fe(Ⅱ)-porphyrin, which has the lowest charge value on Fe ion, 0.677. From Tab.2, the donor-acceptor back-bonding interactions for pairs such as porphyrin (donor) → Fe (acceptor), Fe (donor) → porphyrin (acceptor), etc., from the second-order perturbation theory analysis of the Fock matrix in the NBO basis, provide the hyperconjugation or back-bonding interaction energies between different chemical motifs in a complex. From this Table, O2-Fe(Ⅱ)-porphyrin has larger value on L→Fe and Fe→Pph. That is, the back-bonding interactions where ligand acts as a donor and Fe as the acceptor, and where Fe as a donor and porphyrin as the acceptor, are stronger than most of other systems in the series. Data of bond length information from Tab.1 also shows that Fe-LA of O2-Fe(Ⅱ)-porphyrin is shorter than the rest. Therefore, O2is most strongly stabilized by porphyrin where Fe-ion acts as a “duct”. On the contrary, OC-Fe(Ⅱ)-porphyrin has larger value on Pph→Fe and Fe→L. In this system, the effect of hyperconjugation is quite different from that of the system with L=O2. This result can be used to explain why CO acts as catalyst killer, where electrons move away from porphyrin plane to C=O by hyperconjugation in OC-Fe(Ⅱ)-porphyrin to form a more stable bond, unlike O2-Fe(Ⅱ)-porphyrin, where electrons are tending to be delocalized on the heme plane, resulted in the fact that the system becomes more reactive.

Global descriptor results from DFRT including HOMO/LUMO, chemical potential, hardness, and electrophilicity index for the three classes of metal-porphyrin complexes are tabulated in Tab.3. Since hardness is an indication of molecular stability, the smaller the hardness the less stable the system becomes; one finds that OC-Fe(Ⅱ)-porphyrin has the highest value of chemical hardness, indicating that it is much more stable than any other systems in the series. These two phenomena may be the reasons why CO acts as a catalyst killer. On the contrary, the systems with L=HO-, SMe, O2, have smaller values of hardness, indicating that these compounds are more likely to be intermediaries in chemical reactions, or that they are unstable and the ligand can be easily released under certain circumstances, like the system with L=O2.

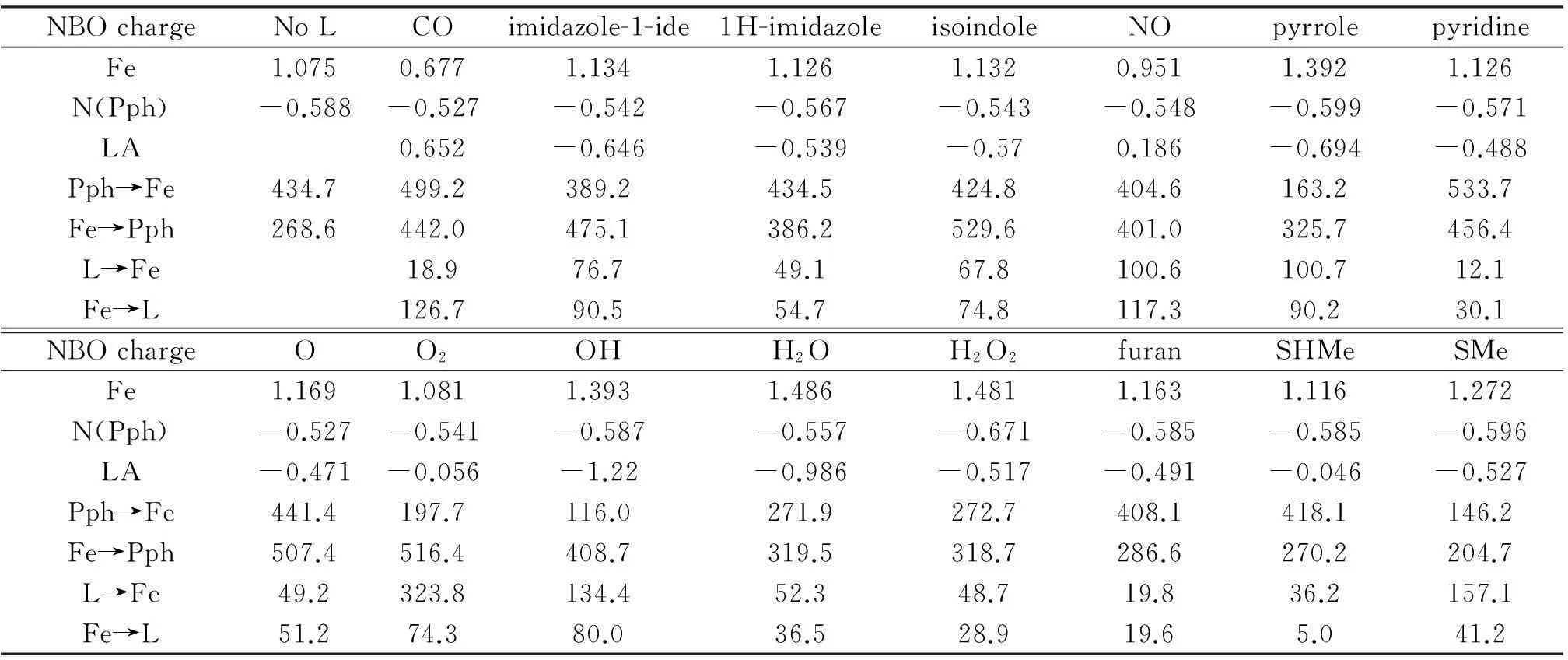
Tab.2　NBO charge distribution and second-order perturbation theory analyses of the heme complexes with 14 different ligands*

*Charges listed are those on the Fe-ion, and nitrogen atoms of porphyrin, N(Pph), and coordinating atom, LA. L→Fe stands for the donor-acceptor interaction between L (ligand) and Fe-ion, where L serves as the electron donor and Fe as the electron acceptor. The total interaction, in kcal/mol, is the sum of all orbital contributions larger than 0.05 kcal/mol.

Tab.3　Global reactivity descriptors from conceptual DFT including frontier orbitals HOMO and LUMO, chemical potential μ,

Tab.4　Calculated DFT-based spin Global Reactivity Indicators (Units in eV)

Tab.5 shows local reactivity descriptors from DFRT for a few key atomic sites of the systems. Recall that the dual descriptorf(2)(r) is defined as the difference between the nucleophilic Fukui function,f+(r), and the electrophilic Fukui function,f-(r), under the finite difference approximation and that it is positive in electrophilic (electron-accepting) regions and negative in nucleophilic (electron-donating) regions[1,32-33]. From Tab.5, one finds that the system with L=CO has the smallest values of Fukui function: bothfFe+(0.002) andfFe-(0.003), indicating that OC-Fe(Ⅱ)-porphyrin is unlikely to obtain or donate electrons especially on Fe-ion. Considering with global descriptors of OC-Fe(Ⅱ)-porphyrin, which also show a stable and inactive nature, one finds that after the coordination with CO, the reactivity of heme is completely destroyed.

3Conclusions

Porphyrin metallated with a divalent metal cation, mostly Fe (Ⅱ) in nature, is one of the key cofactors in hemoproteins. Recent studies have utilized density functional reactivity theory and its spin-polarized version to explain the nature of metal-binding specificity. In this contribution, we also employed DFRT and SP-DFRT to investigate the structure and both global and local reactivity descriptors of a series of L-Fe(Ⅱ)-porphyrin complexes with L = CO, imidazole-1-ide, 1H-imidazole, isoindole, NO, pyrrole, pyridine, O2-, O2, HO-, H2O, H2O2, furan, SHMe, MeS-to study the impact of axial ligands on the structure and reactivity propertie of the heme systems. We found that OC-Fe(Ⅱ)-heme has the most stable and inactive system, serving as a catalyst killer. We also discovered substantial differences in structural and reactivity descriptors between the systems with L=H2O and SHMe systems as well as the systems with L=HO and SMe. Quantitative reactivity relationships have been revealed. These results should help better understanding of the reactivity of heme bonding with different ligands for heme-containing enzymes and other metalloproteins alike.

References:

[1]FENG X T, YU J G, LEI M,etal. Toward understanding metal-binding specificity of porphyrin: A conceptual density functional theory study [J]. J Phys Chem B, 2009,113(40):13381-13389.

[2]FENG X T, YU J G, LIU R Z,etal. Why iron? A spin-polarized conceptual density functional theory study on metal-binding specificity of porphyrin [J]. J Phys Chem A, 2010,114(21):6342-6349.

[3]SONO M, ROACH M P, COULTER E D,etal. Heme-containing oxygenases [J]. Chem Rev, 1996,96(7):2841-2888.

[4]MONOD J, WYMAN J, CHANGEUX J P. On the nature of allosteric transitions: a plausible model [J]. J Mol Biol, 1965,12(1):88-118.

[5]QIU Y, SUTTON L, RIGGS A F. Identification of myoglobin in human smooth muscle [J]. J Biol Chem, 1998,273(36):23426-23432.

[6]WILCOX D E, PORRAS A G, HWANG Y T,etal. Substrate analog binding to the coupled binuclear copper active site in tyrosinase [J]. J Am Chem Soc, 1985,107(13):4015-4027.

[7]WINKLER M E, LERCH K, SOLOMON E I,etal. Competitive inhibitor binding to the binuclear copper active site in tyrosinase [J]. J Am Chem Soc, 1981,1039(23):7001-7003.

[8]BURMESTER T, WEICH B, REINHARDT S,etal. A vertebrate globin expressed in the brain [J]. Nature, 2000,407(6803):520-523.

[9]LIU S B, PARR R G. Second-order density-functional description of molecules and chemical changes [J]. J Chem Phys, 1997,106(13):5578-5586.

[10]HUANG Y, ZHONG A G, RONG C Y,etal. Structure, spectroscopy, and reactivity properties of porphyrin pincers: A conceptual density functional theory and time-dependent density functional theory study [J]. J Phys Chem A, 2008,112(2):305-311.

[11]ZHONG A G, RONG C Y, LIU S B. Structural and dynamic properties of (SiO2)6silica nanostructures: a quantum molecular dynamics study [J]. J Phys Chem A, 2007,111(16):3132-3136.

[12]LIU S B. Origin and nature of bond rotation barriers: a unified view [J]. J Phys Chem A, 2013,117(5):962-965.

[13]LIU S B, GOVIND N, PEDERSEN L G. Exploring the origin of the internal rotational barrier for molecul es with one rotatable dihedral angle [J]. J Chem Phys, 2008,129:094104.

[14]XIA Y, YIN D L, RONG C Y,etal. Impact of lewis acids on diels-alder reaction reactivity: A conceptual density functional theory study [J]. J Phys Chem A, 2008,112(40):9970-9977.

[15]LIU S B. Where does the electron go? The nature of ortho/para and meta group directing in electrophilic aromatic substitution [J]. J Chem Phys, 2014,141(19):194109.

[16]PEARSON R G. Hard and soft acids and bases [J]. J Am Chem Soc, 1963,85(22):3533-3539.

[17]PARR R G, PEARSON R G. Absolute hardness: companion parameter to absolute electronegativity [J]. J Am Chem Soc, 1983,105(26):7512-7516.

[18]MULLIKEN R S. A new electroaffinity scale; together with data on valence states and on valence ionization potentials and electron affinities [J]. J Chem Phys, 1934,2(11):782-793.

[19]JANAK J F. Proof that ∂E/∂ni=ε in density-functional theory [J]. Phys Rev B, 1978,18(12):7165-7168.

[20]YANG W, PARR R G. Hardness, softness, and the fukui function in the electronic theory of metals and catalysis [J]. Proc Natl Acad Sci, 1985,82(20):6723-6726.

[22]AYERS P W, ANDERSON J S M, RODRIGUEZ J I,etal. Indices for predicting the quality of leaving groups [J]. Phys Chem Chem Phys, 2005,7(9):1918-1925.

[23]AYERS P W, ANDERSON J S M, BARTOLOTTI L J. Perturbative perspectives on the chemical reaction prediction problem [J]. Int J Quantum Chem, 2005,101(5):520-534.

[24]PARR R G, YANG W. Density functional approach to the frontier-electron theory of chemical reactivity [J]. J Am Chem Soc, 1984,106(14):4049-4050.

[25]LIU S B. Conceptual density functional theory and some recent developments [J] Acta Phys Chim Sin, 2009,25(3):590-600.

[26]YANG W, MORTIER W J. The use of global and local molecular parameters for the analysis of the gas-phase basicity of amines [J]. J Am Chem Soc, 1986,108(19):5708-5711.

[27]VON BART U, HEDIN L. A local exchange-correlation potential for the spin polarized case: I [J]. J Phys C: Solid State Phys, 1972,5(5):1629-1642.

[28]RAJAGOPAL A K, CALLAWAY J. Inhomogeneous Electron Gas [J]. Phys Rev B, 1973,7(5):1912-1919.

[29]GUNNARSON O, LUNDQVIST B I. Exchange and correlation in atoms, molecules, and solids by the spin-density-functional formalism [J]. Phys Rev B, 1976,13(10):4274-4298.

[31]FRISCH M J, TRUCKS G W, SCHLEGEL H B,etal. Gaussian 03, Revision E.01[CP]. Gaussian, Inc: Wallingford CT, 2014.

[32]MORELL C, GRAND A, TORO-LABBE A. New dual descriptor for chemical reactivity [J]. J Phys Chem A, 2005,109(1):205-212.

[33]AYERS P W, MORELL C, DE PROFT D,etal. Understanding the woodward-hoffmann rules by using changes in electron density [J]. Chem Eur J, 2007,13(29): 8240-8247.

(编辑杨春明)

连接不同轴向配体铁卟啉体系的自旋非极化和自旋极化密度泛函活性理论研究

吴文杰，张晓青，惠华英，李龙，黄莺*

(湖南中医药大学药学院, 中国 长沙410208)

摘要血红素在许多生化反应中起着至关重要的作用,且血红素的核心为卟啉环配位铁离子．文献采用密度泛函活性理论及其自旋极化方法对卟啉环连接的金属离子的选择性进行了研究，发现卟啉环连接铁离子时其结构和活性与连接其他金属离子的体系有很大的差异．实验研究表明，轴向连接不同配体对体系的结构和活性有显著影响．本文采用密度泛函活性理论及其自旋极化方法对铁卟啉体系中铁离子轴向连接不同配体的体系进行系统探究．轴向配体包括 SMe, SHMe, 1H-咪唑及衍生物, OH, H2O, H2O2, CO, NO, O2, 呋喃，异吲哚，吡咯和吡啶．通过对全局和局域化学活性描述符的计算分析发现，当配体是CO时，体系化学性质稳定、反应活性也低；在众多种体系中H2O和SHMe的得失质子对体系活性的影响最大．这些计算结果对更深入了解血红素及其类似体系的活性和作用机理有重要意义．

关键词卟啉环; 血红素; 密度泛函活性理论; 自旋-密度泛函活性理论

中图分类号O621.13

文献标识码A

文章编号1000-2537(2015)05-0040-08

通讯作者*,E-mail：1125218638@qq.com

基金项目：湖南省教育厅科研资助项目(14C0806)

收稿日期：2015-01-28

DOI:10.7612/j.issn.1000-2537.2015.05.007