一种快速准确的图像配准算法

靳 峰,冯大政

(1.西安电子科技大学计算机学院,陕西西安 710071；2.西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)

一种快速准确的图像配准算法

靳 峰1,2,冯大政2

(1.西安电子科技大学计算机学院,陕西西安 710071；2.西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)

通过对图像配准目标函数的分析,提出了一种结合相似性和空间序列特征的配准算法.图像配准的目标函数包含两个最优解,一个是最大数量的有效特征点,一个是最高精度的图像变换矩阵,这两个部分可以使用不同的特征点匹配矩阵来求解.其中,使用基于相似性的中心对称局部二值模式描述子获得变换矩阵,使用基于空间序列特征的统计偏转角度序列描述子获取有效特征点.后者是一种融合了局部结构特征和全局统计特性的描述子,具有结构简单、描述准确的优点.实验结果表明,将两种描述方法相结合进行图像配准,具有配准精度高和运算时间短的优点.

图像配准;特征点匹配;描述子;中心对称局部二值模式;空间序列特征

图像配准是影像处理和分析的一个最重要步骤.一直以来,图像配准都是计算机视觉、模式识别、医学图像处理和遥感领域的热点.目前应用最广泛的是基于特征点的配准方法[1-4].该方法通过特征检测提取图像中的特征点,利用特征点的匹配关系建立图像之间的配准映射变换,实现图像配准.

一些常见的配准算法基于特征点的相似性进行点的比对和匹配,进而实现图像的配准.该类算法为了提高特征点的精确性和惟一性,往往使用多维向量来描述特征点.例如,著名的尺度不变特征变换（Scale Invariant Feature Transform,SIFT)算法采用128维向量描述特征点.一般来讲,向量维数越高,特征点描述越精确,运算的复杂程度就越高.

近年来,一种基于特定点间的约束关系的配准方法越来越受到研究者的重视.该类方法在光学图像或遥感图像的配准、图像分类、模式与目标识别以及三维重构等领域获得了许多的应用[5-8].文献[5]提出了一种基于最近邻图形结构的图配准算法,使用最近邻约束策略构造待配准特征的局部邻近结构作为特征描述方法.文献[6]提出了名为受限空间序列约束的特征点配准算法,同样使用最近邻约束策略,选取待配准点附近若干最近邻点与待配准点间的夹角序列作为特征点的描述方法.该类方法最显著的特点是利用空间上的约束关系来对特征点进行描述和匹配,对图像本身的信息依赖度低,也不需要对特征点进行复杂的描述.但是,其缺点在于该类算法对于特征点的描述是基于点与点之间的距离、角度或者序列,外点的存在会大大影响这种描述方法的精度,匹配算法往往就变成了剔除外点、求解最优匹配矩阵的优化算法.

经过对以上各种特征点描述和匹配方法的对比与分析,笔者提出了一个结合两种不同描述子的特征点匹配方法.采用两种不同的特征点描述子完成图像配准,一种是中心对称局部二值模式描述子（Center Symmetric Local Binary Pattern,CS-LBP),一种是下面定义的统计偏转角度序列描述子（Statistical Deflection Angle Order,SDAO).笔者提出的配准算法和特征点描述子克服了传统算法的缺点,降低了复杂的特征点描述对匹配过程的影响,也能对外点进行有效的剔除,是一种快速准确的配准算法.

1 图像配准目标函数

无论是基于相似性的图像配准算法,还是基于空间关系的方法,其特征点的匹配矩阵都可记为

其中,Λij是一个M×N的二维矩阵,M和N分别为待配准图像中的特征点数量,fij表示两幅图像中的一对特征点.

定义图像配准的一般目标函数为

其中,m为Λ中的匹配点对数量,Γ为图像变换矩阵.特征点的匹配目标实际上就是获得最大数量的匹配点对m和最高精度的图像变换矩阵Γs.对于目标函数的两个最优解m和Γs,可以使用两种不同的特征点描述方式进行求解.

新的目标函数定义为

其中,E为基于相似性的特征点匹配矩阵,D为基于空间序列的特征点匹配矩阵.使用矩阵E进行图像变换矩阵估计,求得Γs;使用矩阵D得到最大的有效特征点对.

基于相似性的特征点描述往往结构非常复杂,对于大量的点匹配操作效率不高;基于空间序列的特征点描述会受到外点的干扰,精度不够.可将两种方法相结合得到更好的配准效果.在基于相似性的图像配准过程中,特征点描述的优点之一就是独立性,外点的存在对于特征点的描述没有影响.因此,只需要少量特征点就可以进行图像变换矩阵估计.在著名的随机采样一致性算法中,3对不共线特征点就可以得到图像变换矩阵.在得到图像变换矩阵之后,可以利用Γ进行外点的删除,进而使用基于空间序列的匹配方法获得更多的匹配点对.其具体过程为:①利用若干不共线特征点的相似性描述估计图像变换矩阵Γ.②利用Γ进行外点删除;利用特征点的空间序列描述计算D,匹配点对数量记为t.若t＜Tf,Tf为指定常数,返回①;若t≥Tf,利用D求解Γ,同时若t＞m,m=t,返回②.④迭代运行以上步骤,直到m值稳定不变,或者迭代次数达到上限λ;使用最大的m计算Γs.

Tf是有效匹配点对数量的下限.当Tf足够小时,该算法对于外点容错的程度相当于目前鲁棒性最好的RANSC算法;但是,当Tf减小时,求解变换参数矩阵的运算量会大大增加,运算时间与M/t的3次方成正比.在迭代过程中,步骤③总是使用当前最优的内点集合求解Γ,但是步骤②使用全局特征点计算D来防止过收敛,最终得到的是最大内点集合的最优Γs.

2 图像配准

2.1 基于相似性的特征点匹配

局部二值模式（Local Binary Pattern,LBP)是目前对二维图像最有效的纹理分析特征之一[9].文献[10]首次将其应用到图像特征点描述,提出了中心对称局部二值模式（Center Symmetric LBP,CS-LBP)描述子.已有的实验结果表明,CS-LBP描述子在图像匹配方面比SIFT描述子具有更好的性能,且在存储空间需求和计算开销方面具有明显的优势.CS-LBP描述子的定义如下:

其中,ni和ni+P/2表示等间隔地分布在以（u,v)为圆心、R为半径的圆上的P个临近点中,关于中心点对称的两个像素点的灰度值;Tp为阈值.由式（4)可以看出,关于中心像素点对称的两个邻域点灰度值的差值被表示为一个P/2比特的二进制数,会得到2P/2种不同的模式.统计每一种模式出现的次数,就可以得到CS-LBP描述子.

CS-LBP描述子的缺陷在于其忽略了中心像素对局部纹理特征的影响,从而造成了局部纹理信息的丢失,即它在某些情况下无法得到足够的有效特征点.笔者提出了一种基于空间序列特征的描述子与其结合使用,再通过对匹配算法的改进弥补了这个不足.

2.2 基于空间序列特征的特征点描述子

基于空间序列特征的描述方法的基本思想是:图像中的特征点都可以视为一个图中相互连接的节点,每一个节点都可以被邻近节点所构成的局部区域所描述.笔者提出的一种基于局部结构特征的特征点描述子,将点C描述为

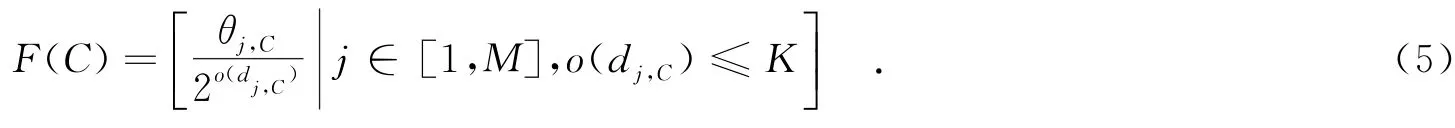
点C周围的特征点Lj,以θj,C为权值,按照dj,C的大小排成序列,构成对点C的描述.其中M为图像中特征点的个数;dj,C为特征点Lj到点C的距离;o（·)为序列函数,它表示特征点Lj到点C距离的位置关系,其取值为{1,2,…,K},K表示取点C周围邻近特征点的个数.例如,当K=7时,特征点Lj到点C的距离按照从小到大排列的序列为[3,6,5,2,4,7,1],o（d3,C)=1,o（d6,C)=2,以此类推.θj,C为特征点Lj到点C的连接权值,定义为特征点Lj经过全局参照点O到达点C所构成的夹角.点O为特定的样本空间的均值,称θj,C为统计偏转角度（Statistical Deflection Angle,SDA).统计偏转角度按照o（dj,C)构成的序列称为统计偏转角度序列（Statistical Deflection Angle Order,SDAO).

F（C)是一个空间序列描述子,它既包含点C周围特征点的局部结构,又包含特征点样本空间的全局信息.与传统的基于局部结构特征的特征点描述方法相比,笔者定义的空间序列描述子对特征点的局部结构特征进行了更加严格的约束.由于引入了全局参照点,避免了局部结构相似引起的描述混乱.

2.3 全局参照点

基于空间序列的特征点描述方式容易受到外点的干扰,SDAO描述子引入了全局参照点,该点的选取是否受外点影响对于SDAO描述子的精度尤为重要.笔者给出的算法可以有效地解决这一问题.在上述的配准过程中,步骤②进行了外点删除,称此刻剩余的点为“粗内点”.粗内点是由基于相似性的特征点匹配得到的,有效地避免了外点的干扰.将粗内点视为点样本空间,取其均值作为全局参照点O的定位.

图1显示了在初始外点比例为43%的情况下,粗内点在迭代过程中不断向最优内点集合逼近而得到的匹配精度.图中的横坐标为外点剔除操作的迭代次数,纵坐标为像素误差.随着外点的剔除,粗内点的匹配精度逐渐提高,代表了全局参照点的精度提高.

图1 全局参照点精度

3 实验与分析

3.1 有效性检验

为了检验特征点匹配的有效性,采用复现率作为衡量准则.此处的复现率是指:若在两幅图像中分别有r1和r2个特征点在变换后的图像中存在匹配点,而在两幅图像中实际检测到的对应匹配点对的数目为r3,则复现率R1=2r3/（r1+r2).

将图像处理中常用的“Lena”图像分别进行尺度和旋转变化下的图像配准,验证笔者提出的算法在图像配准一般应用上的有效性.笔者提出的算法与常用的尺度不变特征转换（Scale Invariant Feature Transform,SIFT)算法和尺度Harris算法在复现率上取得的结果如图2所示.

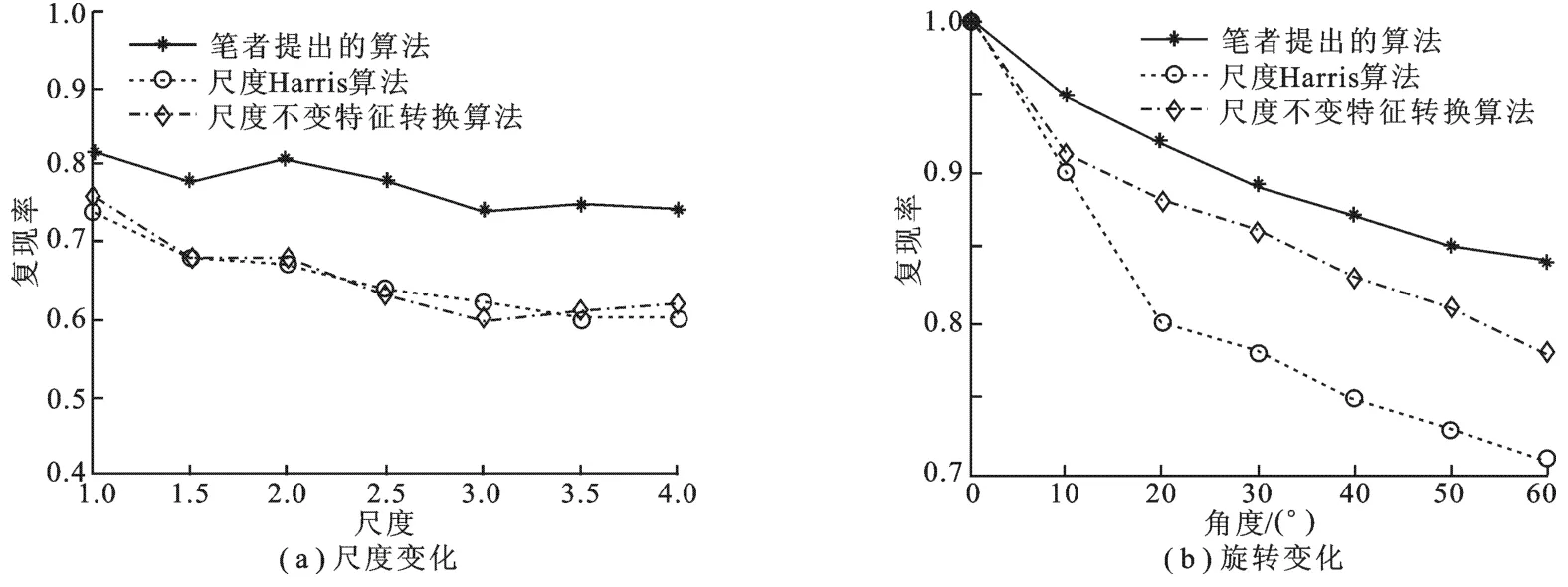
图2 尺度和旋转变化下的复现率

图2显示了在图像发生尺度和旋转变化时各种算法的复现率对比.笔者提出的算法在图像发生尺度变化和旋转变化的配准操作时,能够获得超过SIFT算法和尺度Harris算法的复现率.这是因为:笔者提出的算法中使用的特征点描述方法受图像信息的影响较小,序列描述子具有高度的尺度和旋转不变性,能够匹配更多的有效特征点对.较高的复现率表明,笔者提出的算法在图像特征点检测和匹配上是有效的和准确的.

3.2 对比结果

笔者使用图像处理中常用的检测图像和实际拍摄图像进行各种情况下的图像配准,验证笔者提出的算法的性能.检测图像如图3所示,图3（a)为测试图像“Boat”,图3（b)为3幅变换图像;图3（c)为测试图像“Bark”,图3（d)为3幅变换图像;图3（e)、（f)和（g)为3对实际拍摄的待配准图像.

为了进一步对笔者提出的算法进行检验,采用复现率、有效点对数量和运行时间对算法进行分析.实验的硬件环境为CPU 2.1 GHz,内存为2 GB,操作系统为Win7,程序开发平台为Matlab2012.笔者提出的算法与SIFT算法和尺度Harris算法在上述3个指标上的运行结果如图4所示.图4中横坐标1到9分别表示图3中的测试图像对,其中1到3为图3（a)与3幅变换图像的配准结果,4到6为图3（c)与3幅变换图像的配准结果,7到9为图3（e)、（f)和（g)的配准结果.

图3 检测图像

图4 算法性能对比

为了达到实验结果的公平性,对比的3种方法均使用高斯差分算子进行特征点检测.因此,每组检测图像在3种方法下的特征点数量和位置都是一致的,差别只在于特征点的描述方式和匹配算法.在多数情况下,笔者提出的算法能够在3种算法的对比中取得最优的复现率,最大的有效点对数量和最短的运行时间.

图3（a)～（b)中的检测图像包含了尺度和旋转变换,而且图像内容丰富,纹理复杂,该组图像中检测到的特征点数量最多,笔者提出的算法在运行时间上的优势非常明显.图3（e)的检测图像中包含了尺度变换和图像剪裁,该组图像中的特征点间的空间位置关系存在很大差异,笔者提出的算法在运算时间上变长是因为增加了算法的迭代次数.图3（f)的检测图像中存在大量相似的局部结构,这种情况是图像配准的难点,笔者提出的算法仍然保持了较高的复现率,因为文中定义的SDAO是一种结合了局部结构和全局信息的特征点描述方式.

笔者提出了一种基于特征点描述和匹配的图像配准算法.实验结果表明:与传统算法相比,笔者提出的算法具有较高的复现率和较短的运算时间,是一个准确、快速的图像配准算法.

[1]吴伟交,王敏,黄心汉,等.基于向量夹角的SIFT特征点匹配算法[J].模式识别与人工智能,2013,26(1):123-127. Wu Weijiao,Wang Min,Huang Xinhan,et al.SIFT Feature Matching Algorithm Based on Vector Angle[J].PatternRecognition and Artificial Intelligence,2013,26(1):123-127.

[2] 唐朝伟,肖健,邵艳清,等.一种改进的SIFT描述子及其性能分析[J].武汉大学学报:信息科学版,2012,37(1):11-16. Tang Chaowei,Xiao Jian,Shao Yanqing,et al.An Improved SIFT Descriptor and Its Performance Analysis[J]. Geomatics and Information Science of Wuhan University,2012,37(1):11-16.

[3]Zhang K,Li X,Zhang J.A Robust Point-matching Algorithm for Remote Sensing Image Registration[J].IEEE Geoscience and Remote Sensing Letters,2014,11(2):469-473.

[4]Wu Y,Ma W,Gong M,et al.A Novel Point-matching Algorithm Based on Fast Sample Consensus for Image Registration[J].IEEE Geoscience and Remote Sensing Letters,2014,1(99):1-5.

[5]Aguilar W,Frauel Y,Escolano F,et al.A Robust Graph Transformation Matching for Nonrigid Registration[J].Image and Vision Computing,2009,27(7):897-910.

[6]Liu Z,An J,Jing Y.A Simple And Robust Feature Point Matching Algorithm Based on Restricted Spatial Order Constraints for Aerial Image Registration[J].IEEE Transactions on Geoscience and Remote Sensing,2011,8(4):805-841.

[7]Wang J,Zhou Y,Bai X,et al.Shape Matching and Recognition Using Group-wised Points[J].Advances in Image and Video Technology,2012(7088):393-404.

[8]Gong M,Zhao S,Jiao L,et al.A Novel Coarse-to-fine Scheme for Automatic Image Registration Based on Sift and Mutual Information[J].IEEE Transactions on Geoscience and Remote Sensing,2014,52(7):4328-4338.

[9]Ojala T,Pietikainen M,Maenpaa T.Multiresolution Grayscale and Rotation Invariant Texture Classification with Local Binary Patterns[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(7):971-987.

[10]Heikkila M,Pietikainen M,Schmid C.Description of Interest Regions with Local Binary Patterns[J].Pattern Recognition,2009,42(3):425-436.

（编辑:郭 华)

Fast and precise image registration algorithm

JIN Feng1,2,FENG Dazheng2
(1.School of Computer Science and Technology,Xidian Univ.,Xi’an 710071,China; 2.National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China)

An image registration algorithm is proposed through the analysis of the objective function. There are two optimal solutions to the function:the biggest number of efficient point pairs and the image transformation matrix with the highest accuracy,which can be solved by two different point matching matrices.The algorithm gets the transformation matrix by the points described in the center symmetric local binary pattern(CS-LBP),and obtains the efficient points by the statistical deflection angle order (SDAO).The SDAO is a sample and accuracy descriptor that integrates the local structure and global information of images.By combining with the advantages of the two description methods,the algorithm achieves a high alignment accuracy and a small computational volume.

image registration;point matching;descriptor;center symmetric local binary pattern;spatial order property

TP391.4

A

1001-2400（2015)06-0088-06

10.3969/j.issn.1001-2400.2015.06.016

2014-06-20

时间:2015-03-13

国家自然科学基金资助项目（61271293)

靳 峰（1982-),男,西安电子科技大学博士研究生,E-mail:xdjinfeng@163.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20150313.1719.016.html