利用TMF和置信传播的无监督SAR图像分割

甘 露,吴 艳,王 凡

(西安电子科技大学电子工程学院,陕西西安 710071)

利用TMF和置信传播的无监督SAR图像分割

甘 露,吴 艳,王 凡

(西安电子科技大学电子工程学院,陕西西安 710071)

针对三重马尔可夫场模型传统统计推断方法无法兼顾分割精度和计算效率的问题,提出了一种高效的利用置信传播的三重马尔可夫场模型统计推断方法,并应用于无监督合成孔径雷达图像分割.该算法结合三重马尔可夫场模型和合成孔径雷达图像统计特性,将图像分割问题转化为三重马尔可夫场的最大后验边缘估计问题.针对三重马尔可夫场中的两个标记场,将置信传播算法推广到二元情形,通过消息传递的方式估计双标记场的联合后验边缘概率,并依据最大后验边缘准则同时实现两个标记场的估计.模拟图像和实测合成孔径雷达图像的仿真实验结果表明,该算法能有效抑制相干斑的影响,能以合理的计算代价获得精确的分割结果.

合成孔径雷达;图像分割;三重马尔可夫场;置信传播

合成孔径雷达（Synthetic Aperture Radar,SAR)系统因其全天时、全天候、高分辨、穿透性强等特点而广泛应用于军事和民用的各个领域.SAR图像分割作为SAR图像目标识别与解译技术的重要环节,一直是国内外学者研究的热点[1-3].然而,受相干成像机制的影响,SAR图像含有大量的相干斑噪声,使得SAR图像分割成为一个极具挑战性的难题.

在众多图像分割算法中,马尔可夫随机场（Markov Random Field,MRF)模型[4]因其能够充分考虑图像局部相关性,在处理简单图像的分割问题时取得了很好的结果,但在处理非平稳SAR图像时,则处理效果不理想.三重马尔可夫场（Triplet Markov Fields,TMF)[5]模型通过引入一个辅助场来描述图像的非平稳特性,在处理非平稳SAR图像分割问题时取得了令人满意的结果[6-8].然而,TMF模型的统计推断仍然是一个难题.现有算法通常采用最大后验边缘（Maximization of the Posterior Marginal,MPM)准则[9],利用Gibbs采样估计后验边缘概率.然而,由于Gibbs采样收敛缓慢,经过有限次的迭代其后验边缘概率的估计值可能远离真实值,使得算法无法兼顾分割精度和计算效率.

近年来随机场模型的统计推断方法受到了越来越多的关注,涌现出了许多新的高效方法,如图割[10]和置信传播[11-13].图割通过求解图的最小分割问题,实现了精确快速的最大后验（Maximum A Posteriori,MAP)推断;置信传播采用消息传递的方式来实现推断,在MRF的推断问题中表现出了优良的性能.更为重要的是,依据不同的消息更新准则,置信传播既可实现MAP推断（Max-Product算法[11]),又可实现MPM推断（Mum-Product算法[12-13]).而相关研究表明,MPM准则比MAP准则更适合于图像分割[9].因此,文中研究基于置信传播的MPM推断方法.

基于上述分析,关注MPM准则下TMF模型的高效统计推断,笔者提出了一种基于置信传播的TMF模型推断方法,并应用于无监督SAR图像分割.该方法结合了TMF模型对于非平稳SAR图像的精确建模能力和置信传播算法在统计推断中的高效性,针对TMF模型中的两个标记场,将标准置信传播算法推广到二元情形,定义双标记场条件下的消息更新准则和置信度计算公式,通过消息传递的方式来估计双标记场的联合后验边缘概率.基于该联合后验边缘概率,通过简单的计算就能够同时实现两个标记场的MPM估计.标记场的估计和参数的估计交替迭代进行,实现无监督的SAR图像分割.模拟图像和实测SAR图像的仿真实验表明,文中算法能有效抑制相干斑噪声的影响,以合理的计算代价获得精确的分割结果.

1 TMF模型分析

令S表示图像像素集,MRF模型包含两个定义在S上的随机场X=（Xs)s∈S和Y=（Ys)s∈S,其取值分别为Ω={ω1,…,ωk}和实数集R.统计分割的任务就是从可观测的Y=（Ys)s∈S中恢复出不可观测的X=（Xs)s∈S.当势能函数取决于基团的位置时,随机场（X,Y)在概率意义下是非平稳的.在TMF模型中,通过引入第3个随机场U=（Us)s∈S来描述p（x,y)的非平稳性.Us的不同取值可以描述（X,Y)的不同平稳态.不失一般性,假设待处理的非平稳图像具有两个不同的平稳态,即Us的取值Λ=（a,b).则马尔可夫场（X,U)的分布可通过如下能量函数定义[5]为

假设随机变量Y对（X,U)的条件分布满足p（y|x,u)=p（y|x),并且Y=（Ys)s∈S对于X=（Xs)s∈S条件独立,则T=（X,U,Y)的联合分布定义为[5]

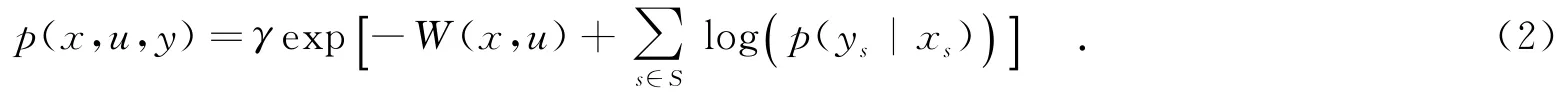
2 利用TMF和置信传播的无监督SAR图像分割

2.1 基于置信传播的TMF模型统计推断

统计分割框架通常通过最优化某种准则实现图像分割,如MAP准则或MPM准则.MPM准则的实质是,最小化错误分类像素个数的期望值,比MAP准则更适合于图像分割[9].在MPM准则下,分割就是对每个像素找一个最优的标记s,使得该标记的后验边缘概率最大,即

对于TMF模型,直接估计这一概率更为困难,因为标记场U也是不可观测的,同样需要估计.注意到（X,U)是一个MRF[6],这就为将两个标记场看作1个联合标记,直接估计联合后验边缘概率p（xs,us|y)提供了理论依据.基于p（xs,us|y),就可以通过简单的计算同时获得两个标记场的MPM估计.这样,MPM准则下的TMF统计推断问题,就转化为对于p（xs,us|y)的估计问题.Sum-Product置信传播[12-13]是解决这一类问题最有效的方法,该算法迭代地在图模型的节点之间传递局部消息,每一次迭代中消息得到更新,最终每个节点获得一个置信度,即为该节点的后验边缘概率.对于无环图模型,该算法可以获得精确的推断结果.而对于MRF这一类多环图,尽管该算法不能保证收敛,但在已知的大多数实验中都能够收敛到一个较好的近似解.因此,文中采用Sum-Product置信传播来解决TMF模型的MPM统计推断问题.

首先,式（2)中的TMF联合分布可因式化为

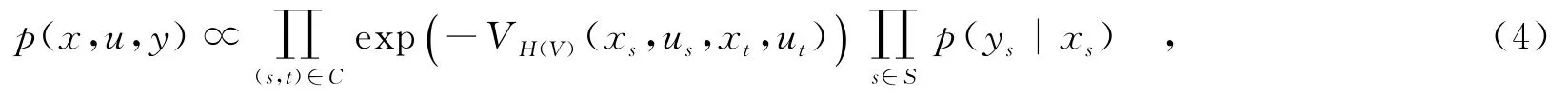
其中,VH和VV分别为水平和竖直基团的基团势函数,即

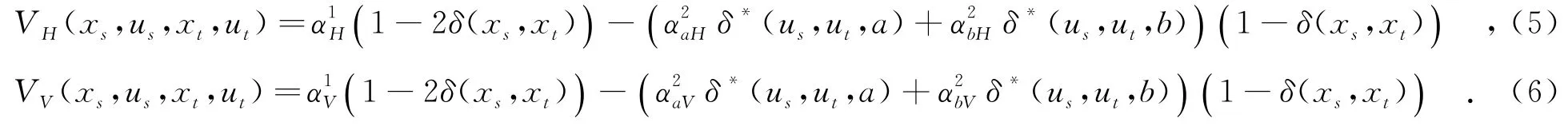
众所周知,Gamma分布可以很好地建模SAR数据,因此,采用如下似然分布:

其中,Γ（)为Gamma函数,L为等效视数,μi为标记xs=i的区域的均值.

式（4)给出的因式化TMF联合分布可以很方便地用图模型来表示,如图1所示.节点集V={vs},表示二元联合马尔可夫标记（X,U),Y={ys},为观测变量集合.置信传播算法通过迭代地在图模型节点之间传递局部消息来实现统计推断:每个标记节点接收其相邻标记节点传递来的消息,同时也向其相邻标记节点发送消息,而观测节点只向其对应的标记节点发送消息而不接收任何消息,如图1所示.令为第n次迭代中节点vt发送给其相邻节点vs的二元联合消息,b（xs,us)为节点vs的二元联合置信度.不同于标准置信传播算法,由于两个标记场的存在,对于TMF模型,每一个节点对应于1个联合标记对（xs,us),而每一个消息和置信度都是1个矩阵.在每次迭代中,消息更新依据Sum-Product准则,即

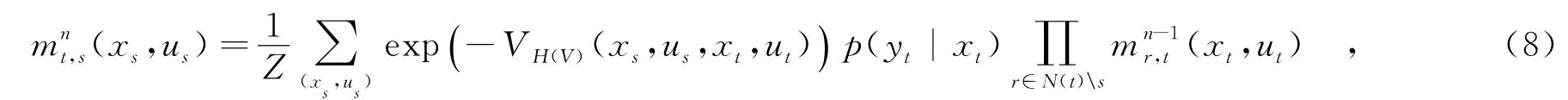
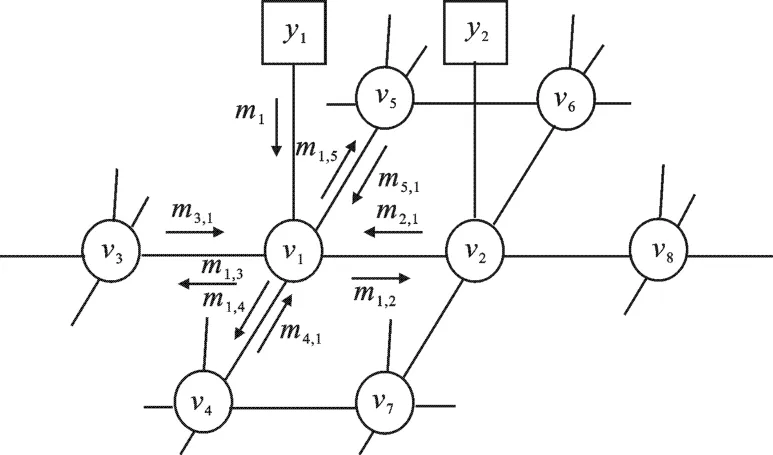
图1 TMF图模型及其局部消息传递示意图

其中,N（t)s表示除s外t的相邻节点集合,Z为归一化常数.

在N次迭代后,每个节点的二元联合置信度矩阵为该节点接收到的所有消息的乘积,即

该置信度矩阵即为联合后验边缘概率p（xs,us|y)的近似估计.基于该置信度矩阵,通过简单的求和计算即可获得该节点每个标记场的边缘后验概率,即

最终,依据MPM准则,可同时得到TMF模型中两个标记场的估计,即

2.2 无监督分割算法的实现过程

对于无监督分割,标记场x和u都是不可观测的,因此TMF先验模型参数θ和观测模型参数μ只能通过观测场y或标记场的中间估计结果来进行估计.这里采用迭代条件估计（Iterative Condition Estimation,ICE)[14]来估计模型参数.通过基于置信传播的TMF模型统计推断和基于ICE的参数估计迭代进行,实现无监督图像分割,算法具体实现过程如下:

步骤1 初始化标记场,x的初始化采用k均值聚类,u采用随机二值初始化.

步骤2 依据当前标记场,利用ICE算法估计参数值:

（1)依后验分布利用Gibbs采样获得m个样本;

（2)对每个样本利用最大似然方法估计μ,利用最小二乘法估计θ;

（3)对m个样本的参数估计值求期望.

步骤3 依据当前参数,利用置信传播算法实现TMF模型的MPM推断:

（1)初始化所有消息为1;

（2)利用Sum-Product置信传播算法依据式（8)和式（9)估计p（xs,us|y);

（3)基于p（xs,us|y)依据式（12)和式（13)估计x和u.

步骤4 判断是否收敛或达到最大迭代次数,否则,返回步骤2.

3 实验结果与分析

为验证文中算法的性能,分别对模拟图像和实测SAR图像进行了仿真实验.实验中选取两种算法与文中算法（记为TMF_BP)进行对比:文献[4]中基于MRF的分割算法（记为MRF)和文献[5]中基于TMF的分割算法（记为TMF).MRF和TMF算法中每个像素点执行30次Gibbs采样,而TMF_BP算法中置信传播算法的最大迭代次数同样设为30.

图2 模拟图像分割结果

3.1 模拟图像实验结果与分析

图2（a)为一幅受乘性相干斑噪声污染的非平稳模拟图像,大小为256×256,包含两类区域和两个平稳态,其真实分割结果和对应的U场划分如图2（b)和2（c)所示.3种算法的分割结果分别如图2（d)、图2（e)和图2（f)所示.MRF和TMF算法的分割结果对比验证了TMF模型的优越性.而文中TMF_BP算法的分割结果明显更为精确.为了定量地评价算法的性能,采用全局精度（Overall Accuracy,OA)作为评价指标. OA为正确分类像素占全部像素的百分比,高的OA值表示更好的分割性能.3种算法的OA值分别为87.63%、91.42%和96.87%.以上数据指标和分割结果验证了置信传播算法在TMF模型统计推断上的有效性.

图3 实测SAR图像分割结果

3.2 实测SAR图像实验结果与分析

选取5幅不同场景包含不同地物的实测SAR图像来验证文中算法对实测SAR数据的有效性.表1给出了实测SAR数据的先验信息.实测SAR图像分割结果如图3所示.从分割结果中可以看出,TMF算法的分割结果要优于MRF算法的,其误分割更少,分割区域更为平滑,并能有效保持细节信息,这充分体现了TMF模型对非平稳SAR图像建模的优势.TMF算法和TMF_BP算法的对比则说明了置信传播在统计推断中的优越性.由于Gibbs采样在有限次迭代后,边缘后验概率的估计值可能远离其真实值,因此容易陷入局部最小,使得TMF算法的分割结果没有很好地抑制相干斑噪声的影响,在平滑区域内部出现了较多的误分.相对于TMF算法,TMF_BP算法的分割结果更为平滑,区域一致性更好,表明置信传播算法获得了更为精确的边缘后验概率估计值.文中TMF_BP算法结合了TMF模型对于非平稳SAR图像的精确建模能力和置信传播在统计推断中的高效性,不仅能够有效抑制乘性斑点噪声的影响,获得更为平滑的分割结果,而且可同时使区域边界定位更为准确,有效保持原始图像信息.

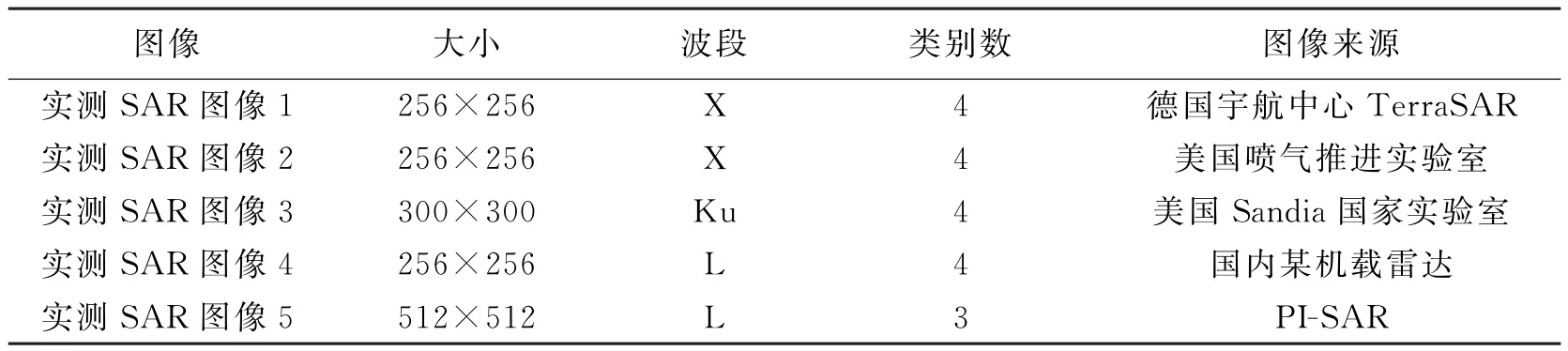
表1 实测SAR图像先验信息

为客观评价算法的性能,可选择两个SAR图像分割算法的客观评价指标[15],即比值图像的对数归一化似然比和方差描述了分割结果的区域同质性,其值越小,表明分割结果的区域一致性越好;描述了比值图像像素强度的起伏程度,其值越小,表明分割算法的性能越好.表2给出了3种算法分割结果的客观评价指标.从表2可以看出,TMF算法的总体指标要优于MRF算法的,验证了TMF模型的优越性.而文中TMF_BP算法的两项指标均要优于其他两种算法的,表明该算法能够有效抑制相干斑噪声的影响,获得更好的区域一致性.

表2 实测SAR图像分割性能客观评价指标

3.3 计算效率对比分析

从收敛速度和计算时间两方面比较TMF算法和TMF_BP算法的计算效率.图4给出了实测SAR图像1实验中Gibbs采样和置信传播的能量函数值收敛曲线.从图4可以看出,Gibbs采样收敛缓慢,而置信传播能够很快地收敛到一个更小的能量值,充分说明了置信传播算法的高效性.表3给出了所有实验中两个算法的计算时间对比.从表3可以看出,由于置信传播算法的高效性,使得TMF_BP算法的计算效率大大提高.

表3 两种算的法计算时间对比 s

4 结束语

笔者提出了一种利用TMF和置信传播的无监督SAR图像分割算法.该算法采用TMF模型,结合SAR图像的统计特性实现了更为精确的SAR图像建模.同时充分考虑到TMF模型中两个标记场的存在,利用Sum-Product置信传播算法实现高效的TMF模型统计推断,有效提高了基于TMF模型分割算法的分割精度和计算效率.模拟图像和实测SAR图像的仿真实验表明,相比于传统的基于MRF和TMF模型的SAR图像分割算法,文中算法能够以较小的代价获得更为精确的分割结果,取得了令人满意的结果.

图4 算法收敛曲线对比

[1]Shui P L,Zhang Z J.Fast SAR Image Segmentation via Merging Cost with Relative Common Boundary Length Penalty [J].IEEE Transactions on Geoscience and Remote Sensing,2014,52(10):6434-6448.

[2]Zhang H,Wu Q,Nguyen T,et al.Synthetic Aperture Radar Image Segmentation by Modified Student’s t-mixture Model[J].IEEE Geoscience and Remote Sensing Letters,2014,52(7):4391-4403.

[3]崔艳鹏,胡建伟,杨绍全,等.利用DT-Grow Cut的MSTAR SAR图像自动分割技术[J].西安电子科技大学学报,2011,38(3):150-154. Cui Yanpeng,Hu Jianwei,Yang Zhaoquan,et al.SAR Image Automatic Segmentation based on DT-GrowCut[J]. Journal of Xidian University,2011,38(3):150-154.

[4]Deng H,Clausi D.Unsupervised Segmentation of Synthetic Aperture Radar Sea Ice Imagery Using a Novel Markov Random Field Model[J].IEEE Transactions on Geoscience and Remote Sensing,2005,43(3):528-538.

[5]Benboudjema D,Pieczynski W.Unsupervised Statistical Segmentation of Nonstationary Images Using Triplet Markov Fields[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,39(8):1367-1378.

[6]Wang F,Wu Y,Zhang Q,et al.Unsupervised SAR Image Segmentation Using Higher Order Neighborhood-based Triplet Markov Fields Model[J].IEEE Transactions on Geoscience and Remote Sensing,2014,52(8):5193-5205.

[7]Lian X J,Wu Y,Zhao W,et al.Unsupervised SAR Image Segmentation based on Conditional Triplet Markov Fields [J].IEEE Geoscience and Remote Sensing Letters,2014,11(7):1185-1189.

[8]Zhang P,Li M,Wu Y,et al.Unsupervised SAR Image Segmentation Using a Hierarchical TMF Model[J].IEEE Geoscience and Remote Sensing Letters,2013,10(5):971-975.

[9]Corner M,Delp E.The EM/MPM Algorithm for Segmentation of Textured Images:Analysis and Further Experimental Results[J].IEEE Transactions on Image Processing,2000,9(10):1731-1744.

[10]Boykov Y,Veksler O,Zabih R.Fast Approximate Energy Minimization via Graph Cuts[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2001,23(11):1222-1239.

[11]Weiss Y,Freeman W.On the Optimality of Solutions of the Max-product Belief Propagation Algorithm in Arbitrary Graphs[J].IEEE Transactions on Information Theory,2001,47(2):723-735.

[12]Yedidia J,Freeman W,Weiss Y.Understanding Belief Propagation and Its Generalizations[C]//Proceedings of International Joint Conference on Artificial Intelligence.Seattle:Morgan Kaufmann,2001:239-269.

[13]Li J,Bioucas-Dias J,Plaza A.Spectral-Spatial Classification of Hyperspectral Data Using Loopy Belief Propagation and Active Learning[J].IEEE Transactions on Geoscience and Remote Sensing,2013,51(2):844-556.

[14]Salzenstein F,Pieczynski W.Parameter Estimation in Hidden Fuzzy Markov Random Fields and Image Segmentation [J].Graphical Models and Image Processing,1997,59(4):205-220.

[15]Caves R,Quegna S,White R.Quantitative Comparison of the Performance of SAR Segmentation Algorithms[J].IEEE Transactions on Image Processing,1998,7(11):1534-1546.

（编辑:齐淑娟)

Unsupervised SAR image segmentation using TMF and belief propagation

GAN Lu,WU Yan,WANG Fan
(School of Electronic Engineering,Xidian Univ.,Xi’an 710071,China)

To solve the problem that the traditional statistical inference approach for the triplet Markov fields(TMF)model cannot balance segmentation accuracy and computational efficiency,an efficient statistical inference approach for the TMF model using belief propagation is proposed,and then applied to unsupervised synthetic aperture radar(SAR)image segmentation.The algorithm combines the TMF model and the statistical property of the SAR image,and translates the segmentation problem into maximization of the posterior marginal(MPM)estimation.For the two label fields in TMF,the belief propagation algorithm is generalized to the bivariate case to estimate the joint posterior marginal probability of the two label fields through message passing.The two label fields can be simultaneously estimated according to the MPM criterion.Experiments on both simulated and real SAR images demonstrate that the proposed algorithm can efficiently suppress the influence of the speckle,and obtain accurate segmentation results with a reasonable computational cost.

synthetic aperture radar;image segmentation;triplet Markov fields;belief propagation

TN957.52

A

1001-2400（2015)06-0049-07

10.3969/j.issn.1001-2400.2015.06.009

2014-07-25

时间:2015-03-13

国家自然科学基金资助项目（61272281,61271297,61301284);高等学校博士点专项科研基金资助项目（20110203110001);中央高校基本科研业务费专项资金资助项目（WRYB142310,JDYB140507);陕西省自然科学基金资助项目（2015JM6288)

甘 露（1986-),男,西安电子科技大学博士研究生,E-mail:lgan@mail.xidian.edu.cn.

http://www.cnki.net/kcms/detail/61.1076.TN.20150313.1719.009.html