实值离散多窗Gabor变换窗函数求解快速算法

周高明,陶　亮,王华彬,李　锐

(安徽大学 计算智能与信号处理教育部重点实验室,安徽 合肥　230039)

实值离散多窗Gabor变换窗函数求解快速算法

周高明,陶亮*,王华彬,李锐

(安徽大学 计算智能与信号处理教育部重点实验室,安徽 合肥230039)

摘要:针对多窗实值离散Gabor变换(real-valued discrete Gabor transform，简称RDGT),综合窗簇与分析窗簇之间双正交性关系的窗函数计算复杂性高的问题,提出一种快速窗函数求解算法．该方法利用快速离散Hartley变换(discrete Hartley transform，简称DHT)及Hartley函数的正交性简化了窗函数的双正交条件关系式,从而降低窗函数计算复杂度．实验结果表明了该快速算法的高效性．

关键词:实值离散Gabor变换;多窗;快速算法

Gabor变换是有力的时频分析工具之一[1-5],Gabor变换的系数能够同时反映信号在时域与频域的局部化信息,这一特点使得Gabor变换在信号检测、图像压缩、图像识别等非平稳信号处理方面有广泛的应用[6-8]．传统复值离散Gabor变换(complex-valued discrete Gabor transform，简称CDGT)采用单个固定窗函数,具有固定的时频分辨率这一缺点．受窗函数时宽-带宽之间的制约关系,也即不确定性原理[9]限制,单窗CDGT时间分辨率和频率分辨率存在着矛盾关系,不可能同时最好．为改善单窗CDGT时频分辨率,文献[10-11]将传统单窗CDGT推广到多窗CDGT,但仅局限于框架理论,而且没有给出具体的快速算法,由框架理论求解多窗函数有局限性,相比之下,由双正交分析法求窗函数比框架理论方法简单、局限性小且易于给出快速算法[3]．另外,由于多窗CDGT比单窗CDGT的计算要复杂得多,研究快速多窗离散Gabor窗函数计算算法和快速多窗离散Gabor展开与变换算法,对Gabor变换的实时应用有重要意义．为此,Hu等[12]提出了基于高斯窗的多窗RDGT方法,这种方法由实数运算代替传统CDGT的复数运算,并且利用快速DHT(discrete Hartley transform)加快了运算速度,因而在求解满足双正交关系的对偶窗、变换系数以及信号重建等方面都比CDGT简单,易于硬件实现．作者在文献[12]的基础上推导出了一种多窗RDGT的窗函数的快速求解方法,这种方法利用Hartley函数的正交性可将原求解窗函数的双正交约束条件式简化,即将原非齐次方程组分解成若干独立的子方程组,然后分别求解各个降维后的子方程组,这样可以正确地求解分析窗并且节省了大量的计算时间．文中对比实验结果表明利用该方法求解窗函数具高效性．

1基于高斯窗的多窗RDGT

1.1单窗RDGT

设x={x(0),x(1),…,x(L-1)}是长度为L的有限长序列,将其以L为周期进行拓展,关于信号x的RDGT展开式和变换式分别定义为式(1)、(2)[4]

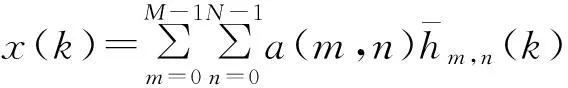
(1)

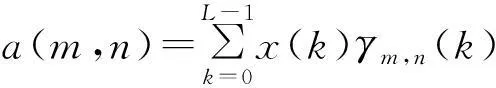
(2)

其中:分析窗函数h(x)和综合窗函数γ(x)也是以周期为L的进行拓展的有限长序列,如式(3)、(4)

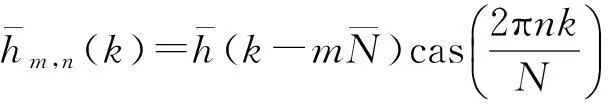
(3)

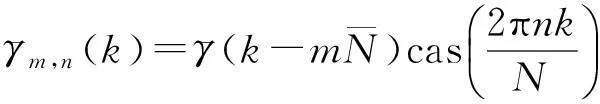
(4)

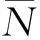
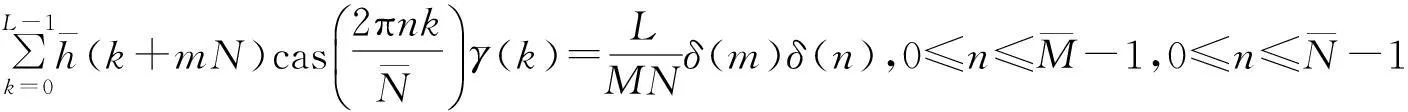
(5)

其中：δ(k)表示Kronecker delta．在给定综合窗的情况下,相关文献[2-3]论述了如何由双正交性关系式求解分析窗,这里不再赘述．

1.2多窗RDGT

设x(k)是离散时间周期为L的信号序列,关于x的多窗RDGT展开式和变换式定义如下[12]

(6)

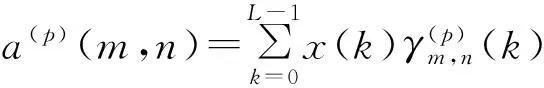
(7)

其中

(8)

(9)

h(p)(k)=α(-p/2)h(α(-p)k),α≥1，

(10)

cas(x)=sin(x)+cos(x)，

(11)

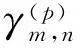
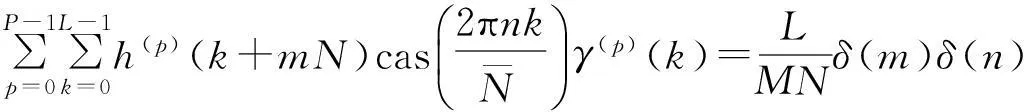
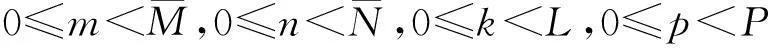
(12)

由式(12)可知,只要给出P个综合窗h(p)(k)即可求出对应的P个分析窗γ(p)(k),而且不难看出第p个分析窗γ(p)(k)不只是与第p个综合窗h(p)(k)有关,而是与全部P个综合窗h(p)(k)有关．式(12)矩阵形式可表示为

Hγ=v，

(13)

其中

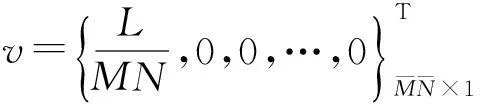
(14)

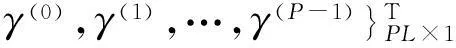
(15)

γ(p)={γ(p)(0),γ(p)(1)，…，γ(p)(L-1)}1×L，

(16)

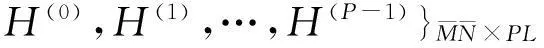
(17)

(18)

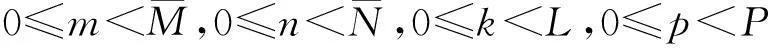
过抽样条件下(13)式中有多解,取其最小范数解,即

γ=HT(HHT)-1v.

(19)

2多窗RDGT窗函数的快速求解方法

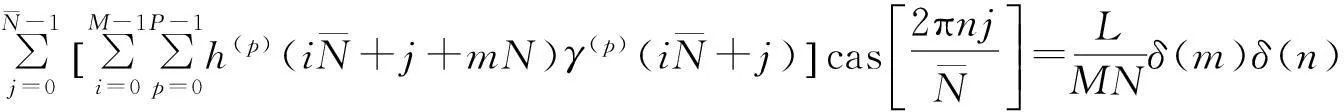
(20)

简写为

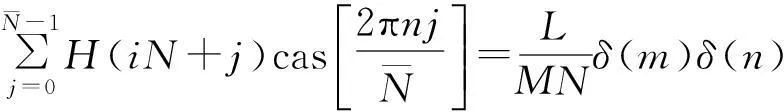
(21)

其中

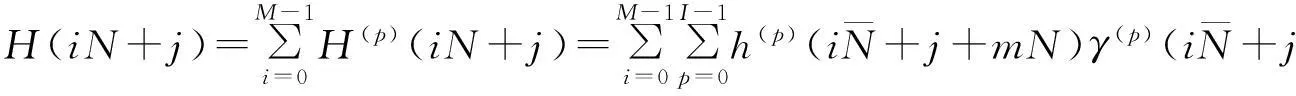
(22)

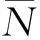
(23)

即

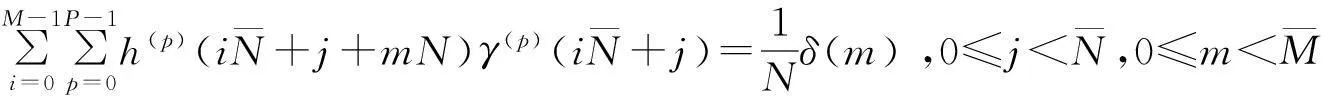
(24)

矩阵形式为

Hjγj=vj,

(25)

其中

(26)

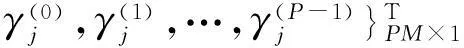
(27)

(28)

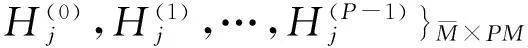
(29)

(30)

求解式(25),在过抽样条件下求其最小范数解是

(31)

3实验

实验使用编程工具是MATLAB R2013a、Windows 732位操作系统,系统内存4.00 GB．采用形式为式(32)所示.以长度为L=512点的离散高斯函数作为基本窗,如图1(a)所示.取综合窗的个数P=4,调制参数α=2,有

(32)

由公式(10)可求得子综合窗族h(p)(k),形如式(33),4个子窗的形状如图1(b)所示．

(33)

由快速算法求出的分析窗族和非快速算法求出的分析窗族分别如图1(c)～(f)所示.其中M=16,N=32,临界抽样,如图1c、1d所示;M=32,N=64,过抽样率为4,如图1(e)、1(f)所示．相同抽样条件下两种方法得到的差值如图1g、1h所示,差值控制在10-16～10-14数量级范围内,由此验证了论文提出的快速算法的正确性．

两种算法在不同抽样条件下的计算时间比较如表1所示,算法运行时间均是多次运行取平均值.由表1可以看出,在不同抽样条件下,采用论文快速算法求解分析窗所需要的计算时间比文献[12]的非快速算法明显减少,可以看出论文算法的高效性．两种算法在不同数量综合窗下的计算时间如表2所示,实验采取了过抽样条件(M=64,N=128), 算法运行时间均是多次运行取平均值.由表2可以看出,在不同数量的综合窗下,快速算法求解分析窗的时间均比非快速算法要少,这再次体现了论文算法的优越性．

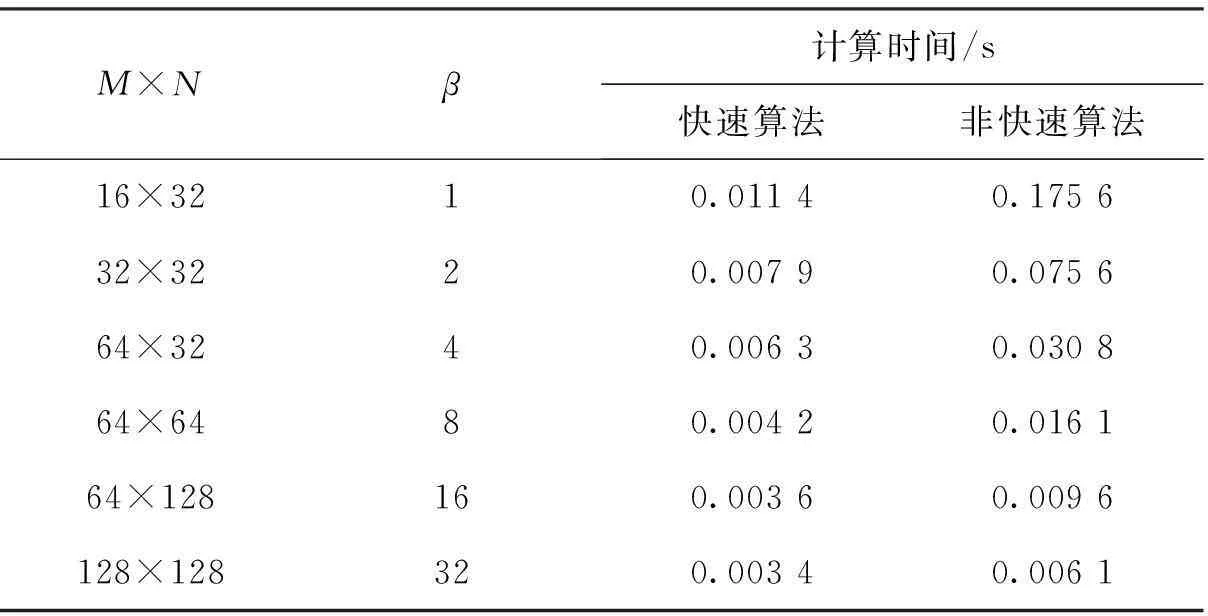
表1　两种算法在不同抽样点下的计算时间比较

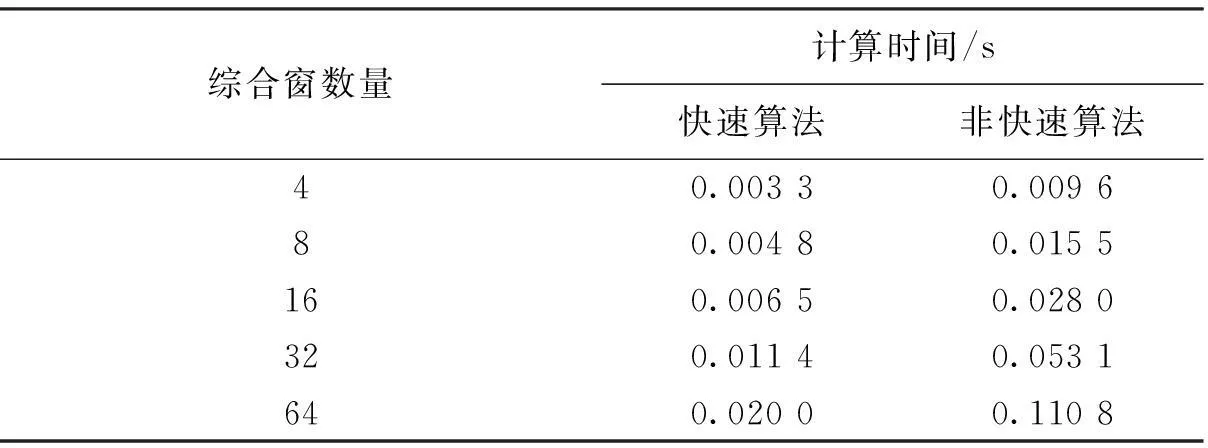
表2　两种算法在不同数量综合窗下的计算时间比较

4结束语

Gabor变换是广泛应用的时频分析方法之一,快速求解Gabor变换窗函数是Gabor变换算法首要解决的问题．论文首先回顾了基于高斯窗的单窗和多窗RDGT展开与变换理论,然后提出了一种采用双正交分析法计算M-RDGT窗函数的快速算法并给出了理论推导过程,最后通过实验验证了该方法的高效性．由于算法的本质是将大的线性方程组求解问题转化成多个彼此独立的小线性方程组的求解问题,再将各个独立的解综合得到分析窗的最终解的过程,由于多窗RDGT算法复杂性比单窗RDGT要高,考虑实时应用,可以将窗函数快速算法并行化实现加速变换,即将每个分解后的子方程组求解用一个并行通道去计算,下一步的工作可考虑采用并行处理方法进一步减少运算时间．

参考文献：

[1]Gabor D. Theory of communication: The analysis of information[J].J Inst Electr Eng, 1946,93(3):429-457.

[2]Wexler J, Raz S. Discrete Gabor expansions[J]. Signal Processing，1990, 21(3): 207-220.

[3]Qian S, Chen D. Discrete Gabor transform[J].IEEE Transactions on Signal Processing, 1993, 41(7): 2429-2438.

[4]Morris J M, Liu Y. Discrete Gabor expansion of discrete-time signals in l2(Z) via frame theory[J].IEEE Signal Processing Magazine, 1994, 40(2): 151-181.

[5]Daugman J G. Complete discrete 2-D Gabor transforms by neural networks for image analysis and compression[J]. Acoustics,Speech and Signal Processing, IEEE Transactions，1988, 36(7): 1169-1179.

[6]Lagae A, Lefebvre S, Dutre P. Improving Gabor noise[J]. IEEE Transactions on Visualization and Computer Graphics, 2011,17(8): 1096-1107.

[7]Cohen L. Time-frequency analysis[M].New Jersey:Prentice Hall,1995.

[8]Akan A, Chaparro L F.Multi-window Gabor expansion for evolutionary spectral analysis[J].Signal Processing, 1997,63(3):249-262.

[9]Zibulski M, Zeevi Y Y. Discrete multiwindow Gabor-type transforms[J].Signal Processing, IEEE Transactions on,1997, 45(6):1428-1442.

[10]Li S. Discrete multi-Gabor expansions[J].IEEE Transactions on Information Theory, 1999, 45(6):1954-1967.

[11]Balan R, Christensen J G, Krishtal I A, et al.Multi-window Gabor frames in amalgam spaces[J]. Mathematical Research Letters,2014,21(1):143-147.

[12]Hu X, Li R, Tao L. Multi-gabor expension and its fast algorithms based auxiliary biorthogonal function[J]. Journal of Computational Information Systems, 2013, 9(4): 1649-1657. multi-Gabor expansions[J].IEEE Transactions on Information Theory, 1999, 45(6):1954-1967.

[11]Balan R, Christensen J G, Krishtal I A, et al.Multi-window Gabor frames in amalgam spaces[J]. Mathematical Research Letters,2014,21(1):143-147.

[12]Hu X, Li R, Tao L. Multi-gabor expension and its fast algorithms based auxiliary biorthogonal function[J]. Journal of Computational Information Systems, 2013, 9(4): 1649-1657.

(责任编辑朱夜明)

Fast algorithm for window computation in multi-window

real-valued discrete Gabor transform

ZHOU Gao-ming, TAO Liang*, WANG Hua-bin, LI Rui

(Key Laboratory of Intelligence Computing and Signal Processing, Anhui University, Hefei 230039, China)

Abstract:To reduce the high complexity of the window computation using the biorthogonal relationship between the synthesis windows and the analysis windows in the multi-window real-valued discrete Gabor transform(M-RDGT), this paper presented a fast algorithm. It made the bi-orthogonal condition of computing basic window functions simpler by using fast discrete Hartley transform (DHT)and the orthogonality of the Hartley functions so that the computational complexity could be reduced. The experimental results of the algorithm also indicated that the proposed fast algorithm was more effective.

Key words:real-valued discrete Gabor transform; multi-window; fast algorithm

中图分类号：TP391

文献标志码:A

文章编号:1000-2162(2015)05-0031-06

作者简介：周高明(1990-),男,安徽安庆人，安徽大学硕士研究生;*陶亮(通信作者)，安徽大学教授,博士生导师,博士,E-mail:taoliang@ahu.edu.cn.

基金项目:国家自然科学基金资助项目(61372137);安徽大学信息保障技术研究中心课题 (ADXXBZ2014-11)

收稿日期：2015-02-10

doi:10.3969/j.issn.1000-2162.2015.05.006