砂土中埋设管线竖向抗拔特性研究

张 辉，于 龙，王 博，纪梦瑶，李 冰

(大连理工大学 建设工程学部，辽宁 大连116024)

海洋埋设管线屈曲破坏已成为危及管线运行和稳定性的重要课题[1]。为了降低运输的难度和避免石蜡分馏引起的固化，原油必须在高温高压下运输。正常工作条件下，管线内的温度一般会高于管线周围的环境温度。油气输运和暂停导致管线温度变化，此时在温度应力作用下会产生与管线铺设方向垂直的附加应力，一旦作用在管线上的上覆土压力小于此附加应力，管线就会发生运动。对于全埋式管线来说_，竖直方向土抗力要远远小于水平向土体抗力，而管线更倾向于向约束力较小的方向发生变形，所以本文只考虑管线的竖向屈曲情况。

目前对管线抗拔力主要采用数值分析和模型试验的方法进行研究。1986年 Boer等[2]研究了高温输油条件下埋设在砂砾石中管线的屈服破坏现象，将试验模型简化为平面应变问题，通过试验得到了管线在埋深为0.8 m时的位移和力的关系曲线。1990年，Schaminée等[3]进行了竖向运动时管线与土相互作用的模型试验研究。结果表明，最初开始上拔时土体的抗拔力急剧增加，然后在很短的时间内达到峰值，随后抗拔力趋于稳定。1997年 Croll等[4]研究了海底管线热屈曲的简化模型。此后，刘润[1]、Dickin[5]、Schupp[6]、Taylor[7]、Bransby 等[8]、Pedersen等[9]进行了管线上拔模型试验或者数值模拟试验，在此基础上得到管线的抗拔力。然而，以往的研究中给出的理论推导以及试验数据大都不尽相同，有的甚至有很大的差异，究其原因，主要在于研究者对砂土与管线的相互作用机理认识不同。

本文采用离散元分析和物理模型试验相结合的方法，分析砂土中埋置管线竖向拔出过程中土体抗力的变化特性以及砂土的流动机制，以期深入理解管线在砂土中的最大竖向抗拔力计算公式，并揭示管线与砂土的相互作用机理。

1 分析方法和过程

1.1 数值模拟

PFC2D程序采用细观力学参数表征砂土颗粒的力学性质。在PFC2D中，相对于圆形颗粒，簇颗粒由于形状的不规则，从而使颗粒间的咬合力有很大提高，进而更好地体现颗粒材料的应变软化现象。因此，本文利用 PFC二次开发的两种簇单元模拟砂土，如图1所示。此簇颗粒利用等面积法生成，即簇颗粒外轮廓线所围成的面积和原颗粒的面积相同。图中r0为原颗粒的半径，第一种簇颗粒由两个相同的圆颗粒组成，半径r1=0.84r0，圆心到原颗粒圆心的距离0.72r0;第二种簇颗粒由三个相同的圆颗粒组成，半径 r1=0.59r0。

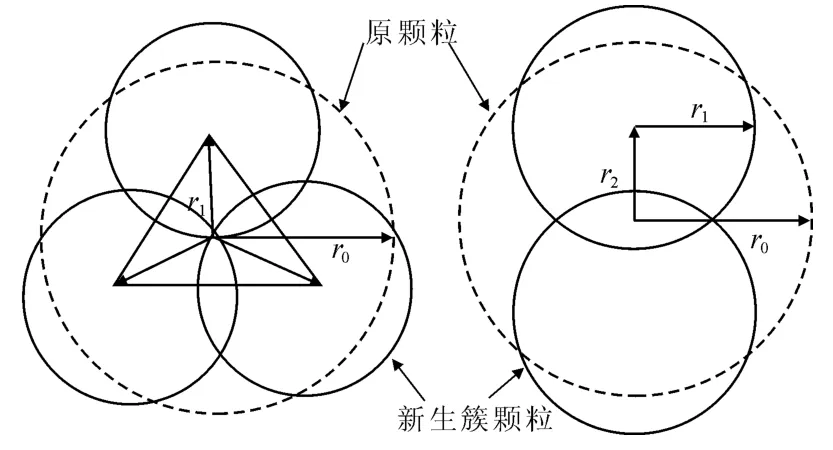
图1 砂土颗粒数值模拟(簇颗粒)

砂土数值模型采用落雨法[10]生成，首先在尺寸为2 m×0.72 m的空间内，高度为0.8 m的位置以每隔10 mm间距随机生成圆形颗粒，并在圆形颗粒的位置生成簇颗粒，再删除原颗粒，施加重力使簇颗粒自由落体，每隔8 000步生成一次簇颗粒，直至堆积到所要试样高度，最后进行平衡迭代直至颗粒最大速度小于1×10－4m/s。此时认为砂土数值模型已经生成。然后在管线埋置位置删除土颗粒，生成圆形墙体模拟管线，再次进行平衡迭代至颗粒最大速度小于1×10－4m/s，此时认为整个数值模型已完全建立，如图2所示。最终生成砂土的级配曲线如图3所示。

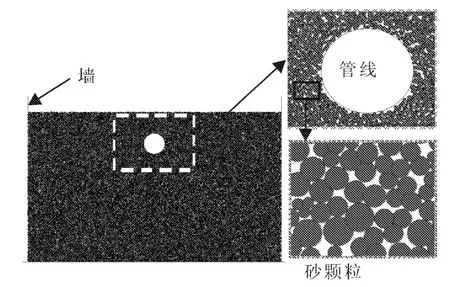
图2 埋设管线数值模型

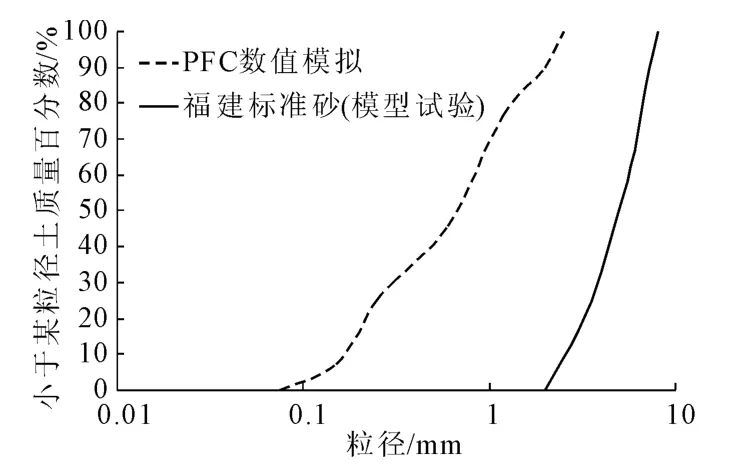
图3 数值模拟和模型试验级配曲线对比

在PFC2D中，颗粒之间的接触参数主要有颗粒刚度(其中包括法向刚度Kn和切向刚度Ks)、颗粒密度、颗粒阻尼系数和摩擦系数。本文以福建标准砂堆出的相对密度为Dr=55%的中密砂试样的物理参数[11－13]为基础(见表1和表2)，通过调整颗粒间参数并进行双轴压缩计算的方法，使砂土数值模型与物理模型具有一致的力学参数。

从表2中数据可以看出，离散元数值模型土样摩擦角与实际中密标准砂十分接近。

表1 PFC2D砂土颗粒微观参数

表2 数值砂土模型和实际堆积模型物理参数对比

由于离散元模型中颗粒粒径比实际大一个数量级且形状不可能完全一致，剪胀角同实际标准砂相比有明显差异。

本文数值分析主要模拟管线在不同埋深(H/D=1，2，3，4)情况下，竖向运动时受到砂土抗力的情况，其中，管线模型直径为D=100 mm，埋深H为管线中心位置到砂土表面的距离。用PFC软件中FISH语言编写程序，使管线以0.003 m/s的速度往上竖直运动，同时监测管线所受土压力。

1.2 模型实验

本文模型实验采用大连理工大学三轴实验室液压伺服加载系统，通过作动器控制管线的运动。

综上所述,利用0.25 mg/mL的NaCl溶液处理萝卜种子,能够提高萝卜芽苗菜的鲜质量和异硫氰酸盐的含量,同时对种子发芽和种子活力不会产生不良影响。因此我们建议在萝卜芽苗菜培养过程中添加0.25 mg/mL的NaCl,在保证产量的前提下将获得更具保健功能的萝卜芽苗菜。

模型管线直径为100 mm，长度为367 mm，放置在宽度370 mm、长2 000 mm、高800 mm的土槽中，模拟平面应变条件下管线上拔。埋深率为H/D=1、2、3和4.2，土样选用福建标准砂，采用落雨法分层堆置，每堆10 cm砂测量一次重度，控制整个试样重度为17 400 N/m3(也即相对密度为55%，中密砂)，最终堆积土样状态如图4所示。这样堆积出的砂土试样其力学特性如表2所示。

图4 液压伺服加载系统和实验设备

利用液压伺服加载系统的位移控制，通过作动器以及连接杆使模型管线以0.0125 mm/s的速度竖直向上运动，同时，用相机拍摄管线和周围土体运动状态(5 s拍摄一次)，用于进行PIV分析。

2 结果与分析

2.1 不同埋深所受土体抗拔力

图5给出了数值模拟和模型试验中不同埋深率下管线抗拔力－位移曲线，从图5中可以看出，无论是数值模拟还是模型试验，管线抗拔力随着埋深率(H/D)的增加而增大，同时达到峰值时上拔的位移随之增大，但最终不会超过 10 mm，也即为小于0.1D，这点和刘润[14]结果相同。另外，埋深率越大，砂土的应力软化现象也越明显，在模型试验结果中尤为明显。

图5 不同埋深率抗拔力－位移曲线

将数值模拟和模型试验结果中管线的极限抗拔力用HDLγ进行无量纲化处理，其中L为管线长度，γ为土的重度，并与文献[15－17]中的理论公式以及试验结果作了比较，比较结果如图6所示。可以看出，本文数值模拟和模型试验吻合较好，两者的结果都在已有文献结果上下限范围内。

从图5中抗拔力曲线的整体发展趋势来看，数值模拟和模型试验峰值后的软化特性并不一致。模型实验中，抗拔力从峰值处到稳定阶段所需的上拔位移比数值模拟要少的多。这是因为，PFC数值分析中的土体颗粒大小和形状不能同实际砂土完全一致。受计算效率的限制，本文PFC计算中粒径级配比模型实验实际砂土大一个数量级;另外，数值粒径尽管采用了两种不同的簇，同实际砂土颗粒相比仍光滑得多。这两个原因导致了在峰值抗拔力之后数值模拟和模型试验砂土的软化特性有所区别。

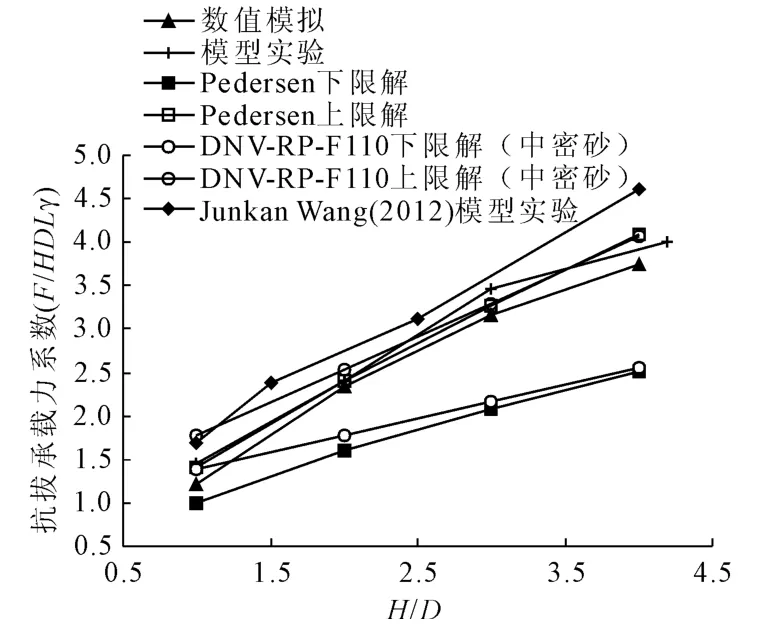
图6 峰值承载力系数－埋设率关系

2.2 砂土流动机制分析

无论是数值模拟还是模型试验，本文都是在浅埋条件下模拟管线的上拔行为。下面以埋深率H/D=2为例，对上拔过程中砂土的流动机制进行分析。

图7 不同颗粒级配的抗拔力系数与位移曲线关系

图8 模型试验PIV分析结果

(1)抗拔力发展阶段。最开始上拔时，砂土破坏面由管线顶部向土体表面迅速发展，由最开始的近似椭圆形发展到贯穿至土体表面，这一过程中抗拔力迅速提高。在抗拔力达到峰值时，砂土流动机制如图8(b)所示，管线上部土体形成一个倒楔形破坏带，值得注意的是，以往的理论推导对埋深H起始位置的定义，要么是从管线中心位置开始，要么是从管线顶端开始，而图8中该破坏带由管线“肩部”(即在管线中心位置距管线顶端的某一位置处)向上发展，破坏面与竖直方向的夹角约为18.25°，破坏带底部距管线中心位置的竖向距离约为0.4D。另外，在管线的两侧也有部分砂土颗粒明显回流。

(2)抗拔力软化阶段。导致抗拔力软化的原因有两方面:其一，随着剪应变的增加，砂土的内摩擦角由直剪试验测得的峰值38°软化至临界值30°;其二，随着继续上拔，管线上方土体整体向上移动，同时左右两条剪切破坏带之间的夹角逐渐减小，如图8(b)和图8(c)所示，管线上部土体的整体变形范围不断缩小。砂土强度的应变软化和剪切带的收窄，共同导致了砂土承载力的明显软化。本文测得的曲边梯形破坏面，其形状同 Byrne等[18]结果类似。

(3)抗拔力软化后稳定阶段。随着管线继续上拔，砂土达到临界状态后，其内摩擦角保持稳定;剪切带收窄至竖直向上的两条直线，如图8(d)所示，呈直面破坏模式，也达到了稳定状态。因此，在阶段Ⅲ，若忽略一些工况承载力的震荡，管线抗拔力总体呈稳定降低的趋势。抗拔力降低的原因是由于管线的埋深随着上拔而稳定地减小。

PFC数值计算所得土体流动机制如图9所示。比较图9(b)和图8(b)可以看出峰值承载力时数值计算同模型试验所得土体流动机制接近，这说明数值计算峰值抗拔力同模型试验是相吻合的。而数值计算抗拔力软化后稳定阶段，左右两条剪切带仍保留一定夹角，这就是数值计算残余抗拔力比模型试验高的原因。导致这一现象的原因，可能是数值计算粒径比模型试验粒径大所造成的。

2.3 粒径颗粒影响数值模拟与模型试验结果的验证

为了验证数值计算粒径对上述原因的影响，本文又做了有关砂砾石(颗粒粒径2 mm～5 mm，重度γ=15 049 N/m3)的模型实验，以工况 H/D=2，D=100 mm为例，为了去除试样重度、相对密度、模型管尺寸对结果的影响，将抗拔力进行归一化处理，对比如图7。

从图7可以看出，数值模拟和砂砾石模型试验的抗拔力系数和位移关系曲线吻合度很高，同时，数值模拟中所模拟的砂土粒径(2 mm～8 mm)与砂砾石模型试验粒径(2 mm～5 mm)也比较接近，这就直接证明了上述的猜想，的确是颗粒粒径大小影响了峰值后抗拔力软化的速度以及残余抗拔力的大小。

图9 数值模拟砂土颗粒增量位移场

3 结论

本文用数值模拟和模型实验的方法研究了砂土中埋设管线抗拔承载力以及上拔过程中砂土的流动机制。对比数值模拟和模型试验结果可知:

(1)用离散元程序PFC2D能够较好地模拟管线的竖直上拔过程。通过设置相关参数，能够得到相似的内摩擦角。但土样的剪胀特性同粒径尺寸和形状有关，受计算量的限制，目前用PFC2D模拟真实粒径尚有困难;

(2)砂土上拔过程中抗拔力变化分为三个阶段，即抗拔力发展阶段、软化阶段和残余稳定阶段。峰值抗拔力是砂土剪切带呈上宽下窄的梯形，抗拔力软化阶段剪切带逐渐收窄，最后抗拔力残余稳定阶段剪切带竖直向上;

(3)通过对砾石中管线抗拔力的研究发现，数值分析和砾石模型试验吻合较好，这也证明了颗粒粒径对管线抗拔力软化阶段影响很大，其直接影响残余抗拔力的大小和到达稳定阶段时管线的上拔位移。

[1]刘 润，闫澍旺，王洪播，等.砂土对埋设管线约束作用的模型试验研究[J].岩土工程学报，2011，33(4):559-565.

[2]Boer S，Hulsbergen C H，Richards D M，et al. Buckling considerations in the design of the gravel cover for ahigh temperature oil line[C]//Proc.18thOTC， Houston，1986.

[3]Schaminée P，Zorn N，Schotman G. Soil response for pipelineupheaval buckling analyses:full-scale laboratory tests andmodelling[C]//Offshore Technology Conference. Houston，Texas:OTC，1990.

[4]CrollJames. A simplified model of upheaval thermal buckling of subsea pipelines[J]. Thin-Walled Structures，1997:29:59-78.

[5]Dickin E A. Uplift resistance of buried pipelines in sand[J]. Soils and Foundations，1994，34(2):41-48.

[6]Schupp J，Byrne B W，et al.Pipeline unburial behaviour in loose sand[C]//Proc. 25thInternational Conference onOffshore Mechanics and Arctic Engineering. Hamburg，Germany，2006.

[7]Taylor N，Tran V C，Richardson D.Interface modelling for upheaval subsea pipeline buckling[C]//Prop. 21thOTC. Italy:Springer-Verlag，1989.

[8]Bransby M F，Newson T A，Brunning P，et al. Numerical and centrifuge modelling of the upheaval resistance of buried pipelines[C]//Proc. OMAE Pipeline Symposium.Rio de Janeiro，2001.

[9]Pedersen P T，Jensen J J. Upheaval creep of buried heated pipelines with initial imperfections[J]. Marine Structures，1988，1:11-22.

[10]刘 君，胡 宏.砂土地基中条形锚板抗拔模型试验的颗粒流数值模拟[C]//2012颗粒材料计算力学会议论文集.湖南，2012.

[11]Liu J，Hu H，Yu L. Experimental study on the pull-out performance of strip plate anchors in sand[C]//23rd International Offshore and Polar Engineering Conference，ISOPE，2013.

[12]刘 君，胡 宏.砂土地基锚板基础抗拔承载力PFC数值分析[J].计算力学学报，2013，30(5):678-682.

[13]Long Yu，Hui Zhang，Jun Liu. A discrete element study on upheaval ratcheting behavior of pipelines buried in sand[C]//ISFOG，2015.

[14]刘 润，李 彪，王洪播，等.砂土中埋设管线竖直向上运动时土抗力研究[J].岩土力学，2011，32(S1):28-32.

[15]Wang J. Monotonic and cyclic uplift resistance of buried pipelines in cohesionless soils[D]. London:University of Cambridge，2012.

[16]Det Norske Veritas，DNV －RP －F110(2007). Global buckling of submarine pipelines—structural design due to high temperature/high pressure[S]. Norway，2007.

[17]Nielsen N R，Lyngberg B. ＆ PedersenPT. Upheaval buckling failures of insulated buried pipelines:a case story[C]//Offshore Technology Conference. Houston，Texas，U.S.A. 1990.

[18]Byrne B W，et al.Experimental modeling of the unburial behavior of pipeline[C]//Offshore Technology Conference. Texas，USA，2008.