长春地铁暗挖隧道围岩参数智能位移反分析

王志斌，麻凤海，张碧雪

(大连大学 建筑工程学院，辽宁 大连116622)

城市地铁车站、区间的施工大多采用在地下岩土体内进行的暗挖施工，洞室开挖会破坏岩土体原有的天然平衡状态，引起地铁周围岩土体的应力重分布和地下水的重分布，极易导致岩土体失稳。岩土体参数的准确获得对于地表变形量的计算和围岩稳定性评价都具有重要的影响。在实际工程中，岩土体参数的获得往往依赖于室内试验和工程经验，存在“尺寸效应”及随机性大等诸多不足，且不能反映工程区域内岩土体的整体特性。运用智能位移反分析的方法通过现场位移监测值确定岩土体的重要参数，能够很好的解决这一问题[1]。

岩土工程中，所谓智能位移反分析[2]，是通过现场监测得到的能够反映岩土体力学行为的位移值，运用BP神经网络、遗传算法、蚁群算法等智能技术建立反分析模型[3]，反演计算得到岩土体的一个或多个初始参数。通过位移反分析得到的岩土体力学参数是一种综合考虑了岩土体特征、构造、施工中的各种未知因素的“综合参数”(亦称等效参数、灰参数)。运用这种“综合参数”通过数值分析求得的隧道围岩的位移值更加符合工程实际[4]，对于地铁隧道围岩稳定性的分析及变形预测有重要的指导意义。

1 工程概况

本文选取长春地铁解放大路站～自由大路站区间为研究对象，进行岩体参数的位移分析。区间左线范围为:K19+472.234—K19+772.234，长度300 m。区间隧道埋深约21 m，采用台阶法施工，断面为标准断面，宽6.2 m，高6.5 m。区间范围内涉及的地层自上而下主要有杂填土、粉质黏土、砾砂、全风化泥岩、强风化泥岩及中风化泥岩。区间隧道开挖区域地层主要为强风化泥岩。隧道平面及监测断面ZDB570位置见图1。选取典型断面ZDB570处的拱顶下沉和净空收敛位移值用于智能位移反分析，通过对该断面拱顶下沉和净空收敛监测数据的整理分析得到拱顶下沉最终值为17.02 mm，净空收敛最终值为6.16 mm。两项位移值都在施工安全控制值以内。

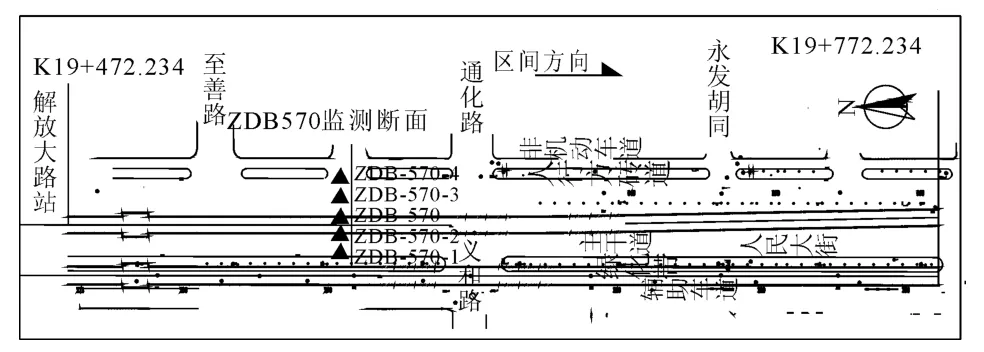
图1 隧道平面布置图

2 三维正算模型的建立

2.1 模型尺寸和边界的确定

采用Midas GTS NX有限元软件[5]进行隧道开挖施工模拟。取典型断面ZDB570附近暗挖段为模拟对象。模型选用莫尔 －库伦本构模型[6]，并简化为各向同性体进行分析。区间为标准断面，洞径6.2 m，洞高6.5 m。隧道埋深大约为21 m，建模时，以标准断面边缘为基准，左右各取21.9 m，向上取至地表为21 m，向下取23.5 m，保证了开挖面上下左右范围都在3倍洞径以外。隧道长度方向取30 m，满足研究的需要，又便于计算。模型中以隧道开挖的方向为Y轴，水平面内以隧道轴线垂直方向为X轴，铅直向上方向为Z轴，则整个数值计算区域范围:XYZ=50 m×30 m×50 m，计算模型见图2。

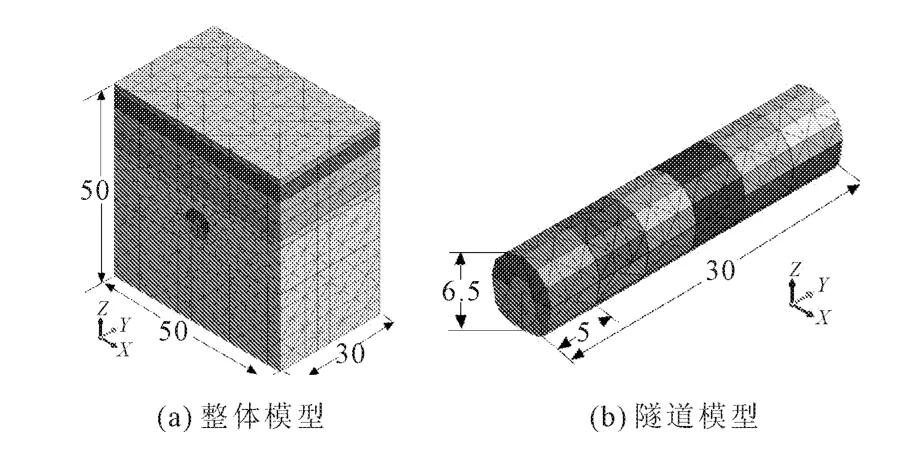
图2 数值计算模型(单位:m)

选用四面体单元进行有限元网格划分，共生成28325个单元和7602个节点。经多方面综合考虑，四周采用滑动约束，底部采用固定约束。

2.2 模型材料参数的确定

模型材料参数见表1，本文所做的工作为围岩参数的反分析，因此，该表中的岩土力学参数只是建模时的参考输入值，用于模型试算。所用参数是通过敏感性分析方法确定，并运用神经网络对参数进行反分析得到的。

在数值模拟中，对于超前小导管注浆加固的模拟，采用等效加固区的方法进行。根据小导管的尺寸、布设范围及注浆情况等综合因素确定加固区参数;初支用面板单元来模拟，软喷厚度根据初次支护喷混厚度确定为250 mm，一个进尺内的初支结构如图3。

表1 模型材料参数表

图3 软喷支护断面图模型

2.3 施工阶段模拟

区间采用上下台阶法施工，见图4，开挖进尺为5 m，隧道总长30 m，经过6次推进，隧道开挖结束。在数值模拟中将施工过程分为以下步骤进行:(1)初始地应力状态;(2)开挖上台阶土体①;(3)进行拱顶软喷支护;(4)开挖下台阶②、③部分土体;(5)进行②、③部分两侧的软喷支护;(6)开挖核心土④;(7)进行拱底软喷支护;(8)重复(2)～(7)步骤5次至30 m长隧道开挖完毕。

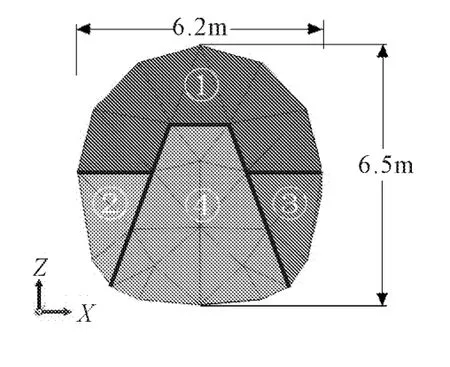
图4 隧道模型断面图

3 反分析参数的确定

目前，已知的监测数据有暗挖区间隧道拱顶下沉和净空收敛两个参数，即能辨识的参数个数为2。从数学理论上分析，为了保证反分析结果解的唯一性和避免出现解的不适应性，在输入的已知变量为2的情况下，能够进行反分析的未知变量的个数为1或2。对地表沉降和围岩变形有影响的岩体力学参数有很多，各个参数对围岩变形的影响因素有大有小，若对各个参数都进行反分析，不仅计算量巨大，而且结果的应用性也不强。因此，需要对各个参数做敏感性分析，找出主要的影响因素[7]，从而确定对围岩变形起主要影响作用的力学参数，对相关参数的敏感性程度进行评价，从而保证反分析的合理性和有效性以及数值模拟结果的可靠性[8]。

[9]中对敏感度的定义为:

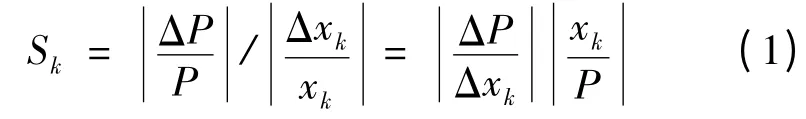
式中:Sk为因素xk的敏感度，k=1，2，3，…n，|ΔP/P|为系统特征的相对变化率;|Δxk/xk|为某一因素的相对变化率。每次只变动其中一个因素，其他因素不做变动。根据地质勘察报告及相关规范确定每个因素选取的基准值及变化范围，分别对弹性模量E、泊松比μ、黏聚力c以及内摩擦角φ对地层变形的影响进行分析，得到每一组参数影响下的地表变形相对值，按照式(1)定义的敏感度进行计算，结果见表2。

表2 各参数对地表变形的敏感度

由表2可知，敏感性最强的两个岩体参数为弹性模量E和内摩擦角φ。所以，本文中将选取这两个参数进行智能位移反分析。

4 建立神经网络模型

4.1 获得训练样本

基于BP神经网络智能反分析的实现，需要充足数量的样本对神经网络进行训练[10]。为保证样本的均衡性、全面性，同时减少试验的次数，本文采用正交设计[11]的方法进行训练样本的构造，对反分析参数进行5水平划分，见表3。

表3 反演参数的划分水平

运用正交表L25(56)划分出待反演参数的25组组合[12]，将其分别代入已建立的三维正算模型中，求得对应的净空收敛和拱顶下沉的位移值。得到BP神经网络的训练样本，见表4。

4.2 确定神经网络结构

神经网络模型的建立是通过MATLAB神经网络工具箱实现的[13]。选用经典的三层神经网络结构。研究发现隐含层数为1的三层BP网络能够完成任意n维到m维的映射，闭区间的任何一个连续函数都能够用单隐层的BP神经网络逼近。因此，本文采用含有一个隐层的BP网络模型[14]。现场监控量测所得的数据有周边收敛和拱顶沉降两个已知位移，故BP神经网络的输入层节点数为2。本文所要反演的目标有内摩擦角φ和弹性模量E两个参数，故输出层节点数也为2。网络隐层节点数为10。

神经网络模型训练函数的选取:隐含层中输出函数选择S型的对数函数 Logsig，传递函数选择 S型正切函数 Tansig，训练函数选用 Trainlm，这种函数以梯度下降法学习，学习速率也是自适应的[10]。神经网络模型结构图见图5。

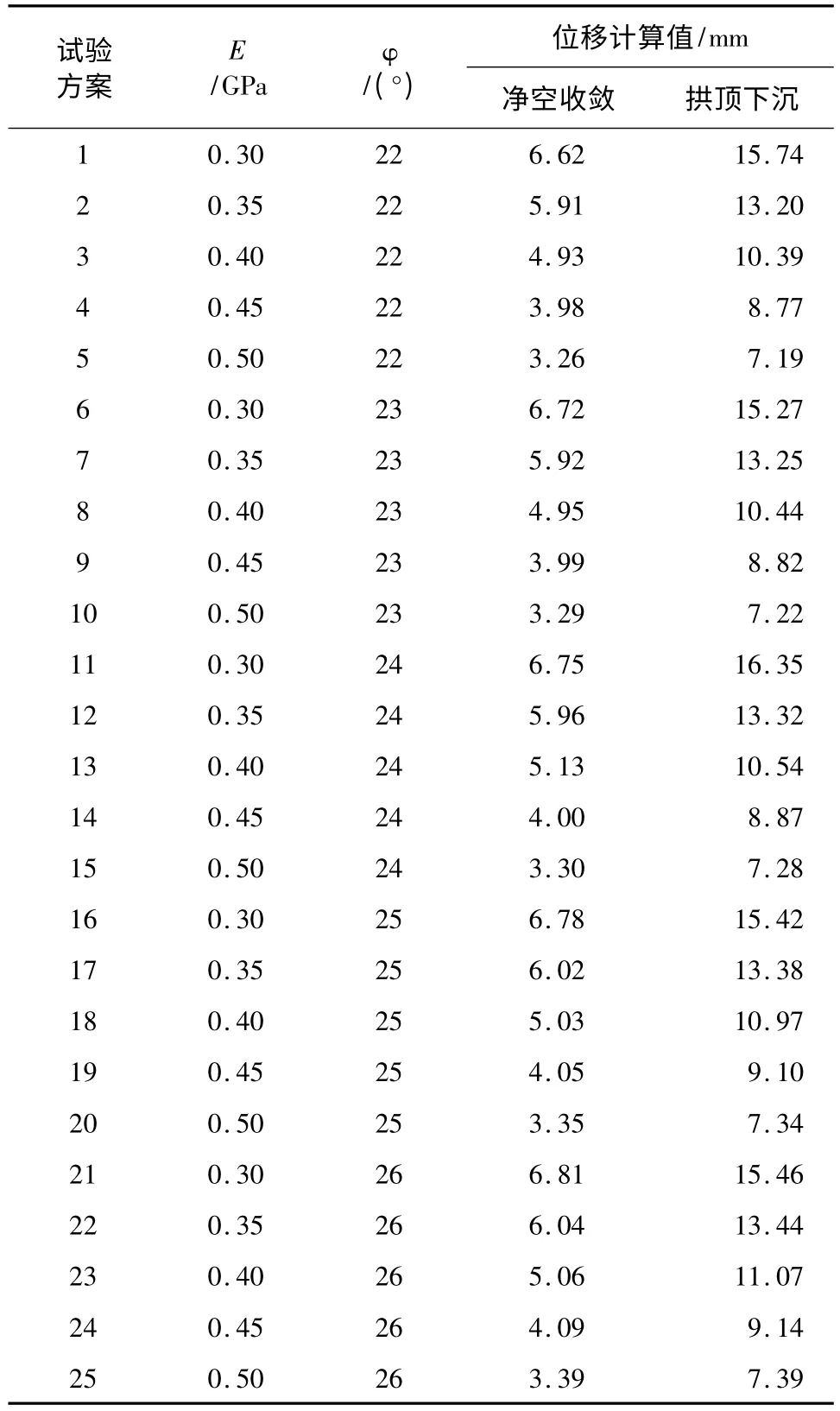
表4 神经网络训练样本

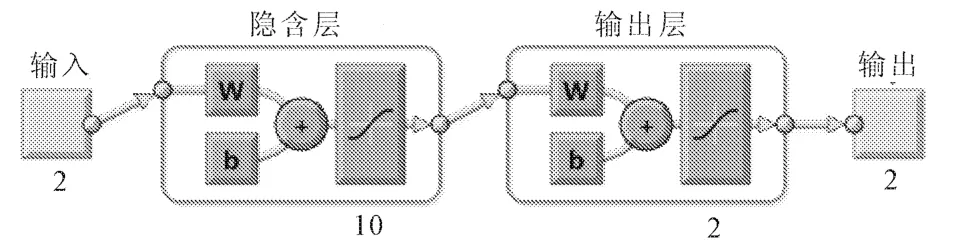
图5 神经网络模型结构图

4.3 网络训练及效果评价

学习样本中各参数具有不同的物理意义和变化范围，为了使各个输入量在网络训练中具有同等重要的位置，减少网络学习的波动性，需要对样本中的各参数进行标准化处理[15]，本文采用 Mapminmax函数对学习样本进行标准化处理，使参数值分布在[0，1]之间。用标准化处理后的学习样本进行网络的训练，得到相关训练误差曲线如图6所示。神经网络误差记录图6中可以看到误差曲线刚开始的收敛速度较快，后趋于平缓，在训练进行到第363次时训练误差趋近于设定误差，300次时性能检验最好，找到有效的最优化结果。

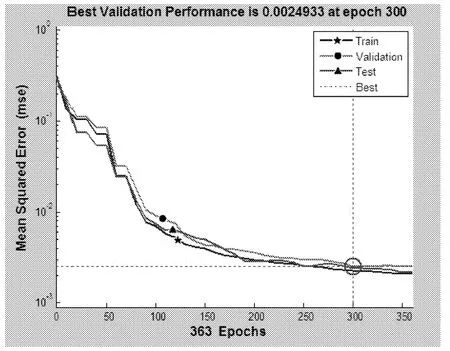
图6 训练误差曲线

5 智能位移反分析系统在长春地铁的应用

选取监测断面ZDB570的拱顶下沉值为17.02 mm，净空收敛值为6.16 mm，将这组位移的参数组合代入到建立的BP神经网络模型中，进行仿真，得到隧道围岩参数弹性模量E=0.33 GPa，内摩擦角φ=22.8°。将反分析得到的围岩力学参数E，内摩擦角φ，同其他已知的岩土参数(重度、黏聚力、侧压力系数、泊松比等)代入到三维数值分析模型中进行求解，得到典型断面ZDB570处的仿真模拟位移值(拱顶下沉和净空收敛)，并与实测值进行比较，见表5。

表5 仿真结果表

由表5可知，拱顶下沉和净空收敛的仿真位移值与实测值相比较，相对误差分别为4.7%、12.3%，净空收敛位移值的相对误差相对较大，但都符合反分析结果相对误差20%的检验标准。而且仿真模拟得到的位移值偏大，这对工程施工来说是有利的。因此，利用本文所采用的基于BP神经网络的智能位移反分析方法求得的岩体力学参数进行数值模拟和计算时，满足理论研究和工程实际的需求。

通过暗挖区间施工模拟，提取断面ZDB570处的位移云图如图7、图8所示。

其中，水平方向位移沿隧道中轴线呈左右对称分布，整个断面水平方向呈向内挤压的状态，水平方向围岩最大位移发生在拱脚部位[16]，其次是拱腰部位，拱顶、拱底部位由于围岩的水平对称作用，水平位移最小。由于考虑了超前小导管注浆加固，断面上部位置的水平位移值较小，对于拱脚处较大的水平位移，施工中应及时打设锁脚锚杆，钢拱架及时封闭成环。竖向位移云图中地层变形延伸至地表，最大围岩位移出现在拱顶、拱底部位，其次是拱腰、拱脚部位。这都与工程实际监测情况是相吻合的。验证了通过运用本文所采用的智能位移反分析方法求得的参数值在数值模拟中运用的有效性。

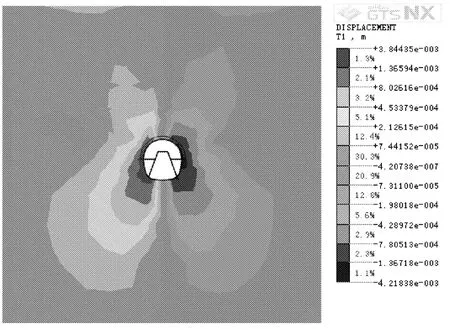
图7 水平位移场云图

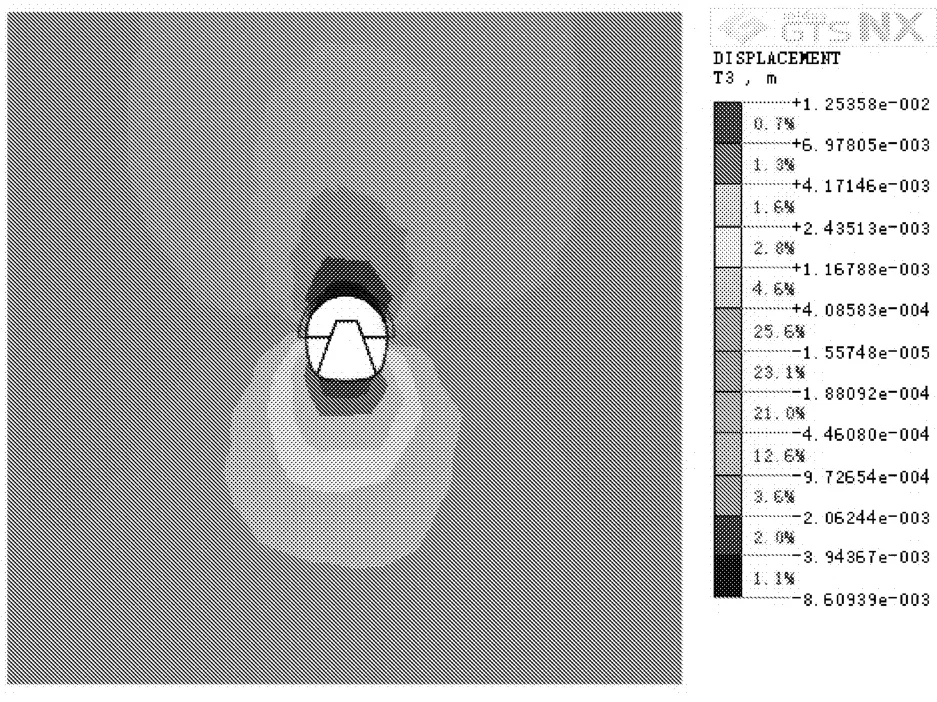
图8 竖向位移云图

6 结论

(1)运用敏感性分析得到了所研究工程区域内对围岩变形影响最大的岩土体力学参数为弹性模量和内摩擦角。

(2)以现场监测的位移值为依据，运用数值模拟正算模型、BP神经网络模型所建立的智能位移反分析系统所求得的岩土体参数，在数值模拟分析中，求得的位移值更加符合工程实际。对于地表变形的计算、该地区其他工程数值模拟分析中参数的选取、隧道围岩变形控制及工程设计、施工及参数优化等有一定的参考价值和指导意义。

(3)本文所建立的智能位移反分析系统，只适用于该工程区域或相同地质条件下围岩参数的反分析，随着智能技术的发展及理论研究的深入，建立应用性更强、适用范围更广的智能位移反分析系统是未来智能位移反分析研究的发展方向。

参考文献:

[1]刁心宏，王泳嘉，冯夏庭.用人工神经网络方法辨识岩体力学参数[J].东北大学学报:自然科学版，2002，23(1):60-63.

[2]刘志宝，宁海龙，张海涛.岩土工程中位移反分析方法及其进展[J].路基工程，2016(5):7-9.

[3]冯夏庭，张志强，等.位移反分析的进化神经网络方法研究[J].岩石力学与工程学报，1999，18(5):529-533.

[4]Sotirios S Vardakos，Marte S Gutierrez，Nick R. Back-analysis of Shimizu Tunnel No.3 by distinct element modeling[J]. Tunnelling and Underground Space Technology，2007(22):401-413.

[5]Midas GTS 03 Analysis Reference[M].北京:北京迈达斯技术有限公司，2007.

[6]冯夏庭.智能岩石力学导论[M].北京:科学出版社，2000.

[7]黄书岭，冯夏庭，张传庆.岩体力学参数的敏感性综合评价分析方法研究[J].岩石力学与工程学报，2008，27(1):2624-2630.

[8]张志华，周传波，夏志强，等.地铁隧道土体参数敏感性分析与正交反演[J].中南大学学报:自然科学版，2013，44(6):2488-2493.

[9]章 光，朱维申.参数敏感性分析与试验方案优化[J].岩土力学，1993，14(1):51-57.

[10]方 正，吴 平，刘丹珠.软土隧道岩体参数正交反演分析[J].现代隧道技术，2013，50(2):66-71.

[11]方开泰，马长兴.正交与均匀试验设计[M].北京:科学出版社，2000.

[12]方开泰.均匀设计与均匀设计表[M].北京:科学出版社，1994.

[13]黄修云，曹国安，张 清.人工神经网络在地下工程程预测中的应用[J].北方交通大学学报，1998，22(1):39-43.

[14]李 丽，王振领.MATLAB工程计算及应用[M].北京:人民邮电出版社，2001.

[15]丛 爽.面向Matlab工具箱的神经网络理论与应用[M].合肥:中国科学技术大学出版社，2003.

[16]丁录董.基于数值模拟的隧道开挖及支护方法选择[J].勘察科学技术，2012(3):9-12.