四点剪切条件下岩石-混凝土界面裂缝扩展过程研究
2015-12-21何佳文
陆 超,何佳文,2,董 伟
(1.大连理工大学 海岸与近海工程国家重点实验室,辽宁 大连116024;2.沈阳鼎伦装饰工程有限公司,辽宁 沈阳110015)
建立在岩石基础上的混凝土结构物,岩石与混凝土的交界面是一个薄弱环节,由于材料的非均质、结构物所受外力的随机性以及自然环境的影响使得界面裂缝的断裂问题具有一定的复杂性[1-3]。许多学者针对这一问题进行了深入的研究,Lee[4]用三明治试件得到了砂浆与粗骨料界面的断裂韧度曲线,并研究了模态比与断裂韧度的关系。Buyukozturk[5]利用三点弯曲梁试件进行研究,发现界面断裂韧度依赖于骨料与砂浆的弹性模量和各自的断裂韧度。黄松梅[6]、李哲[7]、杨水成[8]用单边切口梁研究了岩石与混凝土界面裂缝扩展曲线,提出了二维与三维界面裂缝的断裂准则。Yang[9]采用四点剪切梁研究了不同加载形式下模态比对岩石与混凝土界面裂缝断裂韧度的影响,并拟合出了抛物线型和椭圆型两种界面破坏准则。
以上的成果极大地促进了界面裂缝断裂性能的研究,然而,这些研究更关注于裂缝的起裂及失稳状态的判断,没有将裂缝的走向和扩展的不同模式作为研究目标。对于实际的结构物,处于岩石-混凝土界面中的裂缝在不同应力场的影响下除沿界面扩展外还会发生向岩石扩展的模式。扩展路径的变化会引起裂缝所处两侧材料属性、裂缝尖端应力场和虚拟裂缝长度范围内粘聚力的变化等诸多问题,因此研究界面裂缝的扩展过程并对裂缝可能发生的扩展模式进行预测就显得尤为重要[10]。Volker Slowik等[11]最早以混凝土重力坝为工程背景研究了岩石-混凝土界面断裂问题,认为大坝坝底起源于界面的裂缝易向基岩扩展。在此基础上,Volker Slowik等[12]在Hillerborg模型基础上推导出复合型加载模式下的应力强度因子计算方法并提出了相应的裂缝扩展准则,然而其模拟出的界面裂缝沿界面扩展,没有出现扩展一段后转向岩石的扩展模式,另外其采用高强度混凝土来模拟基岩并不能反应岩石材料本身的特性,因此还应该再加以补充。钟红等[13-14]采用四点剪切试件进行了岩石与混凝土界面裂缝在复合型应力场下的断裂特性研究,发现岩石混凝土界面随着偏缝率和模态比的不同其破坏主要呈现二种形式:沿界面扩展和向岩石扩展。在其研究范围内,探讨了裂缝沿界面扩展的全过程,但未对裂缝可能出现的向岩石扩展情况进行判断及研究。
综上所述,目前对于界面裂缝的扩展研究主要集中于在裂缝沿两种材料交界面的扩展分析,在此基础之上再开展相关界面断裂特性及扩展过程的分析,尚缺乏一个有效的准则对于裂缝扩展过程中可能出现的偏离界面向一侧材料发展的情况进行判定。基于此,本文首先采用试验方法研究了四点剪切加载条件下界面裂缝在不同加载方式、缝高比、偏缝率下的裂缝扩展轨迹,并依据试验结果将裂缝的扩展模式分成两种类型:沿界面扩展(I)和向岩石扩展(R)。进而提出了以起裂断裂韧度为参数的裂缝扩展准则,用于判断界面裂缝在Ⅰ-Ⅱ复合型应力场下可能出现的扩展模式。采用ANSYS有限元分析软件对岩石-混凝土四点剪切梁断裂过程进行数值模拟,计算了裂缝不同扩展模式下完整断裂过程,并获取相关断裂参数,最后通过与试验结果的对比验证了本文所提出准则的正确性。
1 试验研究
1.1 试件准备
本次试验采用100 mm×100 mm×500 mm的梁式试件,一侧为岩石,另一侧为混凝土。混凝土配合比如表1所示,其中所用水泥为P42.5普通硅酸盐水泥,骨料最大粒径为10 mm。表2列出了岩石和混凝土的各项力学参数。

表1 混凝土配合比

表2 材料力学性能参数
为了模拟岩石的自然断面,本文参考了Hassanzadeh[15]研究岩石断裂性能时采用的方法,首先按照试验设计初始逢高比对岩石进行预制缝的切割制作,然后采用三点弯加载的方式使岩石从预制裂缝处断裂,得到垂直于长轴的断面。折断后的岩石在预制裂缝面位置用减摩片和胶纸粘贴以隔离其表面与浇筑混凝土的粘结,岩石三点弯曲试验如图1所示。

图1 岩石自然断面的获取
1.2 试验方案
本次试验采用图2所示四点剪切的加载方式,为了得到裂缝扩展的不同模式,对加载方式、缝高比和偏缝率进行了变量控制,分别为加载点距离比L1∶ L2=4、6、10,偏缝率 C1=5 mm、10 mm、15 mm,缝高比 a0/D=0.2、0.3、0.4、0.5、0.6。试件编号按照上述三种变量的先后顺序组成,如“L4-5-20”表示 L1∶ L2=4,C1=5 mm,a0=20 mm 的工况。不同组合下的工况有45种,每种工况下3个试件,共计135个四点剪切梁试件。另外,为计算界面断裂参数,制作5种缝高比下的三点弯曲梁各三个,总计15个三点弯曲梁试件。由于实际工程中,在库水压力等外部荷载作用下,坝体与基岩交界面处的裂缝通常处于Ⅰ-Ⅱ复合型应力场作用下,这就使得交界面处的裂缝沿界面扩展或者偏向坝基岩体扩展,而不会出现向上部坝体混凝土扩展的情况。因而本文的试验设计也考虑了这一因素,在图2的加载方案中,裂缝不会出现向混凝土扩展的情况。

图2 四点剪切加载(单位:mm)
三点弯曲梁试验在25 t微机控制电液伺服万能材料试验机(MTS)上进行,主要目的是测定荷载及位移量,包括起裂荷载、最大荷载、裂缝口张开位移、加载点挠度,进而计算得到界面的断裂能、起裂断裂韧度及失稳断裂韧度。数据由德国进口的IMC数据采集系统采集。采用夹式引伸仪测量加载点处的挠度δ。在梁的两侧预制裂缝的尖端位置对称粘贴四个应变片来监测缝尖应变在加载过程中的变化。如图3所示,起裂时应变将出现回滞现象,图3中最大应变所对应的荷载值即为起裂荷载。四点剪切试验在相同的试验机上进行,根据前述的不同工况进行了系统的试验,测量了起裂荷载、最大荷载、裂缝口张开位移、裂缝口滑开位移、加载点挠度,同时得到裂缝扩展的三种模式。试验采用位移模式控制,加载速度为0.012 mm/min。

图3 裂缝尖端应变回滞现象
2 试验结果与分析
2.1 三点弯曲梁试验
由于三点弯曲梁自身的特点,在不同缝高比下所有试件的破坏模式都是沿界面扩展,15个试件中有12个采集到了完整的加载点挠度(P-δ)曲线。用应变片测得起裂荷载 Pini后,结合不同工况下的缝高比,基于界面断裂力学方法计算不同工况下的起裂韧度用断裂功法计算了各种工况下的界面断裂能,每种工况下的三点弯曲梁试验结果均值列于表3。

表3 三点弯曲梁试验及计算结果
根据表3所示结果,不同缝高比下 Pini/Pmax的均值集中于0.75~0.91之间,基本不受缝高比的影响;基本不随缝高比的变化而变化,其与缝高比的相关系数仅为0.072,而且界面应力强度因子的Ⅱ型分量趋近于0,其破坏模式可以近似认为纯Ⅰ型断裂。可以认为岩石-混凝土界面的起裂韧度可以作为界面的材料参数使用,在后续计算中取其平均值,即界面Ⅰ型起裂韧度=0.364 MPa·m1/2,界面Ⅰ型断裂能 GItf=21.901 N/m,岩石起裂韧度=1.087 MPa·m1/2,岩石断裂能 GRf=119.69 N/m。
2.2 四点剪切梁试验
四点剪切梁的破坏过程都比较短促,在达到最大荷载后裂缝很快扩展直至完全破坏。裂缝扩展模
式可分为全过程沿界面扩展(I)和向岩石扩展(R)两种情况。两种典型的裂缝扩展模式见图4。

图4 两种裂缝扩展模式
根据界面力学理论,界面裂缝的断裂行为跟应力强度因子比值K2/K1也即模态比有关[16],图5给出了不同工况下K2/K1的变化,可以看出:不同工况下,随着缝高比的增加,K2/K1均呈现先增大后减小的趋势;相同缝高比下,L1∶L2越大、C1越小,则K2/K1越大。结合试验中两种扩展模式,将图5划分为I、R两个区域,从试验结果统计中可以看出,位于R区域的试件倾向于向岩石扩展,位于I区域的试件全部沿界面扩展。当L1:L2=4时,I区域与R区域的分界线在 K2/K1=1.38附近;当 L1:L2=6时,I区域与R区域的分界线在K2/K1=1.26附近;当L1:L2=10时,I区域与R区域的分界线在K2/K1=1.58附近;三种工况下I区域与R区域的分界线平均值为K2/K1=1.4。由于模态比 K2/K1消除了荷载大小的影响,是一个与加载方式、材料属性和裂缝位置有关的常数,因此可以认为,当岩石混凝土界面裂缝模态比K2/K1大于1.4时,裂缝在扩展过程中将会向岩石扩展。

图5 不同工况下K2/K1的变化
3 数值计算
3.1 界面裂缝扩展准则
由于界面两侧材料的差异性,传统的单一材料下的断裂准则不再适用于判断界面裂缝的发展,对于界面裂缝的断裂准则,在其他材料中发展较早,如Yuuki[17]基于最大切线应力理论提出了曲折破坏准则并采用铝-环氧树脂制作的圆盘形试件进行了验证[18],Toru Ikeda[19]制作含有不同形式初始裂缝的试件计算了界面裂缝的应力强度因子,并总结了用应力强度因子表示的破坏准则。对于岩石-混凝土界面的断裂准则,国内外的研究比较少。黄松梅等[6]用四点剪切梁试件进行岩石 -混凝土界面断裂性能研究,计算出断裂曲线,证明其与最大拉应力准则及最大拉应变准则比较吻合,然而当荷载最大时,裂缝已有很长的稳定扩展,采用初始缝长确定的断裂曲线存在一定的误差。研究表明,裂缝失稳前存在稳定扩展阶段,根据虚似裂缝模型[20],试件除了受外荷载P作用外,还存在阻止裂缝扩展的黏聚力σ(w)作用,根据叠加原理,可将图6(a)分解为图6(b)和图6(c),他们的应力强度因子有如下关系:

式中:KP1,2是由荷载 P产生的应力强度因子;Kσ1,2是由黏聚力σ(w)产生的应力强度因子。

图6 叠加法计算 K1,2
本文采用董伟等[21]提出的岩石-混凝土双线型软化本构曲线来施加界面段黏聚力。由于岩石脆性较强,本文认为裂缝在岩石的扩展段没有黏聚力作用。当裂缝沿界面扩展时,采用界面断裂力学计算界面应力强度因子;当裂缝扩展到单一材料时,采用ANSYS自带的位移外推法计算裂缝尖端应力强度因子。
裂缝扩展过程中,每一步扩展都经历了荷载从零增长,达到起裂条件使裂缝开始扩展这一过程,即每一步都经历了裂缝起裂和稳定扩展阶段[22-23]。界面裂缝扩展准则总结如表4所示。

表4 岩石-混凝土界面裂缝扩展准则
3.2 计算结果及分析
根据试验结果可知,岩石-混凝土界面裂缝扩展可分为两种模态,即:沿界面扩展(I)和向岩石扩展(R),下面从每种扩展模态选出两种工况进行数值结果与试验结果的对比,详细结果列于表5。从表5可知,起裂荷载Pini、最大荷载Pmax的计算结果与试验结果吻合较好。
图7为试件L6-5-50b裂缝扩展全过程。由于在数值计算过程中,裂缝每一步扩展一个人为设定的增量Δa,然后重新建模划分网格进行计算,最终计算过程的结束是以荷载下降到零为标准,因此数值模拟结果中裂缝并未完全扩展到梁的边界而模拟过程已经结束,因而图7中显示的裂缝扩展轨迹并未贯通整个试件。图8为裂缝扩展轨迹对比,可知数值计算的裂缝扩展轨迹与试验所得到的扩展路径吻合较好。图9为 P-Scmod曲线与 P-Scmsd曲线对比,由于试验机刚度、岩石-混凝土界面粘结强度较低以及岩石的准脆性等原因,试验中未能测到P-Scmod曲线与P-Scmsd曲线的下降段,从图中可以看出,沿界面扩展模式下试验与数值结果的荷载吻合良好,向岩石扩展的模式下数值计算荷载比试验荷载偏大,这是由于向岩石扩展下,初始裂缝却处于界面位置,界面的抗拉强度低于岩石的抗拉强度,从界面到岩石会引起材料属性和裂缝尖端应力的变化,因而会出现上述结果。两种扩展模式下裂缝口张开位移的试验值都要比数值计算结果偏大,这是由于数值计算中采用节点相对位移来计算裂缝口张开位移,而试验采用粘贴在试件底部的小钢片固定夹式引伸仪来测定,严格来讲试验中测得的是裂缝口下端小钢片厚度处的张开位移,因而会比数值计算结果偏大。

表5 数值计算结果与试验结果的比较
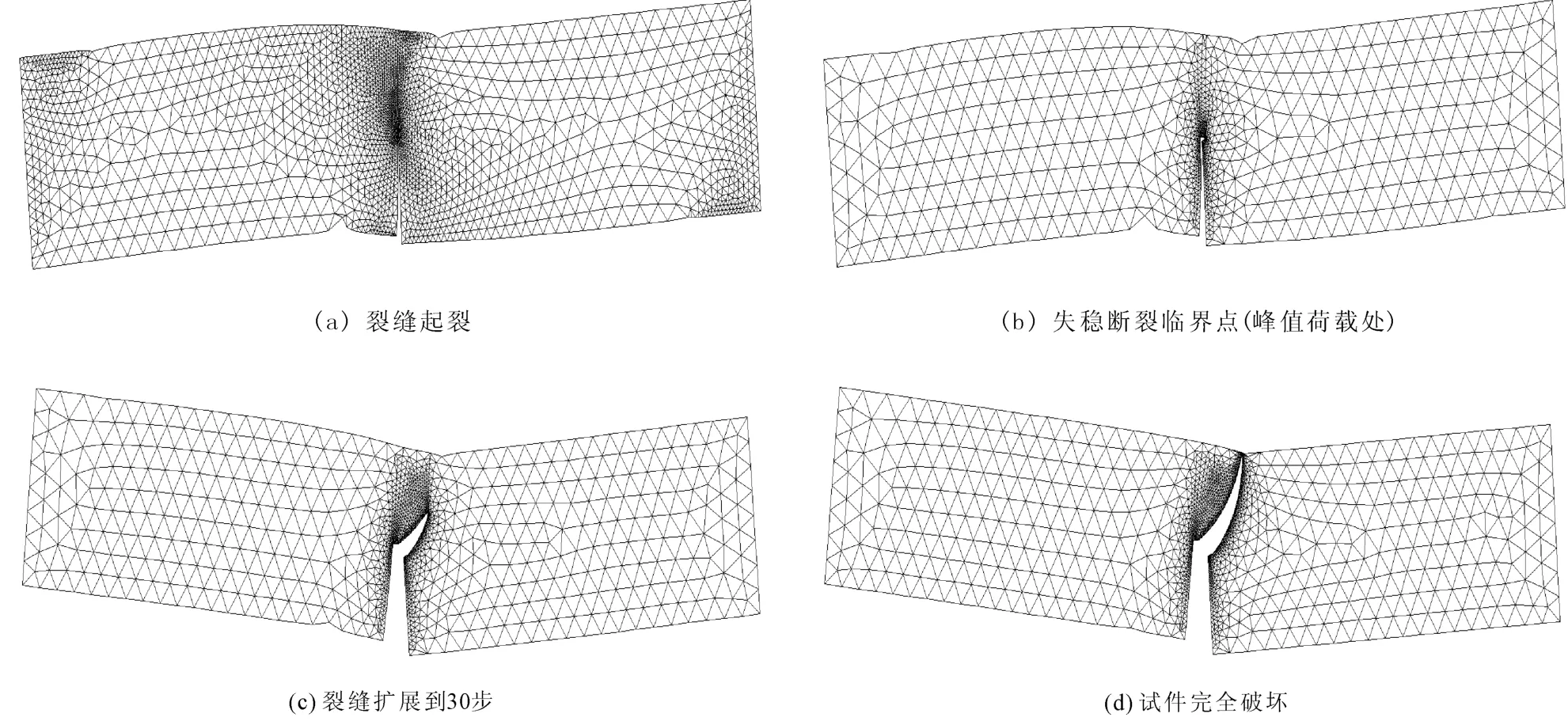
图7 试件L6-5-50b裂缝扩展全过程
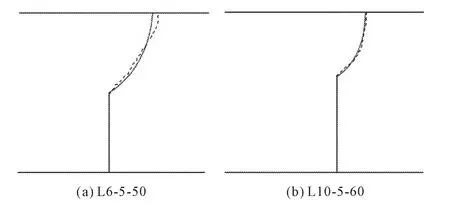
图8 裂缝扩展轨迹对比(虚线为试验结果,实线为数值结果)

图9 P-Scmod曲线对比
4 结论
本文对不同工况下的岩石-混凝土界面四点剪切梁进行了试验研究和数值计算,研究了不同加载方式、偏缝率和逢高比下岩石-混凝土界面裂缝扩展的三种模态,可以得到如下结论:(1)不同工况下,岩石-混凝土界面裂缝的扩展存在两种模态:沿界面扩展和向岩石扩展;(2)应用本文提出的界面裂缝扩展准则并结合有限元数值计算得到的裂缝扩展路径、起裂荷载、最大荷载以及P-Scmod曲线与 P-Scmsd曲线与试验结果吻合良好;(3)应用本文所提出的方法,只要从试验中得到界面、混凝土与岩石的基本力学参数如抗拉强度、弹性模量、泊松比和断裂参数如断裂能和起裂断裂韧度,即可计算岩石-混凝土界面Ⅰ-Ⅱ复合型裂缝扩展全过程,分析裂缝扩展的不同模式,求解起裂荷载、极限荷载、裂缝扩展长度等断裂参数。
[1]郭胜山,陈厚群,李德玉,等.重力坝与坝基体系地震损伤破坏分析[J].水利学报,2013,44(11):1352-1358.
[2]黄松梅,王冬玲,李 哲,等.拱坝的开裂计算[J].西安理工大学学报,1998,14(1):18-23.
[3]杨 强,陈英儒,刘耀儒.基于变形加固理论的高拱坝坝踵开裂分析[J].水利学报,2008,39(1):20-26.
[4]Lee K M,Buyukozturk O.Fracture analysis of mortar-aggregate interfaces in concrete[J]. Journal of Engineering Mechanics,1992,118:2031-2047.
[5]Buyukozturk O,Hearing B. Crack propagation in concrete composites influenced by interface fracture parameters[J]. International Journal of Solids and Structures,1998,35:4055-4066.
[6]黄松梅,简 政,马素菁,等.混凝土异弹模界面裂缝断裂准则的试验研究[J].水利学报,1994,25(6):74-79.
[7]李 哲,刘茂社,张建山,等.岩石与混凝土界面裂缝断裂准则及断裂能的试验研究[J].陕西水力发电,2001,17(4):35-37.
[8]杨水成,黄松梅,宋 俐,等.岩石与混凝土三维界面裂缝断裂准则的试验研究[J].水利学报,2002,33(10):107-112.
[9]Yang S C,Li S,Li Z,et al. Experimental investigation on fracture toughness of interface crack for rock/concrete[J]. International Journal of Modern Physics B,2008,22:6141-6148.
[10]柏承新,赵代深.应用二次奇性边界元分析重力坝坝踵裂缝的开展[J].土木工程学报,1988(2):1-21.
[11]Volker Slowik,Chandra K J M,Saouma V E. Mixed mode fracture of cementitous biomaterial interfaces;Part I:experimental results[J]. Engineering Fracture Mechanics,1998,60(1):83-94.
[12]Volker Slowik,Chandra K J M,Saouma V E. Mixed mode fracture of cementitous biomaterial interfaces;PartⅡ:numerical simulation[J]. Engineering Fracture Mechanics,1998,60(1):95-107.
[13]Hong Zhong,Ean Tat Ooi,Chongmin Song,et al. Experimental and numerical study of the dependency of interface fracture in concrete—rock specimens on mode mixity[J]. Engineering Fracture Mechanics,2014,124:287-309.
[14]丁 涛,钟 红,林 皋.岩石与混凝土界面断裂特性的试验研究[J].水利与建筑工程学报,2013,11(5):118-199.
[15]Hassanzadeh M. Fracture mechanical properties of rocks and mortar/rock interfaces[C]//MRS Proceedings.Cambridge University Press,1994.
[16]Hutchinson J W,Suo Z.Mixed mode cracking in layered materials[J]. Advances Applied Mechanics,1992,29:63-191.
[17]Yuuki R,Xu J Q.Stress based criterion for an interface crack kinking out of the interface in dissimilar materials[J]. Engineering Fracture Mechanics,1992,41(5):635-644.
[18]Yuuki R,Liu J Q,Xu J Q.Mixed mode fracture criteria for an interface crack[J]. Engineering Fracture Mechanics,1994,47(3):367-377.
[19]Toru ikeda,Noriyuki miyazaki. Mixed mode fracture criterion of interface crack between dissimilar materials[J]. Engineering Fracture Mechanics,1998,59(6):725-735.
[20]Hillerborg A,Modeer M,Petersson P E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J]. Cement and Concrete Research,1976(6):773-782.
[21]董 伟,张利花,吴智敏.岩石 -混凝土界面拉伸软化本构关系试验研究[J].水利学报,2014,45(6):712-719.
[22]吴智敏,董 伟,刘 康,等.混凝土Ⅰ裂缝扩展准则及裂缝扩展全过程的数值模拟[J].水利学报,2007,38(12):1453-1459.
[23]吴智敏,董 伟,许 青.混凝土Ⅰ -Ⅱ复合型裂缝扩展准则及扩展全过程的数值模拟[J].水利学报,2009,40(2):180-187.
[24]Erdogan F,Sih G C. On the crack extension in plates under plane loading and transverse shear[J]. Basic Engineering,1963,85(4):519-525.
