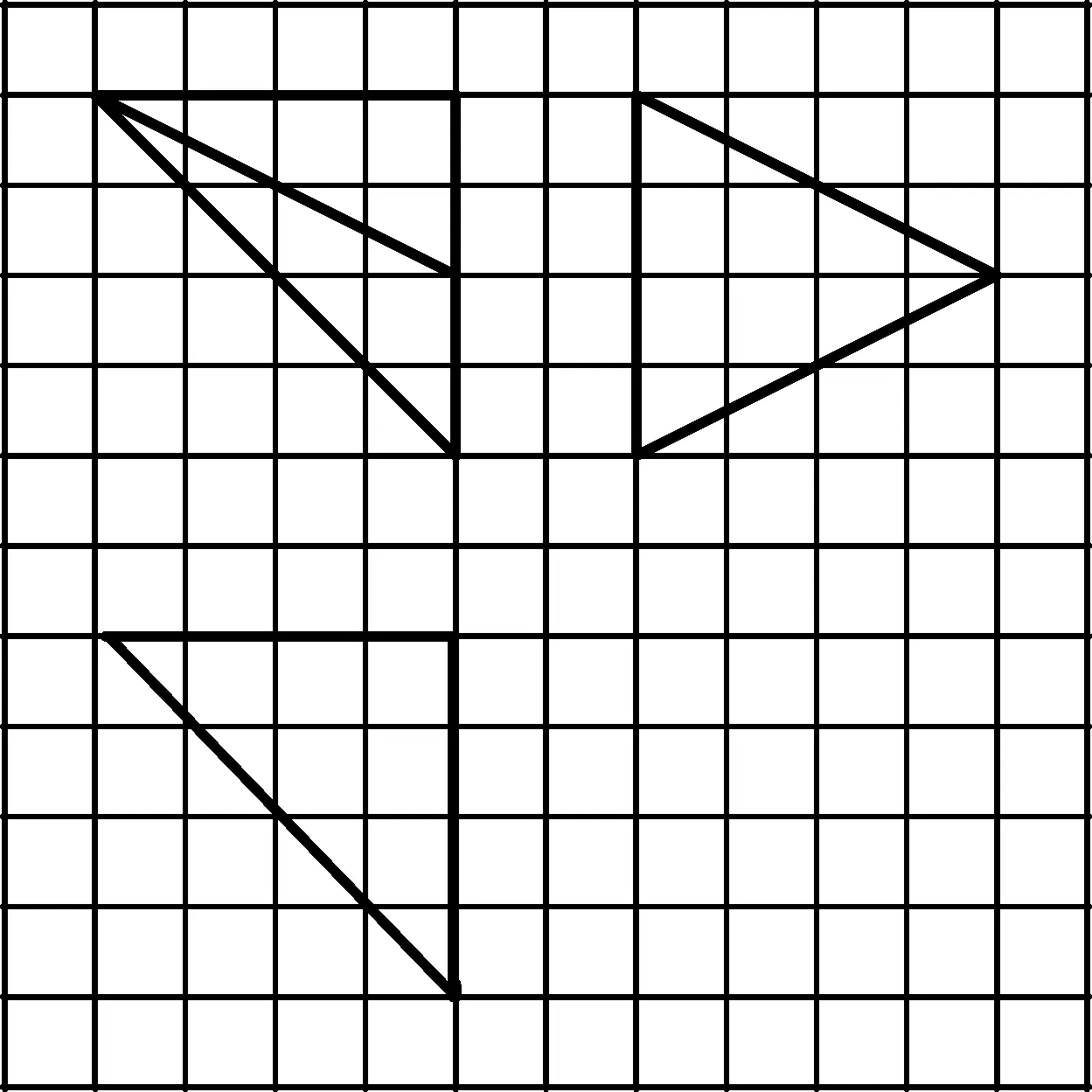
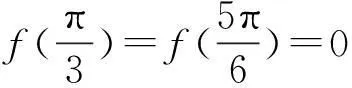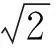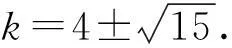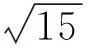高考改革与数学高效复习策略

高考改革与数学高效复习策略

苗金利

(北京市第四中学，北京100088)

党的十八大以来，新一轮的高考改革正在逐步落实，继《义务教育数学课程标准(2011年版)》的颁布之后，高中新的课程标准制定即将完成，高考制度的改革逐步深入，2014年底以来教育部出台了系列高考及高校招生(含各高校自主招生方法)改革指导文件，包括今年将增加3个省份在高考中使用国家统一试卷,明年再扩大7个省份．届时，将有25个省份在高考中使用由国家考试中心统一命题制作的试卷．

最近颁布的2015年全国统一高考《数学考试大纲》，规定数学学科高考考查中学数学的基础知识、基本技能、基本思想方法，考查空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力以及分析问题和解决问题的能力．重视知识发生发展的过程考查，强化运算过程、运算结果的重要性，强化数学应用能力的考查．考查要求数学学科要注重基本的数学能力、数学素养和学习潜能的考查； 突出主干知识，考查基本的数学思想、方法，强调通性通法，淡化特殊技巧；注意数学应用，考查学生利用数学概念、原理和方法，结合数据分析、图像解析等内容，解释现实世界中的现象，解决生产生活中的数学问题．

高考《数学考试大纲》确立，数学试卷由容易题、中等难度题和难题组成．结合《普通高中数学课程标准(实验)》，从高考题目的简单容易题、中档综合题、高难“数学”题所占比例是3∶5∶2．从中学数学知识、方法、能力、操作来讲基础性、综合性和抽象拓展性在试卷中所占比例也是3∶5∶2．

作为高考指导教师要注重教育培养学生能以平和的心态参加考试，不要把高考数学妖魔化．同时，考试中合理支配考试时间，以实事求是的科学态度解答试题，树立战胜困难的信心，体现锲而不舍的精神．教学中要讲“数学”：提炼数学最本质的精髓，形成知识网络架构，答题目标是：3分基础，一分不丢；重“认知”：经典问题洞察题眼，分析解法，熟练掌握知识内容，答题目标是：5分综合，分分必得；求“发展”：例题习题后面要举一反三，拓展反思，灵活应对各类型知识和题目的考查，答题目标是：2分拓展，分步得分，力争全拿．

针对高考改革和高考数学试题新的特点，高三指导教师对2015年高考数学试卷的结构、考试的内容及要求等方面也应有宏观的认识，同时在高三后期复习中要特别关注以下几个方面：

1.高考的指导思想和目标

注重考查中学数学的基础知识、基本技能、基本操作、基本思想方法．重视考生的“终身学习和发展”，即考查学生在中学所受到的数学教育，考查学生在大学需要的数学基础能力．试卷力争成为学生能够展示自己风采的舞台．

2.试题“稳中有新”，凸显课程改革理念的精髓

2015年高考数学试题，会在过去两年数学试题改革的基础上，在很大程度继续让我们感受到课程改革的气息，新课程的理念和评价思路渗透在试题中，考查目标更是与新课程的教学要求有比较紧密的体现，能够让人明显感觉到高考与课标要求之间的对接与配合，试题体现出稳定之中有新意、有亮点、有变化的共同特点．

在知识与能力、过程与方法及情感态度价值观等不同维度的考查上，全国各命题单位组都在寻求新思路、新视角以及新的呈现形式方面下功夫．数学学科的试题均会有“新味”．

在平时备考过程中应多联系生活、联系生产、联系科技，联系社会，体现“学以致用”的新课程价值观．

例1(2014北京理8)学生的语文、数学成绩均被评定为三个等级，依次为“优秀” “合格”“不合格”．若学生甲的语文、数学成绩都不低于学生乙，且其中至少有一门成绩高于乙，则称“学生甲比学生乙成绩好”．如果一组学生中没有哪位学生比另一位学生成绩好，并且不存在语文成绩相同、数学成绩也相同的两位学生，那么这组学生最多有()．

A．2人B．3人C．4人D．5人

解：法一：逻辑映射

甲乙丙012

两两相交(不能有平行，否则出现“高于”)

唯一连法，再多时，无法连接．

故选B．

法二：数独

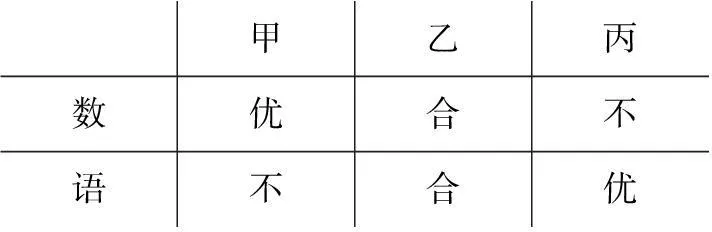
甲乙丙数优合不语不合优

例2(2014全国Ⅰ卷理14)甲、乙、丙三位同学被问到是否去过A，B，C三个城市时，

甲说：我去过的城市比乙多，但没去过B城市；

乙说：我没去过C城市；

丙说：我们三人去过同一个城市．

由此可判断乙去过的城市为().

解：A

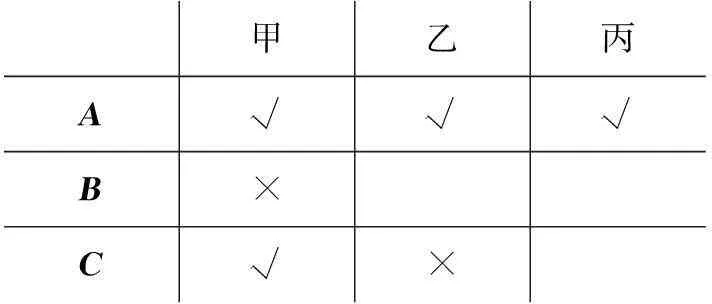
甲乙丙A√√√B×C√×

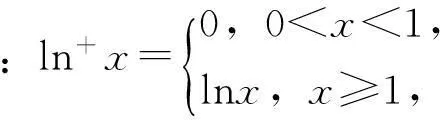
①若a>0,b>0，则ln+(ab)=bln+a；

②若a>0,b>0，则ln+(ab)=ln+a+ln+b；

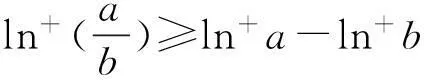
④若a>0,b>0，则ln+(a+b)≤ln+a+ln+b+ln2．

其中的真命题有__________.(写出所有真命题的编号)

解析：

①若a>0,b>0，则ln+(ab)=bln+a；

当a≥1,b>0,ab≥1⟹ln+ab=lnab=blna=bln+a；

当00,0

所以①正确．

②若a>0,b>0，则ln+(ab)=ln+a+ln+b．

由于∃ab<1,a>1,0

所以②错误．

同理可以判定③④正确．

答案①③④．

3.基础知识、基本方法、基本操作、基本思想方法的运用仍为2015年高考考查的立足点

数学试题整体上从选材、设问到答案，既具有人文性、教育性、开放性的一面，同时又十分关注学科素养的考查．数学运算水平与数学的实际应用水平是数学学科的主要素养水平的体现．

强调主干知识、重点知识考查的覆盖，理科确立了52个(文科41个)重要考点，强调基础知识理解运用中的迁移、转化和应变能力，强调文、理科数学运用能力的特点、差异以及一定程度上的跨学科综合运用能力，仍会成为各地特色的能力考查方式．

各命题单位数学试题会注重常规与朴素；命题人不以学生为敌，不再以分出层次为目的，刻意追求区分度，要让数学试卷成为学生展示自己才华的舞台．高考难度继续保持较低标准，当然这并不意味降低数学要求，而是对基础知识、基本方法、基本操作、基本思想方法的落实上要求更高，从学生考试丢分情况看，审题错误、操作失误、基本知识不落实三项丢分总和大约估计会占考生总丢分的40%以上，问题还是相当严重的。比如2014年高考，北京四中的朱子林同学，用一个小时答完全部试题，而此时大部分同考场考生刚刚开始答解答题第一个大题，答题慢的主要原因就是四基不落实，答题慢的后果是做不完题，结果是考试100分钟后就心慌意乱，不能踏实答卷．

例4(2014全国2卷理19)某地区2007年至2013年农村居民家庭纯收入y(单位：千元)的数据如下表：

年份2007200820092010201120122013年份代号t1234567人均纯收入y2.93.33.64.44.85.25.9

(Ⅰ)求y关于t的线性回归方程；

(Ⅱ)利用(Ⅰ)中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入．

所以

=0.5，

例5(2014北京理16)李明在10场篮球比赛中的投篮情况统计如下(假设各场比赛相互独立)：

场次投篮次数命中次数场次投篮次数命中次数主场12212客场1188主场21512客场21312主场3128客场3217主场4238客场41815主场52420客场52512

(Ⅰ)从上述比赛中随机选择一场，求李明在该场比赛中投篮命中率超过0.6的概率；

(Ⅱ)从上述比赛中随机选择一个主场和一个客场，求李明的投篮命中率一场超过0.6，一场不超过0.6的概率；

解(Ⅰ)根据投篮统计数据，在10场比赛中，李明投篮命中率超过0.6的场次有5场，分别是主场2，主场3，主场5，客场2，客场4．

所以在随机选择的一场比赛中，李明的投篮命中率超过0.6的概率是0.5．

(Ⅱ)设事件A为“在随机选择的一场主场比赛中李明的投篮命中率超过0.6”，

事件B为“在随机选择的一场客场比赛中李明的投篮命中率超过0.6”，

事件C为“在随机选择的一个主场和一个客场中，李明的投篮命中率一场超过0.6，一场不超过0.6”．

4.高考题目有的也许会超出考生预料，出现部分考生感觉“别扭”

改革在预料之中，数学卷有的命题单位改革的步伐稍大．当然，从知识、能力、方法及创新上也基本是学生能力范围之中的．

(Ⅰ)求sin∠BAD；

(Ⅱ)求BD，AC的长．

所以sin∠BAD=sin(∠ADC-∠B)

=sin∠ADCcosB-cos∠ADCsinB

(Ⅱ)在△ABD中，由正弦定理得

在△ABC中，由余弦定理得

AC2=AB2+BC2-2AB·BC·cosB

所以AC=7．

本题考查启示：几何性质(平面几何的外角定理)，基础知识的综合应用能力，克服单纯靠做题代替复习，忽略知识的提炼．

例7[2014北京理17(1)]如图，正方形AMDE的边长为2，B，C分别为AM，MD的中点．在五棱锥P-ABCDE中，F为棱PE的中点，平面ABF与棱PD，PC分别交于点G，H．

(Ⅰ)求证：AB∥FG；

(Ⅱ)若PA⊥底面ABCDE，且PA=AE，求直线BC与平面ABF所成角的大小，并求线段PH的长．

解：(Ⅰ)在正方形AMDE中，因为B是AM的中点，所以AB∥DE．

又因为AB⊄平面PDE，

所以AB∥平面PDE．

因为AB⊂平面ABF，且平面ABF∩平面PDE=FG，所以AB∥FG．

(Ⅱ)因为PA⊥底面ABCDE，所以PA⊥AB，PA⊥AE．

如图建立空间直角坐标系Axyz，

设平面ABF的法向量为n=(x，y，z)，则

令z=1，则y=-1．所以n=(0，-1，1)．

设直线BC与平面ABF所成角为α，则

设点H的坐标为(u，v，w)．

即(u，v，w-2)=2(2，1，-2)．所以u=2λ，v=λ，w=2-2λ．

部分考生习惯了空间向量，本题(1)不好确定坐标，不适宜用空间向量解答，使得部分考生耽搁了时间、影响了情绪．

现行课标立体几何的教学与考查理念是空间感知，强化运算．

5.按部就班，用数学最本源的知识、方法备考2015年高考

高考改革，循序渐进，数学题目只能部分体现高考发展的趋势， “考查考生的创新精神和潜质，增强试题的科学性、公平性和规范性”．在进一步处理好“知识与能力”考查的同时，适当加大“过程与方法”的考查力度，兼顾“情感、态度与价值观”的考查，强调了试卷的选拔和导向功能．

例8(2014北京文8)加工爆米花时，爆开且不煳的粒数的百分比称为“可食用率”．在特定条件下，可食用率p与加工时间t(单位：分)满足的函数关系p=at2+bt+c(a，b，c是常数)，下图记录了三次实验的数据．根据上述函数模型和实验数据，可以得到最佳加工时间为()．

A.3.50分B.3.75分

C.4.00分D.4.25分

解析：由题意将点坐标代入方程得

考查启示：思路不明确，按部就班就好．

考查启示：数形结合，按部就班观察得解．

例10(2014全国1理12)如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为()．

CD=4，

故选C．

考查启示：三视图的最本源方法是，在长方体中用“割除法”还原空间图形本来面目．

(Ⅰ)求椭圆的离心率；

(Ⅱ)设P为椭圆上异于其顶点的一点，以线段PB为直径的圆经过点F1，经过原点的直线l与该圆相切. 求直线的斜率.

x0+y0+c=0.

①

又因为点P在椭圆上，故

②

设直线l的斜率为k，依题意，直线l的方程为y=kx.

考查启示：本题主要考查椭圆的标准方程和几何性质、直线的方程、圆的方程等基础知识. 考查用代数方法研究圆锥曲线的性质这一解析几何的本质. 考查运算求解能力，以及用方程思想解决问题的能力.部分考生习惯了“过去”解析几何的直曲联立韦达定理，而近年更常见的是“按部就班”，落实基础知识，基本方法，淡化技巧．在2014年还有北京、浙江等命题单位的解析几何都是这一考查思路．

笔者建议2015届的高考指导教师，要关注平时练习中学生出现的基础问题，不能归纳为一时马虎粗心，要查找深层次的原因，上升到数学素养、情商的落实高度解决问题，查缺补漏，才能在高考中取得优异成绩．

2015年至2017年是全国大部分省市深化高考制度改革的过渡期，“和谐”稳定的高考命题是广大考生和命题中心及党和政府的共同心愿．所以2015年高考数学学科与近年比较有如下特点: 适度创新，稳步过渡；考查本源，发展思维；依纲靠本，注重四基．