基于乘客满意度的快慢车运行管理研究

唐润宇 高 原

基于乘客满意度的快慢车运行管理研究

唐润宇 高 原

以快慢车停站方式下的地铁运行为研究对象，分析快慢车方案对旅客出行、站务管理等方面的影响。以最大化乘客满意程度为目标构建线性规划模型，利用Cplex进行编程求解，得到快慢车运行方案。并将快慢车运行方案与普通列车运行方案进行比较，得出快慢车运行方案会减少乘客平均等待时间，从而提高乘客满意度的结论。

地铁；快慢车；乘客满意度；运行方案

0 导言

目前，我国地铁线路基本上采用传统的站站停车方案，运营组织形式简单，旅客无需换乘。但随着人们生活水平的提高，对日常出行提出了更高的要求。世界上少数国家已经开始采取快慢车的运行方案，比如纽约地铁率先采用快慢车的运行方案并取得了非常好的成效。在我国，北京地铁6号线已经具备快慢车开行的硬件条件，广州21号线也在筹备规划建设快慢车方案。随之而来的如何建设快慢线、选择大小站、设计运行图等问题变得日益重要。

1 方案概述

特殊停站方式有3种，分别是跨站停站方案、区域停站方案和快慢车停站方案。本文的研究对象为快慢车停站方案。

快慢车方案是指在地铁线路上开行两类交路的列车：普通的站站停列车和快速的跨站停列车。快速列车只在线路的主要客流集散站停车，在其他车站安排通过。

快慢车停站方案的制定需要综合考虑客流分析、通过能力、旅客出行时间等方面。客流的空间分布特征是判断停站方案是否合适的主要依据，当线路各站点的上、下车客流量分布不均衡时，采用快慢车方案是有利的。

常见的快慢车车站有以下4种轨道设置形式，其中X代表大站即快车越行站，L代表小站即普通慢车站。

（1）单向单线列车运行模式。如图1所示，单向单线是最基本的股道布设方式。所有车站只有2条股道，其上快慢车的运行相互影响，快车无法超过慢车行驶，只能以损失线路通过能力来保证列车间隔时间。

图1 单向单线列车运行模式图

（2）单向单线快车大站越行运行模式。如图2所示，该类线路在大站设有4条股道，快慢车可以同时在大站停靠，允许快车越行慢车，且便于乘客换乘，我国尝试引用快慢车方案的地铁线路多采用该种股道设置形式。

图2 单向单线快车大站越行运行模式图

（3）三股线路运行模式。如图3所示，三股线路在实际中较为少见，中间股道随客流高峰方向的不同而改变运营方向，客流高峰时使用2条股道承担客流较大方向的运营，采用快慢车独立运营，另一条轨道则实行标准停站方案。

图3 三股线路列车运行模式图

（4）单向双线路列车运行模式。如图4所示，单向双线路是采用快慢车方案最理想的条件，快车和慢车的运营完全独立，而且能够实现乘客在快慢车之间的同步换乘，但是伴随而来的高成本使得此种方案并不常见。

图4 单向双线路列车运行模式图

以图2所示的轨道设置形式为研究对象，对快慢车开行比例为1∶1时的停站方案进行研究，即开行1列慢车之后开行1列快车，2辆车组成1个发车对，相应的运行图如图5所示。

图5 快慢车运行示意图

其中h1表示慢车与下一列快车的发车间隔，h2表示快车与下一列慢车的发车间隔，h0=h1+ h2表示1个发车对的时间间隔。快车和慢车在区间的运行相互独立，只有在大站快车才能超越慢车行驶。为了保证列车之间的间隔，只有在快车发车后，慢车才能离开车站。

2 模型构建

2.1 目标函数构建

通过计算乘客的旅行时间和等待时间对乘客的满意度进行衡量，时间越短，满意度越高。 假设地铁线路一共有n个车站，将整条线路分割成n-1段，其中慢车在第i段的运行时间为快车在第i段的运行时间为慢车在第i站的停靠时间为快车在第i站的停靠时间为在h0时间内从i站到j站的乘客人数为qij，其中

图6中，“○”代表小站，“△”代表大站。将乘客分为以下3类进行讨论。

图6 乘客类型示意图

（1）乘客从一个大站旅行到另一个大站，只选择快车旅行。乘客在列车内的时间为列车运行时间与停靠在站台时间之和，即当xi=1且xj=1时 ，乘客的在列车内的总时间：

（2）乘客从小站旅行到其他车站。这里假设此类乘客只乘坐慢车旅行，即xi=0，乘客在列车内的总时间：

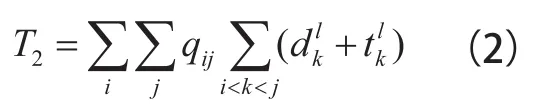
（3）乘客从大站出发到小站下车。此类乘客的选择有两种，一种是只乘坐慢车，另一种是先乘坐快车然后乘坐慢车。为了更详细地阐述，将此类问题分为3个子情况。

①如果出发站为大站，而目的站在出发站与下一个大站之间，那么乘客只能够选择乘坐慢车，此时乘客的在列车内的总时间：

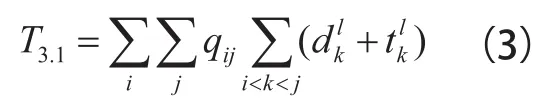
②如果下车站与出发站距离很远(中间间隔超过1个大站)，这时乘客会选择乘坐快车旅行，然后再换乘慢车到达终点，此时有：

其中，m=max{k|xk=1，k ∈[i，j]}。

③如果下车站与出发站之间恰好包含1个大站，此时乘客会估计自己的旅行时间，并选择更加快捷的方式。图7能够更好的阐述乘客的选择行为。

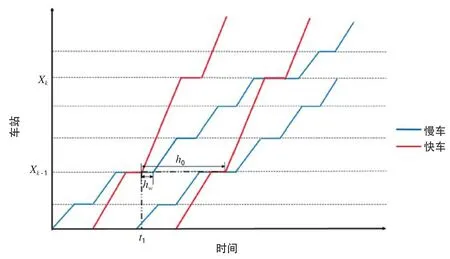
图7 乘客行为阐释图

为了保证快车和慢车不发生碰撞，两者的到站时间和出发时间间隔必须大于安全阈值hw。在时间区间[t1，t1+ hw]内到达的乘客更愿意选择慢车出行，然而在[t1+ hw，t1+ h0]内到达的乘客更愿意选择快车换乘出行，选择慢车出行的乘客占据了，而选择换乘的乘客占据了这样就得到了该情况中的旅行时间：

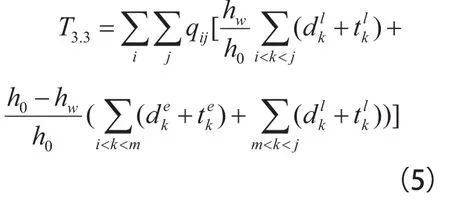
其中，m=max{k|xk=1，k ∈[i，j]}。

综上可以得到类型（3）的乘客在列车中的时间T3=T3.1+ T3.2+T3.3。

除此之外，乘客整个旅行时间还包括乘客等候列车的时间。类型（1）和类型（2）的乘客都需要等候的时间，而类型（3）的换乘乘客需要多出一次等候列车的时间，以此为依据可以将乘客分为两类，分别是不换乘乘客和换乘乘客。其中，不换乘乘客等候列车的时间：

换乘乘客等候列车的时间：

总等待列车时间：

乘客对于旅行时间和等待时间的主观感受并不相同，一般来说，乘客对等待时间的容忍度更低。为两个时间加上不同的惩罚因子c1、c2，其中等待时间的惩罚因子c1大于旅行时间的惩罚因子c2。综上所述，可以得到总的目标函数为：

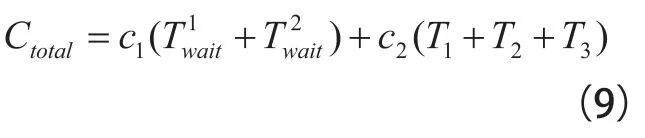
2.2 约束条件构建

根据快慢车的运行特点，可以从3个方面构建约束条件：列车运行时间约束、列车停靠时间约束和列车发车间隔约束。

由于地铁的硬件设施以及管理需求，列车的运行时间应该在一定的范围内。则有：

由于快车的速度比慢车的速度快，所以有：

本文考虑第二种轨道铺设方式，所以在大站，慢车需要停靠让快车通过，因此在大站慢车的停靠时间应该大于快车的停靠时间，即：

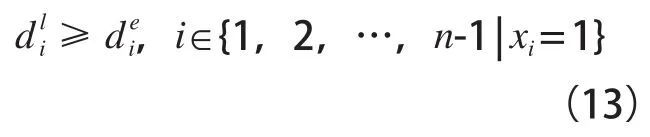
为了防止列车碰撞，要考虑列车的发车间隔约束，具体的参数设置如图8所示。

假设在大站j，快车到达与慢车到达的时间间隔为Tj1，在快车离开大站的时候，慢车还要停在该车站，其时间间隔为Tj2，慢车要在下一辆慢车到达之前离开，其时间间隔为Tj3。则有：

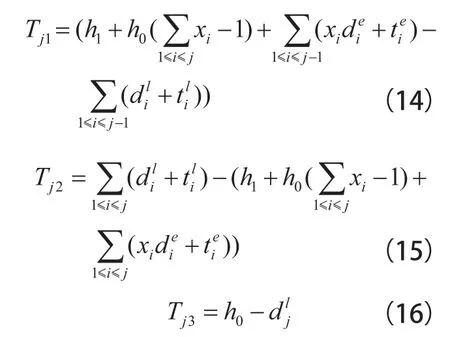
图8 发车间隔约束图

为了保证快车和慢车不发生碰撞，两者的到站时间和出发时间间隔必须大于安全阈值hw，则有：

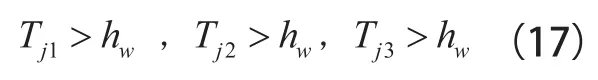
基于以上目标函数和限制条件，可以得到快慢车运行的规划模型：

可以看出模型的约束条件和目标函数都是线性的，也就是说，快慢车运行的模型是一个线性规划问题。

3 算例计算

假设某实行快慢车方案的地铁线路有11个车站，其中大站4个，分别是第1、4、8、11站。快慢车方案下的大站设置与发车间隔和车站的客流密度相关，为了使算例更加贴近实际，需要构造一个合理的客流密度以保证大站选择的正确性。假定从大站出发和驶向大站的乘客人数服从区间为[70，90]的均匀分布，而其他车站的乘客人数服从[50，70]的均匀分布，获得随机数qij。假设每个快慢车组的发车间隔为300 s，并按照经验数据拟定快慢车在区间运行时间以及列车停靠站台时间的区间范围。

根据以上条件，利用上文公式构建模型，求出列车的区间运行时间和停靠时间，从而得出合适的地铁运行图。在matlab中挂载IBM. ILOG.CPLEX.Optimizer.v12.5.1控件对上面的算例进行求解。

为了体现出乘客对列车旅行时间和等待列车时间容忍度不同对地铁运行图的影响，将算例分为两种情况进行讨论。

3.1 情况一

当c1/c2=1时，也就是以乘客所有旅行时间之和为目标函数，通过计算得到h1=160，h2=140，c=3 088 709，即第一辆慢车运行160 s后第一辆快车发出车，第一辆快车发出后140 s第二辆慢车发车。根据模型计算可以得到列车的区间运行时间，继而得到地铁运行图，如图9所示。

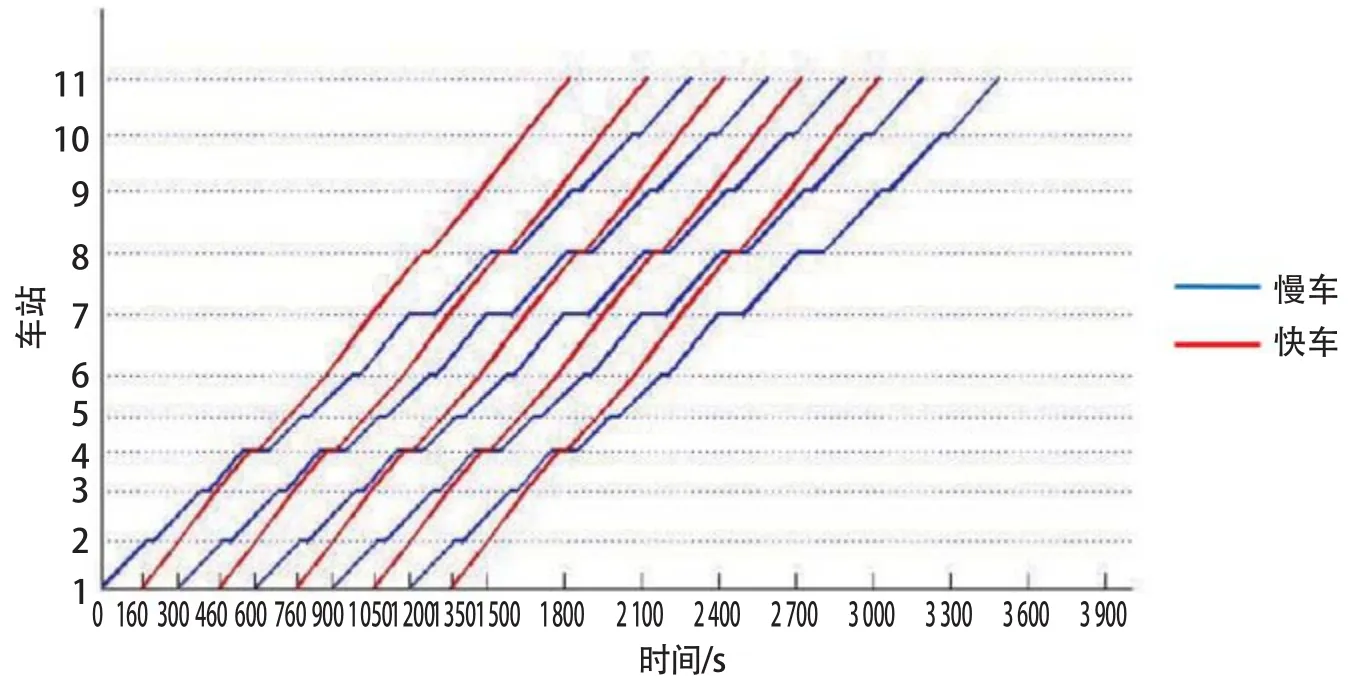
图9 情况一快慢车运行图

为了与普通地铁运行方式进行对比，也计算了普通方式下地铁的运行方案，假定列车发车间隔为150 s，在同样的客流密度下，得到c=3 283 170，其运行图如图10所示。

从旅客的总体等待时间来看，普通的地铁运行方式的确比快慢车停站方式下的等待时间更长，即快慢车停站方式能够提高乘客的满意度。

图10 情况一普通地铁运行图

3.2 情况二

假设c1/c2=2，也就是说，乘客对旅行时间的容忍度是等待时间的2倍。得到h1=160，h2=140，c=3 577 052，再根据模型计算出列车的区间运行时间和停靠时间，得到地铁运行图如图11所示。

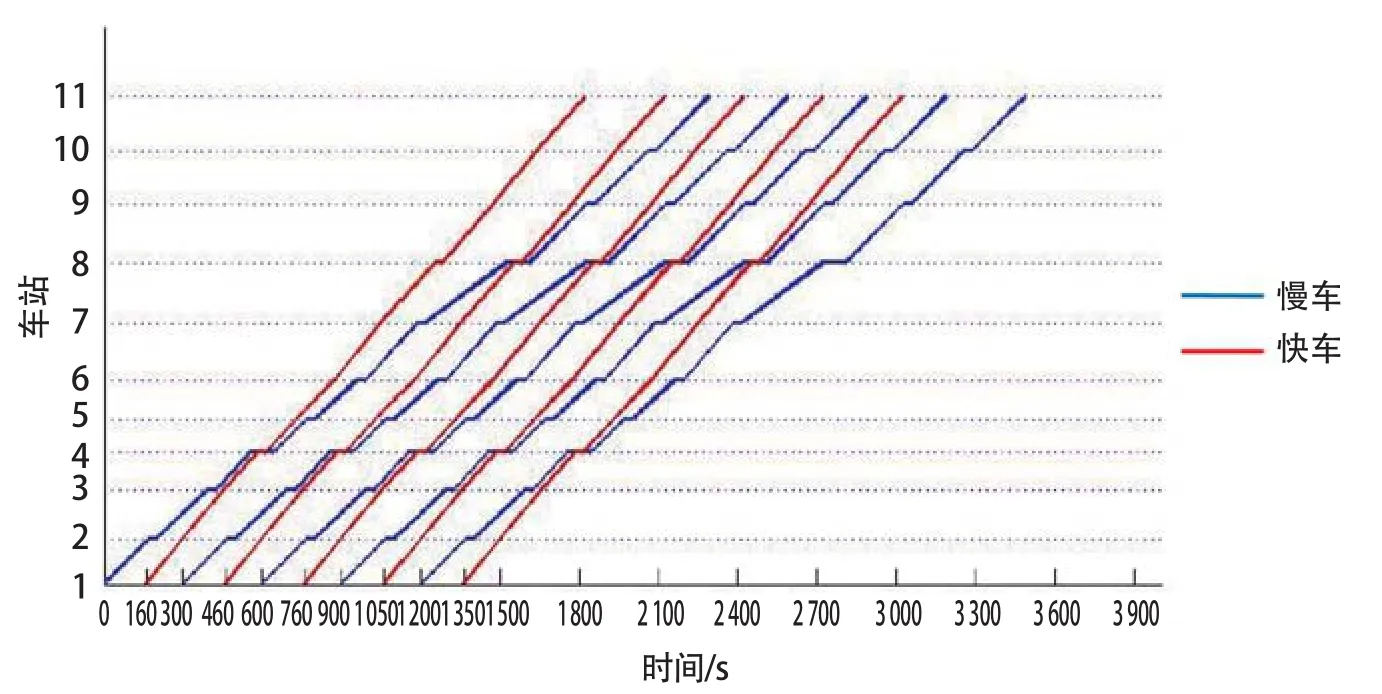
图11 情况二快慢车运行图

可以看到，c1/c2的变化会对列车区间运行时间和列车停靠时间产生明显的影响。与情况一类似，考虑不同乘客偏好下的普通运行方式的列车方案变化。经过计算得到采用普通运行方式时c=4 094 070，其运行图如图12所示。

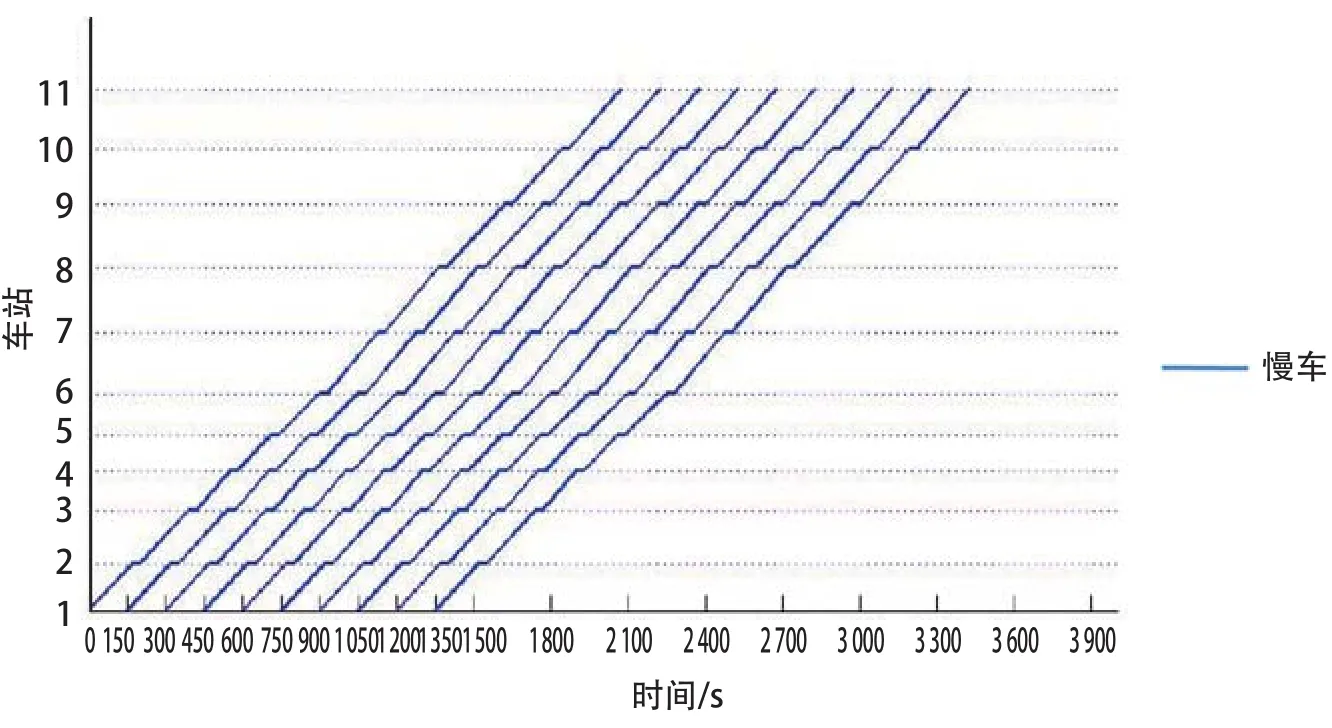
图12 情况二普通地铁运行图

3.3 数据分析

对算例的计算结果进行分析，可以得出以下结论。

（1）对比图9和图11中7、8站间列车运行情况，发现当乘客对等待时间的容忍度更低的时候，也就是c1/c2=2时，列车在该区间运行时间延长，速度减缓。这就意味着如果考虑到乘客对旅行时间和等待时间的不同的容忍度，列车的停站方案会有很大的不同。

（2）当c1/c2=1时，快慢车运行方式的目标函数值为3 088 709，相比普通运行方式的目标函数值3 577 052更低，也就是说在快慢车运行方式下乘客的满意度更高。同样的，当C1/ C2=2时，采用快慢车运行方式得到目标函数值为3 577 052也要小于普通方式的目标函数值4 094 070，由上述比较可以发现无论乘客对旅行时间和等待时间容忍度的比例有何变化，采用快慢车停站方案的目标函数值均要比普通列车方案小，也就是说，采用快慢车的停站方案能够提高乘客的满意度。

4 建议

经过算例的检验，证实本文模型可以有效解决快慢车停站方案的规划问题，但是模型还存在一些不足之处。

（1）为了便于建模和求解，本文对停站方案问题做了很多简化，如仅考虑了单线单向运营的情况，没有考虑城市轨道交通线路成网运营、线路间换乘以及共线运营等情况对单线停站方案制定的影响等。由于国内城市轨道交通线路的布局、运营特点不同，今后可以对这些复杂背景下的方案制定问题展开深入研究。

（2）仅对静态均衡客流的情况进行了研究，这种情况下的总交通需求是稳定不变的。而实际客运网络中的交通需求具有动态性和不确定性，以后可以考虑使用鲁棒优化，选择更为合理的函数分布以应对客流变化造成的影响。

5 结论

本文在前人研究的基础上，对影响快慢车运行时间的因素进行分析，构建出以最大化乘客满意度为目标的模型，经过算例的验证得出较为合理的快慢车运行方案。

通过以上的阐述和计算，证实采用快慢车运行的方案可以有效减小乘客的旅行总时长，并能够提高乘客的满意度。当考虑不同乘客对等待时间和在列车中旅行时间的容忍程度时，快慢车运行图会有明显的改变。

[1] Fischetti M, Salvagnin D, Zanette A. Fast approaches to improve the robustness of a railway timetable [J]. Transportation Science，2009，43 (3)：321-335.

[2] Freyss M，Giesen R，Mu☒oz J C. Continuous approximation for skip-stop operation in rail transit [J]. Transportation Research Part C：Emerging Technologies，2013 (36)：419-433.

[3] Kroon L，Maróti G，Helmrich M R, et al. Stochastic improvement of cyclic railway timetables[J]. Transportation Research Part B：Methodological，2008，42 (6)：553-570.

[4] Vansteenwegen P，Van Oudheusden D. Decreasing the passenger waiting time for an intercity rail network [J]. Transportation Research Part B：Methodological，2007，41 (4)：478-492.

[5] Vuchic V R. Urban Transit[M]. Wiley：2005.

[6] 陈军华，张星臣，徐彬，等. 高速铁路列车运行图稳定性及其影响因素分析[J]. 物流技术，2011，30 (8)：81-84.

[7] 郭钰. 城市轨道交通列车停站方案优化研究[D]. 北京：北京交通大学交通运输学院，2009.

[8] 屈明月，黄树明. 城市轨道交通快慢车方案研究[J]. 铁道运输与经济，2012 (4)：79-82.

[9] 周方明，程先东，谢美全，等.地铁列车初始布点的鲁棒性研究[J]. 物流技术，2010，29(15)：47-51.

[10] 王琳. 城市轨道交通快慢车运营组织研究[D]. 北京：北京交通大学，2013.

责任编辑 凌晨

A Model of Customer Satisfaction-based for Express/Local Train Operation

Tang Runyu, Gao Yuan

With the growing awareness of the traffi c demand, optimized planning of urban rail transit has become an important way to solve the problem of traffi c congestion. The paper focuses on a special metro stop plan called express/local, which is the only way to provide regular service among all stations as well as higher-speed service stopping only at major stations. To maximize passenger satisfaction, which is to minimize the total travel time for passengers, we construct a linear programming model and use Cplex programming to work out the model. After comparing the passenger travelling time between express/ local mode and standard mode, a conclusion is worked out and the express/local operation could provide the service of better passenger satisfaction.

metro, express/local operation, passenger satisfaction, train running time schedule

U292.4

2015-03-31

唐润宇：轨道交通控制与安全国家重点实验室, 北京交通大学, 研究生，北京 100044