重型钢轨质量调谐系统振动特性研究

常 健 耿传智

重型钢轨质量调谐系统振动特性研究

常 健 耿传智

为了探明新型重型钢轨质量调谐系统（HTMD）的振动特性，为既有轨道减振改造提供参考，利用ANSYS软件建立HTMD轨道三维有限元模型，分析HTMD轨道的振动响应和减振特性。研究结果表明，HTMD轨道的低阶模态分布比较密集，随着扣件刚度增大，轨道结构固有频率增大；当扣件刚度为6 kN/mm时，HTMD轨道固有频率为18.821 Hz；HTMD轨道在10～100 Hz频段，钢轨垂向加速度Z振级有20 dB左右的减小，比普通轨道有很大程度的降低，道床振动有15 dB左右的降低，与普通浮置板轨道结构相当。

HTMD轨道；质量调谐系统；振动响应；减振特性；研究

1 HTMD轨道结构设计

H T M D轨道是在2根钢轨中间及两侧悬放安置重型混凝土块，钢轨与混凝土块之间用粘弹性材料粘结，从而构成1个典型的质量-弹簧隔振系统（图1）。该质量块与钢轨一起参与振动，较大地提高了系统的参振质量，从而有效地降低系统的振幅及固有频率，实现减振的目的。同时，H T M D轨道通过自身的振动，消耗一部分的振动能量，成为一种耗能机构，对振动的控制有一定的积极作用。

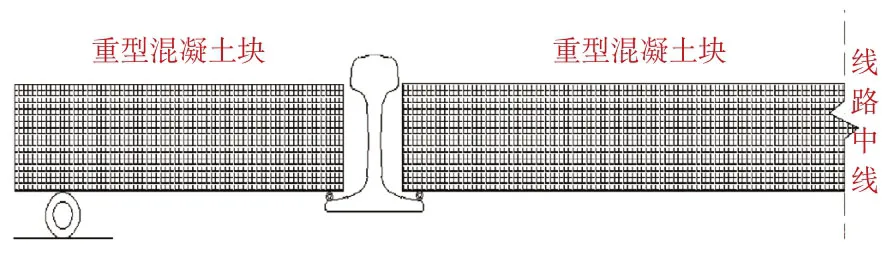
图1 HTMD轨道结构示意图

2 结构有限元模型及参数

本论文对HTMD轨道从结构有限的空间出发，针对既有轨道结构进行质量调谐系统的设计，建立有限元三维模型（图2），选择合理的模型参数，分析HTMD轨道对钢轨及道床固有频率、动力响应和减振性能的影响。

图2 HTMD轨道有限元模型

（1）钢轨采用标准6 0轨，质量m=60.64 k g/m，截面面积A=77.45 cm2，弹性模量E=210 GPa，泊松比μ=0.3，有限元模型中采用Solid45单元模拟钢轨实体，计算长度25 m。

（2）扣件刚度取k=6、25、50 kN/mm，阻尼7.5×104N·s/m，运用Combin14单元模拟。

（3）质量系统采用壳结构，板连续设置，2轨中间板宽1.35 m，钢轨两端质量板各宽0.5 m，板厚120 mm，采用Shell63单元进行模拟。

（4）质量单元和钢轨的连接运用弹簧模拟，弹簧单元使用Combin14单元，该处橡胶要求硬度较大，以保证质量单元的稳固连接，故刚度设置为k=2×108kN/mm。

3 固有频率分析

HTMD轨道作为一种新型的减振轨道结构，要了解其动力性能，需对其有限元三维模型做结构模态分析。结构模态是振动系统特性的一种表征，输出参数有系统结构的各阶固有频率以及对应的振型。本文在固有频率分析中扣件刚度分采用k=6、25、50 kN/mm，计算分析普通轨道和HTMD轨道等2种轨道结构的固有频率变化。表1给出了2种轨道结构前6阶垂向振动固有频率计算结果，由表1计算结果可知：

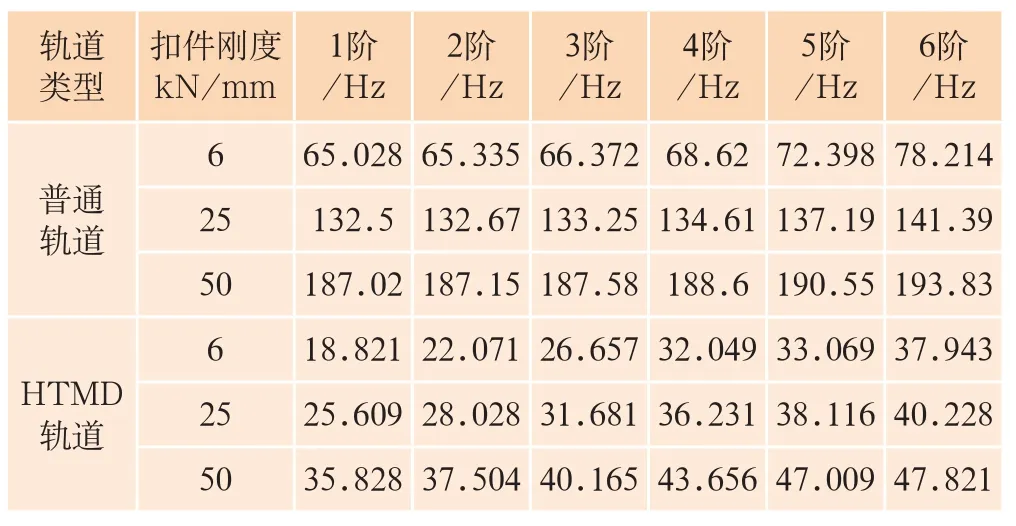
表1 2种轨道结构固有频率

（1）采用刚度相同的扣件时，H T M D轨道结构固有频率较普通轨道结构固有频率有大幅下降，当扣件刚度为k=25 k N/m m时，HTMD轨道结构的1阶固有频率为25.609 Hz，是普通轨道的1/5；

（2）扣件刚度越大，轨道结构固有频率越大。同一种轨道结构，扣件刚度为k=50 kN/mm时的1阶级固有频率约为扣件刚度为k=6 kN/mm时的2倍；

（3）随着扣件刚度增大，普通轨道固有频率增幅较HTMD轨道固有频率增幅更大。

4 HTMD轨道减振特性

为了得到H T M D轨道结构的减振特性，需要将列车测试荷载P(t)施加在HTMD轨道结构的有限元三维模型上（图3、4），用来计算分析轨道及道床的振动响应，并与普通轨道结构进行对比分析研究。计算结果分析如下：

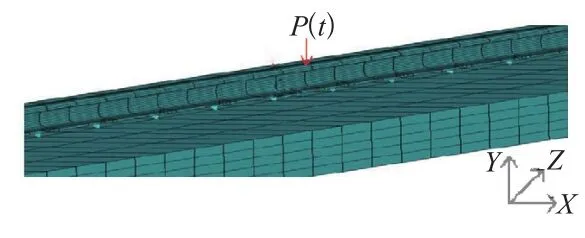
图3 载荷施加三维有限元模型图

图4 测试载荷施加模型

（1）图5给出了扣件刚度k=25 kN/mm时普通轨道和HTMD轨道的钢轨位移时程曲线，由图5位移时程曲线可知，扣件刚度采用k=25 kN/mm时，普通轨道钢轨的最大位移值为1.6 mm，HTMD轨道钢轨的最大位移为0.9 mm，可见，HTMD轨道结构钢轨位移较普通轨道减幅约44%；

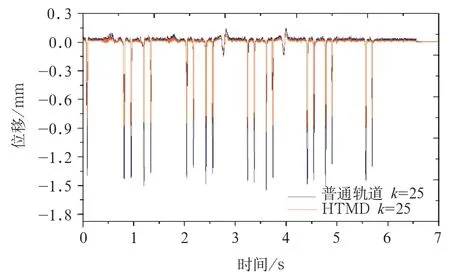
图5 普通轨道和HTMD轨道钢轨位移时程曲线

（2）图6给出了H T M D轨道不同扣件刚度的钢轨位移时程曲线，由图6位移时程曲线可知，HTMD轨道扣件刚度分别为k=6、25、50 kN/mm时，钢轨最大位移值分别为2、0.9、0.6 m m，说明随着扣件刚度的增大，HTMD轨道中钢轨位移显著减小，这对列车运行的安全性和稳定性越有益；

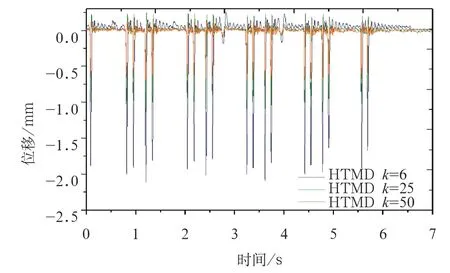
图6 HTMD轨道不同扣件刚度钢轨位移时程曲线

（3）图7和图9给出了扣减刚度为k=25 kN/ mm时普通轨道和HTMD轨道的钢轨加速度频谱，由图7和图9钢轨加速度频谱可知，采用相同刚度扣件时，HTMD轨道对150 Hz以上高频段振动频率成分有很高的衰减率，而普通轨道对0～500 Hz频段基本无衰减；

（4）图8、9、10给出了HTMD轨道结构扣件刚度为k=6、25、50 kN/mm时的钢轨加速度频谱，由图8、9、10钢轨加速度频谱可知，3种不同刚度扣件的HTMD轨道对150 Hz以上高频段振动都有很好的衰减作用。但，随着扣件刚度增大，HTMD轨道对低于150 Hz的频段并未见明显衰减，说明HTMD轨道钢轨加速度在低于150 Hz频段对扣件刚度变化表现不敏感。

图7 普通轨道钢轨垂向加速度频谱

图8 HTMD轨道钢轨垂向加速度频谱

图9 HTMD轨道钢轨垂向加速度频谱

图10 HTMD轨道钢轨垂向加速度频谱

（5）图11～14给出了普通轨道和HTMD轨道时不同扣件刚度情况下，钢轨、道床1/3倍频程计权Z振级。由图11可看出，当扣件刚度k=25 kN/mm时，HTMD轨道钢轨Z振级较普通轨道有20 dB的降低；由图12可以看出，随着扣件刚度的降低，HTMD轨道钢轨的振级未见明显降低，说明HTMD轨道对扣件刚度表现不敏感；由图13可以看出，HTMD轨道道床Z振级较普通轨道有15 dB的降低；由图14可以看出，随着扣件刚度的降低，HTMD轨道对10～100 Hz频段的道床Z振级有一定的降低，0～10 Hz及100～200 Hz频段道床Z振级基本没有减小；

图11 普通轨道与HTMD轨道钢轨1/3倍频程计权Z振级

图12 HTMD轨道不同扣件刚度时钢轨1/3倍频程计权Z振级

（6）表2给出了普通轨道和HTMD轨道在不同扣件刚度情况下，钢轨、道床1/3倍频程Z振级汇总。综合图11～14及表2对比分析可知，扣件刚度降低，钢轨Z振级增大，道床Z振级减小。普通轨道钢轨Z振级在95.51～104.40 dB，HTMD轨道钢轨Z振级在77.35～84.01 dB；普通轨道道床Z振级在63.05～60.62 dB，HTMD轨道道床Z振级在51.42～46.79 dB。可见，HTMD轨道较普通轨道钢轨Z振级有20 dB左右的降低，道床有15 dB左右的降低，说明HTMD轨道减振效果显著。

5 结论

本文通过建立轨道模态分析有限元分析模型，分析了HTMD轨道的振动特性，并与普通轨道振动特性进行对比，证明了HTMD轨道对中高频率振动的衰减效果，结论如下：

图13 普通轨道与HTMD轨道道床1/3倍频程计权Z振级

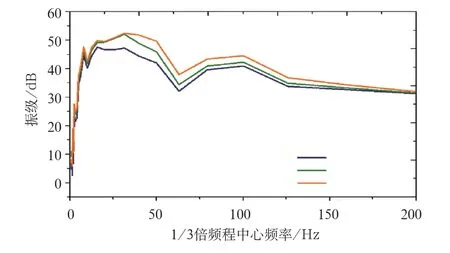
图14 HTMD轨道不同扣件刚度道床1/3倍频程计权Z振级

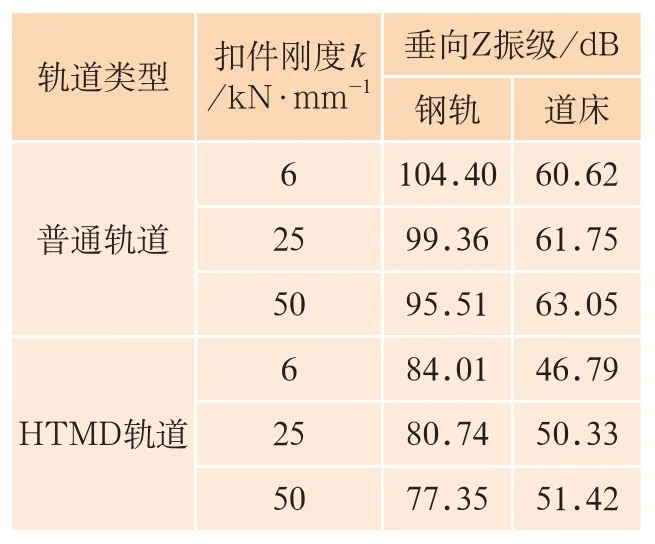
表2 不同轨道不同扣件刚度时钢轨、道床垂向Z振级

（1）H T M D轨道在使用一般弹性扣件时，其1阶固有频率在20～30 Hz，前6阶固有频率亦均低于40 Hz，较普通轨道有很大程度的降低；

（2）HTMD轨道的固有频率受到扣件的刚度的影响，扣件刚度增大轨道振动频率随之增大，因此，HTMD轨道和弹性扣件进行刚度优化匹配可达到更好的减振效果。当HTMD轨道和高弹性扣件进行匹配使用时，其1阶固有频率降至20 Hz以下，接近或等同于浮置板轨道，对地铁振动能起到很大程度的降低，是一种高效的可用于既有运营线路改造的减振措施；

（3）HTMD轨道较普通轨道，钢轨有20 dB左右的减振效果，道床有15 dB左右的减振效果，与普通浮置板轨道结构相当，且其施工便利、经济实用，更方便运用于既有线改造，为一种理想的减振轨道结构。

（4）钢轨高频振动易使钢轨产生波磨，HTMD轨道结构对高频振动良好的减振作用，会减少钢轨波磨的发生。

[1] 余庆. 地铁运营对环境影响分析及减振技术研究[D]. 上海：同济大学，2011.

[2] 翟婉明. 车辆-轨道耦合动力学[M]. 第3版. 北京：中国科学出版社，2007.

[3] 辜小安，刘宪章，张春华. 地铁环境振动预测方法浅析[M]. 环境工程，1996，14(5).

[4] 李守承. 地铁引起环境振动及房屋浮置楼板隔振研究[D]. 上海：同济大学，2008.

[5] GB50157-2003地铁设计规范[S]. 2003.

责任编辑 朱开明

Study on Vibration Characteristics of Heavy Rail Quality Tuning System

Chang Jian, Geng Chuanzhi

In order to fi nd out the vibration characteristics of the new type heavy rail quality tuning system (HTMD), and a reference to be provided for the reconstruction to have vibration control on the existing tracks, by using the ANSYS software to establish the three-dimensional fi nite element model of the HTMD track, the paper makes an analysis on the vibration response and vibration control characteristics. The results show that the HTMD track has low order modal layout density. With the increase of fastener stiffness, track structure natural frequency is higher. When the fastener stiffness is 6 kN/mm, the HTMD track natural frequency is 18.821 Hz. When the HTMD track in the frequency band of 10 ～100Hz, the rail vertical acceleration Z vibration level is reduced to around 20 DB, much lower than ordinary rail natural frequency, ballast bed vibration have reduced by 15dB, and the vibration of ordinary fl oating slab track structure is equivalent to it.

HTMD track, quality tuning system, vibration response, vibration response, study

U213.2

2015-07-30

常健：同济大学铁道与城市轨道交通研究院，硕士研究生，上海 201804