地采诱发建筑物损害识别的进化支持向量机模型
2015-12-21蒋成荣彭平安王李管
蒋成荣,彭平安,王李管
地采诱发建筑物损害识别的进化支持向量机模型
蒋成荣1,彭平安2,王李管2
(1. 攀枝花学院资源与环境工程学院,四川攀枝花,617000;2. 中南大学资源与安全工程学院,湖南长沙,410083)
针对采动区建筑物损害程度的影响因素较多且各因素呈现非线性、多重共线性等特点,应用支持向量机理论并结合工程实际,提出基于支持向量机理论的地采诱发建筑物损害效应预测方法。综合考虑地质采矿方面和建筑物本身因素,选取10个影响砖混结构建筑物采动损害程度的因素作为模型的输入,将砖混结构建筑物的损害等级及建筑物的最大裂缝宽作为模型的输出,以32个建筑物采动损害的工程实例作为学习样本进行训练;采用RBF核函数,建立建筑物损害等级预测的支持向量机分类和最大裂缝宽回归模型;为提高预测模型的泛化能力和预测精度,应用遗传算法选择支持向量机的模型参数,并对6组待判样本进行判别。研究结果表明:建立的遗传算法优化支持向量机分类与回归模型对地采诱发建筑物损害效应预测效果良好,评估结果与实际结果相吻合。
地下开挖;建筑物损害;损伤评价;支持向量机;遗传算法;预测
地下工程(隧道、基坑)开挖和矿山采掘不可避免地会对周围岩土体产生扰动,进而对邻近的建筑物产生影响,严重时会危及建筑物的安全。随着经济的发展和城镇化水平的提高,地表建筑物越来越密集,建筑物价值也越来越高,地下工程开挖与地表建筑物安全之间的矛盾日益突出,这对建筑物损伤风险的定量化要求越来越高[1−5],为此,研究地下开挖区临近建筑物的风险评估并针对损害建筑物提出相应的防御措施,对于保证建筑物的安全和正常使用具有重要意义。近年来,人们对地采诱发建筑物损害的机制、预测与处治尤其是开挖引起的建筑物破坏风险评估进行了大量研究[4−9],如边亦海等[4]采用建筑物的裂缝宽度评价深基坑开挖引起的建筑物潜在破坏。Burland等[6]在评估伦敦地下隧道开挖引起的建筑物破坏时,将建筑物假设为简支梁,通过计算最大拉应变来确定潜在的破坏种类和风险级别;Finno等[7]提出了分层梁模型,通过计算最大弯曲应变和剪切应变,来判断是否产生裂缝并评定破坏风险等级;Soon等[8]提出了四阶段方法来评估开挖造成的建造物破坏程度,该方法通过计算角变位和水平应变来确定结构的破坏风险等级。此外,国内外相继出台了一系列法律法规,如英国颁布了建筑物损害等级规范[1],我国国家煤炭工业局也制定了“建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程”[10],给出了矿山开采塌陷引起的建筑物损坏判定等级,但在理论、方法体系上的论述仍然不够,也缺少工程实践的范例。而影响地采诱发建筑物损害风险评估的因素具有复杂性、多样性和非线性的特点,很难提出准确、通用的判别准则。近年来,一些研究者提出模糊综合评价法[11]、神经网络[12]和可拓分析法等软科学方法对其进行评估,如Lian等[11]提出了煤矿开采砖混结构破坏等级评价的模糊数学方法;郭文兵等[12]采用基于模糊等价关系的模糊聚类分析方法和自适应BP神经网络技术建立建筑物采动损坏程度的预测模型,对采动影响下建筑物损害程度进行了分类研究。刘立民等[13]基于可拓学的理论和方法,建立了建筑物损坏等级识别和评判的可拓学分析方法的数学模型。上述系列方法和模型具有一定的优点,但也存在一些不足,如Burland 等[6]提出的方法均以应变或角变位为研究对象,采用的破坏指标不直观,理解起来比较困难,物理意义也不是很明确。模糊综合评判法[11]常对各指标确定隶属度并赋予不同权重,会带有一定的主观性和随意性;BP神经网络方法[12]存在收敛速度慢、易陷入局部最优及隐含层确定具有主观性等弱点;可拓变换[13]难以确定合适的关联函数等:因此,要准确评价地下开挖工程对临近建筑物损害影响的程度,上述分类方法还不能很好地服务于工程实践,还需要探索更科学有效的评价方法。支持向量机(support vector machine,简称SVM)[14]具有较强的非线性动态处理能力,无需知道数据的分布形式和变量之间的关系,可实现高度非线性映射,对于处理小样本、非线性等实际问题,支持向量机具有突出的优点,与神经网络相比,具有泛化能力强、容易训练、没有局部极小值、推广能力和非线性处理能力较强等优点,但对影响其性能的SVM参数及其核函数参数的选取问题还没有完善的准则可以参考;遗传算法(GA)[15]借鉴了生物进化规律,对于寻优问题有很好的自适应优化搜索能力。本文作者SVM和GA相结合,以寻找SVM的全局最优参数,从而较准确地对地采诱发建筑物损害予以合理评估。
1 SVM分类和回归计算原理
1.1 SVM分类
考虑1个模式分类器,设待训练样本集为={(1,1),(2,2),…,(x,y)}。其中,x为输入空间参数,y为分类标识参数,x∈R,y∈{−1,+1},=1,2,…,。若存在∈R,∈R,使得对于任意的(x, y)有y(•x+)≥1(为分类超平面的法向量,为偏移量),则称训练集线性可分。若这个向量集合没有被超平面错误地分开,并且离超平面最近的向量与超平面之间的距离是最大的,则这个向量集合被这个最大间隔超平面(最优超平面)分开,见图1。
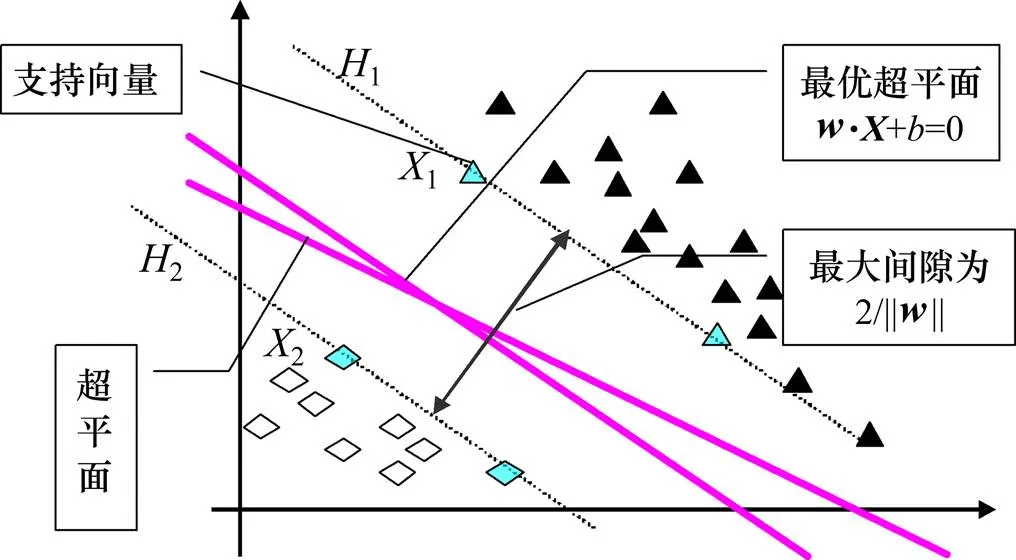
图1 SVM原理图
SVM算法核心是找出支持向量及其系数构造最优分类面[13−14, 16]。而此最优分类面的构造问题实质上是在约束条件下求解1个二次优化问题,以得到1个最优的决策函数,其最优分类超平面为
为了在数据线性不完全可分情况下构造最优分类超平面,引入松弛变量≥0,同时引入惩罚参数,用来平衡和。是可调参数,表示对误判样本的惩罚程度,越大,表示对误判样本的惩罚程度越大,由此构造软间隔最优分类超平面:
引入Lagrange优化方法,根据Wofle的对偶理论可以将上述分类问题转化为它的对偶问题求解,即
而对于线性不可分问题,SVM通过引入核函数将内积运算转化为在输入空间的计算,即。则SVM的求解对偶最优化问题可转换为
1.2 SVM回归
引入松弛变量,并使用Lagrange 乘子法,得到优化问题的对偶式:


非线性回归问题的实施步骤如下。

第3步:计算
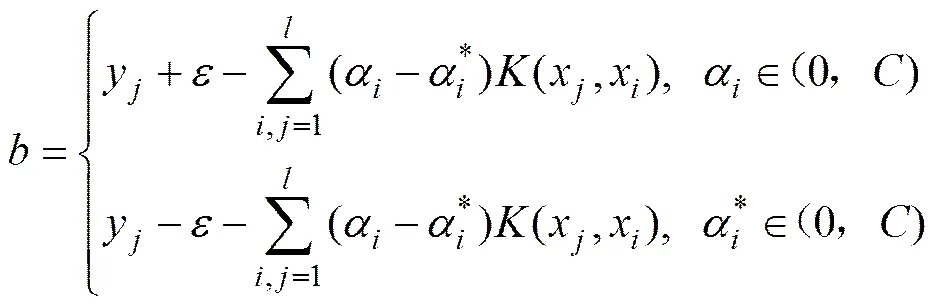
第4步:构造非线性函数
2 基于GA的SVM参数优化
在SVM算法中,与核函数参数的选择对其算法的推广预测能力和效率影响很大。通常采用人工试算的方法,传统的参数选取方法是以经验为指导,人为挑选出较满意的解。这种方法主观性太强,效率较低,针对处理不同程度的复杂问题很难实现参数的正确选取和最优搭配,这在很大程度上制约了SVM的进一步发展。遗传算法(GA)是基于生物进化过程中优胜劣汰规则与群体内部染色体信息交换机制的一种处理复杂优化问题通用性很强的方法,它具有通用性强、可脱离局部最优、寻优效率较高和搜索速度快等优点[15−17],将SVM与GA相结合,可实现各种优化的目标。为此,本文提出基于遗传算法的SVM分类与回归方法,采用GA来搜索最佳的SVM参数。其具体实现过程如下。
Step 1编码。将解空间的数据误差惩罚系数和核函数参数表示成遗传空间的基因型数据,这些基因型数据的不同组合就构成了不同的点。本文采用二进制编码法。
Step 2初始化种群。随机产生个初始基因型数据,每个基因型数据称为1个个体,个个体构成1个群体。GA以这个字符串为初始点开始迭代。
Step 3个体适应度计算。计算个体适应度,并判断是否符合优化准则。若符合,则输出最佳个体及其代表的最优解,并结束计算,否则转向Step 4。
Step 4选择。根据每个个体的适应度选择一些优良的个体遗传到下一代群体中。适应性强的个体被选中的概率高,适应度低的个体可能被淘汰。
Step 5交叉。将群体内的各个个体随机搭配成对,对每个个体以某个概率(称为交叉概率)交换它们之间的部分染色体。
Step 6变异。对群体中的每个个体以变异概率改变某个或某些基因座上的基因为其他的等位基因。
Step 7判断运算。判断新一代群体是否满足结束条件,若满足,则停止;若不满足,则转至Step 3步骤继续进行计算。
Step 8应用。用训练好的GA-SVM解决实际问题。其计算流程图见图2。

图2 地采诱发建筑物损害风险的GA-SVM评价流程
3 地采诱发建筑物损害效应预测的SVM模型及其应用
3.1 模型输入输出参量的确定
建筑物损伤效应受多种控制因素的影响,参考有关研究及工程实践[1−12],还需考虑分析资料的易获性和代表性。综合考虑地质采矿方面和建筑物本身方面因素,选取建筑物状况特征值、建筑物与空区位置关系特征值、建筑物长度、建筑物宽度、采动程度综合系数、采深、采厚、覆岩平均普氏系数、倾角和顶板管理方法特征值共10个因素作为模型的输入参量。其中:建筑物状况是建筑物的修建年限、地基、基础性质、建筑材料和结构以及建筑物质量等方面的综合反映,分级是用定性语言描述的,在计算中按表1中量化值计算;建筑物与采空区的位置关系可根据建筑物移动盆地内位置的不同及受到开采影响破坏程度划分为5种情况,如表2所示;顶板管理方法特征值为0或1,当未采用有效顶板管理方法时取0,反之取1。

表1 建筑物状况特征值

表2 建筑物在移动盆地中的位置
在确定建筑物损伤时,参考BRE建筑物破坏分类表[18]、Rankin评估系统[19]、英国建筑物损害等级规 范[20]、波兰建筑物损害规范[20]和“建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程”[10],将建筑物损害等级分为Ⅰ(忽视)、Ⅱ(轻微)、Ⅲ(中等)和Ⅳ(严重)共4个类别,给出建筑物的最大裂缝宽度,并将建筑物损坏类别和其最大裂缝宽度作为模型的输出。
3.2仿真数据采集及数据归一化处理
为了验证本文提出的地采诱发建筑物损害效应预测的遗传算法优化SVM模型的有效性和实用性,以郭文兵等[12]搜集的30组建筑物采动损坏实例作为SVM模型的学习训练样本(表 3)和测试样本(表 4),其数据集可视化图见图 3。
为将具有不同量纲和取值范围的数据通过一定的处理,使其变换到相同的取值范围内,即具有相同的尺度,需对样本数据进行归一化处理。为此,对SVM预测模型的输入变量采用如下规范化方法进行预处理:设变量最大值为max,最小值为min,某一个样本的规范化变量norm定义为

表3 建筑物采动损害典型实例训练集

表4 建筑物采动损害典型实例测试集
于是,每个输入变量的取值范围都在[0, 1]之间。
3.3 参数寻优
结合文献[17−18]中研究成果,选取RBF核函数。对于GA-SVM 模型,只需通过GA找到适合样本特性的RBF核参数和惩罚因子,来消除因SVM 参数设置不当导致的预测准确率低的风险。利用GA寻找SVM 中最佳的尺度参数和惩罚因子,关键是染色体编码上:首先定义染色体中基因个数为20,并按经验设定和的范围;然后,按设定的范围进行离散化及二进制编码,如果∈(0,10),步长为10/1 024,其二进制编码为0000000001~ 1111111111,那么,二进制的每 1 位可作为 1 个基因,得到的二进制串为=12…10;∈(0,100),其步长为100/1 024,二进制串为0000000001~ 1111111111,得到=l2…l0,则有=12…10l2…l0,其映射函数可记为
当结束遗传操作后还需要进行解码,将染色体转换成实际的尺度参数和惩罚因子即可。
3.4 建筑物损伤等级评估
以文献[12−13]提供的30组实测资料为基础建立建筑物采动损坏评估的SVM模型,数据集见表3。评价建筑物最大裂缝宽度时,SVM模型输入向量为(,,,,,,,,,),模型输出损害等级,建立映射(,,,,,,,,,)。而对于分类问题,影响SVM分类效果的参数主要有2个:误差惩罚参数和核函数参数。误差惩罚参数的作用是在确定的数据子空间中调节学习机器置信范围和经验风险的比例使学习机器的推广能力最强,不同数据子空间中最优的不同。核函数参数主要影响样本数据在高维特征空间中分布的复杂程度。采用Matlab 编写GA 优化SVM 模型参数程序,结合Libsvm 支持向量机工具箱,采用训练样本交叉验证的方式确定支持向量机参数和,调用Matlab遗传算法工具箱,实现逐步启发式优化。经反复试验,设置设定和的取值范围为:∈(0, 100),∈(0, 100);最大进化代数为100次,最大种群数量为20个,交叉和变异概率分别为 0.90和 0.05,并设置支持向量机进行5折交叉验证,通过计算可得适应度与进化代数的关系曲线,见图4。最终确定最优参数为16.881,为90.305,此时训练精度为93.33%。由图4 可知:最佳适应度随着进化代数的增加而增大,这正是GA进化的效果;在进化23 代后,最佳适应度收敛,通过计算,可得到最佳参数对 (,) =(12.606 3, 0.622 56),即GA-SVM 模型对学习样本的判别结果全部准确(表3),由此可认为分类模型已很稳定。根据学习好的建筑物损伤识别的GA-SVM 模型对6 个待判样本进行判别,判别结果与实际结果完全相符,并与BP神经网络方法[4]预测结果一致,误判率为0,见表4。由此可见:GA-SVM 模型用于地采诱发建筑物损害识别预测是可靠和有效的。

图4 损伤等级GA参数选择适应度曲线
3.5 建筑物最大裂缝宽度预测
预测建筑物最大裂缝宽度时,SVM模型输入向量为(,,,,,,,,,),模型输出损害等级,建立映射(,,,,,,,,,)。在SVM回归问题中,惩罚因子决定函数的拟合优度,过高会得到更多的支持向量,但会影响SVM的回归性能,为此选择1个合适的惩罚因子用于回归预测分析尤为重要。采用不敏感参数解释回归曲线的精确度,越大,则回归曲线的泛化性能会越低。样本训练取核函数为高斯核函数(RBF),利用上述遗传算法的步骤对SVM的参数和的最佳组合进行优化,同样采用二进制编码方法,获得最佳参数(,)。其GA各控制参数设置如下:群体规模为20,最大进化代数为 100,的编码长度为 5,的编码长度为 5,杂交率为 0.9,变异率为 0.05。各参数的优化区间设为:0≤≤100,0≤≤100。并用平方相关系数(squared correlation coefficient,2)和均方误差(mean square error,MS)作为最终评价指标:
其中:T为训练集数据;O为预测数据;为个数。
通过计算可得最大裂缝宽度GA参数选择适应度与进化代数的关系曲线,见图5。当模型最佳参数=5.246 5,=0.214 96时,测试样本MS为0.001 486,2为0.960 53,见图6。从图6可看出:用SVM回归机通过训练样本得出的预测曲线拟合程度良好。
BP 神经网络和 GA-SVM 预测模型的预测误差分析比较结果见图 7。根据文献[13],最大裂缝宽度最大绝对误差为1.98 mm,相对误差较大。本文GASVM模型最大绝对误差仅为0.86 mm,远低于 1.98 mm,可见本文新提出的 GA-SVM 预测模型的预测精度高于传统的BP神经网络模型的预测精度。
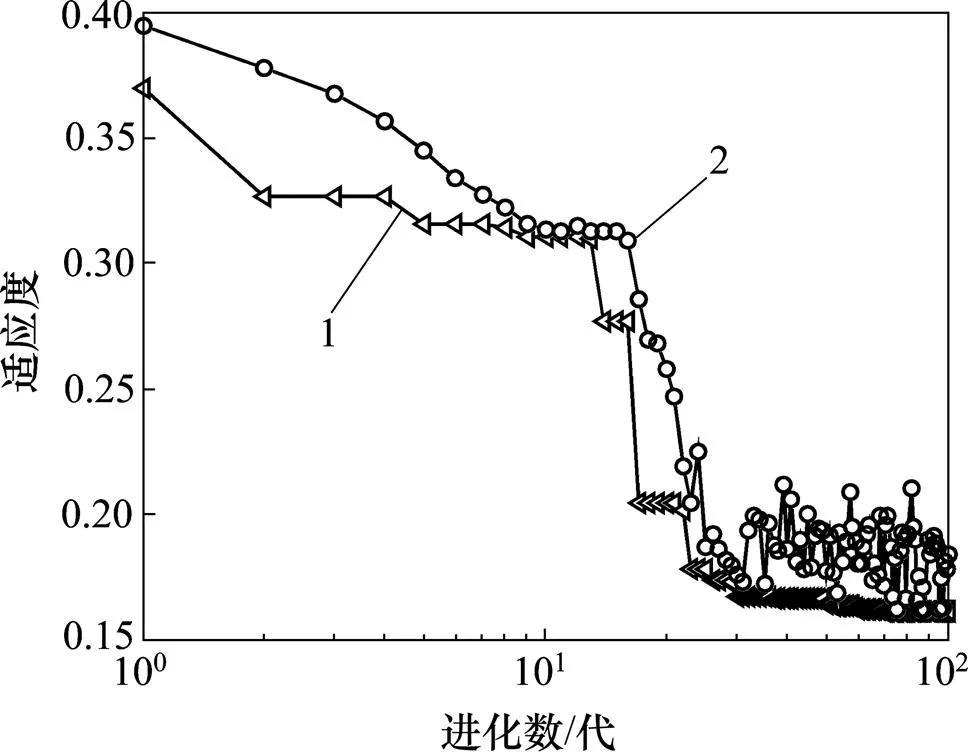
1—最佳适应度;2—平均适应度

1—原始值;2—GA-SVM预测值

图7 测试集最大裂缝宽度模型回归预测结果对比
从图4~6及表3和表4可以看出:本文建立的SVM分类与回归模型对地采诱发建筑物损害效应预测效果良好,评估结果与实际结果吻合,可以很好地对建筑物损害等级进行准确判断。由此可见:将GA与SVM结合起来不仅能发挥SVM的泛化能力,而且使SVM具有更强的学习能力;用SVM理论进行地采诱发建筑物损害效应评估完全可行,比较客观地反映了地采诱发建筑物损害效应的真实情况。在工程实际中,根据本模型确定其损害程度,判定建筑物的补偿形式和补偿标准,使得建筑物补偿工作更加科学合理。GA是以群体为基础,能同时从不同点获取多个极值,因而,得到的解是全局最优的,但它难以单独、有效地作为一种控制方法进行研究。支持向量机的特点是基于结构风险最小化原则,具有很强的泛化能力,而且求解的是1个凸二次优化问题,从而保证了找到的极值解就是全局的最优解且具有唯一性,避免了陷入局部最小的风险,有效地解决了维数灾难问题,但对影响其性能的支持向量机参数及其核函数参数的选取问题还没有完善的准则可以参考。遗传算法对于寻优问题有很强的自适应优化搜索能力,因此,将遗传算法与支持向量机相结合不仅能发挥SVM的泛化能力,而且使SVM具有更强的学习能力。
4 结论
1) 提出基于SVM理论的地采诱发建筑物损害效应预测方法,综合考虑地质采矿方面和建筑物本身方面因素,选取10个影响砖混结构建筑物采动损害程度的因素作为模型的输入,将砖混结构建筑物的损害等级及建筑物的最大裂缝宽作为模型的输出,建立了地采诱发建筑物损害效应预测的SVM分类和回归预测模型。
2) 为提高预测模型的泛化能力和预测精度,应用GA选择SVM的模型参数,以大量建筑物采动损害的工程实例作为学习样本和测试样本进行训练与检验,结果与工程实际结果相吻合。可见将GA与SVM结合起来不仅能发挥SVM的泛化能力,而且使SVM具有更强的学习和外推能力。
3) SVM本身具有很强的非线性映射能力、优秀的自学习和推广预测功能,且具有较强的容错能力和抗干扰能力。随着对地采诱发建筑物损害机理认识的不断深入,采用本文建议的SVM预测模型可以很方便地考虑更多特征因素并对其进行评价。此外,由于GA-SVM预测模型是建立在已发生损害的建筑物观测数据与特征规律学习基础上,因此,学习样本的数量及代表性对地采诱发建筑物损害效应预测判别的准确性非常重要。在学习样本范围外的预测判别可能会产生较大的误差,所以,在实际工程中应根据各自的实际情况,合理选择样本数量及种类才能获得可靠的预测结果。
[1] 刘影, 王旭东. 地下开挖对临近建筑物损害影响评估综述[J]. 地下空间与工程学报, 2008, 5(4): 841−847. LIU Ying, WANG Xudong. Overview of the assessment on the damage from underground excavating on adjacent buildings[J]. Chinese Journal of Underground Space and Engineering, 2008, 5(4): 841−847.
[2] Selby A R. Tunneling in soil-ground movements and damage to buildings in Workington, UK[J]. Geotechnical and Geological Engineering, 1999, 17(3/4): 351−371.
[3] 史秀志, 周健, 崔松, 等. 露天采矿爆破振动对民房危害预测的DDA 模型及应用[J]. 中南大学学报(自然科学版), 2011, 42(2): 441−448. SHI Xiuzhi, ZHOU Jian, CUI Song, et al. Distance discriminant analysis model and its application for prediction residential house’s damage against blasting vibration of open pit mining[J]. Journal of Central South University (Science and Technology), 2011, 42(2): 441−448.
[4] 边亦海, 黄宏伟. 深基坑开挖引起的建筑物破坏风险评估[J]. 岩土工程学报, 2006, 28(S): 1892−1896. BIAN Yihai, HUANG Hongwei. Risk assessment of building damage induced by deep excavation[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(S): 1892−1896.
[5] Najjar Y, Zaman M. Numerical modeling of ground subsidence due to mining[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1994, 30(7): 1445−1452.
[6] Burland J B, Worth C P. Settlement of buildings and associated damage[C]// SOA Review, Conference of Settlement of Structures. Cambridge, London: Pentech Press, 1974: 611−654.
[7] Finno R J, Voss F T, Rossow E, et al. Evaluating damage potential to buildings affected by excavations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(10): 1199−1210.
[8] Son M, Cording E J. Estimation of building damage due to excavation-induced ground movements[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(2): 162−177.
[9] 于广明, 杨伦. 采动建筑物破坏程度预测及破坏机理的研究[J]. 阜新矿业学院学报, 1992, 1(1): 41−45. YU Guangming, YANG Lun. Estimation of damage degree of building and structures due to mining subsidence and the study of damage mechanism[J]. Journal of Fuxin Mining Institutes, 1992, 1(1): 41−45.
[10] 国家煤炭工业局. 建筑物、水体、铁路及主要巷道保护煤柱留设与压煤开采规程[M]. 北京: 煤炭工业出版社, 2000: 1330−1334. China Coal Industry Bureau. Mining rules of left protective coal column for buildings, water, railway and main tunnel[M]. Beijing: China Coal Industry Publishing House, 2000: 1330−1334.
[11] LIAN Chuanjie, LIU Limin. Fuzzy mathematical evaluation for masonry structure buildings’ damage grade caused by coal mining[J]. Journal of Coal Science & Engineering (China), 1999, 5(1): 33−37.
[12] 郭文兵, 刘义新, 李小双. 采动影响下建筑物损害程度的模糊聚类分析[J]. 采矿与安全工程学报, 2007, 24(3): 288−292. GUO Wenbing, LIU Yixin, LI Xiaoshuang. Fuzzy clustering analysis of mining induced damages of buildings[J]. Journal of Mining & Safety Engineering, 2007, 24(3): 288−292.
[13] 刘立民, 刘汉龙, 连传杰. 建筑物采动损坏等级评定的物元模型及其应用[J]. 煤炭学报, 2004, 29(1): 17−21. LIU Limin, LIU Hanlong, LIAN Chuanjie. Matter-element model for building’s damage grade evaluation and its application caused by mining subsidence[J]. Journal of China Coal Society, 2004, 29(1): 17−21.
[14] Gunn S R. Support vector machines for classification and regression[J]. ISIS Technical Report, 1998, 14(1): 5−16.
[15] Kennedy J, Eberhart R C. Particle swarm optimization[C]// IEEE International Conference on Neural Network. New York: IEEE Press, 1995: 1942−1948.
[16] ZHOU Jian, LI Xibing, SHI Xiuzhi. Long-term prediction model of rockburst in underground openings using heuristic algorithms and support vector machines[J]. Safety Science, 2012, 50(4): 629−644.
[17] Cherkassky V, Ma Y. Practical selection of SVM parameters and noise estimation for SVM regression[J]. Neural Networks, 2004, 17(1): 113−126.
[18] Boscardin M D, Cording E J. Building response to excavation- induced settlement[J]. Journal of Geotechnical Engineering, ASCE, 1989, 115(1): 1−21.
[19] Rankin W J. Ground movements resulting from urban tunneling: Predictions and effects[C]// Engineering Geology of Underground Movements. London, 1988: 79−92.
[20] 王金庄, 邢安仕, 吴立新. 矿山开采沉陷及其损害防治[M]. 北京: 煤炭工业出版社, 1995: 158−167. WANG Jinzhuang, XING Anshi, WU Lixin. Protection and treatment of settlement induced by mining engineering[M]. Beijing: Coal Industrial Press, 1995: 158−167.
(编辑 陈灿华)
Model of nonlinear SVM with GA to estimate building damage due to mining-induced ground movements
JIANG Chengrong1, PENG Pingan2, WANG Liguan2
(1. School of Resources and Environment Engineering, Panzhihua University, Panzhihua 617000, China;2. School of Resources and Safety Engineering, Central South University, Changsha 410083, China)
Considering that the evaluation of the effects of builting structures damaged by mining of many factors are not deterministic, nonlinear and has multiple linear features, a new method of the support vector machine (SVM) to predict the effects of the structures damaged by mining was proposed based on the statistical learning theory and the actual characteristics of the project. Considering the geological mining and building factors, ten large factors affecting buildings damage of brick and concrete structure were selected as the proposed model input variables, the damage level of the brick and concrete structure buildings as well as structures of the largest crack width were taken as the proposed model output values. Twenty-two typical cases of buildings and structures damaged by mining were used for training data by introducing radial basis function (RBF) kernel function. For enhancing the generalization performance and prediction accuracy, genetic algorithms (GA) were applied to select parameters for SVM model, thus the damage level prediction of building GA-SVM classification and the maximum crack width with GA-SVM regression model were established,respectively, and another six group cases were sentenced to distinguish samples for further study of the effectiveness and practicality of the proposed model. The results show that the establishment of support vector machine classification and regression model prediction of the effects of building structures damaged by mining can achieve high accuracy, which coincides with the actual results.
underground excavation; building damage; damage evaluation; support vector machine; genetic algorithm; forecast
10.11817/j.issn.1672-7207.2015.09.029
TD229
A
1672−7207(2015)09−3368−09
2014−12−04;
2015−03−04
国家高技术研究发展计划(863计划)项目(2011AA060407);“十一五”国家科技支撑计划项目(2006BAB02A02);国家自然科学基金资助项目(50774092) (Project(2011AA060407) supported by the National High Technology Research and Development Program of China (863 Program); Project(2006BAB02A02) supported by the National Science and Technology Pillar Program during the 11th “Five-year” Plan Period; Project(50774092) supported by the National Natural Science Foundation of China)
彭平安,博士研究生,从事数字矿山研究;E-mail: ping_an@outlook.com
