静压支承导轨密封边的油膜特性

叶仪，殷晨波，贾文华，周玲君



静压支承导轨密封边的油膜特性

叶仪1，殷晨波1，贾文华2，周玲君1

(1. 南京工业大学车辆与工程机械研究所，江苏南京，211816；2. 南京工程学院机械工程学院，江苏南京，211167)

基于理论分析，研究静压支承系统中静压油垫的承载力和刚度特性。利用Coons曲面法建立壁面粗糙形貌符合高斯分布的油膜三维模型，采用数值模拟手段从微观的角度分析粗糙度对密封边油膜性能的影响。研究结果表明：设计参数o存在1个理论最优值使得油垫承载刚度达到最大。受粗糙度影响，油膜压力分布呈现随机波动性。油膜承载力与流动速度保持线性增加关系，但随厚度的增加逐渐降低，降低幅度不断减小。相对粗糙度越大油膜承载力越高，且承载力的增加量几乎不受油膜厚度变化的影响，而流动速度变化时，承载力的增加表现为变化率基本相等。

静压支承；油膜；承载力；刚度；粗糙度

随着工业轻合金材料的广泛应用及加工手段的不断发展，机床的定位精度即将告别微米时代而进入亚微米时代，超精密数控机床正在向纳米进军，未来 10 a内，精密化将成为机床的重要发展趋势。作为核心零部件之一的支承导轨，其性能直接影响机床的定位精度和工作效率，因此如何提高支承导轨的工作性能成为亟需解决的关键问题之一。静压支承导轨通过导轨面间的静压承载油膜(称为静压油垫)将被支承部件浮起，形成纯液体润滑，从而具有诸如摩擦和发热损耗小、润滑和减振性能好、不存在低速“爬行”现象、运动精度高、受外载影响不大等优点[1−3]，非常适合用作精密机床的支撑导轨。因此，油垫的特性(如承载力、刚度)直接决定了静压支撑导轨的工作性能，深入研究其结构参数的影响及油膜流动规律能够有效的指导设计工作。本文作者针对矩形静压油垫，理论分析使承载刚度达到最大值的临界条件，并通过数值模拟的手段从微观的角度研究静压油垫导轨工作面粗糙度对静压油膜性能的影响。

1 承载力与刚度分析

承载力和刚度是静压支承导轨的2项基本性能指标，承载力是指油垫所能平衡的外载荷；刚度则是油垫抵抗外载荷变动的能力，只有刚度满足要求时，才能保证导轨运行的精度和稳定性。

1.1 矩形静压油垫承载能力分析

图1所示为静压油垫压力分布。图1(a)所示为矩形静压油垫的几何结构平面图，液压油通过进口阻尼器降压后导入油垫内的静压腔，并在经过节流密封边时产生一定的压降，使静压腔保持高压，提供平衡负载的承载力。密封边处压力油膜的厚度属于微米级，远小于静压腔的深度，计算时静压腔内部的压力视作等压分布，密封边内的油膜为平板缝隙流动，压力分布呈线性规律，得到图1(b)所示的油垫压力分布。

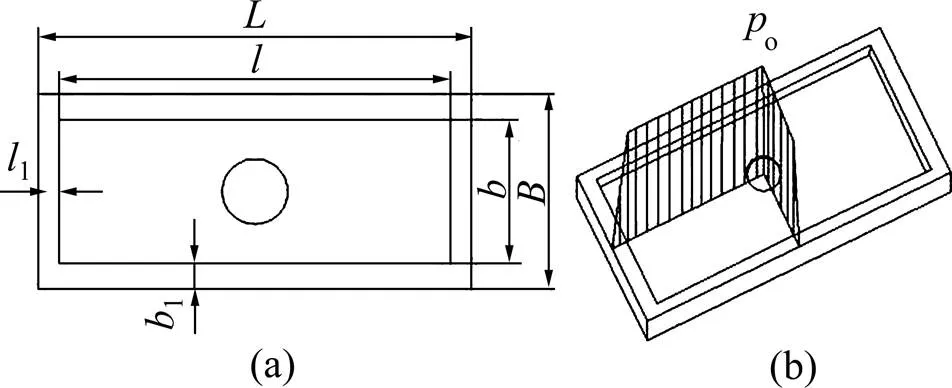
(a) 几何结构；(b) 压力分布

在此假设下，油垫的压力分布为轴对称，通过积分运算可得到静压油垫的承载力：

(1)

式中：o为静压腔压力；和分别为矩形油垫的长度和宽度；和分别为静压腔的长度和宽度。忽略较小项(−)(−)/6，则简化为

有效承载面积为静压腔面积与油垫面积的均值，且承载力与承载面积、静压腔压力呈正比。

1.2 矩形静压油垫承载刚度分析

假设油液为不可压，并且不计黏温效应。油液在进入静压腔前要经过阻尼器降压以获得足够的静压力,此处的液压阻力k可由小孔节流公式变换得到

式中：为油液密度；为油液流量；d为流量系数；d为小孔面积。

油液流出静压时要经过密封边，此处的流动为典型的平行平板缝隙流，不考虑密封边内外在尺寸上的微小差异，且以密封边出口处的压力为参考压力，由缝隙流理论可得密封边液阻ho表达式

其中：为油液运动黏度；o为设计状态下密封边处油膜的厚度。从式(4)可以看出：随着厚度的增加，密封边液阻急剧减小。考虑油液从定量泵出口到流出静压腔的过程中压力的变化，将式(3)和式(4)代入下式可得设计状态下油源压力p与静压腔压力o之间关系：

(5)

为简化表达式，令k与ho的比为设计参数o。外部负载发生变化时，油膜厚度随之变化，在变化过程中定量泵出口s与压油腔压力o可用以下3个关系式表述：

；

式中：ot为负载变化时系统液阻；为负载变化时液阻比。将式(5)和(6)联立，可以得出关于s/o的方程为

求解此方程，s/o的值必定大于0，因此得到o/s的表达式为

将式(8)代入到式(2)，由此得到矩形静压油垫承载力的表达式为

承载刚度定义为引起油膜单位厚度变化时所需提供承载力的变化量，即

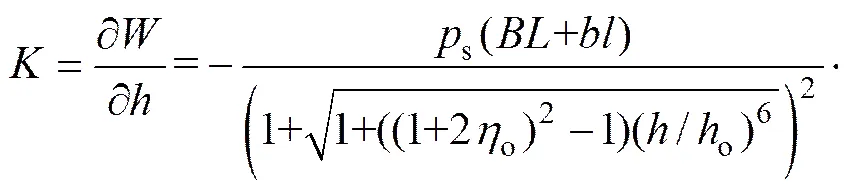
(10)

式中：负号为负载的增加对应油膜厚度的减少，为负载变化时油膜的厚度，可以表达为

将式(11)代入式(10)，得到以油膜厚度相对变化量形式表达的承载刚性

(12)

当外负载很小时，即引起的油膜厚度的变化量Δ远远小于油膜厚度的设计值o时，认为Δ<<1，可以得到设计状态下的矩形静压油垫刚度表达式

由式(13)可知：在设计状态下静压油膜的承载刚度与泵出口压力s，矩形油垫总面积，静压腔面积与油垫面积的比值成正比，而与设计参数o和设计状态下密封边处油膜的厚度o成反比，即∝(s)，∝()且∝(1oo)。

在静压支承导轨设计中，总是以静压油垫能够保持被支承件与导轨面间的纯液体润滑状态为目标，即使是在外载荷发生剧烈变化的工况下。这就要求在油垫几何外形尺寸大致确定情况下，对静压设计中所涉及的参数集合进行组合优化，使得在设计状态下其油膜刚度能够取到极值点max，即把问题转化为求解设计参数η是否存在最优值使得最大。对式(13)求一阶导数ddo

从式(14)可知：d/do=0处的点为所求的油膜刚性极值点，易得满足设计状态下矩形静压油垫承载刚度达到最大值的参数o最优值为

由以上分析可知：要使静压油垫承载刚度取到理论设计上的最大值，在设计时就应该使设计参数o(,,,,o,odd)的值尽可能的接近理论最优值ooptimal。

2 油膜流动特性分析

静压支承油膜的厚度一般为0.015~0.060 mm，已属于微尺度流动的研究范畴，表面力与体积力的比约为常规尺度的上万倍，表面效应大大强化，表面粗糙度在微小体中起重要作用，使流体表现出的流动行为明显区别于宏观流动。已有研究[4−5]表明：当表面粗糙度与油膜厚度处于同一数量级时，粗糙度对油膜特性的影响不可忽视。静压支承油膜的流动特性决定了整个系统的承载力和稳定性，而现有的研究多集中在油垫形状优化、油膜厚度最佳控制、动力学分析等[6−12]，较少考虑粗糙度因素，缺乏基础性研究，因此，有必要就粗糙度对油膜流动的影响进行深入研究。

机械加工表面是由微小的间距和峰谷组成的复杂微观几何形状，细节形貌丰富，具有一定随机性，因此如何准确的表征表面粗糙度的规律特征一直是研究热点。Bahrami等[13]使用高斯分布来描述表面粗糙形貌，建立了粗糙微圆管内充分发展层流流动的一维理论模型，成功预测了流动阻力随相对粗糙度增加的变化趋势。基于以上研究，本文将高斯分布引入到静压支承系统导轨工作面粗糙度的表征中，并提出使用coons曲面造型法建立边界面粗糙高度服从高斯分布的流体模型，采用数值模拟的方法，研究封油边内油膜的流动特性。

2.1 模型建立

假设在直角坐标系中有4个点P(X, Y,Z)，1, 2, 3和4(如图2所示)，为简化复杂表面，将和方向的间距固定，只考虑方向(轮廓高度)的随机性，4点间关系如下：

；

式中：∆和∆分别为和方向上的增量；为轮廓表面基准高度；为粗糙表面轮廓峰值；θ为高斯分布随机数。

令θ服从均值为，标准差为的高斯分布，即θ~N(，2)，表示为

图2 空间4点及构造的coons曲面

本文提出使用双三次coons曲面片的方法来拟合封油边内油膜的边界面，通过构造若干微小的曲面片来拼接组成复杂的表面。空间4个非共面点生成单个coons曲面片的简要步骤(如图3所示)为：依次连接相邻2点，创建4条线性边界；利用Hermite基函数构造4条边界曲线；将相对的边界曲线沿线性边界完成超限插值，分别构造曲面片；利用布尔运算叠加两曲面片即可获得所需coons曲面片。

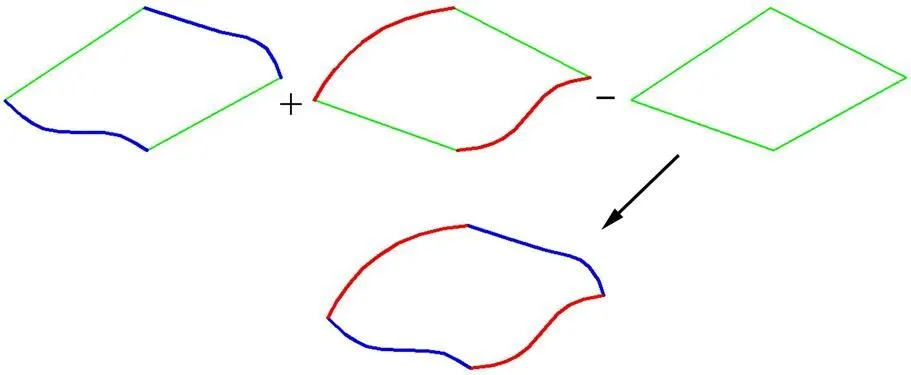
图3 coons曲面片构造步骤

微流动研究中，往往不是所有几何尺寸都处于微尺度之下，相对于油膜的厚度来说，封油边的外形尺寸是很大的宏观量，为更有针对性的研究粗糙度对油膜流动的影响，有必要简化宏观尺寸。截取1小段封油边作为研究对象，简化为10≤厚≤60 μm，宽=300 μm，长=1 600 μm的平板间缝隙流动模型，其中上下表面粗糙且具有相同粗糙度，侧面均为光滑面。设置长、宽向的间距∆和∆为4 μm和3 μm，则油膜的上下粗糙面均被划分成了4×104个小单元，每个单元的4个角点由，θ和确定，对所有单元重复使用双三次coons曲面片并将所有单元拼接，即构造了粗糙表面，如图4所示。

通过控制峰值高度，可以获得不同的粗糙度值。为保证导轨良好的运动精度，静压支承系统在工作中要始终保持相对运动导轨面间的纯液体摩擦状态，因此对导轨面的粗糙度有一定要求：

2≤1/3(18)

在此范围内，调整，建立4种粗糙程度的模型，采用相对粗糙度来表征导轨面的粗糙程度，分别为0，3.33%，6.67%和10.00%，定义为轮廓最大高度与水力直径D的比值，即α=2R/D。

图4 模型粗糙表面

2.2 数值计算

静压支承封油边内的油膜流动处于层流状态，且在计算中不考虑温度，屏蔽能量方程，对所建立的模型作如下假设：稳态层流；忽略重力影响；边界无滑移；忽略黏性耗散。用于求解的连续性方程和动量方程矢量形式为：

式中：为动力黏度；为速度矢量。

计算中使用46号液压油为工作介质，其密度=896 kg/m3，取参考温度30℃时的动力黏度= 0.062 kg/ms，系统为定量供油，施加速度入口条件。整个油膜模型的网格划分在hypermesh软件中完成，在油膜厚度方向上使用贝尔曲线分布网格，使得在接近粗糙面的过程中逐渐加密网格，保证边界处获得高精度的解。采用控制容积有限差分法和SIMPLE算法对控制方程进行求解，求解精度10−6。

对所有仿真模型均采用不同精度的网格进行独立性检测，确保所得到的数值解都独立于网格密度，最终确定的网格数为1.66×105。

2.3 结果与分析

2.3.1 压力分布

图5 所示为入口流速均为5 m/s时，4种模型计算后的上壁面处压力分布，从左至右对应为相对粗糙度依次减小的情况。从图5可知：壁面越粗糙所需提供的入口压力越高，油膜泄压的趋势也越快。此现象表明，粗糙度的出现会增大封油边的液阻，使整体压力上升，保压性能逐渐增强，继而引起油腔承载力的提高。

此外，从图5局部放大图可以看出：光滑模型的沿程压力线性减小，各处压力均匀变化，等压线保持光滑；而粗糙度的出现，使得壁面压力不再遵循严格的均匀变化，而呈现出一定的波动性，等压线也变得杂乱，且随着相对粗糙度的增加而愈发剧烈。这是因为粗糙模型的壁面轮廓高度由高斯分布随机产生，导致波峰波谷的分布具有随机性，当油液掠过粗糙表面的波峰时，会在其背面产生一定程度的漩涡，在波谷处形成背压，引起局部压力的突变，从而使得局部压力分布出现一定的随机性波动性。

图5 粗糙表面油膜压力分布

2.3.2油膜承载力的影响分析

图6所示为油膜承载力随厚度的变化。从图6可以得出：在纯液体润滑前提下，随着油膜厚度的增加，油腔承载力逐渐降低，且降低幅度不断减小，并逐渐趋于恒定。此外从图6还可以发现：相对粗糙度会引起承载力的增大，在油膜厚度较小时，这种影响相对于厚度变化引起的承载力变化可以忽略不计。然而，随着油膜厚度的增加，这种影响越来越显著，比较相对粗糙度最大与光滑的2种情况，在=10 μm时，引起承载力的提高仅为1.67%，而当增加到60 μm时，增量达到了28.67%，不可忽略。

油膜流动速度也会对油腔承载力产生影响。图7所示为油膜厚度=30 μm油膜承载力随流速的变化情况。从图7可见：随着流动速度的增加，油腔压力逐渐升高，并且呈现线性关系，但壁面粗糙度情况的不同会导致承载力受到流速的影响程度也不同，相对粗糙度越大油膜承载力的上升幅度也越大。=10.00%时的承载力相比光滑通道时的承载力提高了10.33%。

α/%: 1—10.00; 2—6.67; 3—3.33; 4—0

α/%: 1—10.00; 2—6.67; 3—3.33; 4—0

油膜承载力随相对粗糙度的变化如图8所示。从图8可见：在油膜厚度和速度一定时，承载力均随着相对粗糙度的增加而提高，且增幅逐渐变大。对比分析2种条件下承载力的变化趋势，不难发现图8(a)所示的曲线近似保持平行，不同厚度下由粗糙度引起的承载力增量相等；而在不同速度下，相对粗糙度引起的承载力变化率基本相等，当为3.33%，6.67%和10.00%时，承载力相较光滑模型近似分别提高了1.5%，5.3%和10.3%。从图8可知：从提高油膜承载力角度出发，使工作表面具有适当的相对粗糙度可以得到比光滑情况下更好的油膜承载效果。但从导轨润滑特性考虑，相对粗糙度过大必然会导致避上下壁面间最薄油膜厚度减小，当静压支承系统工作在重载时，导轨间的纯液体摩擦状态极易被破坏，会引起金属间干摩擦，从而造成振动、冲击，大大降低系统的性能。因此，在设计时，必须在保证导轨始终处于纯液体润滑前提下，使工作面具有一定的相对粗糙度。

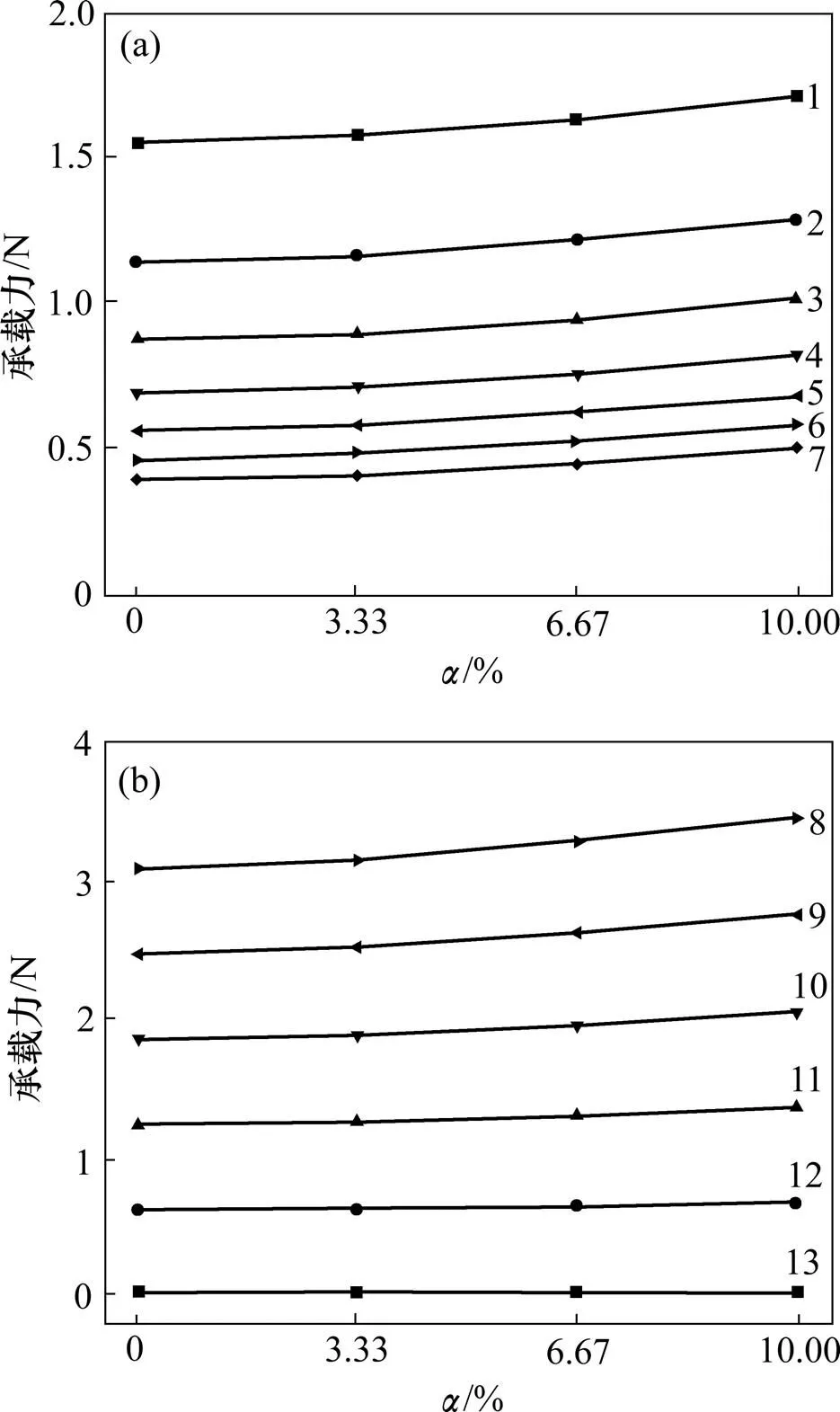
(a) 厚度；(b) 流速

/μm: 1—30; 2—35; 3—40; 4—45; 5—50; 6—55; 7—70/(m∙s−1): 8—10.0; 9—8.0; 10—6.0; 11—4.0; 12—2.0; 13—0.1

图8 油膜承载力随相对粗糙度的变化

Fig. 8 Carrying capacity of oil film changed with relative roughnesses

3 结论

1) 矩形油垫的承载力可以等效近似为油液等压分布在静压腔与油垫平均的面积区域上，设计时要在保证静压力的情况下，尽可能地扩大静压腔的范围。

2)设计集合参数o存在理论最优值ooptimal，使得静压油垫承载刚度最大。

3) 受壁面粗糙度的影响，工作面的压力分布呈现出一定的随机波动性，并随着相对粗糙度的增加而更加剧烈。

4) 在纯液体润滑前提下，油膜承载力随厚度增加而降低，且幅度不断减小，并逐渐趋于恒定；并与流动速度呈现线性增加的关系。

5) 相对粗糙度增加会引起承载力提高，在油膜厚度变化时，表现为承载力增量近似相等，随着厚度增加，影响越发显著；而流动速度变化时则表现为承载力变化率基本相等。

[1] 陈燕生.液体静压支承原理和设计[M]. 北京:国防工业出版社, 1980: 1−50. CHEN Yansheng. Principles and design of the hydrostatic bearing[M]. Beijing: National Defence Industry Press, 1980: 1−50.

[2] 温诗铸, 黄平. 摩擦学原理[M]. 北京: 清华大学出版社, 2008: 25−75. WEN Shizhu, HUANG Ping. Tribology principles[M]. Beijing: Tsinghua University Press, 2008: 25−75.

[3] 于晓东.重型静压推力轴承力学性能及油膜态数值模拟研究[D]. 哈尔滨: 东北林业大学机械学院, 2007: 1−50. YU Xiaodong. Research on numerical simulation of oil film state and mechanics properties of heavy type hydrostatic thrust bearing[D]. Harbin: Northeast Forestry University. College of Mechanical Engineering, 2007: 1−50.

[4] 刘赵淼, 王国斌, 申峰. 基于Navier滑移的油膜缝隙微流动特性数值分析[J]. 机械工程学报, 2011, 47(21): 104−110. LIU Zhaomiao, WANG Guobin, SHEN Feng. Numerical analysis of oil film flow in micro gap with navier slip boundary conditions[J]. Journal of Mechanical Engineering, 2011, 47(21): 104−110.

[5] 刘赵淼, 逄燕. 不同压力差下微通道尺寸和表面粗糙度对摩擦系数的影响[J]. 工程力学, 2012, 29(5): 200−205. LIU Zhaomiao, PANG Yan. Influences of size and roughness of microchannels on friction factors under different pressures[J]. Engineering Mechanics, 2012, 29(5): 200−205.

[6] 邵俊鹏, 张艳芹, 李永海, 等. 大尺寸椭圆形静压轴承油膜态数值模拟[J]. 哈尔滨理工大学学报, 2008, 13(6): 117−120. SHAO Junpeng, ZHANG Yanqin, LI Yonghai, et al. Numerical simulation of oil film state of large size ellipse hydrostatic bearing[J]. Journal of Harbin University of Science and Technology, 2008, 13(6): 117−120.

[7] 杜巧连, 张克华. 动静压液体轴承油膜承载特性的数值分析[J]. 农业工程学报, 2008, 24(6): 137−140. DU Qiaolian, ZHANG Kehua. Numerical analysis of load-bearing capacity of oil film for hydro-hybrid bearing using finite element method[J]. Transactions of the Chinese Society of Agricultural Engineering, 2008, 24(6): 137−140.

[8] 张杰, 郭宏升, 牛犇, 等. 水润滑高速动静压滑动轴承数值模拟[J]. 农业机械学报, 2008, 39(6): 159−162. ZHANG Jie, GUO Hongsheng, NIU Ben, et al. Numerical simulation study on water-lubricated hydrostatic journal bearings[J]. Transactions of the Chinese Society of Agricultural Machinery, 2008, 39(6): 159−162.

[9] 刘红彬, 牛荣军, 薛玉君, 等. 表面纹理对径向滑动轴承油膜承载能力的影响[J]. 润滑与密封, 2010, 35(7): 18−22. LIU Hongbin, NIU Rongjun, XUE Yujun, et al. The effect of surface textures on loading capacity of journal bearing lubricating film[J]. Lubrication Engineering, 2010, 35(7): 18−22.

[10] 姚华平, 黄平. 平行运动的粗糙表面润滑承载性能研究[J]. 摩擦学学报, 2008, 28(2): 150−154. YAO Huaping, HUANG Ping. Load carrying capacity of parallel movement lubricated rough surfaces[J]. Tribology, 2008, 28(2): 150−154.

[11] 叶红玲, 郑小龙, 沈静娴, 等. 液体静压导轨转台轴向振动的动力学建模与分析[J]. 工程力学, 2012, 29(3): 218−225. YE Hongling, ZHENG Xiaolong, SHEN Jingxian, et al. Dynamic modeling and analysis of axial vibration of the hydrostatic slide turntable[J]. Engineering Mechanics, 2012, 29(3): 218−225.

[12] Sharma S C, Jain S C, Bharuka D K. Influence of recess shape on the performance of a capillary compensated circular thrust pad hydrostatic bearing[J]. Tribology International, 2002, 35: 347−356.

[13] Bahrami M, Yovanovich M M, Culham J R. Pressure drop of fully developed, laminar flow in rough microtubes[J]. Journal of Fluids Engineering, 2006, 128: 632−637.

(编辑 罗金花)

Characteristics of oil film between sealing sides in hydrostatic support slideway

YE Yi1, YIN Chenbo1, JIA Wenhua2, ZHOU Lingjun1

(1. Institute of Automobile and Construction Machinery, Nanjing University of Technology, Nanjing 211816, China;2. School of Mechanical Engineering, Nanjing Institute of Technology, Nanjing 211167, China)

Based on theoretical analysis, carrying capacity and stiffness characteristics of oil pad in hydrostatic support system were investigated. A three-dimensional model of oil film with profile of rough surfaces in accordance with Gaussian distribution was established by using Coons surface method. The effects of roughness on characteristics of oil film between sealing sides were numerically simulated from the microscopic perspective. The results show that the designed parameterohas a theoretical optimal value which can make the oil pad bear stiffness to reach the maximum. The pressure distribution of oil film fluctuates randomly under the influence of the roughness. The carrying capacity of oil film increases approximately linearly with flow velocity, but gradually decreases with the increase of the thickness, and the magnitude of decrease reduces continuously as well. Carrying capacity increases with the increase of relative roughness, and the effect becomes more and more distinct. More specifically, the increase of carrying capacity is equal. Additionally, the increase of the carrying capacity remains almost invariable with the change of the thickness, and the increase rates of carrying capacity under different flow velocities are nearly equal.

hydrostatic support; oil film; carrying capacity; stiffness; roughness

10.11817/j.issn.1672-7207.2015.09.014

O357.1；S275.6

A

1672−7207(2015)09−3260−07

2014−12−13；

2015−02−20

国家自然科学基金资助项目(50875122)；江苏省科技支撑项目(BE2011187)；江苏省普通高校研究生科研创新计划资助项目(CXZZ13_0432) (Project(50875122) supported by the National Natural Science Foundation of China; Project(BE2011187) supported by the Science and Technology Support Project of Jiangsu Province; Project(CXZZ13_0432) supported by the Ordinary University Graduate Student Scientific Research Innovation Projects of Jiangsu Province)

殷晨波，教授，从事流体力学和液压系统控制研究；E-mail: yinchenbo@njtech.edu.cn