磁场全张量测量计算方法与误差分析

刘超波，王 斌，陈金刚，代佳龙，孟立飞，肖 琦

（北京卫星环境工程研究所，北京 100094）

0 引言

物体内部磁源产生的磁场会在外部磁场空间中引起磁异常，利用磁异常求取产生磁异常的磁源体几何和磁性参数的过程简称为磁异常的反演解释[1]。磁异常的表征参数主要有磁场标量、矢量和张量。与磁场标量和矢量相比，磁场全张量元素受环境磁场的影响小，能够很好地描述磁源的磁化方向和几何形态，提高对磁源的分辨率[2]。通过磁场全张量数据能获得更多的反映场源特点与细节的信息，这对解释磁异常十分重要，因此磁场全张量探测技术日益得到重视[3-4]。

目前，对磁场全张量的研究与应用主要集中在 航空磁测、海洋磁测等领域，利用组合式梯度计进行大面积探测，基线距离（相邻矢量磁场测量点间隔）较远。磁场全张量的另一个应用方向是用于物体内部多磁源的反演[5]，磁场探测面积较小，基线距离一般为毫米级。基线距离不同，磁场全张量探测方式和误差也会有所不同，需要深入研究。同时，随着航天器长寿命、高可靠要求的提高，空间磁环境效应研究的重要性日显突出[6]。为了能够更加有效地探测航天器内部的磁性分布，有必要研究物体内部多磁源反演技术，因此对小面积磁场全张量测量方法的研究十分关键。

本文针对多磁源反演所需的小面积磁场全张量探测问题，从磁场探测器布局方式出发，提出一种有效的磁场探测方式，比较两种最优的全张量计算数据结构，并分析基线距离对磁场全张量计算的影响。

1 磁场全张量

若空间某处磁感应强度B= (Bx,By,Bz)，则该点处的磁场全张量为

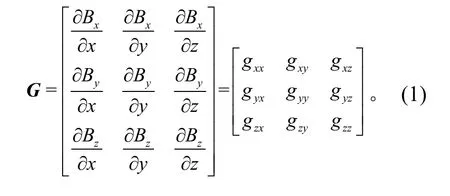
根据Maxwell 方程，在无源的空间，磁场散度和旋度为0，G为对称矩阵，其迹为0，也即gxx+gyy+gzz= 0，gxy=gyx，gxz=gzx，由此可知，磁场全张量G的9 个元素中只有5 个是相互独立的[7]。

2 扫描式磁场测量方法

物体周围空间中大量点处的矢量磁场和磁场全张量数据是多磁源反演所需的基本磁性数据[5]。磁场全张量是根据矢量磁场分布，按照某种数据结构进行计算得到的。

快速获得空间大量点处磁场数据的方式有很多种，最简单的方式是使用一个磁场探测器逐点测量，因而需要较长的测量时间，并且数据不是并行采集，容易受到环境干扰。还有一种方式是采用大量磁场探测器同时测量所有测量点，此方式虽用时较短，但是由于探测器本身的尺寸原因，磁场梯度的基线距离较大，导致梯度值测量误差较大。

基于以上考虑，本文选用了多探测器步进式连续扫描、并行采集的磁场探测方式，简称扫描式探测方式，其原理如图1所示。利用m×n个三轴矢量磁场探测器组成磁场探测器阵列，为了减小时域环境磁场干扰，采取并行方式采集；为了减小振动对磁场探测器的影响，所有磁场探测器位置均固定不变，通过移动被测物体的方式实现空间磁场的采集。

磁场探测器阵列中的m值和n值，也即探测器个数和布局，可以根据被测物体包络尺寸、测量周期、梯度基线距离等不同要求进行调整。扫描式磁场探测方式的优点有2 个：一是可以通过调整被测物体的移动距离实现磁场梯度基线的任意调整；二是部分磁场数据是并行采集，缩短了数据采集时间，减小了空间磁场干扰的影响。

图1 扫描式磁场探测示意图Fig.1 Schematic diagram of scan mode for magnetic field detection

3 磁场全张量计算结构分析

3.1 六面体结构与十字形结构

磁场全张量的标准数据计算结构为六面体结构，如图2所示，其中P1～P7 为磁场测量点，d为基线距离。

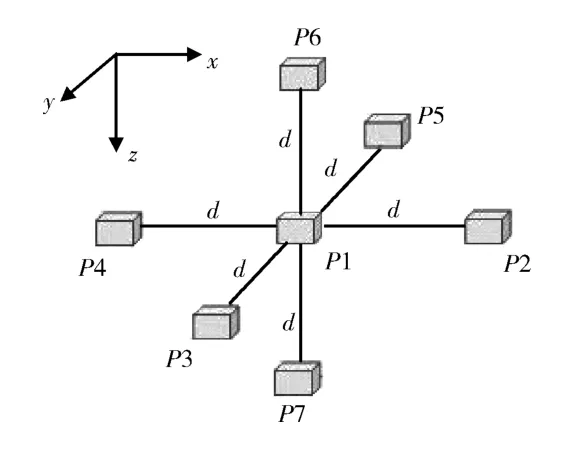
图2 六面体结构示意图Fig.2 Schematic diagram of hexahedron structure

对于六面体结构，磁场全张量的计算公式为

在许多关于磁场梯度全张量计算的实际应用中，考虑到探测和计算的方便，经常利用磁场全张量只有5 个独立元素这个性质简化磁场梯度张量的数据计算结构。简化的数据结构有很多种，比较典形的有正三角形结构、正四面体结构、十字形结构、直角四面体结构以及正方形结构，其中效果最优的是十字形结构[8]（如图3所示），其中P1～P5为5 个磁场测量点，d为基线距离。

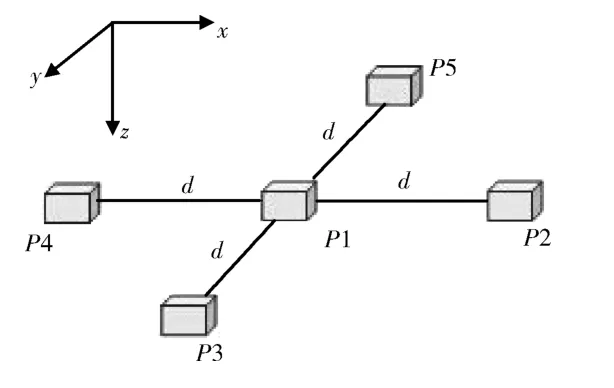
图3 十字形结构示意图Fig.3 Schematic diagram of crisscross structure

对于十字形结构，可根据式(2)、式(3)、式(6)、式(8)和式(9)计算出gxx、gxy、gyy、gzx和gzy，然后根据磁场全张量的性质推导出gyx、gxz、gzz和gyz。

由于扫描式磁场测量能够得到非常密集的矩阵式磁场分布值，所以十字形结构和六面体结构皆可用于磁场全张量的计算。但是，对于任何一种数据结构，在计算磁场全张量时都以差分近似代替了微分近似，而这种近似会在张量值的计算上带来误差。下面将对六面体结构和十字形结构的计算误差进行分析，并与磁场全张量理论值进行比较。

3.2 两种结构的误差分析

3.2.1 随机磁源在固定点的误差

假设包络尺寸为0.3 m×0.3 m×0.3 m 的正方体内部有3 个磁源，利用MATLAB 随机生成每个磁源的磁矩和位置并计算出每个点处的磁场全张量理论值；然后计算出空间固定点(0.48 m, 0.48 m, 0.48 m)处利用六面体结构和十字形结构计算得到的磁场全张量值，基线距离d设为3 mm；最后利用式(11)计算磁场全张量计算值与理论值间的误差δ。对15 组不同的磁源进行了计算，其误差结果见图4。

式中：i和j分别轮流代表x、y、z；gc-ij、gt-ij分别为磁场全张量9 个元素的计算值和理论值。

图4 随机磁源在固定点处的磁场全张量计算误差Fig.4 The computation error of the magnetic full tensor of a random magnetic source at a fixed point

由图4可以看出，对于15 组随机产生的磁源，使用六面体结构和十字形结构计算的磁场全张量的误差基本相等，且最大误差均小于10%。

3.2.2 固定磁源在不同点的误差

假设上述正方体中的3 个磁源的磁矩和位置固定，磁矩分别为(0.5, 0.4, 0.3)、(0.9, 0.7, 0.4)和(0.2, 0.1, 0.5)，单位为A·m2；位置分别为(0.2, 0.1, 0.15)、(0.1, 0.22, 0.11)和(0.15, 0.05, 0.15)，单位为m；基线距离d= 3 mm。利用六面体结构和十字形结构分别计算其周围空间中随机产生的15 个点处的磁场全张量值，并与理论值进行比较，结果如 图5所示。

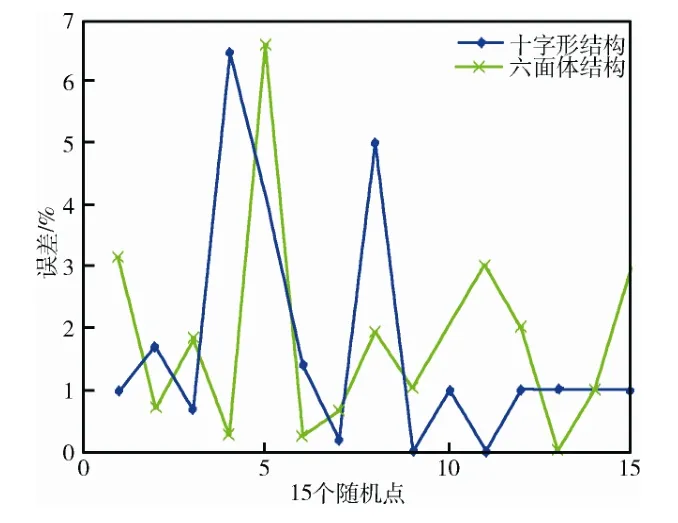
图5 固定磁源在随机点处的磁场全张量计算误差Fig.5 The computation error of the magnetic full tensor of a fixed magnetic source at a random point

从图5可以看出，对于一组固定的磁源，在15 个随机产生的点处，使用六面体结构计算磁场全张量的误差与利用十字形结构计算磁场全张量的误差非常相近，并且最大误差均小于7%。

4 基线距离对磁场全张量的计算的影响

使用与3.2.1 节相同的方法，利用MATLAB 随机产生3 个磁源，设定不同的基线距离值，利用十字形结构计算在两个固定点(0.48, 0.48, 0.48)和(0.36, 0.36, 0.36)处的磁场全张量值，并与理论值进行比较，结果见图6。

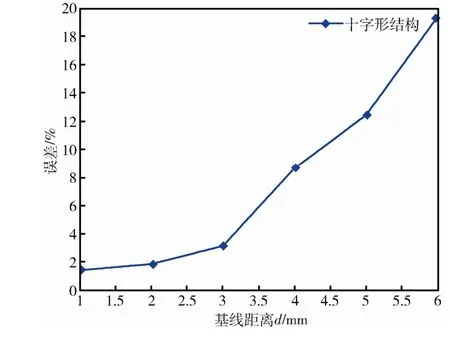
图6 不同基线距离的全张量计算误差Fig.6 The computation error of the magnetic full tensor for different baseline lengths

从图6可以看出，计算误差随着d的增加显著变大，在d小于3 mm 时，其误差值小于5%；在d为4.5 mm 时，误差已经达到了10%左右。由此可见，在计算磁场全张量时，基线距离d是一个非常重要的参数。

5 结束语

在本文中，针对小型物体内部多磁源反演需求，提出了矩阵式连续扫描的空间磁场分布探测方式。对两种最优的磁场全张量计算结构（六面体结构和十字形结构）进行误差分析和比较，结果表明，与理论值相比，两种计算结构的误差相近，且均不大于10%；通过设定不同基线距离，分析了基线距离对磁场全张量计算的影响，结果表明，基线距离对磁场全张量计算具有较大的影响，其误差随着基线距离的增加而增加。考虑到计算的方便性，在通过扫描磁场数据计算磁场全张量时，优先选取十字形数据结构进行计算。

另外，通过本文可以看出，同一数据结构在不同点处或针对不同磁源，磁场全张量的计算误差相差较大，同时两种数据结构的计算误差也不尽相同。因此，下一步有必要对这些因素进行深入研究，找出其特点和规律，指导以后的实际工程应用，不断提高磁场全张量探测精度。

（References）

[1]管志宁.地磁场与磁力勘探[M].北京∶地质出版社, 2005∶257-262

[2]Pedersen L B, Rasmussen T M.The gradient tensor of potential field anornalies∶some implications on data collection and data processing of maps[J].Geophysics, 1990, 55(12)∶1558-1566

[3]Schmidt P W, Clark D A.The magnetic gradient tensor∶its properties and uses in source characterization[J].The Leading Edge, 2006, 25(1)∶75-78

[4]Foss C.Improvements in source resolution that can be expected from inversion of magnetic field tensor data[J].The Leading Edge, 2006, 25(1)∶81-84

[5]陈俊杰, 易忠, 孟立飞, 等.基于欧拉方法的多磁偶极子分辨技术[J].航天器环境工程, 2013, 30(4)∶401-406 Chen Junjie, Yi Zhong, Meng Lifei, et al.Multi-dipole discrimination technology based on Euler inverse method[J].Spacecraft Environment Engineering, 2013, 30(4)∶401-406

[6]齐燕文.空间磁环境模拟技术[J].航天器环境工程.2005, 22(1)∶19-21 Qi Yanwen.Space magnetic environment simulation technology[J].Spacecraft Environment Engineering, 2005, 22(1)∶19-21

[7]张朝阳, 肖昌汉, 阎辉.磁性目标的单点磁梯度张量定位方法[J].探测与控制学报, 2009, 31(4)∶44-48 Zhang Chaoyang, Xiao Changhan, Yan Hui.Localization of a magnetic object based on magnetic gradient tensor at a single point[J].Journal of Detection &Control, 2009, 31(4)∶44-48

[8]谢启源.弱磁物体矢量探测系统研究[D].南京∶南京航空航天大学, 2012∶22-30