面向异构多核处理器的的循环分块

李雁冰，赵荣彩，赵 博，黄品丰

（1.信息工程大学，河南 郑州450001；2.数学工程与先进计算国家重点实验室，河南 郑州450001）

0 引 言

异构多核处理器给高性能计算提供了巨大的潜力，也同时给编程提出了更大的挑战。解决编程问题，首先要有简单易用的编程模型。近些年来，面向异构系统的编程模型发展迅速，出现了一大批并行编程模型［1］。其中，Nvidia等4家公司联合发布的OpenACC［2］受到了广泛关注。目前，OpenACC在GPU 平台上已经取得了很好的效果［3］。但在把OpenACC用于异构多核处理器时，操作大量数据的代码不能获得很好的加速。原因是异构多核处理器中加速器的设备内存空间有限，代码访问的数据量过大时，无法一次性将所需数据加载到设备内存。当程序运行过程中设备内存失效，会由加速器发起直接存储器访问 （direct memory access，DMA），从主存读入所需数据到设备内存，而这个时延通常是巨大的。针对这一问题，本文对OpenACC进行扩展，引入了循环分块子句，对循环进行分块处理，使得每个循环块中的数据能够存储在设备内存中。

循环分块是提高传统处理器Cache上访存效率的有效方法［4］，也可以用于提高异构多核处理器的性能。但是二者之间有一些差别，针对Cache的循环分块只需要考虑如何使Cache中的数据尽可能多地得到重用。而在异构多核处理器上，不但需要考虑循环如何分块，还需考虑数据的分块问题，即设备内存容量对数据分块大小的限制。使用分块技术来优化数据的传输是异构系统上编译优化技术的研究热点。比如，文献 ［5］提出了一种基于参数模型的长流分段技术；文献 ［6］提出了结合循环分块、数组分块技术与区间着色数据布局技术的优化方法。这些分块方法，需要通过分析程序的数据依赖关系对循环进行分块变换，只能处理可置换循环，且实现难度大，不能充分利用原有循环结构的局部性［7］。本文引入的循环分块子句用于指示编译器，将循环的迭代空间按照指定的分块大小进行分割，划分给加速线程 （其作用类似于OpenMP［8］中的schedule子句），分块过程不需要进行数据依赖关系的分析和程序变换，更加简单易用，而且不改变原有循环的结构，保证了原有循环结构的局部性。

要将已有的大量串行程序改写成OpenACC并行程序并非易事，使用自动并行化技术［9］将串行程序自动变换成适合异构系统的OpenACC并行程序，是获得OpenACC 并行程序的一条有效途径。因此，本文提出了一个针对异构多核处理器的循环分块子句自动生成算法，并在基于Open64开发的面向异构多核处理器的 “源－源”自动并行化系统Auto－ACC中进行了实现。

1 异构多核处理器

异构多核处理器是在一个芯片内集成了多个不同结构或功能的处理器核，一般包含通用主处理和加速器。异构多核处理器可以使用不同类型的处理器核来完成不同类型的任务，如任务并行度较高，则使用众多精简的加速器提速，否则用强大的通用主处理器运行。这比用相同的处理器核执行所有任务更有效率，更利于提高处理器的性能。其典型代表有索尼、东芝和IBM 公司联合开发的Cell处理［10］，ClearSpeed公司的CSX600处理器，AMD 的Fusion APU，Stream Processors公司的storm－1处理器等。

其中Cell处理器的结构如图1所示，一个Cell芯片上包含 一 个PowerPC 处 理 单 元PPE （powerPC processing element）和8个协同处理单元SPE （synergistic processing element）。PPE 上 有 一 个PowerPC 核 心 和L1、L2 两 级cache，SPE支持类AltiVec的向量指令，并且有256KB的局部存储器LS。PPE负责SPE上计算任务的调度。SPE在计算时只能访问自身的LS，LS和主存Memory之间的数据传输通过互连网络EIB （element interconnect bus）和访存控制 器MIC （memory interface controller）使 用DMA 方式实现。

通常，异构多核处理器的主处理器包含有容量较大的主存，加速器包含设备内存。设备内存占用的芯片面积更少，功耗更低，访问速度更快，但容量有限，往往无法满足使用大数组的科学计算程序的存储需求。大部分数据存储在主存，设备内存失效时必须通过DMA 操作完成主存与设备内存的数据传输。然而DMA 操作开销较大，DMA次数过多会大大降低程序性能。因此提高设备内存空间利用率，减少DMA 次数，是发挥异构多核处理器性能的关键。

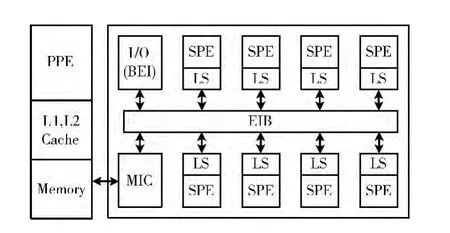
图1 Cell处理器结构

2 循环分块子句的引入

为了让OpenACC能够更好地发挥异构多核处理器的计算优势，尽量克服异构多核处理器存储方面的弱点，本节对OpenACC进行扩展，引入了循环分块子句block。block子句对循环的分块信息进行说明，指导编译器将循环按照指定的分块大小进行分割，同时将循环对应的数据按照同样的块进行分割。

下面给出block子句：

（1）语法：

block （index1：blocksize1，index2：blocksize2，...）

index1、index2等为嵌套循环从外到内的各层索引变量，blocksize1、blocksize2等为该层的分块大小。某一层不需要分块时，其索引变量和分块大小省略不写。block子句作为loop构造的可选子句，使用时必须出现在loop构造的子句列表中。

（2）说明：

block子句对循环各层进行分块，循环在执行时各层只能以指定的块大小划分给加速线程，并且循环引用的数组对应的各维也按照同样的块大小进行分割。恰当的分块方案则能使各数组的数据块加载到设备内存，并且每个加速线程执行的循环块有良好的数据局部性。

（3）示例：

block子句指示对该嵌套循环第1层 （i－循环）以块大小为1的方式划分，第2层 （j－循环）以块大小为3的方式划分，第3层 （k－循环）不划分。同时，数组A 的第1 维也以块大小为1的方式划分，第2维以块大小为3的方式划分；数组B的第1维以块大小为3的方式划分。

下面说明block子句针对该示例，指导编译器进行循环分块的过程。

第1步：对第1层 （i－循环）以块大小1进行划分，得到100个循环块，其中第m （m＝1，2，…，100）块为：

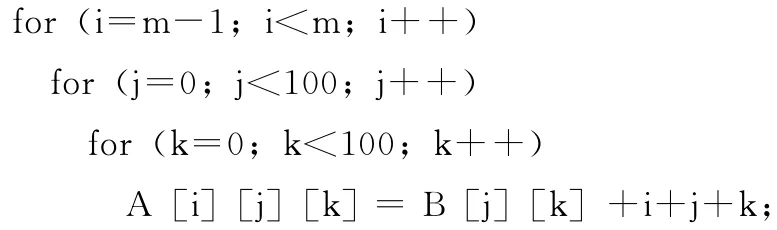
每个循环块仍是3层嵌套循环，第1层迭代量为1，第2、第3层同原循环。

第2步：对上一步得到的100个循环块的第2层 （j－循环）以块大小3进行划分，每个循环块又被划分为34个小块，除最后一小块第2 层的迭代量为1，其它为3。其中，第1次分块得到的第m 个循环块第2次划分以后的第n （n＝1，2，…，34）个块记为第 （m，n）块，为：

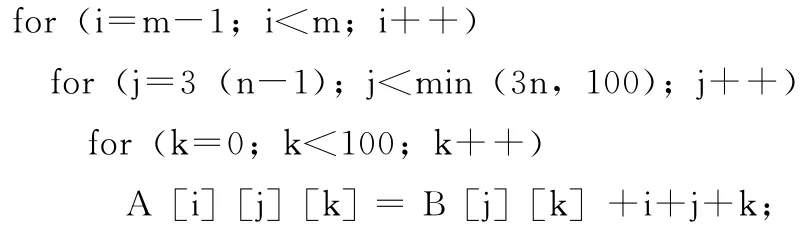
在将循环块加载到加速器执行时，由于第1 层 （i－循环）为并行层，编号的第1维不同的循环块可以按照任意顺序调度执行。第2层循环 （j－循环）只能串行执行，所以第1维相同的循环块第2维数字小的必须先执行。例如第（1，3）、（2，1）块可按任意顺序执行，第 （1，3）块必须在第 （1，4）块之前执行。

每个循环块引用的数据也将是原来数组的一个数据块，循环块引用的数据块会在编译时由编译器分析得到。（数组数据块表示方法为数组名后跟一个方括号，方括号内的起始下标和长度用来指定数组范围，例如a［2：n］表示元素a［2］，a［3］，…，a［2＋n－1］。）第 （m，n）块循环引用的数组A、B的数据块分别为A ［m－1］［3 （n－1）：3］［0：100］、B ［3 （n－1）：3］［0：100］ （当n小于34时）或A ［m－1］ ［99：3］ ［0：100］、B ［99：1］ ［0：100］（当n等于34时）。

这里我们把异构多核处理器中的加速器阵列看做是线性阵列，则循环块、数据块到加速器的映射过程如图2所示。

通常的循环分块方法需要根据程序数据依赖关系，通过进行循环分段和循环交换实现分块，其实现过程复杂而且程序变换可能破坏原有循环结构的局部性，且只能用于可置换循环。而block子句实现的循环分块是在把循环的迭代空间划分给加速线程时，按照指定的块大小进行划分，其划分过程不需要考虑数据依赖关系，也不需要进行程序变换，更加简单易用，而且适用于各种循环结构。

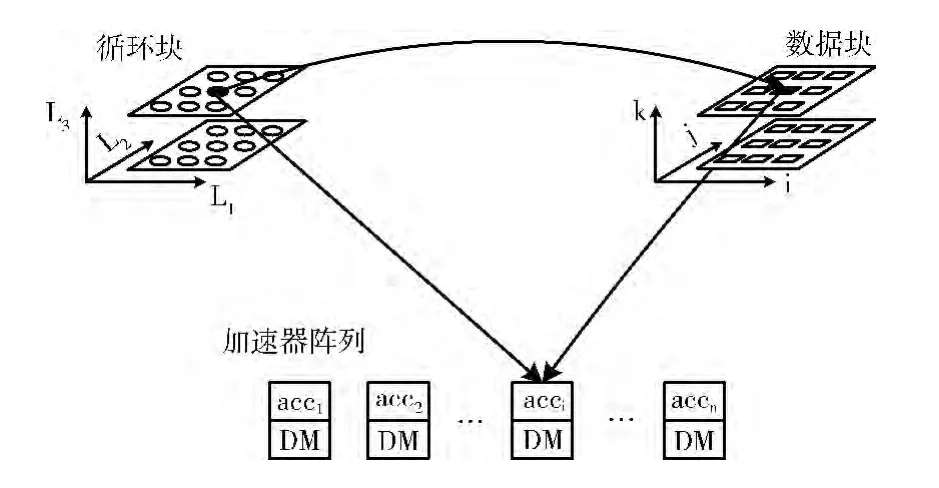
图2 循环块、数据块到加速器的映射

3 循环分块子句生成算法

生成循环分块子句的关键是找到最优的循环分块方案，即在保证循环块所需数据加载进设备内存的同时，尽可能地提高分块后循环块的局部性。对这两个方面分别进行分析：一是构建数学模型描述循环分块和对应的数组分块情况，以便分块方案能够保证循环块所需数据加载进设备内存并且尽可能充满设备内存；二是在分块过程中利用数据重用理论［11］保证分块是有利的，即能够提高程序的局部性。

3.1 问题的数学模型

因为循环分块子句为loop构造的可选子句，其分块的对象为外层可并行执行的嵌套循环。设并行嵌套循环为｛L1，L2，...，Ln｝，其 中L1为 最 外 层 循 环 （即 并 行 循 环层），Ln为最内层循环。循环引用数组Ak（k＝1，2，...，m）的维数为lk，数组元素大小为Sk。设备内存容量为M 。循环嵌套层Li（i，＝1，2，...，n）的分块大小为bi，bi＝0表示该维不分块。如果数组Ak第j（j＝1，2，...，lk）维的下标表达式中含有循环嵌套层Li的索引变量，当Li的分块大小bi≠0时，数组Ak第j维的分块大小d（k，j）＝bi；否则，该维不分 块，则 分 块 大 小d（k，j）＝D（k，j），其 中D（k，j）表 示 数 组Ak第j 维的元素个数。为方便表示，用x（k，j）等于1和0分别表示数组Ak第j 维分块和不分块。

不同数组的数据块加载到设备内存时，其总大小不能超过设备内存容量。于是，循环分块方案的求解问题可以建模为以下最优解问题

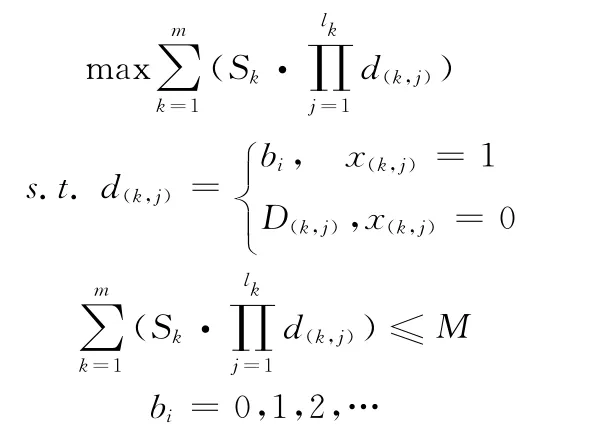
循环分块方案的求解即是求满足条件的向量b＝（b1，b2，...，bn）T，使 各 数 组 的 数 据 块 之 和 所 占 空 间 尽 可 能地大。

3.2 数据重用理论

这里直接引用了文献 ［11］中数据重用相关的部分。一个准确的数据依赖代表两个访问同一内存单元的不同语句实例，因此依赖就可以被看成指示那些经常被重用的存储单元。就这一点来说，程序中越多的依赖意味着越多的重用。

关于循环分块的有利性，有以下结论：

通常，如果在一个非最内层的循环的不同迭代间有重用，则分块是有利的。

在两种情况下，可以得到外层循环的重用：①循环携带一个有小的阈值的任何类型的依赖，包括输入依赖，循环携带依赖；②循环的索引变量出现在一个多维数组的连续维中，而不出现在其它维中。

3.3 算法的具体实现

在实现循环分块子句生成算法时，以3.1 节中的数学模型为基础，计算每一层的分块大小，并利用3.2 节中的数据重用理论决定是否对该层进行分块，以保证对该层的分块是有利的。在循环分块之前，我们已经对循环的次序进行了调整，使得内层循环具有小跨距的访问，以便程序有更好的局部性。嵌套循环的最外层为并行层，对该层划分得到的块将并行地执行，所以需要分块时总是先对最外层进行分块，而且对最外层进行分块得到的分块数不能少于加速部件的数目，否则将造成计算资源的浪费。分块本身会带来一定的调度开销，为减少分块数目，对尽量少的层进行分块。本节基于以上原则设计了分块方案求解算法。

要求解3.1节中模型的最优解较为复杂，这里我们采用了贪心算法进行求解：

首先，令b＝（0，0，...，0）T；

然后，从外到内依次求解循环每一层的分块值，即解向量b的每一维的值。在求解嵌套循环每一层的分块值时，都使该层的分块值是满足约束条件的最大值，及一个局部最优解；

最后，用每一层的局部最优分块值合成整体分块方案最优解的近似解。

一个n层循环嵌套的循环分块方案的求解算法为：

算法：循环分块方案求解算法

输入：并行嵌套循环L＝ ｛L1，L2，…，Ln｝ （L1为并行循环层，且循环次序已做了调整，内层循环具有小跨距的访问），嵌套层数n，设备内存大小M，加速器数目N

输出：循环分块方案b ［n］ （b ［i］为循环Li的分块大小，b ［i］等于0表示该层循环不分块）

3.4 实例分析

本小节通过下面矩阵乘法的核心对循环分块子句生成算法进行说明。

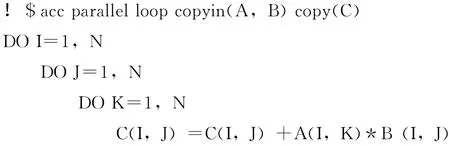
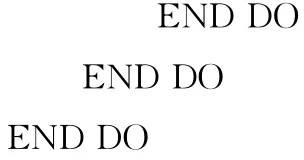
首先我们对循环次序进行调整，使得内层循环具有小跨距的访问，到得的循环如下：

假设A、B、C数组为整型数组，整型数据大小为4字节，设备内存空间为16KB （16384字节），矩阵规模N 为128。循环分块方案求解算法实施过如下：

第1步：计算该循环使用数组的总大小。其值为 （3＊128＊128）＊4＝196608字节，远远超出设备内存空间的大小，必须分块后才能装入设备内存。

第2步：计算最外层循环 （J－循环）的分块大小。由于A（I，K）的自输入依赖，该层具有重用，对该层的分块是有利的。先令该层的分块大小为1，这时数组A 不划分，数组B和C 的第2维也按块大小1划分，3个数组数据块的总大小为 （128＊1＋128＊1＋128＊128）＊4＝66560 字节，超过了设备内存空间的大小。说明对数组该维的最小分块仍会使设备存储空间溢出，需要对下一维进行划分。取该层的分块值为1。

第3步：计算次外层循环 （K－循环）的分块大小。由于对C（I，J）的重用和对B（K，J）的邻接引用，所以K－循环也带有重用，对该层循环的分块是有利的。先令该层的分块大小为1，这时A 数组的第2维按块大小1划分，B数组第1维、第2维都按块大小1划分，C数组仍是第2维按块大小1划分，3个数组数据块的总大小为 （128＊1＋1＊1＋128＊1）＊4＝1028字节，远小于设备内存空间大小。为充分利用存储空间，应增大分块值。当该层的分块值增大到31时，3个数组数据块的总大小为 （128＊31＋31＊1＋128＊1）＊4＝16508，大于设备内存空间，已达到临界值，所以该层分块大小应为30，算法结束。

所以该算法得到的循环分块方案为 （1，30，0），即最外层按块大小1划分，次外层按块大小30划分，最内层不划分。上述矩阵乘法的核心代码段对应的扩展了循环分块子句的OpenACC代码为：

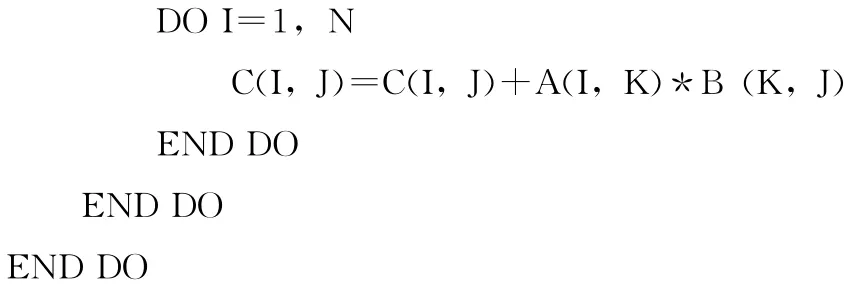
4 实验结果与分析

课题开发的自动并行化系统Auto－ACC 已实现了含有循环分块子句的OpenACC 程序的自动生成。本节使用的测试平台为某国产异构多核处理器构成的计算机系统，该国产异构多核处理器采用主从核结构，由通用处理主核和精简的计算从核组成。单个计算节点包含一个主核和一个从核阵列。从核阵列有64个从核，每个从核运行轻量级操作系统，拥有大小为16KB 的局部存储器。并安装有江南计算所研发的支持OpenACC 扩展规范的编译器JC－ACC。

本节的测试分为3个部分：首先，针对上文中的矩阵乘法测试不同分块方案下的运行时间，验证本文算法求解得到的分块方案是否为最优的分块方案；然后，改变矩阵乘法的规模，验证算法对不同的数据规模是否都能取得好的效果；最后，选择了期权定价模型BlackScholes、spec2000中天气预报建模程序swim 的calc2、雅可比迭代jacobi以及交替方向迭代adi等4个科学计算程序，这4个程序的核心循环主要是对数组的操作，需要大量的设备内存空间，通过比较含有本文算法生成的循环分块子句的OpenACC程序和没有循环分块子句的OpenACC 程序的加速比，验证了本文扩展的循环分块子句及提出的循环分块子句生成算法对异构多核处理器是有效的。

图3给出了针对上文中矩阵乘法在12种不同分块方案下的程序运行时间对比。可以看出本文算法求得的方块方案 （1，30，0）是一个较优的方案，但存在另一较优的分块方案 （2，30，0）。这是因为本文的算法为贪心算法，不能总是求得总体最优解，但本文算法求得的方案十分接近最优解，引起的程序运行时间的差异很小。其中，方案（1，0，0）和 （2，0，0）因分块过大，导致循环块所需数据大部分需要加速器发起DMA 从主存移动到设备内存，运行时间较长。方案 （1，1，0）和 （2，1，0）因为分块太小，导致了过多的调度开销。

图4给出了矩阵乘法在128、256、512和1024这4个规模下，含有本文算法生成的循环分块子句和没有循环分块子句的OpenACC程序的运行时间对比。有循环分块子句的OpenACC程序运行时间和没有循环分块子句的相比，平均加速了6.53倍。其结果表明本文算法对不同的数据规模都能取得好的效果，而且矩阵规模越大，计算量和所需的数据量越大时，加速效果越好。

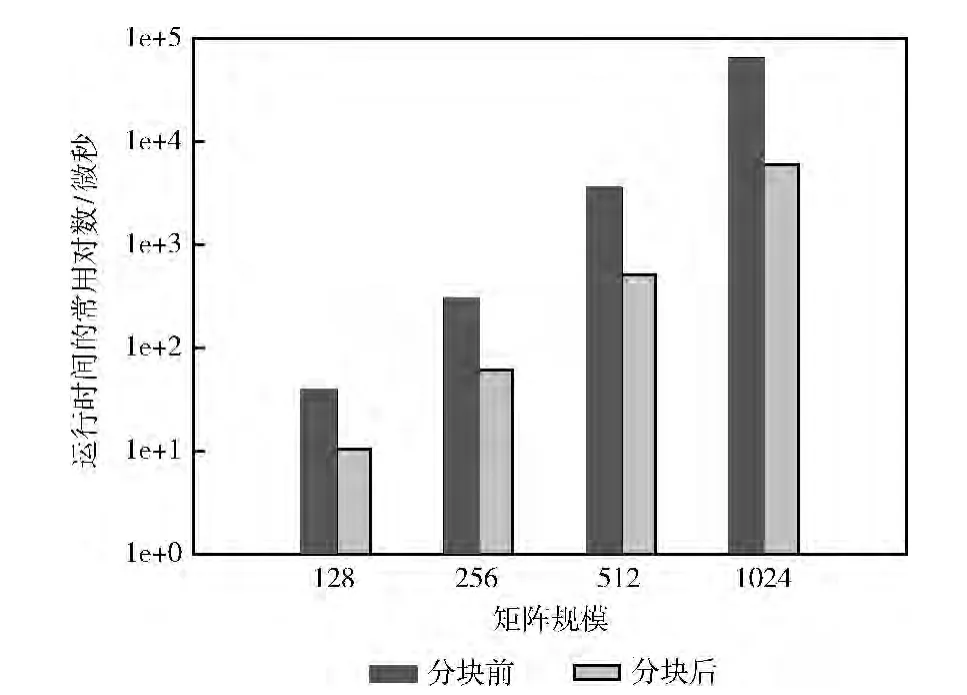
图4 不同矩阵规模分块算法效果对比

图5给出了BlackScholes、calc2、jacobi、adi这4个程序，在带有本文算法生成的循环分块子句的情况下，加速比的提升情况，加速比平均提升2.66倍。其结果表明本文扩展的循环分块子句及提出的循环分块子句生成算法在异构多核处理器上能够对程序进行明显的加速。其中，Black－Scholes的并行循环为单层循环，对其进行分块后无法带来数据重用，所以性能提升不是很明显。而其它3个程序的并行循环为二层或三层嵌套循环的外层循环，对其分块后能带来较多的数据重用，有效减少DMA次数，加速效果明显。

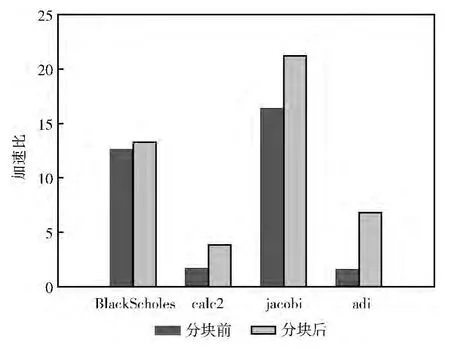
图5 科学计算程序分块前后加速比对比

5 结束语

异构系统的迅速发展亟需一个简单易用可移植的编程模型，人们对OpenACC 寄予厚望，希望它能像OpenMP（面向共享存储结构）一样被广泛使用。目前OpenACC 已经在GPU 上取得了很好的效果，本文所属课题的工作是把OpenACC运用于异构多核处理器，并针对异构多核处理器的特点对OpenACC做了相应的扩展。本文增加了循环分块子句，并给出了一个有效的循环分块子句生成算法。但本文算法没有考虑分块后加速器间的负载均衡等问题，需要进一步的完善。

［1］Duran A，AyguadéE，Badia RM，et al.Ompss：A proposal for programming heterogeneous multicore architectures ［J］.Parallel Processing Letters，2011，21 （2）：173－193.

［2］The OpenACC application programming interface ［EB／OL］.www.OpenACC－Standard.org，2013.

［3］Customer＿Stories［EB／OL］.www.openacc－standard.org，2013.

［4］Bao B，Xiang X.Defensive loop tiling for multi－core processor［C］／／Proceedings of the ACM SIGPLAN Workshop on Memory Systems Performance and Correctness.ACM，2012：76－77.

［5］DU Jing，AO Fujiang，TANG Tao，et al.Parameter model based strip－mining technique on the stream processor ［J］.Journal of Software，2009，20 （9）：2320－2331 （in Chinese）.［杜静，敖富江，唐滔，等.流处理器上基于参数模型的长流分段技术 ［J］.软件学报，2009，20 （9）：2320－2331.］

［6］Li L，Wu H，Feng H，et al.Towards data tiling for whole programs in scratchpad memory allocation ［G］.LNCS 4697：Advances in Computer Systems Architecture.Berlin：Springer Berlin Heidelberg，2007：63－74.

［7］LIU Yong，LU Linsheng，HE Wangquan.Easy data tiling method for software－managed memory hierarchies［J］.Journal of Software，2010，21 （Sl）：290－297 （in Chinese）. ［刘勇，陆林生，何王全.一种面向软件管理内存层次的简易数据分块方法 ［J］.软件学报，2010，21 （Sl）：290－297.］

［8］OpenMP 3.1 specifications ［EB／OL］.openmp.org／wp／openmp－specifications／，2013.

［9］Midkiff SP.Automatic parallelization：An overview of fundamental compiler techniques ［M］.Morgam ＆ Claypool Publishers，2012：1－169.

［10］Chen T，Raghavan R，Dale JN，et al.Cell broadband engine architecture and its first implementation：A performance view［J］.IBM Journal of Research and Development，2007，51（5）：559－572.

［11］Allen R，Kennedy K.Optimizing compilers for modern architectures：A dependence－based approach ［M］.1st ed.California：Morgan Kaufmann Publisher，2001：547－548.