CFD预测不同进风方向对蒸发式冷凝器流场的影响

朱进林 谢 晶 王金锋 杜子峥 周洪剑

（1.上海水产品加工与贮藏工程技术研究中心，上海 201306；2.上海海洋大学食品学院，上海 201306；3.上海宝丰机械制造有限公司，上海 200444）

蒸发式冷凝器是一种集冷却塔与冷凝器，传热和传质过程为一体的高效节能设备。蒸发式冷凝器工作时，冷却水经过顶部的喷嘴均匀地喷淋在冷凝盘管表面，形成一层水膜，温度较低的水膜通过潜热和显热方式带走冷凝盘管内高温制冷剂大部分的热量，从而达到冷凝流体的目的。相比其他冷凝器而言，蒸发式冷凝器具有节能节水、占地面积小、安装维修方便等优点［1］，被广泛用于制冷空调、医疗、化工等领域［2］。蒸发式冷凝器气流的优化对提高冷凝效率有着重要的现实意义。

计算流体力学（computational fluid dynamics，CFD）基于离散化的数值计算方法，可用来分析流体流动、热交换、分子运输以及热传导等一些复杂物理现象。与实际试验相比，CFD模拟具有成本低、不受物理和试验模型限制、灵活性强等优点，能给出完整和详细的数值计算过程［3］。目前CFD计算模拟技术已趋向成熟，广泛应用于各式冷凝器各种场的研究［4－8］。郭常青等［9］利用汽液二维降膜模型，探讨了壁面热流密度、液相进口温度，以及空气流速对板式蒸发冷凝器板面温度的影响。梁治会等［10］对空调用蒸发式冷凝器进行了数值模拟和结构优化，主要研究了喷嘴喷淋速度与安装位置对蒸发式冷凝器换热效果的影响，得出不同设计条件下内部的温度场和速度场分布状况，并提出了优化方案。为了进一步掌握进风因素对换热器流场的影响，刘清明等［11］建立腔内气流流场的数值模型，分析得出双面进风比单面进风更能实现压力场、速度场分布的均匀性。

目前针对蒸发式冷凝器配风量的研究较多，但这些研究［12，13］大多未能深入揭示传热与传质过程机理。本研究拟利用CFD计算软件对蒸发式冷凝器内腔流场开展非稳态数值模拟，以预测蒸发式冷凝器在不同进风风向作用下5s内温度场和气流场的变化情况，从而为以后在蒸发式冷凝器进风风向设计方面提供参考依据。

1 数值模型

1.1 物理模型

本试验研究对象为上海某机械有限公司生产的一款尺寸为1.4m×1.1m×2.5m蒸发式冷凝器。在合理简化冷凝器实物的基础上，建立了蒸发式冷凝器内腔的三维物理模型。

在物理模型中，该模型尺寸为0.250m×0.250m×0.435m，模型底部为集水槽，高度为0.05m，空气进风口设置在模型壁面两侧以及顶部，两侧进风口高度为0.1m，宽度为0.25m，顶部进风口长度为0.125m，宽度为0.25m，盘管部分高度为0.285m，按三角叉排方式排列，共5（排）×5（列）。单根盘管长度为0.25m，外径0.025m，盘管之间横向间距为0.05m，竖向间距为0.05m。空气垂直通风口吹入，与盘管进行换热后从顶部出风口排出。图1为冷凝器单向进风的物理模型。

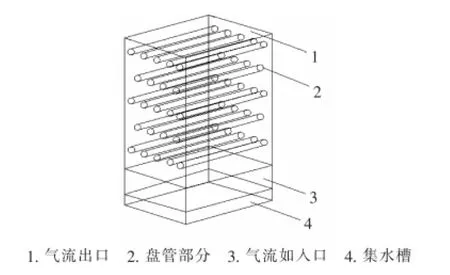
图1 冷凝器单向进风的物理模型Figure 1 Physical model of condenser with single inlet

1.2 CFD模型

运用Fluent自带的Gambit软件对物理模型区域进行网格划分。考虑到冷凝盘管排列方式较为复杂，结构化网格不能满足划分需求［14］，本试验采用较为复杂的TGrid方法划分，在近壁面处进行局部网格加密。在本计算域中设定网格尺寸为5mm，共生成1 277 683个网格，经检验完全满足计算精度需求，对于冷凝盘管部分，网格尺寸同样设为5mm，每个盘管生成7 623个网格。

在计算之前，对上述模型进行进一步简化和假设，认定气流为常温常压下的空气，冷凝盘管壁面温度设为恒定。CFD运算的基本思想是通过求解一系列流动控制方程组来获得流场变量的近似值，具体表现可以体现为连续性方程、动量方程以及能量方程［15］，常用流动与传热问题控制方程［16］：

连续性方程：

X方向动量方程：

Y方向动量方程：

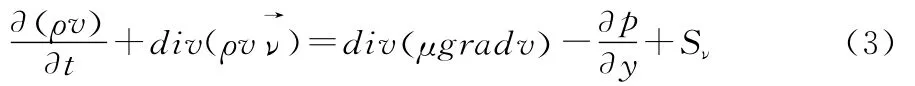
Z方向动量方程：

能量方程：

式中：

ρ——密度，kg/m3；

μ——动力黏度，N·s/m2；

t——时间，s；

T——温度，K；

p——压力，Pa；

k——传热系数，W/（m2·K）；

cp——比热容，J/（kg·K）；

u、v、w——速度矢量的ν→的3个分量，m/s；

Sμ、Sν、Sω——广义源项；

ST——粘性耗散项。

在本试验中，进风空气在风机的强制对流作用下，空气流态从过渡状态充分发展为湍流，雷诺数较大，根据判断标准［17］采用k－ε模型。对于近壁面处需要使用壁面函数处理，在本模拟中选择标准壁面函数。湍流能量输运方程和能量耗散输运方程以及粘性系数［16］：

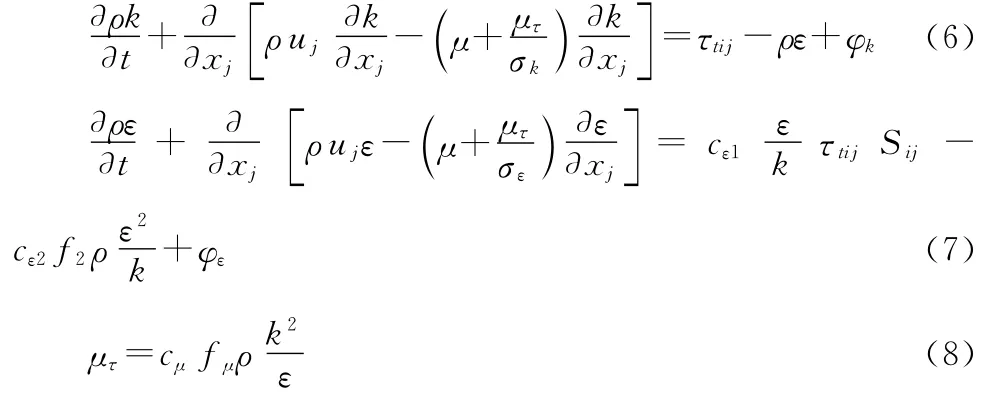
式中：

ρ——密度，kg/m3；

ε——耗散率，m2/s3；

k——湍动能，m2/s2；

μ——粘性系数，N·s/m2；

σk、σε——湍动能k和耗散率ε的湍流普朗特数；

τtij、Sij——粘性模型和平均速度应变率张量；

fμ——近壁衰减函数；

Φk、Φε——壁面项；cμ——默认常数。

［18］，式（6）～（8）中各常数定义为：Cμ＝0.09，Cε1＝1.44，Cε2＝1.92，σk＝1.0，σε＝1.3，Prt＝0.9。

1.3 边界条件

在本试验中需要对建立的物理模型冷凝器的壁面、气流入口、冷凝盘管以及气流出口进行边界设置。冷凝器的壁面按照第二类定热流密度条件设定，冷凝盘管壁面温度设为恒定，温度大小设为313K；冷凝器进风入口按照速度入口设定，速度为0.2m/s，温度为298K，方向垂直进风口，紊流强度设为5%，水利直径按长方形入口计算公式计算分别为0.083m和0.167m；气流出口设为流体出口，无需定义任何内容，此处不考虑水膜对温度及流场的影响。

1.4 计算方法

冷凝器在工作时，由于风机强制循环空气，冷凝器内腔气流处于紊流状态。在本试验中，采用Simplec算法求解压力、速度的耦合，该算法计算精度高，使模拟结果更贴切实际情况［19］。控制方程中各项离散格式选择二阶迎风格式，相比一阶迎风格式，二阶迎风格式具有更小的扩散性，模拟精度更高［20］。松弛因子设置采取默认设置，收敛判断条件为所有物理量的误差小于10－6且出口速度处于平稳状态。

2 数值计算

2.1 稳态模拟

在正常的CFD模拟中，通常默认只有在稳态计算前提下验证了数值模拟的可行性后才能进行下一步计算［21］。本研究中为了确保模型的可行性，对单面进风、双面进风以及双面加顶部组合进风3种方式进行了稳态模拟，并在模型中建立了腔体平均温度以及回流面平均温度监控曲线图。图2为3种风向下，冷凝器稳态状态时的三维剖面温度分布图，剖面位置为z＝0.2，0.3，0.4m 处的XY截面。由图2可知，冷凝器在模拟一定时段后收敛，长度方向温度对称分布，高度方向温度逐渐增加，结合模型监控曲线可以得出，内腔温度以及出风口平均温度都达到了相对稳定，分别维持在302.3K以及303.2K左右，3种进风方式之间略有差距，误差维持在2%以内，这是由于模型设置过程中，对冷凝器外壁以及盘管部分所用材料设置一定热导率和热流密度导致的。模拟计算后的结果显示，本模拟方法较准确可靠，鉴于实际中，冷凝器工作环境为一个非稳态状态，因此有必要对冷凝器做进一步的非稳态模拟。

2.2 非稳态模拟

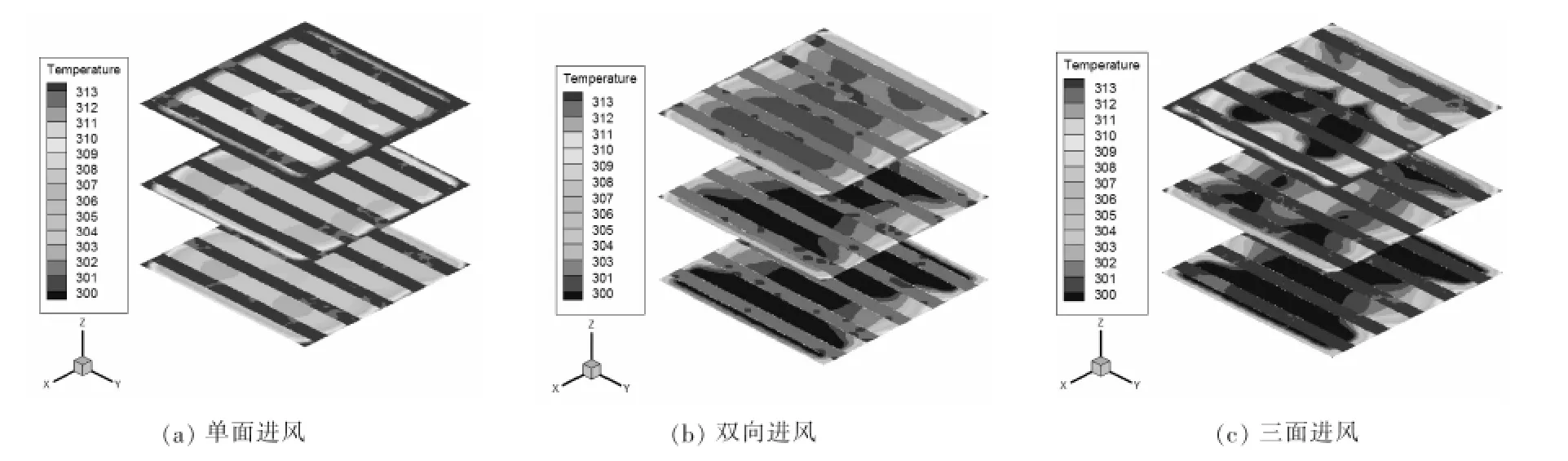
图2 稳态模拟下冷凝器截面（z＝0.2，0.3，0.4m）温度分布Figure 2 Temperature distribution in section of condenser（z＝0.2，0.3，0.4m）under steady state numerical simulation

图3 单向进风0，2，5s冷凝器截面（y＝0.125m）温度分布Figure 3 Temperature distribution at 0，2，5sin section of condenser（y＝0.125m）with single inlet

以稳态模拟的结果作为非稳态模拟的初始条件，对冷凝器进行非稳态模拟运算。图3显示了单面进风冷凝器在运算0，2，5s时的三维温度分布图，剖面图选取y＝0.125m处XZ的截面。比较后发现，单面进风开始时，空气侵入冷凝器内部，靠近进风口处的温度下降较快，空气流速在水平方向逐渐衰减，在流动过程中冷空气与内腔热空气不断发生热交换，在冷热不同密度差的作用下，气流组织逐渐改变了原来的运行轨迹，当冷空气气流组织在到达冷凝器内壁时，与内壁面发生碰撞，近壁面处出现拐角，进而形成漩涡。

图4、5分别显示了冷凝器在单向进风和双向进风2，5s时的空气流场温度、速度以及流场的分布情况。剖面图取z＝0.1m处的XY截面。由图4、5可知，冷凝器在进风时，高度方向0.1m处XY截面处温度场和气流场在长度方向上较为对称，水平方向单面空气入侵速度快于两面进风速度，这是由于两面进风速度方向相对，进入冷凝器气流组织之间相互冲突，减缓了整体吹入速度；双面进风下水平方向温度较为平均，比起单面进风，能够获得温度较为均匀的入口进风，更利于整体降低冷凝器内腔的温度。从2种进风风向速度分布图（图4（f）、5（f））可以发现，单面进风冷凝器内腔中更易出现涡流和死角区域，这是因为比起双面进风，单面进风时内腔空气流速不均匀，气流组织在碰到管壁以及壁面时，运动轨迹发生变化，气流组织分布情况更复杂，易形成较多的涡流；双面进风冷气流组织分布较为对称，流动情况较为简单，涡流的数量降低，且涡流的强度也有所减弱。

图4 单面进风2，5s冷凝器截面（z＝0.1m）温度、速度和流场分布Figure 4 Temperature，velocity and streamline distributions at 2，5sin section of condenser（z＝0.1m）with single inlet

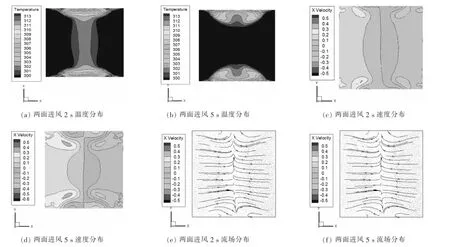
图5 两面进风2，5s冷凝器截面（z＝0.1m）温度、速度和流场分布Figure 5 Temperature，velocity and streamline distributions at 2，5sin section of condenser（z＝0.1m）with double inlets

图6为双向进风时冷凝器内腔高度方向温度变化情况。为方便观察，分别取2，5s时距离冷凝器底部0.2，0.3，0.4m处XY截面温度分布图。从图6并结合图2双向进风稳态时温度分布可以看出，模拟2s时，由于反应时间较短，冷凝器入口气流组织相互冲突，降低了气流进入内腔速度，影响了换热，腔体内部高度方向温度在外界条件变化时略有升高；随着冷空气不断吹入盘管间隙，冷气流在浮力作用下上升，与盘管进行换热吸收热量，内腔温度开始下降，随着冷气流的继续侵入，内腔温度逐渐向稳定发展；盘管弯头与冷凝器外壳之间区域空气流速较小，换热效果较差，与冷凝器盘管间隙温度相比，温度较高。

图7为三面进风时冷凝器在运算0，2，5s时的三维温度分布图，剖面图选取y＝0.05，0.15，0.22m 处的XZ截面。比较三者可以看出，三面进风开始时，冷凝器内腔压力在冷热气流温差作用下压差较大，瞬间进入内腔冷气流较多，内腔温度有所下降，随着时间的推移，侵入的冷气流逐渐增多，三股气流组织汇合，空气与盘管进一步换热，内腔温度慢慢升高，经历一段时间后，内腔温度逐渐达到稳定。

图6 双向进风2，5s冷凝器截面（z＝0.2，0.3，0.4m）温度分布Figure 6 Temperature distribution at 2，5sin section of condenser（z＝0.2，0.3，0.4m）with double inlets

图7 三面进风冷凝器0，2，5s时截面（y＝0.05，0.15，0.22m）温度分布Figure 7 Temperature distribution at 0，2，5sin section of condenser（y＝0.05，0.15，0.22m）with three inlets

2.3 讨论

通过单面进风、双面进风的模拟试验分析，进风速度在水平方向逐渐衰减，发现可以适当增加进风口气流组织的速度，从而缩短冷凝器内腔整体温度达到均匀状态的时间。

单向进风时，冷凝器内腔部分会出现吹风死角，贴近管壁和壁面地方出现较多数量的涡流，双向进风与单向进风相比，可以降低因热流扰动引起的涡流数量以及强度。

水平吹入冷空气，冷凝器高度方向气流组织在长度方向呈对称分布，考虑可以改变进风面积的大小以及进风角度来提高内腔气流场分布均匀性。

三面进风冷凝器在工作初始阶段降温效果较好，可以通过调节顶部与底部进风口进风速度，来进一步提高冷凝器换热效果。

鉴于在本研究中对物理模型进行了合理性假设，以及设定了一系列不同的边界条件，计算模拟与实际测试存在一定的误差，在以后的非稳态模拟中，有必要进一步细化模型，延长模拟计算时长，得出不同风向作用下，冷凝器内腔温度场以及气流场达到均匀时的情况。

3 结论

本试验采用CFD技术模拟了不同风向对蒸发式冷凝器内腔温度场以及流场分布情况，分析对比3种不同风向模拟情况，得出了以下几个结论：

（1）单面进风时，冷凝器内腔下部靠近进风口处空气温度下降较快，冷气流水平侵入冷凝器底部，在密度差作用下逐渐上升与内腔冷凝盘管进行换热；

（2）与单面进风相比，双面进风气流组织在长度方向上分布较为对称，双面进风能够降低气流因管壁和壁面处热流扰动引起的涡流的数量和强度；

（3）三面进风时，冷凝器的内腔温度在三股气流共同作用下，先后经历一个先下降再上升的过程，贴近壁面处，有空气流动死角存在，部分点的局部温度较高；

随着CFD模拟技术在蒸发式冷凝器方面研究的深入，在以后的计算模拟中，可以尝试在特定喷淋水密度的条件下，研究不同进风速度、进风角度以及进风面积对蒸发式冷凝器换热效果的影响。

让我来说一下这个岛。这里叫东极岛，是这个国家最东面的一个岛屿，是这个陆地最遥远的一粒饼干屑，是这只公鸡上最不起眼的一粒鸡米花。太平洋的风率先扑到我们岛上，我的房子矗立在这个岛东边最平坦的泥土上。我的窗口比我的门大，和你们不同的是，我的窗永远打开，只有起风的时候，我才关上；但你们的窗永远关着，只有起风的时候，你们才打开。

参考文献

1 肖志英.提高蒸发式冷凝器效率的途径［J］.河北化工，2007，31（1）：31～33.

2 Manske K A，Reindl D T，Klein S A.Evaporative condenser control in industrial refrigeration systems［J］.Refrigeration，2001，24（7）：676～691.

3 谢晶，吴天.小型冷库门开关过程温度场的数值模拟［J］.上海水产大学学报，2006，15（3）：332～339.

4 Nasr M M，Hassan M S.Experimental and theoretical investigation of an innovative evaporative condenser for residential refrigerator［J］.Renewable Energy，2009（34）：2 447～2 454.

5 Heyns J A，Kroger D G.Experimental investigation into the thermal-flow performance characteristics of an evaporative cooler［J］.Applied Thermal Engineering，2010（30）：492～498.

6 Jahangeer K A，Andrew A O T.Numerical investigation of transfer coefficients of an evaporatively-cooled condenser［J］.Applied Thermal Engineering，2011（31）：1 655～1 663.

7 文娟.基于数值模拟的风冷冷凝器速度场的研究［D］.广州：华南理工大学，2005.

8 董俐言，王宝龙，石文星，等.板式蒸发式冷凝器传热传质的数值模拟［J］.制冷学报，2013，34（1）：10～17.

9 郭常青，朱冬生，蒋翔，等.板式蒸发式冷凝器传热传质的数值模拟［J］.华南理工大学学报，2009，37（3）：53～57.

10 梁治会.空调用蒸发式冷凝器数值模拟与结构优化［D］.长沙：长沙理工大学，2013.

11 刘清明.蒸发式冷凝器流场分析及其应用与空调节能研究［D］.广州：华南理工大学，2010.

12 Gao Sheng-wei，Ren Jing-qiu，Hong Wen-peng.Scheme design and analysis of variable condition of evaporative condenser for steam condensing of steam feeding water pump for 1 000MW air-cooled unit［J］.Energy Procedia，2012（17）：1 177～1 184.

13 钟振兴，朱冬生，刘清明，等.板式蒸发式冷凝器传热性能试验研究［J］.流体机械，2011，39（2）：39，58～61.

14 Foster A M，Swain M J，Barrett R.Experimental verification of analytical and CFD predictions of infiltration through cold store entrances［J］.International Journal of Refrigeration，2003，26（8）：918～925.

15 乔慧芳.蒸发式冷凝器强化传热及强度分析［D］.河南：郑州大学，2008.

16 唐家鹏.FLUENT14.0超级学习手册［M］.北京：人民邮电出版社，2013：15～30.

17 陶文铨.计算流体力学与传热学［M］.北京：中国建筑工业出版社，1991：3～34.

18 陶文铨.数值传热学［M］.西安：西安交通大学出版社，2002：10～40.

19 王新坤，许文博，赵坤，等.基于CFD的多孔管热风数值模拟与设计方法［J］.排灌机械工程学报，2011，29（1）：82～86.

20 缪晨，谢晶.冷库空气幕流场的非稳态数值模拟及验证［J］.农业工程学报，2013，29（7）：246～253.

21 汤毅，谢晶，王金锋，等.CFD预测风机摆设形式对冷库的影响［J］.食品与机械，2012，28（1）：124～128.