OTN中FEC的优化设计及实现

朱 博，孟李林，李小龙，邵瑞瑞

(西安邮电大学计算机学院，陕西西安 710061)

随着通信系统向高速率、高容量方向发展，光传输网络(Optical Transport Network，OTN)得到了广泛应用。OTN是通过G.709等一系列ITU－T的建议所规范的新一代“数字传送体系”和“光传送体系”。但由于信道中光信号的衰减、各路光信号之间的串扰以及色散等原因，不可避免地会产生误码。

在G.709［1］中定义的OTN帧结构采用数据交织与 Reed－Solomon(255，239)码实现 FEC(Forward Error Correction，前向纠错)功能，以此纠正传输中出现的误码。FEC方式与反馈重传纠错方式相比，无需反馈信道，避免了反复重发而延误传输时间。

在G.709定义的OTN中，OTU2的帧结构由4行×4080列组成，每一行的前3 824列作为信息部分，后256列作为校验信息部分。OTN中FEC的实现过程就是在发送端根据前3 824列的数据，利用数据交织和RS编码相结合的方法产生后256列的校验信息，并在接收端根据校验信息最大限度地纠正信号在传输中产生的误码。

根据G.709，研究了OTN中数据交织方法和RS编解码算法，并完成了FEC电路设计。

1 数据交织

采用数据交织的目的是把一个较长的突发差错离散成随机差错，再用纠错码技术消除随机差错。交织的深度越大，则离散度越大，抗突发差错能力也越强。

G.709中采用以1 Byte为单位、深度为16的交织方式。其方法是将OTU2每一行的信息使用字节间插方法拆分成16个子行，每一路编码器或解码器负责处理其中的一个子行［2］。

在发送端，数据交织的过程如图1所示，当帧头指示信号到来时，选择开关打到0，1～8路编码器使能设为有效，并将收到的64位数据 Din［63:0］的低8位Din［7:0］给第 1 路编码器，将 Din［15:8］给第 2 路编码器，以此类推，Din［63:56］给第8路编码器。8路编码器同时工作，当第二个时钟到来时，选择开关打到1，1～8路编码器使能设为禁止，9～16路编码器使能设为有效，数据按上述方法给第9～16路编码电路，之后的节拍依次循环。

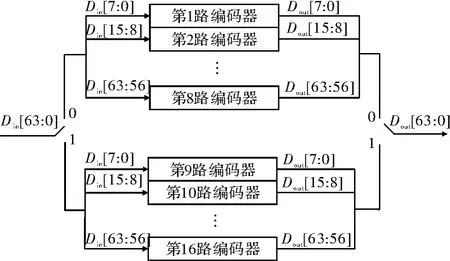
图1 数据交织过程

接收端的数据交织方法与发送端类似，这里不再重复。

2 单路RS编码器设计

在G.709中，采用 RS(255，239)码，即信息数据为239 Byte，校验数据为16 Byte，共255 Byte，纠错能力为8 Byte。

对于RS(255，239)码的编码器，将输入的信息数据以多项式形式表示为m(x)=(m238x238+…+m1x+m0)，其中每个系数均是一个8 bit的码元符号，m238是信息数据的第一位。因为RS码为系统循环码，所以编码后的信息C(x)可表示为C(x)=x16m(x)+r(x)，其中r(x)即校验数据多项式，是x16m(x)除以生成多项式g(x)的余式。编码器可采用LFSR(Linear Feedback Shift Register，线性反馈移位寄存器)电路实现，如图2所示。

图2 编码器电路

图2中“⊗”是有限域乘法器;“⊕”是有限域加法器;R0，R1，…，R15是 m －bit寄存器。当帧头指示信号到来时，计数器从1开始计数，在使能为有效的情况下，每个时钟节拍加1。计数器数值在1～239时，编码电路中的两个选择器均为1，此时编码器的输出即输入;计数器数值在240～255时，选择器为0，此时编码器输入为0，将16个寄存器中的数值依次输出，完成编码过程。

3 单路RS解码器设计

RS解码方法分为时域解码和频域解码，频域解码需要的硬件开销比时域解码多，因此本文只研究时域解码方法。时域解码器结构框图如图3所示。

图3 RS解码器结构框图

RS码的解码过程分为4步:(1)由接收到的信息计算伴随式S(x)。(2)利用S(x)解关键方程得到Λ(x)。(3)利用Λ(x)和步骤(1)计算得出的S(x)，通过Chien搜索算法找到错误位置，并由Forney算法计算出错误数值。(4)更正错误数据并将其输出。

3.1 计算伴随式

定义接收码字多项式R(x)除以码的生成多项式g(x)的余式为伴随式多项式S(x)

根据霍纳(Horner)准则，对于RS(255，239)码，将式(1)改写为嵌套算法

计算电路如图4所示。

图4 伴随式计算电路

初始化时，将16个寄存器全部置0，输入第一个码元符号时，先与寄存器中的零值相加，再经过常数乘法器后和下一码元符号相加，如此循环直到接收第255个码元符号后，就可以得到全部16个伴随式，最后通过选择器依次从16个寄存器中读出数据。

3.2 解关键方程

该模块的功能是根据前一模块得出的伴随式S(x)求解错误位置多项式Λ(x)，是整个译码电路中最复杂也是最耗资源的一个模块。文中采用改进的无逆IBM算法，其步骤是从式(2)到式(7)循环迭代，直到满足 k=15［3］

初始化时，各变量的值为:

式中，k是迭代次数;Δ(k)(x)是待求的错误位置多项式;L(k)是Δ(k)(x)的阶;T(k)(x)和γ(k)(x)是辅助计算的中间变量。

式(2)即为计算Λ(x)和S(x)的卷积和，可以采用FIR滤波器电路实现，如图5所示。

图5 Δ(x)计算电路

3.3 Chien搜索算法

Chien搜索算法的目的是找出错误码元符号的位置，并输出错误指示信号。其方法是将a－i(i=1，2，3，…，254)代入 Λ(x)=1+Λ1x+Λ2x2+… +Λ8x8，若Λ(a－i)=0，则说明接收到的第 i个码元符号出现错误［4］。

图6 Chien搜索电路

3.4 Forney算法

首先根据之前计算得出的S(x)，先计算得出Forney算法所需的Ω(x)。对Ω(x)的计算其实就是计算S(x)和Λ(x)的卷积和，因此，也可采用计算Δ(x)的电路实现。

在计算Ω(x)的电路中，寄存器在初始化时全部置0，之后使16个伴随式依次通过寄存器，当所有伴随式通过寄存器后，便可得到Ω(x)。

图7 纠错电路

设计的解码器延迟为275时钟节拍，因此FIFO的深度设为275。

4 乘法器的设计

从上文中可看出，RS编解码电路中大量用到了有限域乘法器，由于RS码是定义在有限域上的多进制码，因此电路中的乘法器并不是普通的二进制乘法器，其实现较为复杂。本文重点研究基于弱对偶基的比特并行乘法器和标准基乘法器。

4.1 基于弱对偶基的比特并行乘法器

在设计基于弱对偶基的比特并行乘法器时，首先根据式(8)将自然基下的输入b［7:0］变换到弱对偶基下的 b*［7:0］。

在求得对偶基下的系数后，还要求出弱对偶基下的扩展系数，计算公式为

然后根据式(9)计算弱对偶基下的乘法

最后，根据式(10)将计算结果从弱对偶基转化为自然基，完成乘法运算。

基于弱对偶基的比特并行乘法器在实现步骤上比较复杂，需要在乘法器的输入端和输出端加上基变换电路，但其优点是电路结构规整。

4.2 标准基乘法器的设计及优化

标准基乘法器较为直观，根据文献［5］，先将两个因子按多项式乘法相乘得到一个次数不高于14的多项式，再将得到的多项式对生成多项式求模。

值得注意的是，在编码器和伴随式计算电路、Chien搜索电路和Forney算法电路中出现了常数乘法器。对于常数乘法器，由于其中一个因子是固定的，因此可在推导输出与输入因子的关系是直接将常数代入，以乘以59的乘法器为例，59(十进制)=111011(二进制)，用标准基表示为a5+a4+a3+a1+a0，并将输入因子m［7:0］写为

两式按有限域乘法运算法则相乘后，按位整理便可得到乘积q［7:0］与输入因子的关系:

也就是说，乘以59的乘法器只由异或门组合即可实现，大幅降低了电路复杂度。

通过观察不难发现，乘以59的乘法器电路中多次出现了m［7］^m［2］，所以可将其作为一个整体进行运算，当再次出现时便可直接使用。利用这个思想将乘以59的乘法器改写为

通过改写，(m［7］^m［2］)在代码中虽然出现了4次，但在软件综合时，则是将其综合成同一个模块，因此电路可得到进一步优化。

5 设计验证及分析

为验证编码器，在Matlab软件中调用rsenc(msg，n，k)函数，输入数据为238个0，1个1，计算得出的校验数据为 118，52，103，31，104，126，187，232，17，56，183，49，100，81，44，79。图 9 上半部分为编码器的仿真结果，可看出，两者输出数据相同，说明编码器设计正确。

对于解码器，根据编码器结果，将信息数据的后8 Byte改为1，2，3，4，5，6，7，8，其输出结果应为 238 个0，1个1。仿真结果如图9下半部分所示，与预期结果一致。

图8 仿真结果

在QuartusII中，分别对采用弱对偶基乘法器、标准基乘法器以及含有经过优化的常数乘法器的FEC电路，选用Altera CycloneIII EP3C120F780I7系列开发板进行综合，结果如表1所示。结果表明，采用含经优化的常数乘法器的方案占用资源最少，速率最高;本文研究的FEC电路速率均高于167.3 MHz，能够满足OTU2数据流的速率要求。

表1 不同方案综合结果

6 结束语

根据G.709协议，针对OTU2数据流，用数据交织和RS码设计并实现了OTN中的FEC电路。设计中采用数据交织，增大了FEC的纠错性能;还对有限域乘法器的3种实现方案做了对比，选出最佳方案。经过验证，所设计的FEC电路能够高速实现OTN中的FEC功能。所设计的FEC电路已经应用于陕西省“13115”科技创新工程重大科技专项的项目之中。

［1］ITU －T －Recommendation－G.709(version2.0).Y.1331－2003，interface for the optical transport network(OTN)［S］.USA:ITU －T －R －G，2003.

［2］谢军，冯浩，蒋旭.OTN中FEC技术的应用［J］.光通信研究，2005(3):24－27.

［3］顾艳丽，周洪敏.基于FPGA的高速RS编解码器设计与实现［J］.通信与广播电视，2008(1):12－16.

［4］江藤良纯，金子敏信.纠错码及其应用［M］.北京:科学出版社，2003.

［5］俞旋.RS编解码的FPGA实现［D］.南京:东南大学，2008.

［6］韩雪，蒋旭平.RS编解码过程及软件实现［J］.电子科技，2010，23(12):88 －91.