直缝埋弧焊管焊接残余应力的数值模拟*

晁利宁， 毕宗岳， 余 晗， 张晓峰， 鲜林云，张国超， 徐 凯， 梁 航

（1.国家石油天然气管材工程技术研究中心，陕西 宝鸡721008；

2.宝鸡石油钢管有限责任公司 钢管研究院，陕西 宝鸡721008）

直缝埋弧焊管焊接残余应力的数值模拟*

晁利宁1,2， 毕宗岳1,2， 余 晗1,2， 张晓峰1,2， 鲜林云1,2，张国超1,2， 徐 凯1,2， 梁 航1,2

（1.国家石油天然气管材工程技术研究中心，陕西 宝鸡721008；

2.宝鸡石油钢管有限责任公司 钢管研究院，陕西 宝鸡721008）

直缝焊管焊接过程中产生的焊接应力和变形会影响焊管的使用性能和寿命。应用大型通用软件ABAQUS，基于双椭球热源模型，利用“生死单元”技术，模拟了直缝焊管多丝埋弧焊的内外焊接过程，描述了准稳态温度场和残余应力场计算数值及其在整个管体上的分布情况。结果表明，在焊接过程中焊缝附近温度梯度很大，在远离焊缝的地方温度梯度渐渐趋于平缓；随着热源的移动，温度中心也随之移动，最高温度可达母材的熔点。焊后残余应力主要分布在焊缝附近，管体在其他部位应力很小，最大残余应力为528 MPa；纵向残余应力在焊缝及热影响区表现为拉应力，并且最大值位于焊缝长度中心截面上；在圆周上表现出拉应力并伴有逐渐变小的趋势。

直缝焊管；埋弧焊；生死单元；温度场；残余应力场

直缝埋弧焊管是以热轧厚钢板做坯料，经过UO成型或JCO成型、预焊、焊接、机械扩径等工序而成的直缝埋弧焊管，质量较好，可靠性高[1-2]。焊接是直缝焊管生产中的主要工序之一，尤其对于高质量的石油天然气钢管，焊接量巨大，因此，要求的焊接质量也越来越高。然而焊接过程非常复杂，往往涉及电弧物理、传热、冶金和力学等方面。由于焊接时高度集中的瞬时热输入，导致焊后产生巨大的残余应力和变形，这些会严重影响机构件制造过程的本身以及结构的使用性能，而且残余应力的存在可能直接或间接地减少焊接构件的承载能力，特别是焊接区域高的拉伸应力往往导致脆性断裂，也可能使构件的疲劳强度降低，稳定性减小。焊接变形不仅会影响构件的尺寸公差，而且会使接头存在偏差以及增加坡口间隙，从而使制造过程更加困难[3]。

本研究利用有限元分析软件ABAQUS，并通过FORTRAN语言编写子程序DFLUX，应用“生死单元”技术，对直缝焊管纵向长直焊缝的焊接过程进行了模拟，研究直缝焊管的温度场和残余应力场的分布规律，为实际焊接生产及变形情况提供参考依据。

1 焊接物理模型的建立

1.1 温度场控制方程

在区域Ω中的热传导控制方程[4-5]为

式中：Cp—比热容；

λ—热导率；

Q—内热源强度；

T—温度；

t—时间。

温度场控制方程的热流边界条件为对流换热产生的边界上热流和辐射换热导致的边界对流。其中，对流换热产生的边界上热流计算公式为

式中：qc—热流率；

αc—对流换热系数；

T—固体表面温度；

T0C—环境参考温度。

辐射换热导致的边界对流的计算公式为

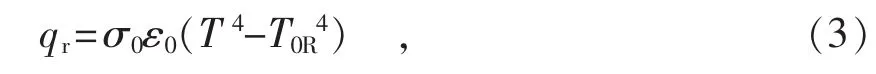
式中：qr—热流率；

ε0—黑度（发射率）；

σ0—黑体辐射常数；

T—辐射面温度；

T0R—环境参考温度。

1.2 应力场控制方程

在该区域中力平衡方程为

式中：σij,j—应力分量，已包括热应力项。

热应变的计算公式为

αij—热膨胀系数；

T0—参考温度；

δij—δ算子。

1.3 热源模型

本研究采用直缝埋弧焊焊接方法，由于熔深较深，电弧的冲击效应较大，因此，热源模型选用最接近熔池精度的双椭球热源模型[6]。

以 （0，0，0）为中心，平行于坐标轴（x，y，z），半径为a，b和c的双椭球模型的前半部分是1/4椭球，后半部分是另一1/4椭球，前后两部分椭球的能量分配系数分别为f1和f2，且f1+f2=2，其热源分布方程[7]分别为

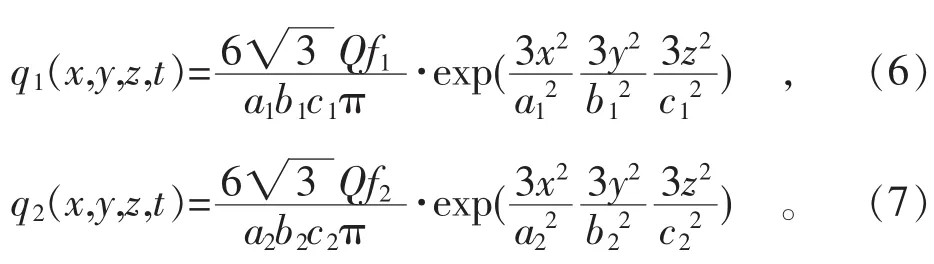
根据实际的焊接工艺参数，利用双椭球热源模型方程，计算模型上各节点的热流密度，并施加于所选节点上。电弧中心在移动过程中，重复在各节点施加热流密度，从而实现热源的移动。

2 建立有限元模型

本研究模拟的是直缝焊管的焊接过程。一般是成型预焊后，采用多丝埋弧焊对管坯的内坡口进行焊接（简称内焊），之后对外坡口进行焊接（简称外焊），工程实际中焊管外径为1 219 mm，壁厚为22 mm。

2.1 材料参数

材料的非线性热物理参量对焊接残余应力计算结果有着重要的影响[7-8]。假设焊材和母材的材料相同，具体材料参数如图1所示，图中CP为比热（×100 J/kg·℃），K为导热系数（×10 W/m·K），α为线膨胀系数（×10-5/℃），σs为屈服强度（×100 MPa），E为弹性模量（×104MPa），G为切变模量（×105MPa）。另外，在材料参数中假设不随温度变化[9]的有密度7800 kg/m3和泊松比0.3。

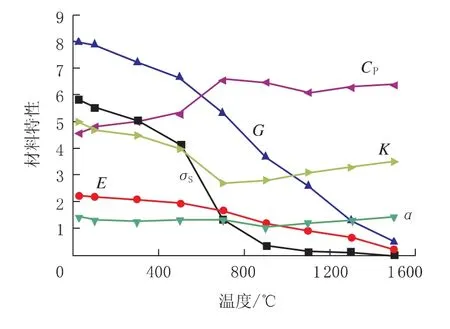
图1 材料性能参数随温度变化曲线

2.2 边界条件

温度场计算时需要给焊件表面施加对流和辐射，温度越高，辐射换热的作用越强烈。本研究将辐射换热与对流换热通过一个总的换热系数β一起考虑，边界换热损失的热能[10]表示为：qs= β(T-Ta)，其中T为温度，Ta为周围介质温度。

初始温度设定为室温25℃。应力分析时对模型施加约束，使其不存在刚性位移。

2.3 网格剖分

建立了与实际工程结构尺寸完全相同的三维有限元模型。模拟焊管规格为 φ1 219 mm× 22mm，取管长1m，并建立内外焊熔敷金属和焊管母材模型。图2为焊管接头坡口形式及尺寸。采用不均匀网格划分方法，在焊缝及其附近区域采用较细的网格，而在远离焊缝处采用较粗的网格，保证计算速度和精度。图3所示为有限元模型，共有46 750个单元，节点个数为58 395。

图2 焊管接头口形式及尺寸示意图

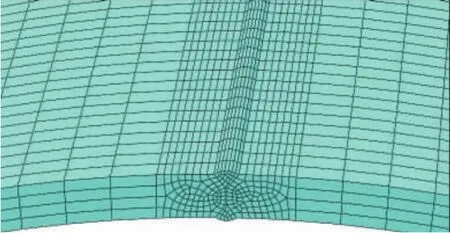
图3 有限元网格划分

2.4 焊接工艺参数

焊接采用三丝直缝埋弧焊，焊接分为内焊和外焊两部分。焊接顺序为先内焊，再外焊。焊接工艺参数见表1。

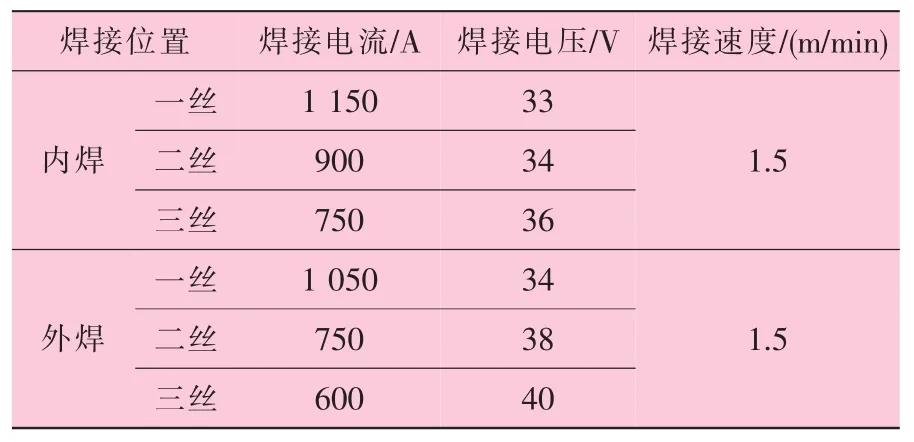
表1 焊接工艺参数

2.5 热弹塑性有限元计算

假设材料遵循热弹塑性和双线性本构模型以及Von Mises屈服准则[11-12]。在计算过程中，只考虑温度场对结构的弱耦合作用，不考虑结构对温度场的影响，即所谓 “间接耦合”的方法：先计算焊接温度场，保存每一步计算结果，再把温度场的计算结果作为体载荷施加到应力计算中。

利用“生死单元”技术[13]，描述焊接过程中焊缝从“无”到“熔化金属”，以及最终凝固的过程。即首先将内外焊缝中所有单元“杀死”，相当于焊前的装配状态。在计算过程中，再根据实际的焊接顺序，将被“杀死”的单元“激活”，从而实现模拟焊缝金属的填充过程。

在焊接阶段，通过 FORTRAN语言编写DFLUX子程序[14]，完成热源中心的移动。先将不同时刻和不同位置的热流密度值储存在已经定义好的三维表格数组中。热源的移动以步进的方式处理，当计算求解时，电弧热源从一个时间步移动到下一个时间步，求解器在自动读取下一载荷步各个节点的热流密度值的同时，会覆盖上一载荷步的热流密度值[15]。

在焊接加热阶段，设定较小的时间步长0.1s，进入冷却阶段，首先获取焊件的最高温度，然后根据最高温度值重新定义下一个步长，从而进行求解。

3 计算结果及分析

3.1 温度场计算结果及分析

图4所示是焊接时间为6.02s时的温度场分布情况，从多丝埋弧焊焊接过程中温度场的动态变化情况可知，随着焊接过程的进行，热源不断向前移动，焊件上各点的温度随时间不断变化，形成多丝共熔池，熔池附近温度较高，温度梯度大，远离热源区域，温度基本保持在25℃。

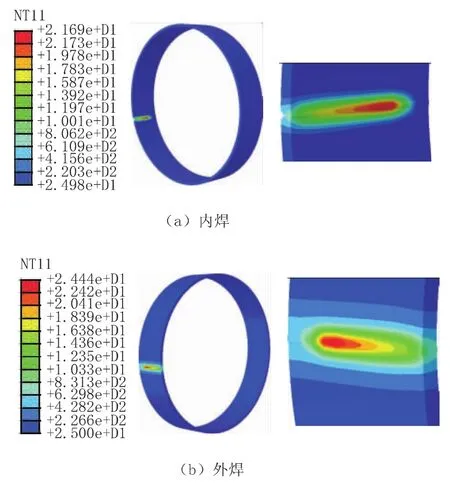
图4 焊接过程温度分布云图

内焊进行后不久，热源周围形成跟随热源同步移动的准稳态温度场，可以看出，熔池的几何形状近似为一个不规律的椭圆，其在热源移动过程中形状基本保持不变。等温线在焊接热源的前方分布密集，温度梯度大；在热源的后方等温线分布稀疏，温度梯度小。外焊时的温度分布与内焊基本一致。

提取管体外焊部位不同位置处节点的温度，绘制热循环曲线，取点位置如图5所示。其中A，B和C是焊缝中心线上轴向坐标分别为20 mm，60 mm和120 mm的点，E，F和D是B点处横截面上的点，与B点的环向距离分别是3 mm，6mm和9 mm。

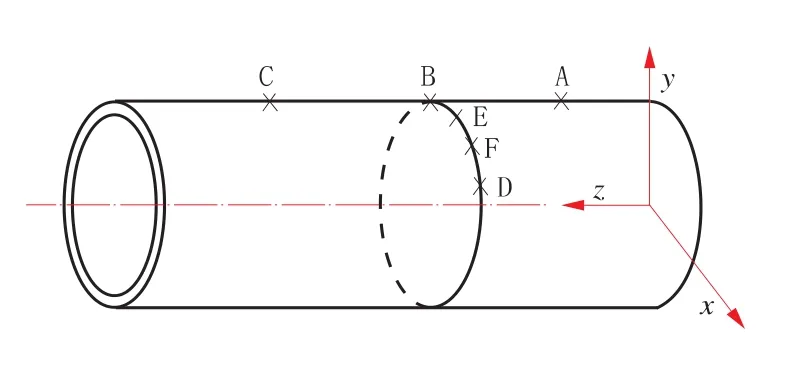
图5 采点位置示意图

图6是外焊焊接过程中B，E，F和D点的热循环曲线，反映的是温度场在管体方向的环向温度分布规律。从图6可以看出，外焊焊接过程中，焊缝附近温度梯度较大，随着距焊缝距离的增大，温度梯度逐渐变缓。离焊缝最远的地方，温度基本在600℃左右，这是由于内焊焊接时的热量传递到该处的缘故。

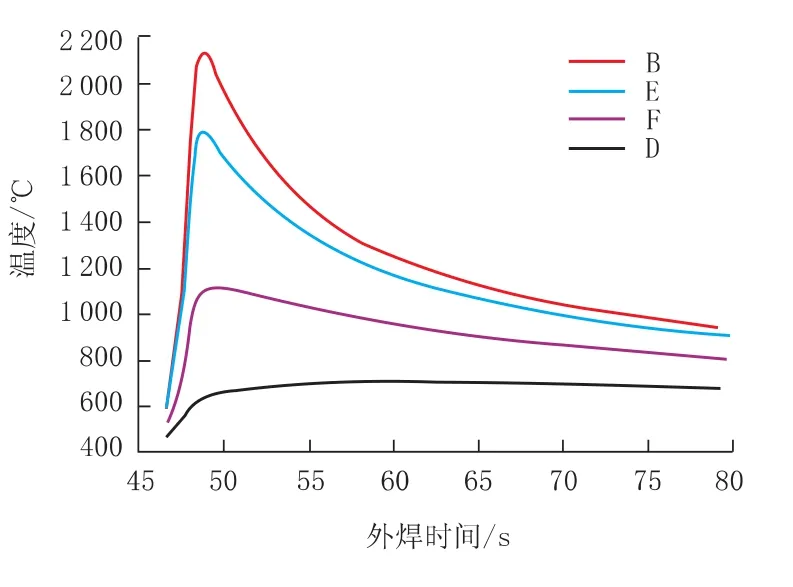
图6 B，E，F和D四点处热循环曲线

图7是A，B和C点的热循环曲线，由图7可知，热源在焊接过程中不断向前移动，焊缝上各点依次经历一个焊接热循环，当热源移动到某点时，该点温度急速上升，离开时温度快速下降，升温速率大于降温速率。

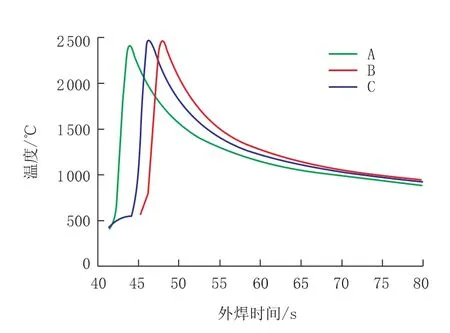
图7 A，B和C点热循环曲线

3.2 应力场计算结果及分析

图8反映了管体从内焊到外焊最后降到室温时的应力场分布情况。由图8可知，焊接残余应力始终集中分布在焊缝附近，最大残余应力也出现在焊缝处，焊接之后管体最大残余应力为528 MPa。

图8 直缝埋弧焊接后应力场分布

焊管中部进行横向切片处理时得到的应力云图如图9所示。图9反映了管体横截面上的应力分布情况，可以看出横截面的上半圆周应力较集中，残余应力相对较大，下半圆周应力普遍较小。提取该横截面外圆周上各点的残余应力值，对其进行整理，绘制相关曲线如图10所示。

图9 管体中部横截面上应力分布

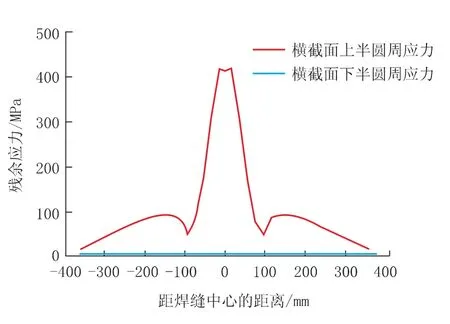
图10 焊缝中心横截面圆周上应力分布

从图10可以看出，残余应力以焊缝中心线为中心对称分布，焊缝热影响区应力较大，在焊缝所在的上半圆周面上，最大残余应力为419MPa。随着距焊缝距离的增加，残余应力逐渐减小。沿圆周方向，始终分布着残余拉应力。

从图10可以看出，整个焊缝两侧，拉应力区分布较宽，说明塑性区较宽，这与焊接时温度场的分布有关。由于焊接热输入很大，焊缝熔池较宽，电弧周围的高温区域较宽，在此区域中，热应变发展很快，加热膨胀时受到的压缩量大，随后冷却受到周围金属的拉应力，并残存下来形成残余应力。

而下半周表现出拉应力的分布规律，在焊缝中心残余应力相对较大，随着距焊缝距离的增加，残余应力逐渐减小，最大为1.93 MPa。从焊接瞬态温度场来看，下半圆由于管体直径很大，焊接温度普遍较低，温度梯度也不大，加热时所受到的压缩量较小，因此残余应力普遍较小。

在焊缝中心（管体外表面）选取一条路径，提取该路径上各点的应力值，绘制如图11所示曲线。

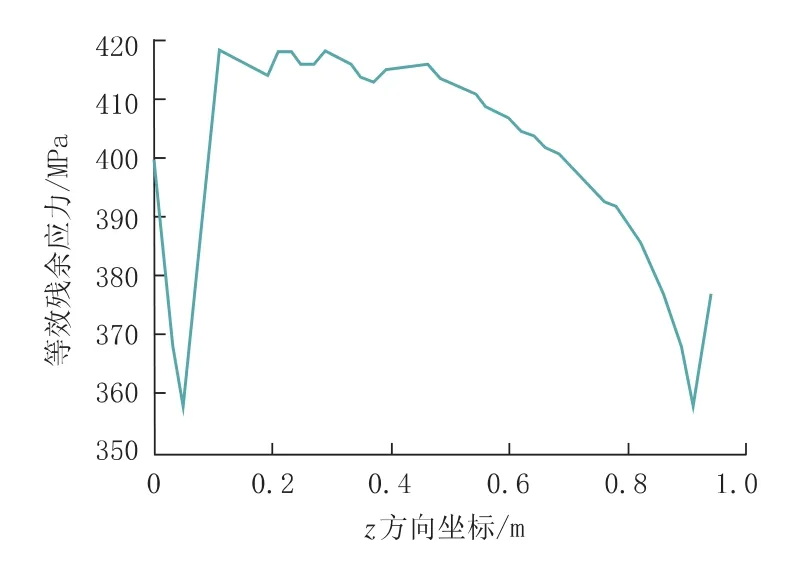
图11 沿管体长度方向的应力分布

由图11可知，沿埋弧焊直焊缝分布着残余拉应力，起焊端和止焊端的应力有些波动，不是很稳定，存在着较小的残余应力。管体中部（轴向）残余应力基本保持在413 MPa左右，残余应力存在小幅波动，这与内焊造成的残余应力有关。

4 结 论

（1）管体纵向直缝焊接温度场沿焊缝中心线呈对称分布，焊缝及其附近很窄区域内温度梯度很大，远离焊缝温度峰值急剧下降，梯度也趋于平缓，远离焊缝处大部分接近室温。

（2）内外焊接后的残余应力主要分布在焊缝及热影响区。焊缝中心残余应力值较大，管体其他部位应力很小，最大残余应力为528 MPa。在整个圆周上，表现出拉应力的分布规律，对称分布于焊缝两侧，并逐渐变小。

［1］ 宋艾玲，梁光川，王文耀.世界油气管道现状与发展趋势[J].油气储运,2006（10）:3，8-13，69.

［2］郭宝锋，金淼，任运来，等.大口径直缝焊管UOE成形技术及发展策略[J].锻压技术，2000（3）：22-25.

［3］D.拉达伊.焊接热效应温度场、残余应力、变形[M].熊第京，郑朝云，史耀武，译.北京：机械工业出版社，1997.

［4］林波，周尚荣.316L不锈钢板TIG对接焊温度场及应力场数值模拟[J].焊接技术，2009，38（4）:10-14.

［5］莫立春,钱百年.焊接热源计算模式的研究进度[J].焊接学报,2011,32(11):89-95.

［6］陈家权,肖顺湖，杨新彦，等.焊接过程数值模拟热源模型的研究进展[J].装备制造技术，2005（3):10-14.

［7］ZHU X K,CHAO Y J.Effect of temperature-dipendent material properties on welding simulation[J].Computers and Structures,2002,80(11):967-976.

［8］GOLDAK J,CHAKRAVARTI A,BIBBY M.A new finite modelforweldingheatsource[J].MetallurgualTransactions, 1984,15B（2）:299-305.

［9］ TENG T L,LIN C C.Effect of welding conditions onresidual stresses due to butt welds[J].International of Pressure Vessels and Piping,1998,75（12）:857-864.

［10］徐琳，严仁军.T形焊接接头残余应力与变形的三维数值模拟[J].江苏船舶，2007，24（1）：5-8.

［11］张玉凤，霍立兴，董俊慧.低碳钢管管道焊接残余应力有限元分析[J].焊接，2000（12）：11-15.

［12］王富耻，张朝晖.ANSYS10.0有限元分析理论及工程应用[M].北京：电子工业出版社，2006:271-272.

［13］高耀东，何雪.基于ANSYS单元生死技术的焊接模拟[J].热处理技术与装备，2010，31（1）：51-54.

［14］罗利伟，付小超.焊接残余应力的产生及其消除方法[J].山西建筑，2008，34（20）：134-135.

［15］常云龙，吴迪，佘海,等.双丝埋弧焊温度场的三维动态模拟[J].现代焊接，2012（3）:14-15.

Numerical Simulation of SAWL Pipe Welding Residual Stress

CHAO Lining1,2,BI Zongyue1,2,YU Han1,2,ZHANG Xiaofeng1,2,XIAN Linyun1,2,
ZHANG Guochao1,2,XU Kai1,2,LIANG Hang1,2
(1.Chinese National Engineering Research Center for Petroleum and Natural Gas Tubular Goods,Baoji 721008，Shaanxi,China；2.Steel Pipe Research Institute,Baoji Petroleum Steel Pipe Co.,Ltd.,Baoji 721008,Shaanxi,China)

The welding stress and deformation produced during SAWL pipe welding process affect the performance and working life of pipe.By using general finite element method(FEM)software ABAQUS,based on double-ellipsoid heat source model,to simulate the inside and outside welding process of SAWL pipe through the“birth-death element”technology,and described the distribution of quasi-steady temperature field and residual stress field on the whole pipe body.The results indicated that during welding process,the temperature gradient near weld is large;it is tend to smooth transition far away from the weld.With welding heat source moving,the temperature center also move,the highest temperature can reach the melting point of base metal.The residual stress after welding mainly distributed near weld,the residual stress in other parts of pipe is small,and the largest value of residual stress is 528 MPa.The longitudinal residual stress in weld and HAZ show tensile stress.On the circumferential direction,the longitudinal residual stress show tensile stress and accompanied by the trend of gradually smaller.

SAWL pipe;SAW;birth-death element;temperature field;residual stress field

TG404

A

1001－3938（2015）08-0024-05

中国石油天然气股份有限公司科学研究与技术开发项目“超高强度油气输送管材关键技术研究—X90/X100高压输气焊管技术研究”（项目号2012E280104）。

晁利宁（1986—），女，工学硕士，主要从事焊接成型过程的力学行为以及焊接结构断裂失效研究。

2015-01-06

修改稿收稿日期：2015-04-13

张 歌