基于未确知测度理论的岩石稳定性综合评价

宋亮华，刘　涛

（1.长沙有色冶金设计研究院有限公司，湖南长沙410011；2.西北矿冶研究院，甘肃白银730900）

基于未确知测度理论的岩石稳定性综合评价

宋亮华*1，刘涛2

（1.长沙有色冶金设计研究院有限公司，湖南长沙410011；2.西北矿冶研究院，甘肃白银730900）

岩体稳定性评价是矿山选择采掘方法和支护措施的重要依据。根据围岩的结构特征和矿山地质环境，选取了抗压强度、岩石质量指标、节理间距、节理状况、地下水状况和地应力状况6个影响因素，基于未确知测量理论，建立矿山围岩稳定性评价模型。根据矿山围岩的实测数据，建立了适合各影响因素的未确知测度函数，并对其进行定量分析，利用熵计算各影响因素的指标权重，根据置信度识别准则对岩石稳定性等级进行判定，该方法较传统的模糊数学和灰色理论等评价方法有诸多优点，该方法可对研究对象进行定量描述，更具客观性和科学性。

未确知测度理论；围岩稳定性；评价；置信度

围岩的稳定性受到很多的因素的共同影响，且各影响因素具有多变、不确定等诸多特征，从而是围岩的稳定性评价成为一个复杂的不确定性问题[1-3]。关于围岩稳定性评价的方法有很多，比如模糊数学[4]、灰色聚类[5-6]、可拓法[7-8]、人工神经网络算法[9]等，这些方法都能够较为全面地考虑各个影响因素，其评价结果与实际也较为符合。但是这些方法计算过程都较为复杂，且主观性较大。未确知测度理论是不同于模糊数学、灰色理论和随机信息等新的不确定信息，国内的一些学者将该方法引入到了边坡稳定性评价[10]、泥石流危害预测[11]、充填管道堵塞风险评价[12]等领域，并取得很好的效果，本文将该方法引入到围岩等级评价问题中，在分析影响围岩稳定性的诸多因素的基础上，通过未确知测度理论对其进行定量分析。将该方法用于甘肃小铁山铅锌矿围岩稳定性等级评价中，该方法对围岩稳定性分析和评价提供了一条新的途径。

1　未确知测度理论

将评价空间记为U，则U={C1,C2,...,Cp} 。设Ck(k=1,2,...,p)为第k级的评价等级，且k级评价危险等级要比k+1级要“高”，记为Ck＞Ck+1。如果C1＞C2＞C3＞...＞Cn，那么，{C1,C2,...,Cp} 是评价空间U的一个有序分割类。

1.1单指标测度

假设μijk=μ(xij∈ck)为测量值xij属于第k个评价等级Ck的程度，且满足以下要求：

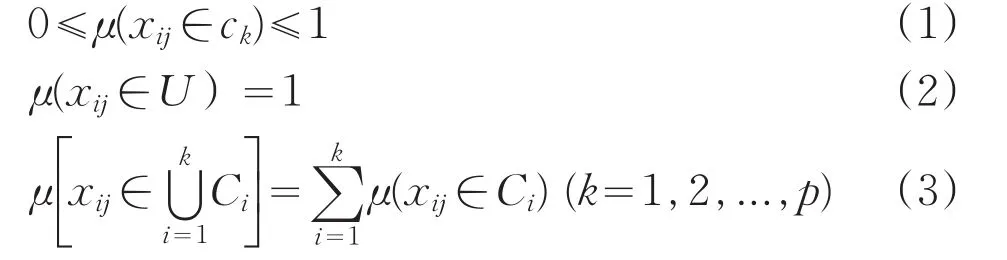
公式（2）为体现了μ的“归一性”，公式（3）则体现了μ的可加性，满足（1）～（3）的μ被称为未确定测度，简称测度。

矩阵(μijk)m×p被称为单指标测度评价矩阵，矩阵表达式为：

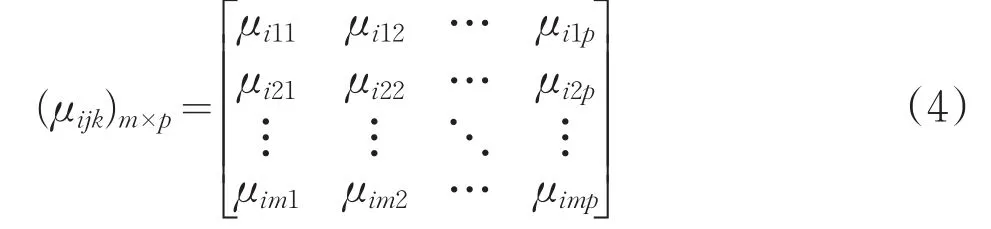
1.2指标权重的确定

假设wj表示测量指标Xj与其他的指标相对重要的程度，且，并满足，0≤wj≤1那么称wj为Xj的权重，那么向量w={ w1,w2,...,wm}被称为指标权重向量。通过熵确定指标权重，即：

通过公式（4）、（5）和（6）可算出wj。

1.3多指标综合测度

设μik=μ(Ri∈Ck)是关于评价Ri第k个评价类的程度，即有：

显然满足0≤μik≤1和=1，因此，公式（7）为μik未确知测度，{μi1,μi2,...,μip} 为Ri的多指标综合测度评价向量。

1.4置信度识别

若C1＞C2＞C3＞...＞Cp，则令：

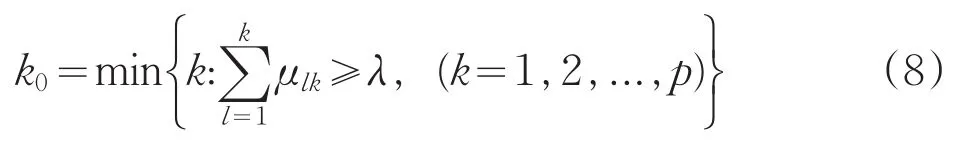
式中λ为置信度((λ≥0.5),通过引入置信度识别准则，从而对研究对象做出评价。

1.5排序

在工程当中，通常除了要对评价对象做出评价等价，往往还需对所研究的对象进行综合排序，因为通常情况下，同时处理多个危险源往往从人力和财力上对无法实现，根据危险等级和危险程度排序，可以优先处理危险程度最大的危险源，以保证在不影响生产的情况下合理、科学地降低危险源所造成的损失。若：C1＞C2＞C3＞...＞Cp，令 Cl的分值为 Il，则有：Il＞Il+1，且：

式中，Ri为R的未确知重要度，q={qR1,qR2,...,qRn}被称为评价对象未确知重要度向量。通过qRi数值的大小对其进行排序。

2　矿山围岩稳定性未确知测度评价模型

岩体由于物质组成和结构类型存在很大的差异性，其稳定性受多种因素的影响。根据以往研究和现场经验，其稳定性主要与岩石的抗压强度、岩石质量指标、节理间距、节理状况、地下水状况和地应力状况相关。因此，选取以上6个影响因素作为评价地下矿山围岩稳定性的指标体系，根据未确知测度理论，其中节理状态是指节理的宽度、连续性、表面粗糙度、节理充填物等，其最佳状态取10分，地下水根据实际情况进行量化，其中完全干燥取10分，地应力状况考虑开挖深度、剪切带、岩性及岩石膨胀性等因素，其最差状态取22分。将单个评价指标分为极稳固（C1）、稳固（C2）、一般稳固（C3）、不稳固（C4）和极不稳固（C5）5个等级，其评价指标的分级标准见表1，表1为岩体稳定性评价指标分级标准。

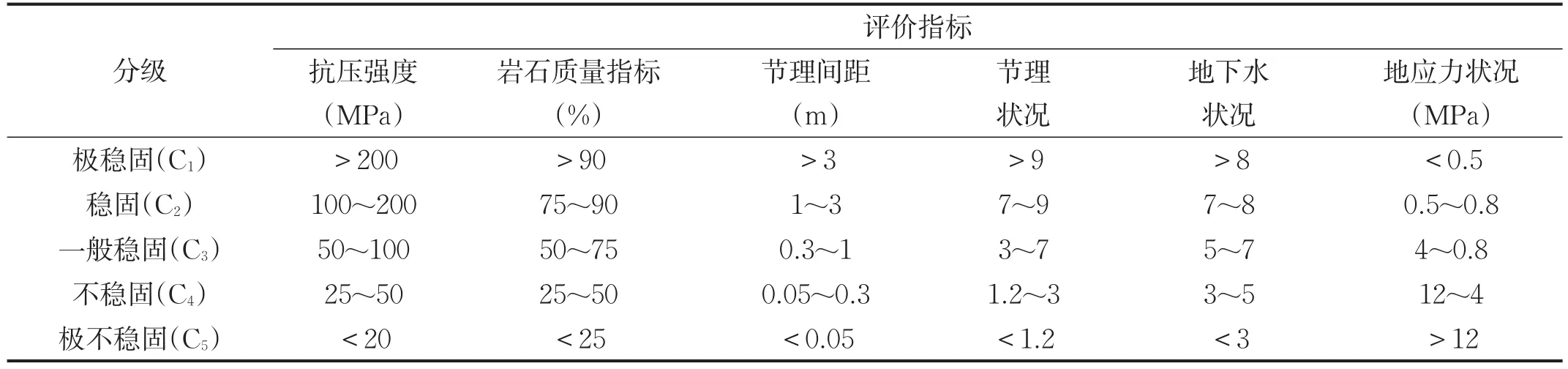
表1　岩体稳定性评价指标分级标准

根据单指标测度函数的定义及其分级标准，建立适合各指标的未确知测度函数，各项指标的测度函数如图1所示，图1为各指标的未确知测度函数。

3　工程实例

小铁山铅锌矿位于甘肃白银境内，其岩体共分为6个工程地质岩组，岩组间稳定性差别较大，故以岩组作为评价对象，该矿共有岩组6组，分别为侵入岩岩组（Mπ0）、浸染矿及矽化凝灰岩岩组（M2）、块状矿石岩组（M1）、千枚岩及片岩岩组（Mp）、绢、绿化石英角斑凝灰岩岩组（Mπ3）和破碎带岩组（F）。表2为各主要岩组稳定性评价统计数据。

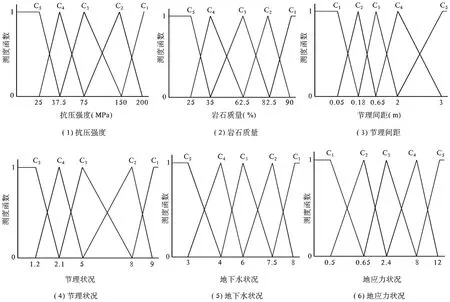
图1　单指标未确知测度函数

根据表1的分级标准和表2数据，可计算出影响各岩组稳定性的单指标评价矩阵，以侵入岩岩组（Mπ0）为例，计算可得单指标评价矩阵为：

3.1多指标评价矩阵的计算

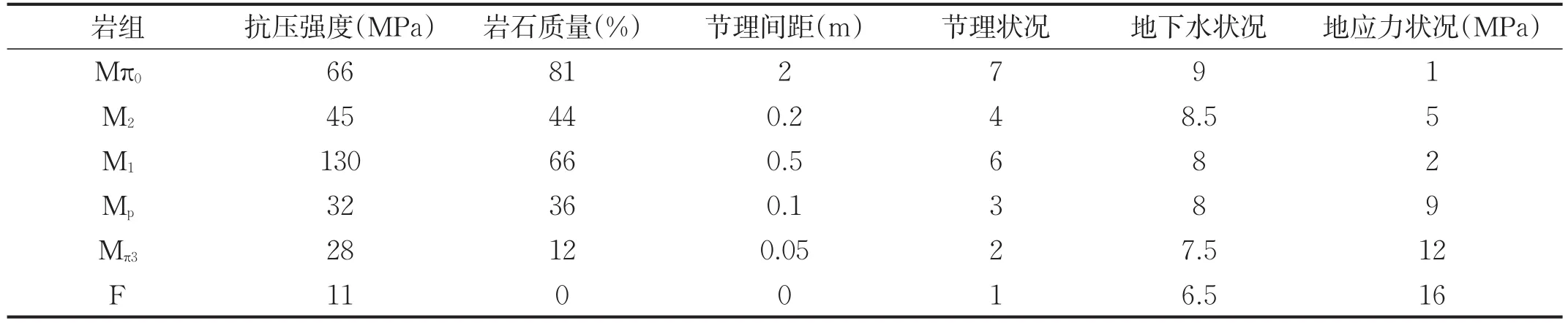
表2　各岩组稳定性评价指标

通过公式（1）～（6）可计算出各评价指标的权重，以侵入岩岩组（Mπ0）为例，计算可得可评价指标的权重为={0.13,0.17,0.22,0.12,0.22,0.14}，根据公式（7）以及单指标评价矩阵（9），可计算侵入岩岩组（Mπ0）的多指标测度评价矩阵为：{0.22,0.41, 0.33,0.04,0}，同样的计算方法，可计算出其他5个岩组的多指标测度评价矩阵，计算结果见表3。

3.2置信度识别

运用公式（8）对样本做出最后的评价结果，本文取置信度λ=0.5，以侵入岩岩组（Mπ0）为例，从大到小，k2=0.63＞0.5，从小到大，k2=0.78＞0.5，故侵入岩岩组（Mπ0）稳定性未确知测度评价结果为C2稳固，依次类推，可得出其他5个岩组的稳定性评价结果，表3为各岩组未确知测度模型的评价结果。

3.3评价结果分析

未确知测度计算的结果为Mπ0为稳固、M2一般稳固、M1一般稳固、Mp不稳固，Mπ3极不稳固和F极不稳固，为了对其评价结果进行进一步验证，将其与模糊数学评价结果和灰色聚类分析评价结果相比较，其中侵入岩岩组（Mπ0）、块状矿石岩组（M1）、千枚岩及片岩岩组（Mp）、绿化石英角斑凝灰岩岩组（Mπ3）和破碎带岩组（F）的评价结果3种方法评价一致，矽化凝灰岩岩组（M2）未确知测度与模糊数学评价结果为一般稳固，灰色聚类评价结果为不稳固，综合3种方法，综合评价结果定为C3一般稳固。

3.4稳定性排序

根据根据公式（9），对6个不同岩组进行稳定性综合排序，由于C1＞C2＞C3＞C4＞C5，假设(C1,C2,C3,C4,C5)=(5,4,3,2,1)，计 算 可 得 ：q=(q1,q2,...,q6)={3.81，3.39，3.52，2.91，1.74，1.23}，对6个岩组的稳定性从大到小进行排序：{Mπ0，M1，M2，Mp，Mπ3，F}。

在实际工程中，可针对不同稳定性的岩石组采用不同的支护方案和措施，在围岩掘井中，可根据不同岩组稳定性指数调整爆破参数和炸药单耗，减少工程成本。

4　结论

（1）运用未确知测度评价模型对小铁山矿6个主要岩组的稳定性进行了评价和等级划分，选取了抗压强度、岩石质量指标、节理间距、节理状况、地下水状况和地应力状况6个主要影响岩组稳定性的影响因素作为评价指标体系，并对其进行定量分析，利用熵计算各影响因素的指标权重，根据置信度识别准则对稳定性等级进行判定，并对其进行评价排序。

（2）将其评价结果与模糊数学和灰色聚类评价结果进行比较，其中5个岩组的稳定性评价结果一致，只有矽化凝灰岩岩组（M2）未确知测度与模糊数学评价结果为一般稳固，灰色聚类评价结果为不稳固，说明该方法的评价结果是可靠的，并且可对6个岩组的稳定性指数进行排序，模糊数学和灰色聚类评价方法则不能。

[1]曹文贵，翟友成，王江营.关口垭隧道围岩质量分级组合评价研究[J].岩石力学与工程学报，2012,31（z1）：3328-3332.

[2]董金奎，冯夏庭，张希巍，等.地下采场破碎岩体稳定性评价与参数优化[J].东北大学学报：自然科学版，2013,34（9）：1322-1326.

[3]李结全，侯福昌，潘鑫，等.岩溶区公路隧道施工围岩分级指标体系研究[J].广西大学学报：自然科学版，2013,38（1）：151-156.

[4]祁生文，伍法权.基于模糊数学的TBM施工岩体质量分级研究[J].岩石力学与工程学报，2011,30（6）：1225-1229.

[5]张庆飞，巫锡勇.灰色聚类法在围岩分级中的应用[J].西部探矿工程，2005,17（5）：112-113.

[6] 郭彬，薛希龙，徐敏.改进层次聚类法在矿山岩体分级中的应用[J].金属矿山，2011（11）：14-19.

[7] 石飞，陈忠，刘洋.巷道围岩岩体质量分级的可拓学模型及其应用[J].有色金属（矿山部分），2012,64（1）：59-62.

[8]黄生文，李森林，鲁长亮.改进的可拓方法在隧道围岩分级中的应用[J].地下空间与工程学报，2007,3（5）：878-882.

[9]宫凤强，李夕兵，高科.地下工程围岩稳定性分类的突变级数法研究[J].中南大学学报：自然科学版，2008,39（5）：1081-1086.

[10]李军霞，王常明，王钢城.基于组合赋权—未确知测度理论的滑坡危险性评价[J].岩土力学，2013（2）：468-474.

[11]刘海，陈华.基于层次分析法的未确知测度理论泥石流危险性评价[J].长江流域资源与环境，2012（8）：1032-1038.

[12] 王新民，王石，鄢德波，等.基于未确知测度理论的充填管道堵塞风险性评价[J].中国安全科学学报，2012（4）：151-156.

The Stability Comprehensive Evaluation of Surrounding Rock Based on the Unascertained Measure Theory

SONG Liang-hua1,LIU Tao2
(1.Changsha Engineering and Research Institute Ltd.Of Nonferrous Metallurgy,Changsha Hunan410011，China;2.Northwest Institute of Mining and Metallurgy,Baiying Gansu730900,China)

The stability valuation on the rock mass is the important base to select mining method and supporting measure for mines. According to the structure characteristics of surrounding rock and the geological environment in mines,the six factors of compressive strength,rock quality index,joint space,joint condition, groundwater condition and in-situ stress are selected to evaluate the rock stability.The model of surrounding rock stability evaluation in mines was established based on the unascertained measure theory.According to measured data of the mine surrounding rock the unascertained measure function suit to each factor is established.With quantitative analysis the index weight of each affecting factor is calculated by entropy,and according to the confidence recognition criteria the level of rock stability was determined.This method has many advantages compared with the traditional theory of fuzzy mathematics and grey theory,is more objective and scientific.

unascertained measure theory；surrounding rock stability；evaluation；confidence

TU45

A

1004-5716(2015)07-0001-05

2014-07-24

2014-08-21

国家重点基础研究发展计划（973）（2010CB732004）。

宋亮华（1982-），男（汉族），湖南邵阳人，工程师，现从事地质、岩土方面的研究工作。