网络条件下列车运行延误费用计算方法研究

刘先锋

LIU Xian-feng

（军事交通学院 科研部，天津 300161）

(Scientific Research Department， Military Transportation University， Tianjin 300161， China)

网络条件下列车运行延误费用计算方法研究

刘先锋

LIU Xian-feng

（军事交通学院 科研部，天津 300161）

(Scientific Research Department， Military Transportation University， Tianjin 300161， China)

在阐述国内外列车运行图稳定性研究的基础上，定义列车运行延误费用为由初始延误引发的列车晚点及停运所造成的总损失。通过构建运行图图定间隔时间矩阵、最小间隔时间矩阵得到运行图缓冲时间分布矩阵，并对网络条件下列车运行延误费用的计算方法进行设计，最后通过算例验证计算方法的通用性和可行性。

列车运行图；稳定性；延误费用；缓冲时间

0　引言

列车运行图编制质量直接决定着行车组织和运输服务的水平，其稳定性 (也称动态性能) 是列车运行图编制质量的一个重要方面，它决定了运行图在执行过程中承受随机因素扰动的能力。一般来说，列车运行图的稳定性与其实现的通过能力成反比[1]，因而在运输能力高度紧张的情况下，我国铁路运营对列车运行图的稳定性未给予足够的重视。近年来，随着铁路基础设施的改善和人们对运输质量要求的提高，行车稳定性逐渐成为我国铁路运营质量考核的主要内容。因此，评价和提高列车运行图的稳定性成为我国铁路运营所面临的重要问题。

国外对列车运行图稳定性的研究较多，提出许多运行图稳定性的评价方法和指标。Hooghiemstra A J 等[2]以荷兰铁路网为基础，运用列车运行仿真工具对列车运行延误的影响进行定量分析；Carey M[3]在对列车延误发生的类型和概率进行分析的基础上，提出一种能够在运行图编制阶段直接对列车运行图的稳定性进行评价的启发式评价方法；Tomii N[4]提出列车运行图的稳定性应根据所采取的调度措施的不同分别进行评价，将运行图稳定性分为 5 个等级，并对每个等级的评价指标进行设计；Vromans J等[5]运用仿真手段对列车的晚点传播情况进行分析，在此基础上，对运行图的稳定性与异质性的关系进行探讨；Goverde M P[6]将列车运行图看作一个离散事件系统并运用极大代数理论构建该系统的状态转移方程，以此为基础对运行图的可行性和稳定性评价方法进行研究。我国在列车运行图稳定性方面的研究相对较少，杨肇夏等[7]提出列车运行图动态性能 (即稳定性) 的概念，运用晚点传播的模拟试验对运行图的晚点传播情况进行估计，在此基础上提出一系列运行图动态性能的评价指标，并对这些指标的计算方法进行设计；孟令云[8]、陈军华[9]借鉴此研究思路对一些更为复杂的评价指标进行研究；荀径等[10]运用元胞自动机理论构建移动闭塞下列车运行的仿真模型，并运用此模型对列车晚点传播的影响因素进行分析；杨意坚等[11]在借鉴 Goverde M P 研究的基础上，提出用恢复矩阵中零元素的比例和集中程度对列车运行图的稳定性进行评价；姜雯等[12]同样运用极大代数理论对高速铁路列车运行延误模型进行研究，并通过仿真验证模型的可行性。

由此可以看出，对列车运行延误的影响进行合理预测是运行图稳定性评价的关键。但是，在网络条件下，运行图上列车间相互作用的复杂性使定量分析列车运行延误的影响的难度较大。既有研究[2,5,7,8,9,13]主要通过仿真方法实现，但这些方法普遍存在实现过程复杂、通用性差的不足。

1　列车运行延误费用定义

列车运行是由一系列的列车作业 (包括区间作业和车站作业) 组成的过程，在实际行车过程中，各项作业均有可能发生延误。当一项列车作业发生延误，会有可能影响到后续的列车作业，进而造成后续列车的晚点或停运，这一现象称为晚点传播。在这一过程中，最开始发生的列车作业延误称为初始延误，后续列车的晚点称为连带晚点。因此，通过对一项延误的影响进行测算就是对该延误引发的列车晚点及停运情况进行定量的评价。

为了对列车运行延误影响进行定量描述，定义列车运行延误费用为由初始延误引发的列车晚点及停运造成的总损失，单位为 min，计算公式为

式中：i 为列车作业编号；x 为初始延误值；k 为列车编号；m 为运行图中的列车数量；η 为 1 列车停运对旅客出行造成的不良影响，这里假定用一个较大的延误时间来表示，min；Δm 为初始延误引发的停运列车数；wk(i，x) 表示列车作业 oi发生大小为x 的延误引发的列车 traink的晚点时间；c (i，x) 表示列车作业 oi发生大小为 x 的延误所产生的总费用。

根据相关研究[4,7,12]可知，一项列车作业延误的晚点传播情况会因采用的运行调整策略不同而变化，合理的运行调整策略可以有效地抑制列车晚点的传播，降低延误的费用，因而对延误费用的计算应建立在一定运行调整策略的基础上。设定运行调整策略如下。

（1）不改变列车的运行次序，单纯通过平移运行线和增加停站来化解运行冲突。

（2）当初始延误过大以致运行冲突无法完全化解时，则删减列车运行线 (即停运部分列车) 后再运用 (1) 的方法进行调整，直到运行冲突完全化解为止。

2　运行图缓冲时间分布矩阵

运行图缓冲时间是指运行图上相邻列车作业的间隔时间中除去必要的作业时间之外富余的部分[1]。在前面设定的运行调整策略下，列车运行延误的传播主要通过运行图缓冲时间来抑制，即延误费用的大小在很大程度上是由运行图缓冲时间的分布情况决定的。因此，用矩阵来描述运行图上缓冲时间的分布情况，并以此为工具对列车运行延误的费用进行计算。

2.1定义

将网络条件下的列车运行图看作一个离散事件系统，将 1 次列车区间作业 (即列车在 1 个区间内的运行过程) 看作 1 个事件 ei，事件的开始时刻 ti就是列车驶入区间的时刻，运行图缓冲时间分布矩阵则是用以表示相邻事件间缓冲时间的矩阵。这里的相邻事件可以分为横向相邻和纵向相邻 2 类，事件 ei的横向相邻事件是指此事件所在的区间在其之后发生的第 1 个事件，纵向相邻事件则是指此事件对应的列车随后的区间运行作业所对应的事件。

对于存在 n 个事件的网络列车运行图来说，缓冲时间分布矩阵的结构为

由定义可以看出，缓冲时间分布矩阵的每一行和每一列中非 ∞ 元素的个数不超过 2 个。

给定网络列车运行图，其缓冲时间分布矩阵的构建可以分为 3 步进行：构建图定间隔时间矩阵；构建最小间隔时间矩阵；计算缓冲时间分布矩阵。

2.2构建图定间隔时间矩阵

运行图的图定间隔时间矩阵是用以表示运行图中相邻事件间隔时间的矩阵，该矩阵可由运行图中的列车运行时刻直接推算得出，具体步骤如下。

（1）初始化。列车运行图中的事件数为 n，令 i = 1。

（2）由运行图得到事件 ei的开始时间为 ti。

（3）搜索横向相邻事件。搜索 ei所在区间内(如果为双线还需是 ei所在的运行方向上) 的所有事件，得到该区间(及方向) 上事件 ei之后发生的第 1个事件 ej，进而可得图定间隔事件矩阵中的元素 ri,j为

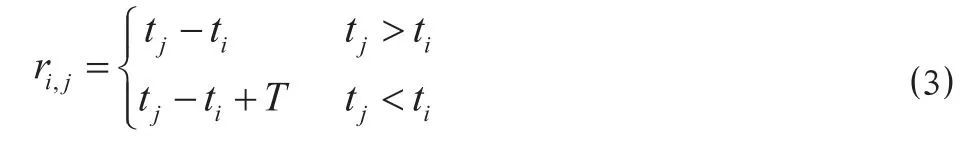
式中：T 为列车运行图的时间跨度，一般情况下，铁路行车过程均是以基本运行图为依据循环进行，即行车过程通常是以基本运行图的时间跨度 T 为周期；在这一情况下，1 个周期内某区间最后 1 个事件的横向相邻事件应为下一周期内该区间发生的第1 个事件；我国铁路运营均以 24 h 为周期，即 T = 1 440 min，因而当 tj＜ti，ri,j= tj－ti+ 1 440。

（4）搜索纵向相邻事件。搜索 ei对应列车发生的所有事件，找到其在事件 ei之后发生的第 1 个事件 ek，得图定间隔事件矩阵中的元素 ri,k为

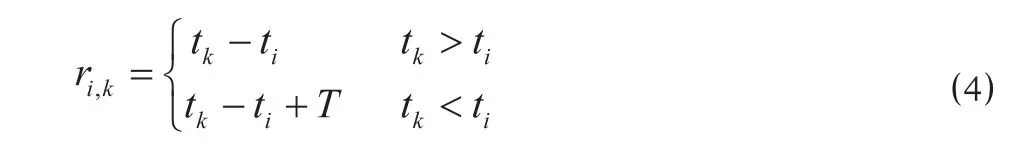
（5）若 i≠n，则令 i = i + 1 ，返回步骤 (2) ；否则，将矩阵 R 中未被赋值的元素设为 ∞，并输出矩阵 R。

2.3构建最小间隔时间矩阵

运行图的最小间隔时间矩阵是用以表示运行图中相邻事件在图定列车运行方式下所允许的最小间隔时间的矩阵。

2.3.1横向相邻事件间的最小间隔时间

在不同的线路条件 (指单双线和闭塞方式) 下，横向相邻事件间最小间隔时间的计算方法会存在一定的差异。

（1）双线自动闭塞区间内横向相邻事件间的最小间隔时间示意图如图1 所示。在双线自动闭塞区间，同方向列车可追踪运行，当前一事件的持续时间大于后一事件的持续时间 (即前一列车的运行速度小于后一列车的运行速度)，最小间隔时间等于对应区间和方向上的追踪列车间隔时间与 2 个事件持续时间的差值之和，如图1a 所示；当前一事件的持续时间小于或等于后一事件的持续时间 (即前一列车的运行速度小于或等于后一列车的运行速度)，最小间隔时间等于对应区间和方向上的追踪列车间隔时间，如图1b 所示。图1 中，ti和 tj分别为前后 2 个事件的起始时间，Δti和 Δtj分别为前后2 个事件的持续时间，ti,j为 2 个事件间的图定间隔时间，t'i,j为 2 个事件间的最小间隔时间，t缓为 2 个列车事件间的缓冲时间，I追为区间内相应方向列车运行的最小间隔时间，计算公式为

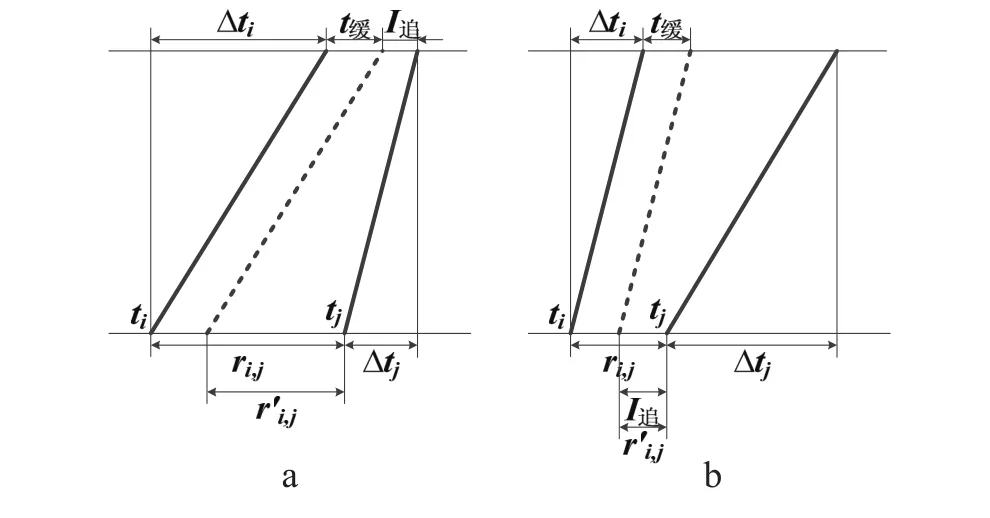
图1　双线自动闭塞区间内横向相邻事件间的最小间隔时间示意图

（2）在双线或单线半自动闭塞区间，任意时刻区间内只能运行 1 列车，而且先后运行的列车间隔必须满足进行相应车站作业的需要，半自动闭塞区间内横向相邻事件间的最小间隔时间示意图如图2所示，其中图2a 为双线半自动闭塞，图2b 为单线半自动闭塞，I站为相应的车站间隔时间。此时，最小间隔时间等于前一事件的持续时间与车站间隔时间之和，计算公式为

图2　半自动闭塞区间内横向相邻事件间的最小间隔时间示意图

2.3.2纵向相邻事件间的最小间隔时间

纵向相邻事件间最小间隔时间的计算因列车在中间车站是否进行技术作业而有所差异，纵向相邻事件的最小间隔时间示意图如图3 所示，其中图3a 为中间车站不进行技术作业，图3b 为中间车站进行技术作业，T停为列车在车站进行技术作业所需要的最小时间。

图3　纵向相邻事件最小间隔时间示意图

（1）当列车在中间车站不进行技术作业时，最小间隔时间即为前一事件的持续时间 (即列车在前一区间的运行时间)，即

（2）当列车在中间车站进行技术作业时，最小间隔时间为前一事件的持续时间 (即列车在前一区间的运行时间) 与列车在此车站的技术作业所需时间之和，即

2.3.3运行图最小间隔时间矩阵

在对相邻事件间最小间隔时间进行合理计算的基础上，按照以下过程构建运行图的最小间隔时间矩阵 R'。

（2）判断 ri,j是否为 ∞，如果不是，则进行步骤(3)；如果是，则进行步骤 (4)。

（3）计算事件 ei与事件 ej间的最小间隔时间 r'i,j。

（4）判断 j 是否为 n，如果不是，则令 j = j + 1，返回步骤 (2)；如果是，则进行步骤 (5)。

（5）判断 i 是否为 n，如果不是，则令 i = i + 1，j = 1，返回步骤 (2)；否则运算结束，输出矩阵 R'。

2.4计算缓冲时间分布矩阵

运行图缓冲时间分布矩阵等于图定间隔时间矩阵与最小间隔时间矩阵之差，即

3　列车运行延误费用计算方法

利用运行图缓冲时间分布矩阵可以对任一初始延误的费用进行计算，延误费用计算流程图如图4所示。

图4　延误费用计算流程图

3.1列车作业延误转换

由于缓冲时间分布矩阵描述的是事件间缓冲时间的分布情况，因而计算前应先将初始延误转化为相应事件的延误。①列车车站作业的延误可以看作该列车在下一个区间的运行作业对应事件发生的延误，即事件的开始时间发生相应的推迟。②列车区间作业的延误可以看作该作业对应的事件发生的延误，即事件的开始时间发生相应的推迟。

3.2事件延误时间计算子过程

给定 1 张列车运行图，其运行图事件数为 n，缓冲时间分布矩阵为运行图事件 es延误 dinitial，则图中所有事件的延误时间及停运列车数可以通过以下的过程进行计算。

（1）初始化。令 i = 0，j = 1，l = 0，Ds= dinitial， Di= 0 (i ∈ [1，n] 且 i ≠ p )，延误事件集合Δm = 0。

（3）判断 bi,j是否为 ∞，如果是，则进行步骤 (4)；如果不是，进行步骤 (5)。

（4）判断 j 是否为 n，如果是，则返回步骤 (2)；如果不是，则令 j = j + 1，返回步骤 (3)。

（5）比较 bi,j和 Di的大小，如果 bi,j≥Di，则返回步骤 (4)；如果 bi,j＜Di，则进行步骤 (6)。

（6）检验事件 ei是否已经包含在集合 ED中，如果是，则进行步骤 (7)；如果不是，则令 Dj= Di－bi,j并在集合 ED中增加 ej，返回步骤 (4)。

（7）按 ⑽ 式计算 Δm'，比较 Δm 与 Δm'，如果 Δm'＞Δm，令Δm = Δm'，返回步骤 (4)；否则，直接返回步骤 (4)。

式中：ceil (x) 为向上取整函数，M (ej) 为事件 ej对应区间上 (如果为双线还需是 ej对应方向上) 的事件数。

3.3列车晚点时间计算子过程

则列车 traink的晚点时间计算方法为

总列车晚点时间为

4　算例分析

4.1算例设定

构造一个由 6 个车站、5 个区间组成的简单路网，构造路网示意图如图5 所示，构造路网参数如

图5　构造路网示意图

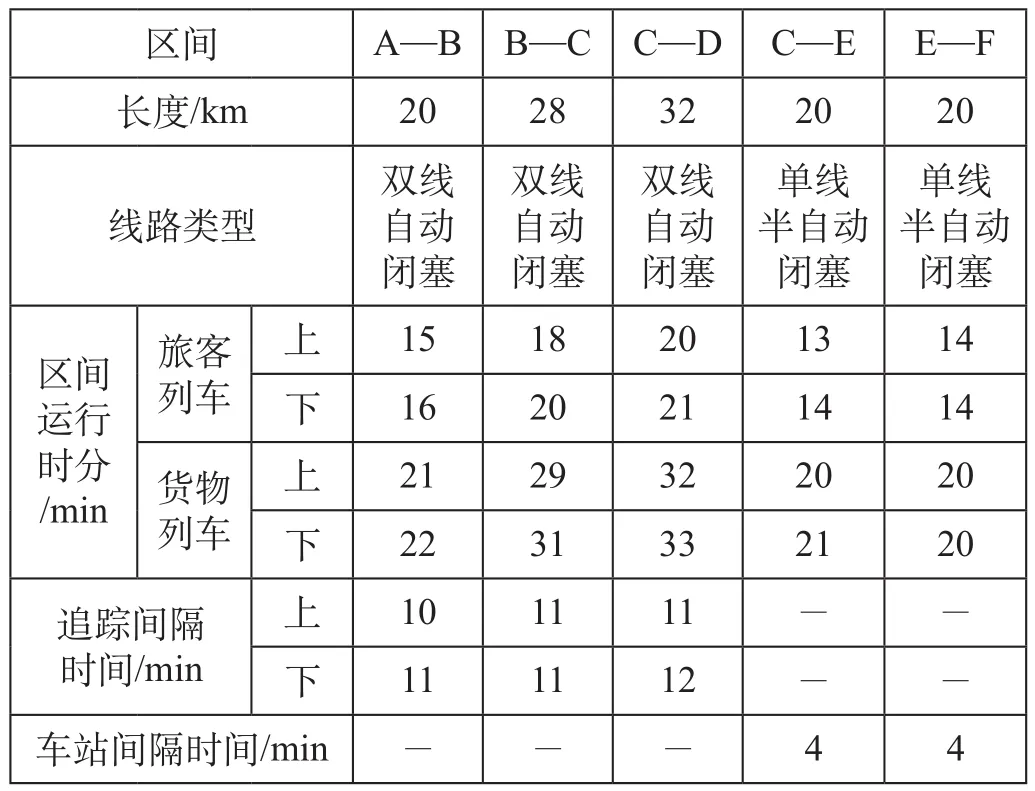
表1　构造路网参数

各站旅客乘降作业所需最小时间均为 3 min，货物列车在所有车站均不进行技术作业，并假定每停运 1 列车造成的损失为 100 min。

4.2计算结果

图6 所示的基本列车运行图共包含 84 个事件，缓冲时间分布矩阵为 84 维方阵。选取几项不同类型的列车作业，对发生不同程度的延误所产生的费用进行计算，延误费用计算结果如表2 所示。

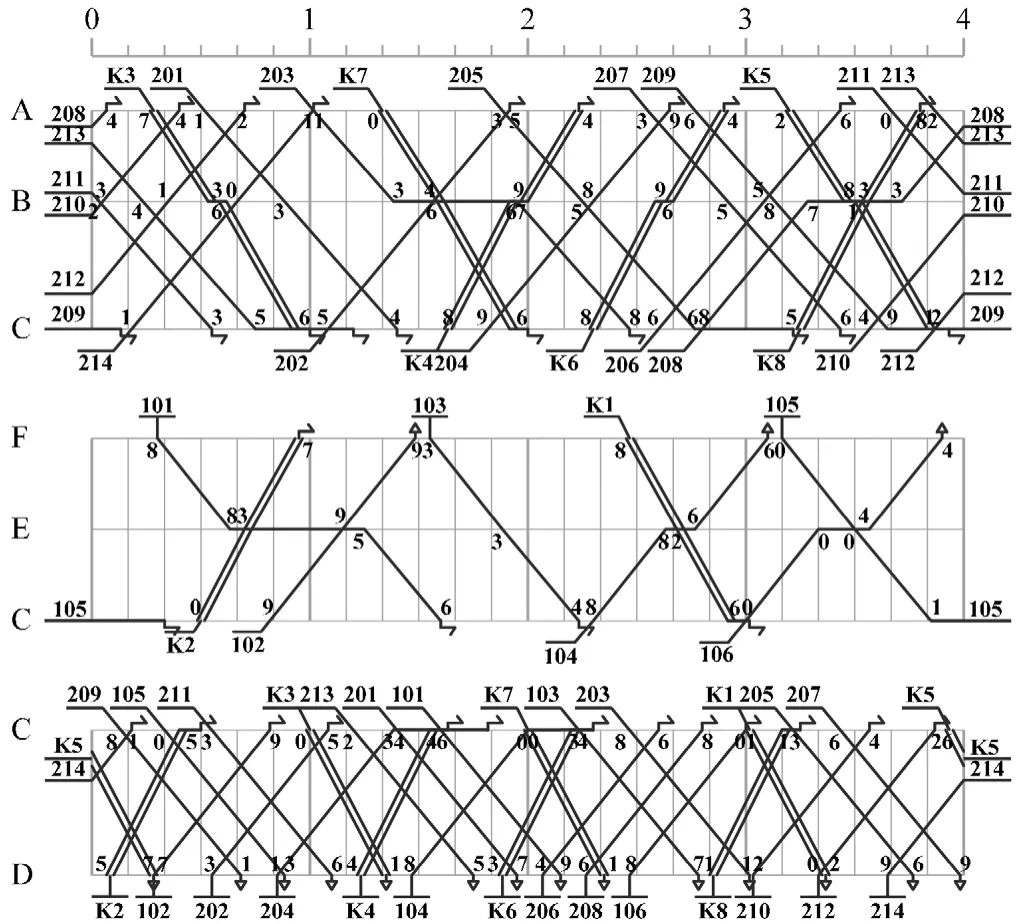
图6　构造基本列车运行图

表2　延误费用计算结果

在此基础上，进一步对这些作业发生不同大小延误时引发的费用情况进行分析，得到各列车作业延误费用变化示意图如图7 所示。由图7 可以看到，列车事件 e6和 e30处的延误所产生的费用相对较高，换言之，运行图在这 2 个位置对运行延误较为敏感；相比之下，e8和 e492 处延误影响相对较小。因此，在实际运营过程中，调度指挥人员应对K2 次列车在车站 D 处的始发作业、102 次列车在区间 C－D 间的运行过程给予更多的关注，在此位置适当增加缓冲时间或提高相应列车作业的准时性，对于保障整体运行图的实施具有更为明显的效果。

图7　各列车作业延误费用变化示意图

5　结束语

对列车运行延误的有效计算是列车运行图评价的主要内容，也是编制高稳定性运行图的基础。与传统基于仿真的计算方法相比，运用列车运行延误费用计算方法能够更为高效地实现对网络条件下列车运行延误传播的分析和计算，对于列车运行图稳定性评价和优化编制等工作效率的提升具有重要的意义，为进一步评价和提高列车运行图稳定性创造条件。

[1] International Union of Railways. UIC Code 406—Capacity [S]. Paris：International Union of Railways，2004.

[2] Hooghiemstr A J，Tunisse M. The Use of Simulation in the Planning of the Dutch Railway Services[C]//Proceedings of the 1998 Winter Simulation Conference. Washington DC：Winter Simulation Conference Board of Directors，1998：1139-1145.

[3] Carey M. Ex ante Heuristic Measures of Schedule Reliability[J]. Transportation Research Part B：Methodological，1999，33(7)：473-494.

[4] Tomii N. Robustness Indices for Train Rescheduling[C]// Proceedings of the 1st International Seminar on Railway Operations Modeling and Analysis. Delft：Delft University of Technology，2005.

[5] Vromans J，Dekker R，Kroon L. Reliability and Heterogeneity of Railway Services[J]. European Journal of Operational Research，2006，172(2)：647-665.

[6] Goverder M P. Railway Timetable Stability Analysis Using Max-plus System Theory[J]. Transportation Research Part B：Methodological，2007，41(2)：179-201.

[7] 杨肇夏，胡安洲，李 菊，等. 列车运行图动态性能及其指标体系的研究[J]. 铁道学报，1993，15(3)：46-56. YANG Zhao-xia，HU An-zhou，LI Ju，et al. A Study of the Dynamic Performance and Index System of the Train Operation Diagram[J]. Journal of the China Railway Society，1993，15(3)：46-56.

[8] 孟令云. 客运专线列车运行图动态性能及其仿真评估系统的研究[D]. 北京：北京交通大学，2009. MENG Ling-yun. Train Timetable On-line Performance and Simulation System on Railway Passenger Dedicated Line[D]. Beijing：Beijing Jiaotong University，2009.

[9] 陈军华. 基于稳定性的客运专线运行图编制与评价问题研究[D]. 北京：北京交通大学，2009. CHEN Jun-hua. Research on Establishment and Evaluation of the Stability-based Train Working Diagram of Passenger Dedicated Line[D]. Beijing：Beijing Jiaotong University，2009.

[10] 荀 径，宁 滨，李克平. 网络条件下列车追踪模型及延迟传播的研究[J]. 物理学报，2007，56(9)：5158-5164. XUN Jing，NING Bin，LI Ke-ping. Network-based Trainfollowing Model and Study of Train’s Delay Propagation[J]. Acta Physica Sinica，2007，56(9)：5158-5164.

[11] 杨意坚，何宇强. 基于 Max-plus 方法的列车运行图稳定性评价[J]. 铁道学报，2009，31(4)：14-19. YANG Yi-jian，HE Yu-qiang. Evaluation of Stability of Railway Working Diagram based on Max-plus Algebra[J]. Journal of the China Railway Society，2009，31(4)：14-19.

[12] 姜 雯，李晓娟. 基于极大代数的高速列车运行延误模型研究[J]. 铁道运输与经济，2015，37(1)：66-71. JIANG Wen，LI Xiao-juan. Study on Delay Model of Highspeed Train Operation based on Maximum Algebra[J]. Railway Transport and Economy，2015，37(1)：66-71.

[13] Salido M A，Barber F，Ingolotti L. Robustness for a Single Railway Line：Analytical and Simulation Methods[J]. Expert Systems with Applications，2012，39(18)：11305-11327.

责任编辑：刘 新

Study on Algorithm for Calculating Train Operation Delay Cost under Network

Based on expounding the stability study on train working diagram in China and foreign countries, this paper defines the train operation delay cost as the total losses caused by train delay and cancellation which arises from initial delay. Through building interval matrix and minimum interval matrix of train working diagram, the distribution matrix of buffer time of the diagram was established, and the algorithm for calculating train operation delay cost under network was put forward. In the end, the universality and feasibility of the algorithm was validated through calculation example.

Train Working Diagram; Stability; Delay Cost; Buffer Time

1003-1421(2015)11-0015-07+1

A

U292.4

10.16668/j.cnki.issn.1003-1421.2015.11.04

2015-09-21