潜艇水下回转运动数学模型研究与仿真分析

陈志法，戴余良，邓 峰，倪 刚

(1.海军工程大学 动力工程学院，湖北 武汉430033;2.中国人民解放军92351 部队，海南 三亚527000)

0 引 言

近些年各国陆续提出了发展海洋经济、维护海洋权益的战略方向，海军的地位日益提高，潜艇作为现代海军的威慑力量之一，其作用也愈显重要。为了捕捉战机、占据有利位置，或者是快速撒离战场、有效规避反潜武器的攻击，潜艇水下回转运动成为一种常用的运动方式，它是潜艇定深直航、变深潜浮和转向机动等3 种最重要、最基本的运动方式之一［1］，因此有必要对其进行研究。潜艇水下回转运动时，艇体受力受横向流影响极大，把潜艇看成一个刚体，利用潜艇重心处的运动参数对其进行求解的传统方法不再适用，所以本文通过分析对比不同的运动方程，得出合理有效的潜艇水下回转运动数学模型，采用分段计算方法对潜艇水下回转运动横向水动力进行建模仿真，重点分析了潜艇水下定常回转运动时漂角、回转角速度、横倾角以及纵倾角的变化规律，为下一步研究潜艇水下回转运动非线性特征打下基础。

1 潜艇水下回转运动数学模型

研究潜艇水下回转运动规律，模型是基础。目前，世界上对潜艇运动模型的研究有很多，1967 年美国泰勒海军舰船研究与发展中心(DTNSRDC)在进行大量船模试验和实艇试航的基础上，发表了“用于潜艇模拟研究的标准运动方程”［2］(本文称其为67 方程)，因其具有较高权威性而被国际拖曳水池会议(ITTC)所采纳，并为广大研究人员所引用［3］。运用67 方程对潜艇进行研究时，人们把潜艇看成一个刚体，利用潜艇重心处的运动参数对其进行求解，其中海军工程大学的林俊兴等人于2014 年利用此方程对潜艇定常回转运动的参数变化规律进行了研究［4］。然而1975 年Feldman，J. 在对计算机模拟预报与实艇试验结果的相关性分析中指出，67方程及其相应的系数在大多数情况下可以对潜艇水下前进运动轨迹做出精确的预报，预报结果与实艇试验吻合良好，重复性也很好。但是在强机动情况下，如高速、大舵角回转运动等，其对深度改变、纵倾角和横倾角的预报需要进一步改进［1］。究其原因，主要是由于潜艇细长型的结构特点，在做高速、大舵角回转运动等强机动时，潜艇沿艇长方向各点的受力受横向流影响极大，潜艇运动非线性现象突出。所以，67 方程不能精确地对潜艇水下回转运动进行模拟仿真。DTNSRDC 于1979 年在67 方程的基础上又发表了“修正的潜艇标准运动方程”［5］(本文称其为79 方程)，相比于67 方程，79 方程更多考虑了螺旋桨负荷和航速变化的影响、高速大舵角回转运动中横向流突出的问题以及水动力产生的历程效应，同时它也调整了部分水动力项，使其在理论上能精确地适用于各种复杂环境下潜艇运动轨迹的预报，并且可以准确运用于潜艇运动非线性研究［1］。79 方程对67 方程有很多改进之处［6］，本文结合具体研究工况，分析潜艇水下回转运动的受力情况发现，横向水动力是影响回转运动的主要因素，因此重点分析79 方程与67 方程中横向力表达式的区别，结果表明，79 方程对部分受横向流影响的横向水动力项进行修正，引入横向流阻力系数Cd，将其从非积分形式改为积分形式，如表1 所示。

表1 横向力方程水动力项的变化Tab.1 The variation of the hydrodynamic item in the yawing force equation

其中:h(x)是艇体在xoz 平面内、艇长x 处的局部的高度，v(x)=v +xr 和w(x)=w -xl 分别为此点在z，y 方向的速度分量。

本文采用的潜艇运动方程以79 方程为基础，针对水下回转运动工况，参照文献［7 -8］所述模型，充分考虑潜艇水下回转运动时横向流的影响，同时省略影响较小的项，得到具体表达形式如下:

1)轴向力方程

横向力方程:

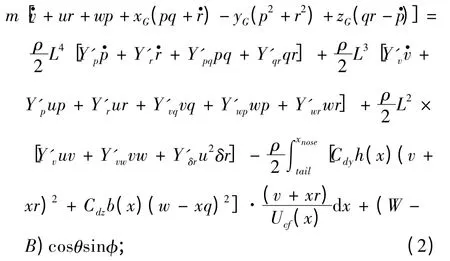
2)垂向力方程

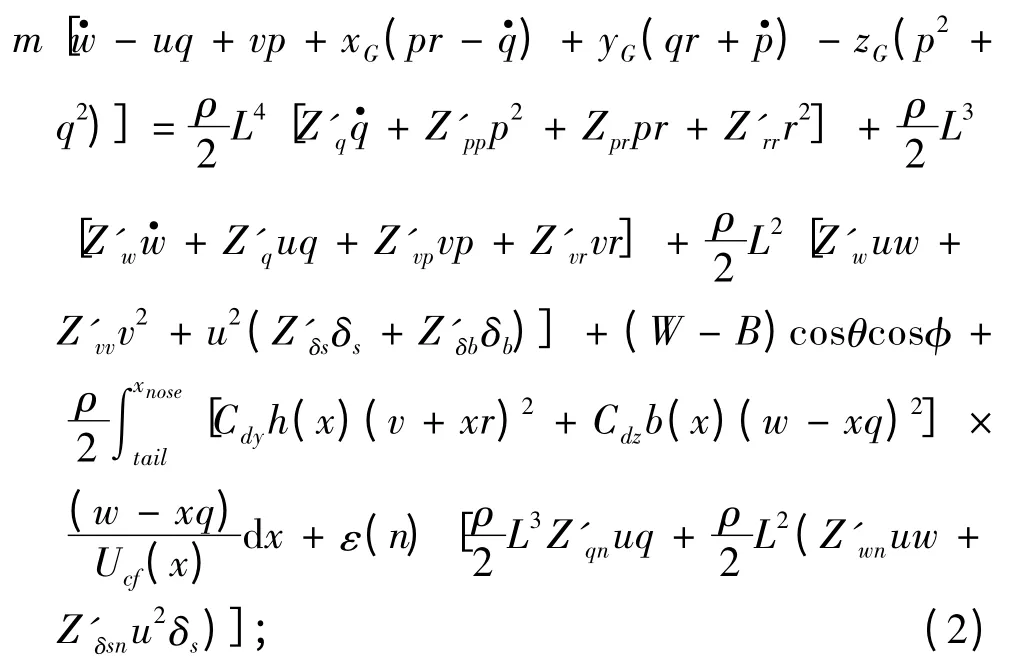
3)横摇力矩方程

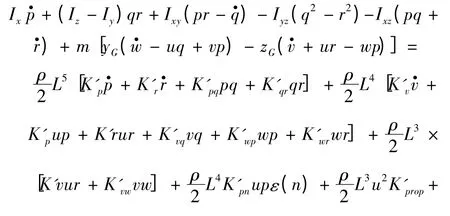
4)纵倾力矩方程

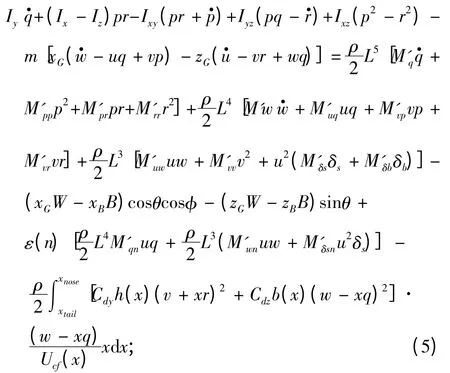
5)偏航力矩方程

6)运动关系式

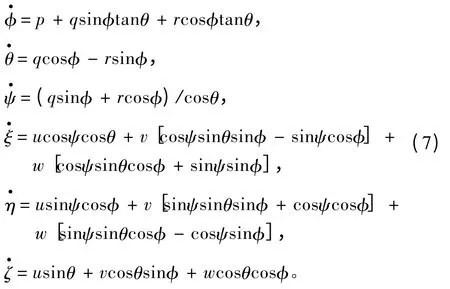
式中:运动坐标系(简称动系)O-xyz 固联于潜艇艇体上;u，v，w 分别为纵向速度、横向速度、垂向速度;p，q，r 分别为横倾角速度、纵倾角速度、偏航角速度;φ，θ，Ψ 分别为横倾角、纵倾角、航向角;W 为潜艇重力;B 为潜艇浮力;δr，δb，δs分别为方向舵舵角、首升降舵舵角、尾升降舵舵角;xG，yG，zG为重心坐标;xB，yB，zB为浮心坐标;n 为螺旋桨转速;其他参数意义参照文献［2］和文献［5］;右上角带“′”的项为水动力系数项，其值及其他参数值大小参考文献［7］。

2 潜艇水下回转运动仿真

2.1 Matlab 建模

上述数学模型中使用了积分表达式，这给实际工程应用带来不便。由积分学的原理可知，积分是将物体分成无限段再求和，而在实际工程运用当中不可能进行无限分段，只能进行有限分段再求和，分段越多，积分精度越高，但计算越复杂;而分段越少，计算越简单，但不利于积分精度。所以本文借鉴积分学的思想，采用一种沿x 轴各点分布的近似计算方法——分段计算方法，对潜艇水下回转运动横向水动力进行计算，即将潜艇沿艇长方向平均分成若干段，以每段中心点的横向水动力作为整段的平均横向水动力，计算各段的受力情况，再将各段的力进行矢量相加，求出整艇的横向水动力。为了减少计算量，同时又保证足够的计算精度，找到一个合理的分段数是必要的。针对本文的研究对象，经分析研究认为将潜艇沿艇长方向等分为10 段来近似计算艇体的受力情况已经足够简便和准确，故将潜艇沿艇长方向等分为10 段，并用Matlab 软件进行建模。

2.2 运动参数仿真

潜艇水下回转可根据运动过程中参数的变化特点将其分为转舵阶段、过渡阶段和定常阶段［1］，本文研究的是潜艇水下回转运动进入定常阶段时漂角βs、回转角速度rs、横倾角Φs以及纵倾角θs随方向舵舵角δr和航速U 的变化规律。设定在无限深、广、静的流场中，以上述Matlab 仿真模型为基础，分别设定仿真航速U 为4 kn，8 kn，12 kn，16 kn，19 kn，21 kn，22 kn;分别操5°，9°，12°，14°和15°方向舵，仿真计算结果如表2 所示。

2.3 仿真结果分析

分析表2 可知，潜艇水下定常回转运动时:

1)漂角随着方向舵舵角的增大而增大，但随航速的变化不大。由此可知，漂角的大小主要受方向舵舵角的影响而与航速关系不大。潜艇小舵角回转时，漂角随舵角线性增长，但大舵角运动时(如大于12°)，增长趋势呈非线性化，如图1 所示。

2)回转角速度分别随着方向舵舵角和航速的增大而增大。

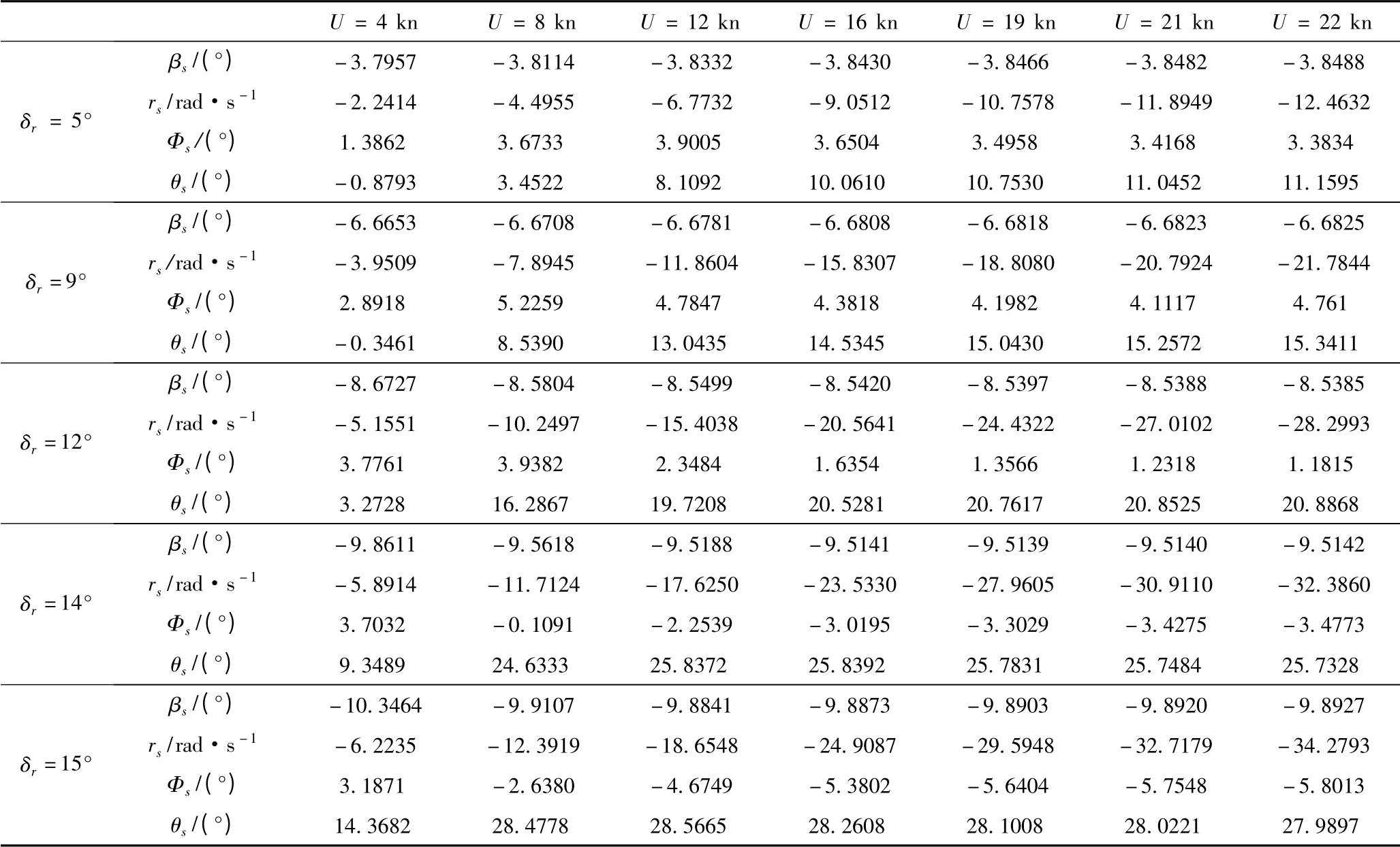
表2 潜艇水下定常回转运动参数Tab.2 The parameters of submarine in steady rotary movement under water

①航速不变时，随着方向舵舵角的增大，横倾角先增大后快速减小，潜艇由内倾变为外倾，如图2 所示，小舵角时，使潜艇内倾的艇体横向力对潜艇横倾起主要贡献作用，潜艇内倾，随着舵角的增大，漂角增大，但艇体横向水动力增大的速度大于方向舵舵力的增大速度，内倾角继续增大。当舵角增大到某一值后，随着舵角的增大，艇体横向力增大的速度小于方向舵舵力的增大速度，最终艇体横向水动力小于方向舵舵力的横向分量，于是艇体横倾角出现先增大后快速减小、由内倾变为外倾的现象。

②方向舵舵角一定时，可分以下2 种情况(见图3):一是小舵角(如小于12°)回转时，横倾角随着航速的增大先增大后缓慢减小。这主要是因为潜艇小舵角回转时，使潜艇内倾的艇体横向力对潜艇横倾起主要贡献作用，随着航速的增大，艇体横向力增大，横倾角也相应增大，但是，与此同时，使潜艇外倾的舵横向分力也逐渐增大，且幅度大于艇体横向力增长的幅度。所以横倾角随着航速的增大呈先增大后缓慢减小的变化趋势。二是大舵角回转时，艇体随着航速的增大逐渐由内倾变为外倾。这是因为低航速回转时，艇体横向力大于舵横向分力，所以艇体呈内倾姿态，之后随着航速的增大，舵横向分力迅速增大，直到大于艇体横向力，潜艇由内倾变为外倾。

3)小舵角、低航速的情况下潜艇呈首倾状，即纵倾角小于0，此时若保持航速不变，方向舵舵角逐渐增大，则纵倾角将由首倾变为尾倾，并逐渐增大，如图4 所示;若保持方向舵舵角不变，航速增大，则纵倾角逐渐增大同时增大幅度放缓，直至基本保持最大值不变，如图5 所示。

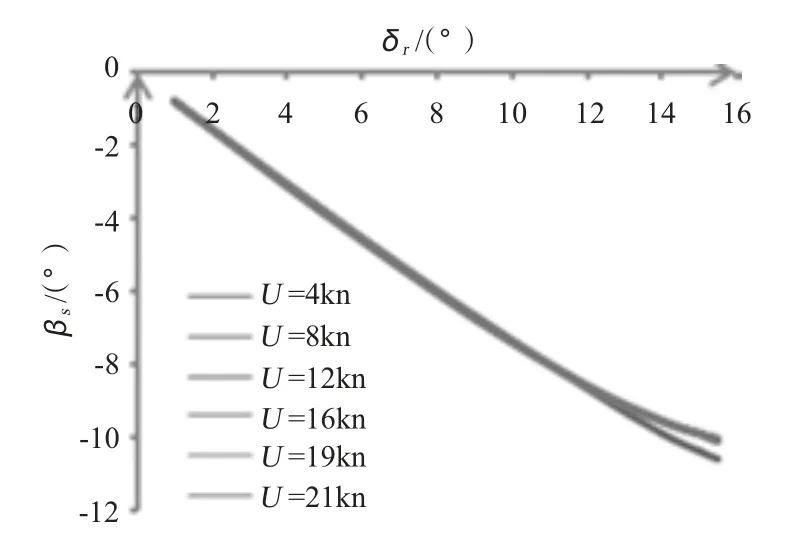
图1 βs 随δr 的变化情况Fig.1 βs versus δr

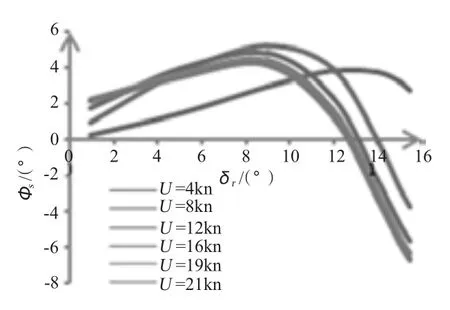
图2 Φs 随δr 的变化情况Fig.2 Φs versus δr

图3 Φs 随U 的变化情况Fig.3 Φs versus U

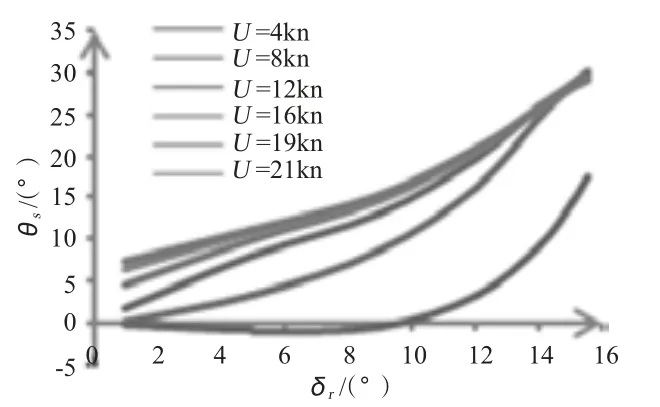
图4 θs 随δr 的变化情况Fig.4 θs versus δr

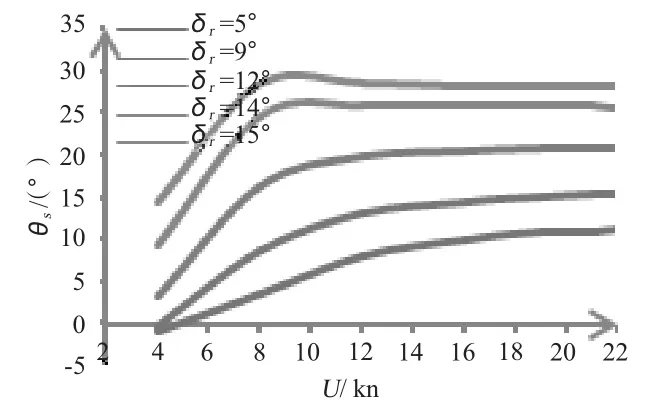
图5 θs 随U 的变化情况Fig.5 θsversus U

由上述分析可知，仿真结果与理论分析和实艇操纵规律基本一致，从而说明本文所用潜艇数学模型和建模仿真方法正确有效。潜艇水下回转运动进入定常阶段时，艇体以一定的角速度作等速圆周运动，同时存在明显的横倾、纵倾等耦合运动现象，这与潜艇回转运动时存有较大的非线性成分有关。尤其当潜艇高速大舵角回转时，横向流突出，艇体上所受流体动力和力矩的大小与航速、漂角以及回转角速度等因素密切相关，此时潜艇运动参数超出了常规的线形范围，不能用线性方程进行求解［1］。从式(2)亦知，潜艇横向受力方程中存在众多高次项、耦合项等非线性项，所以有必要进一步开展潜艇水下回转运动非线性分析。

3 结 语

本文对67 方程和79 方程进行对比分析，得出了合理有效的潜艇水下回转运动数学模型，借鉴积分理论的思想，采用分段计算方法对潜艇水下回转运动横向水动力进行建模仿真，重点分析了潜艇水下定常回转运动时参数的变化规律，其结果与实艇操纵规律基本一致，从而说明本文所用潜艇数学模型和建模仿真方法是正确有效的。研究表明，潜艇水下回转运动时存在明显的横倾、纵倾等耦合运动现象，潜艇横向受力方程中存在众多高次项、耦合项等非线性项，艇体运动参数超出了常规的线形范围，不能用线性方程进行求解，所以下一步有必要开展潜艇水下回转运动非线性研究。

［1］施生达.潜艇操纵性［M］.北京:国防工业出版社，1995.SHI Sheng-da. Submarine maneuverability［M］. Beijing:Notional Defence Industry Press，1995.

［2］MORTON G，GRENT R H.Standard equations of motion for submarine simulation［R］.AD-653，861，SNAME，1967.

［3］林雄伟，胡大斌，戴余良. 潜艇非线性运动研究综述［J］.船舶力学，2013，17(1 -2):187 -195.LIN Xiong-wei，HU Da-bin，DAI Yu-liang. Overview on the research of submarine nonlinear motion［J］. Journal of Ship Mechanics，2013，17(1 -2):187 -195.

［4］林俊兴，倪刚，戴余良，等.潜艇定常回转运动参数变化规律研究［J］.舰船科学技术，2014，36(1):31 -37.LIN Jun-xing，NI Gang，DAI Yu-liang，et al.Research on parameters′change rule of submarine′s steady rotary movement［J］.Ship Science and Technology，2014，36(1):31-37.

［5］FELDMAN J.DTNSRDC revised standard submarine equations of motion［R］.DTNSRDC Report SPD，1979:393-09.

［6］倪刚，林俊兴，唐成，等.修正的潜艇标准运动方程的应用［J］.舰船科学技术，2013，35(11):41 -44.NI Gang，LIN Jun-xing，TANG Cheng，et al.Applied study of submarine′s standard movement equation of the revise［J］.Ship Science and Technology，2013，35(11):41-44.

［7］HEALEY A J，LIENARD D. Multivariable sliding mode control for autonomous diving and steering of unmanned underwater vehicles ［J］. IEEE Journal of Ocean Engineering，1993，18(3):327 -339.

［8］BONCAL R J.A study of model based maneuvering controls for autonomous underwater vehicles［D］. California:Naval Postgraduate School，1987.