宽扁型环肋骨圆柱壳强度和稳定性分析
2015-12-20黄加强
黄加强,陈 杰
(1.海军驻武汉第七一九研究所军事代表室,湖北 武汉430064;2.武汉市第二船舶设计研究所,湖北 武汉430064)
0 引 言
加筋圆柱壳作为深潜器的主要耐压结构,在工程上有着广泛应用。加筋圆柱壳结构的强度和稳定性一直以来被众多学者和设计者所关注,也出现了诸多研究成果[1-3]。
传统水下结构物普遍采用T 型材和球扁钢等肋骨形式。朱邦俊等[4]对半圆环壳耐压圆柱壳强度和稳定性进行分析研究,推导了相应的计算公式,并采用实验方法进行验证;吕春雷等[5]采用理论分析和数值计算方法对不同型式加筋的圆柱壳稳定性进行对比分析,并给出了关于加强筋设计的建议。为了提高圆柱壳的屈曲承载能力,龙连春等[6]对加筋圆柱壳结构进行优化设计分析,得到了加筋圆柱壳合理的布筋方案。
目前研究的环肋骨结构截面宽度与高度的比值普遍都小于1,但是对于有些深潜器而言,需要对诸多设备进行布置和安装,由于受到其内部空间的限制,在设计其耐压结构时,其内部加强筋高度不宜设计过高。为了增加肋骨刚度,只有通过增加肋骨宽度的方式实现,这样就产生了一类特殊的耐压结构形式——宽扁型环肋骨加筋圆柱壳,如图1 所示。本文针对这种特殊的结构形式,采用Ansys 软件对其强度和稳定性进行计算分析,对比了2 种建模方式下计算结果的差异性,并且与规范值进行比较。同时,通过有限元计算,分析加筋尺寸以及加筋布置方案对结构极限承载能力的影响。
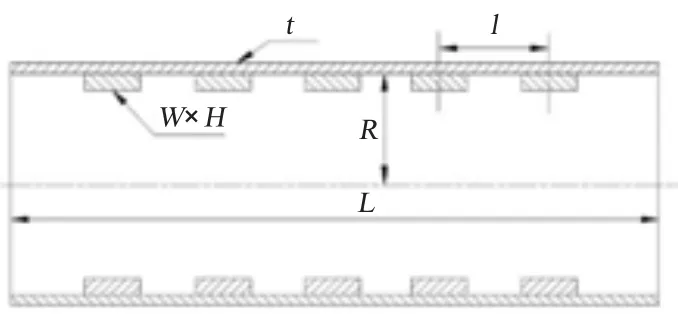
图1 宽扁型环肋骨加筋圆柱壳结构剖面图Fig.1 Cross-sectional view ofring-stiffened cylindrical shell withflatribs
1 宽扁型肋骨加筋圆柱壳强度有限元分析
内加筋圆柱壳几何模型如图2 所示。耐压圆柱壳半径R = 190 mm,耐压壳板厚t = 7 mm,肋骨间距l = 220 mm,宽扁梁截面尺寸为40 ×18 mm。材料为铝合金,弹性模量E = 6.9 ×104MPa,泊松比μ =0.32,屈服强度σs= 380 MPa,工作压强P = 4 MPa。

图2 典型宽扁梁加筋圆柱壳几何模型Fig.2 Typical geometry of stiffened cylindrical shellwith flat ribs
采用有限元通用软件Ansys 进行有限元建模分析。传统的加筋圆柱壳一般采用壳单元和梁单元进行模拟,由于宽扁型环肋骨加筋圆柱壳具有一定的特殊性,本文将采用2 种不同方法进行模拟计算:1)全部采用体单元;2)圆柱壳采用壳单元,加强筋采用梁单元。将这2 种模拟方法的计算结果进行对比分析,同时与规范计算值进行比较。
1.1 宽扁型环肋骨加筋圆柱壳强度有限元计算
Ansys 软件中体建模采用solid45 单元模拟;壳、梁单元建模中壳采用shell63 单元,梁采用beam188单元。网格大小保证两者在周向份数和每个肋距内份数相同。
规范校核中3 个典型位置处的应力分布云图如图3 ~图5 所示。

图3 相邻肋骨跨中壳板中面周向应力分布云图Fig.3 Circumferential stress contours of the middle layer between adjacent ribs

图4 肋骨跨端壳板内表面纵向应力分布云图Fig.4 Longitudinal stress contours of bottom layer on cross ribs

图5 肋骨应力分布云图Fig.5 Stress contours of the rib
由图3 可知,壳板在跨中处取得最大周向应力,应力分布规律一致。图4(a)显示了体单元内外表面的纵向应力,而图4(b)显示为壳单元内表面纵向应力,都表现为肋骨跨端处内表面应力最大,但是体单元最大应力出现在肋骨与壳板截面突变处,而壳单元出现在肋骨中心线处。图5 显示两者应力分布差异很大,体单元肋骨沿厚度方向有应力梯度,而梁单元肋骨为同一应力值。
1.2 宽扁环肋骨加强圆柱壳强度有限元计算与规范计算对比分析
有限元计算值与规范计算值如表1 所示。
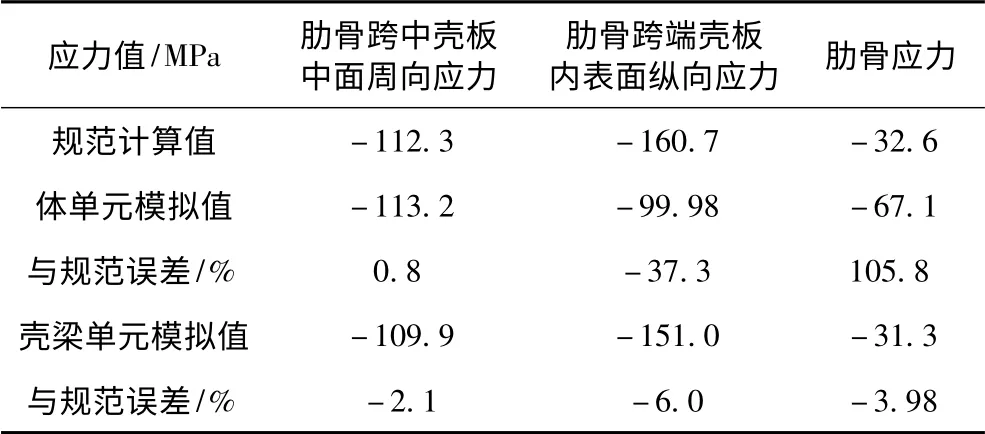
表1 有限元计算与规范计算对比Tab.1 Comparison of calculation between finite element and norm
除肋骨跨中壳板中面周向应力误差较小外,体单元模拟计算值与规范计算值的差异较大;而壳、梁单元模拟计算值与规范计算值误差在6%以内,能很好的与规范吻合。
体单元模拟肋骨与壳板共面连接,使得肋骨跨端纵向应力出现在板厚突变处,而不再是肋骨中心线处,这与梁、壳单元模拟有所不同。体单元建模能更准确的反映宽扁梁加强圆柱壳的应力分布。通过对比分析,对于这种特殊的宽扁环肋骨形式,规范中的强度校核部分不再适用。
2 宽扁型肋骨圆柱壳稳定性分析
随着下潜深度增加,耐压圆柱壳结构在静水压力的作用下会出现屈曲失稳。由于耐压结构的失稳往往发生在材料的非线性阶段[7],因此,关于肋骨加强耐压圆柱壳稳定性计算,需要同时考虑壳体的几何非线性(如初始缺陷)和材料非线性的影响。
2.1 宽扁环肋骨加强耐压圆柱壳稳定性有限元分析
本文采用双线性材料模型,初始缺陷幅值取耐压圆柱壳半径的0.25%。Ansys 软件中线性屈曲与非线性屈曲的区别在于材料属性的定义,非线性屈曲需要定义材料屈服强度和材料切线模量(取弹性范围内杨氏模量1%);施加单位载荷以得到结构特征值屈曲模态,再将屈曲模态以给定的幅值施加到原结构中生成新的有限元模型,形成了以特征值屈曲模态为初始缺陷的非线性屈曲有限元计算模型。
宽扁环肋骨加强圆柱壳的特征值屈曲失稳波形如图6 所示,图示为第一阶失稳波形(整体失稳)。图7 和图8 分别为破坏载荷下的位移分布云图和位移—载荷曲线图。

图6 整体失稳波形Fig.6 Buckling mode

图7 破坏载荷下位移云图Fig.7 Shell deformation contourwhen collapsed

图8 典型位置处位移—载荷曲线Fig.8 Load-displacement curve of theshell
规范中计算结构整体失稳临界压力时,考虑了结构的几何修正和物理修正。有限元计算值与规范计算值见表2。

表2 整体失稳临界压力有限元值与规范值对比Tab.2 Comparison of overall instability pressure between finite element and norm
体单元整体失稳临界压力较规范计算值偏大,与规范值误差为22.4%左右,有较大差异。对于本文中的特殊肋骨形式规范中稳定性校核部分不再适用。
3 加筋尺寸及布置方案对结构极限承载能力影响分析
3.1 加筋尺寸对环肋加筋圆柱壳极限承载能力影响分析
对于某些深潜器,由于其内部空间有限,为满足内部设备安装等要求,加强筋高度方向的尺寸可能受到限制不能加大,为了提高其极限承载能力,只有增大加强筋的宽度。本节在上节算例的基础上,将加强筋的宽度作为变量,研究了加强筋宽度对结构极限承载能力的影响。不同加强筋宽度下结构的极限承载能力计算结果见表3。结构的极限载荷与加强筋宽度关系如图9 所示。

表3 不同加强筋宽度下结构的极限承载能力Tab.3 Ultimatecarrying capacity of structure with different rib width
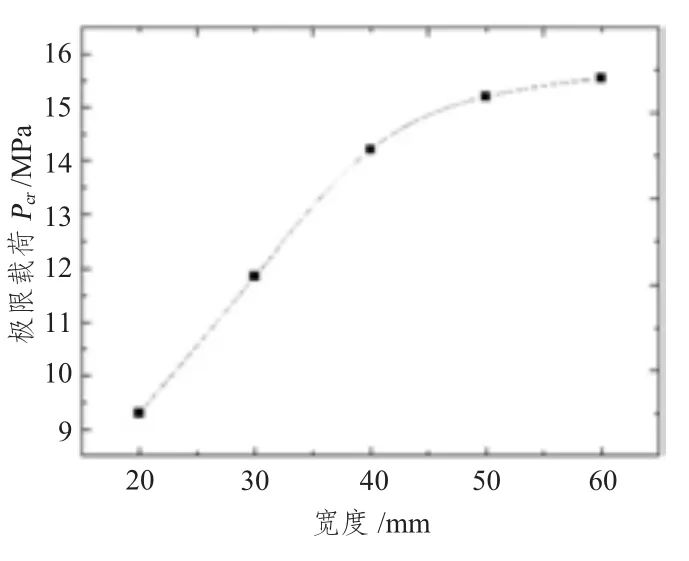
图9 极限载荷与加强筋宽度关系图Fig.9 Ultimatecarrying load against rib width
从图9 可看出,在刚开始阶段即加强筋宽度较小时,增大加强筋宽度,能明显提高结构的极限承载能力,但是随着肋骨宽度的增加,结构极限承载能力增幅逐渐减小,当肋骨宽度由50 mm 增加到60 mm时,结构极限承载能力提高2.3%,提升空间有限。因此,在结构的设计过程中,要综合考虑结构的功能性和经济性,合理地选用加强筋的尺寸。
3.2 加筋布置方案对环肋加筋圆柱壳极限承载能力影响分析
本节在总重量相等的前提下,计算分析3 种加强筋布置方案对加筋圆柱壳极限承载能力的影响,如图10 所示。

图10 典型加筋布置方案Fig.10 Typical arrangements of rib
3 种布置方案下加筋圆柱壳的极限承载能力计算结果见表4。

表4 三种布置方案下加筋圆柱壳的极限承载能力Tab.4 Ultimatecarrying capacity of stiffened cylindrical shell with different arrangements
由计算结果可知,3 种方案下加筋圆柱壳极限承载能力基本相当,方案1 相对方案2 和方案3 略微偏大。因此,在此情况下,可根据内部总布置的需求,灵活选用加强筋的设计方案。
4 结 语
通过对具有宽扁型环肋圆柱壳的强度和稳定性进行计算和分析,得到以下结论:
1)对于宽扁型环肋骨圆柱壳这种特殊的结构形式,采用壳、梁单元进行有限元计算已经不再合适,虽然体单元会花费更多的计算代价,却能准确反映宽扁肋骨耐压圆柱壳结构的真实应力分布;对比分析结果表明采用规范对此类特殊结构进行强度和稳定性计算,会导致较大误差。
2)加筋尺寸及布置方案对结构极限承载能力影响分析结果表明,在本文所选用的尺寸范围内,在加强筋宽度较小时,增大加强筋宽度,能明显提高结构的极限承载能力,但是随着肋骨宽度的增加,结构极限承载能力增幅逐渐减小;在总重量相等的前提下,加强筋的3 种布置方案对结构极限承载能力影响不大,因此,可根据内部总布置的需求,灵活选用加强筋的设计方案。
[1]宋保维,成鹏飞,曹永辉,等.藕节形耐压壳体强度与稳定性有限元分析[J]. 计算机仿真,2007,22(2):54-56.SONG Bao-wei,CHENG Peng-fei,CAO Yong-hui,et al.Strength and stability study of multiple intersecting spheres for pressure hull[J]. Computer Simulation,2007,22(2):54 -56.
[2]黄加强. 长舱段耐压结构研究进展[J]. 船海工程,2014,43(6):175 -177,181.HUANG Jia-qiang. Research development of the long cabin′s pressure structure[J].Ship & Ocean Engineering,2014,43(6):175 -177,181.
[3]王存福,赵敏,葛彤. 水下耐压结构拓扑优化设计方法探究[J].工程力学,2015(1):247 -256.WANG Cun-fu,ZHAO Min,GE Tong.Study on the topology optimal design of under water pressure structure[J].Engineering Mechanics,2015(1):247 -256.
[4]朱邦俊,万正权,徐秉汉,等.半圆环壳型肋骨加强的耐压圆柱壳结构稳定性研究[J]. 船舶力学,2005(1):79-83.ZHU Bang-jun,WAN Zheng-quan,XU Bing-han,et al. On the buckling of cylindrical shell ring - stiffened by halftubes under hydrostatic pressure[J]. Journal of Ship Mechanics,2005(1):79 -83.
[5]吕春雷,王晓天,姚文,等.多种型式肋骨加强的耐压圆柱壳体结构稳定性研究[J].船舶力学,2006(5):113-8.LV Chun-lei,WANG Xiao-tian,YAO Wen,et al. Study of buckling of cylindrical shell ring - stiffened by manifold stiffeners under hydrostatic pressure[J]. Journal of Ship Mechanics,2006(5):113 -8.
[6]龙连春,陈兴华,傅向荣,等.矩形加筋圆柱壳轴压屈曲承载力优化[J]. 中国农业大学学报,2009(4):124-130.LONG Lian-chun,CHEN Xing-hua,FU Xiang-rong,et al.Buckling capacity optimization of cylindrical shell with rectangle stiffeners under uniform axial compression[J].Journal of China Agricultural University,2009(4):124-130.
[7]王林.深海耐压结构型式及稳定性研究[D].北京:中国舰船研究院,2011.WANG Lin. Studies on deep - sea pressure structuraltype and stability [D]. Beijing:China Ship Research &Development Aca de my,2011.
