基于骨架图匹配的汉字变形技术

刘敏，詹华年，梁晓辉*，胡佳佳

(1.北京航空航天大学 计算机学院，北京100191;2.北京师范大学 文学院，北京100875)

汉字是一种典型的表意语言，每一个字符都由一个象征性的书写符号来表示.在它漫长的发展历史当中，汉字共经历5个主要阶段:甲骨文、金文、小篆、隶书和楷书.虽然形状和拓扑发生了极大的改变，但是这些阶段之间是相互关联的.其中前3种统一称作古文字，而后2种称作今文字.对语言文字研究可以分为共时与历时2个方向.共时是指研究语言在特定事件的情况，而历时是指研究语言在较长历史时期所经历的变化.如果能够理解演化的过程，将对汉字历时研究起到重要的作用［1］.汉字演化过程中的变化主要包括:①笔画形状的改变;②汉字拓扑结构的改变;③部分增加或减少.在本文中主要工作在于利用汉字过程中保持不变的特征进行汉字的匹配对应，并用于生成尽可能平滑的变形结果，为汉字历时研究和汉字教育提供技术基础.

形状变形是指在源形状与目标形状之间建立平滑的变化过程，它是计算机图形学中的重要技术，并广泛应用于电视、电影特效，卡通动画和表面重构等工作.它主要包括2个步骤:①对应.建立源形状与目标形状之间的对应关系.②路径插值.计算中间形状的位置.

为了形成准确的匹配结果人们已经做了大量的工作.文献［2］中提出基于物理的方法，其核心是将2个多边形看作线框，多边形之间的渐变过程被看作初始线框变化到目标线框的过程，而线框之间的变化做功可分为伸缩和弯曲做功2部分，通过最小化做功函数来建立顶点对应关系.文献［3］中通过形状顶点所构成的三角形间的相似度来建立对应.以上方法都通过使用角度、边长和三角形区域等几何性质来建立源形状与目标形状之间的对应关系.然而，这些性质与其形状所代表的含义毫无关系，因此这类方法不能建立使人满意的对应结果.另一些方法使用半自动的方式建立对应文献［4-5］，这类方法处理复杂图像时人的工作难度大大增加，耗时耗力.其他方法采用局部特征进行匹配，如文献［6］用均匀采样产生的点集合表示形状，用每一个采样点与其他点的相对位置关系表示该点的特征.文献［7］中的特征点用主成分分析(PCA)的方法进行描述，特征点的形状性质包括计算凹凸性、梯度方向.文献［8-9］获取近似的骨架描述形状，并通过匹配骨架建立顶点的对应.

已经有相关研究运用点集合定位［10-11］等算法进行现代汉字的变形，然而这些方法处理范围并不包括不同阶段汉字之间的变形，不适用于处理演化过程中的复杂变化.一方面，汉字由部件组成，部件通常包含独特的结构.只采用局部形状特征的方法无法表现出一个整体的特点.另一方面汉字的拓扑结构也在发生着改变，简单的拓扑变化无法满足汉字变形的需要.为此本文提出一种基于骨架的图匹配方法来解决汉字中的对应问题.该方法的基本思路是通过比较所选取的特征点间的最短笔画路径来决定最优匹配.这与文献［9］中的思路相似，但是本文的方法比它更适合处理汉字间的问题.这种方法与直接比较骨架拓扑结构的传统方法相比，复杂度低，速度更快，易于找到两汉字中最相似的部分而不受多余部分干扰.对应产生之后，本文使用尽可能刚性的插值方法［12］产生渐变动画.

1 骨架图匹配

在汉字研究中，细化后的骨架仍然保留了汉字的语义和结构信息，因此本文直接对骨架进行处理而不是轮廓.骨架图匹配是用一种基于骨架的图模型匹配方法.骨架通常用属性关系图表示，通过找到属性关系图的最优匹配来产生对应关系.

1.1 构造属性关系图

首先依次使用Zhang-Suen快速并行细化算法［13］和 Shi-Tomasi角点检测方法［14］提取骨架和特征点.然后以特征点作为顶点，特征点间的笔段作为边构造属性关系图，如图1所示.具体细节如下.

1)两个相邻特征点之间的笔段为图的一条边，边可以根据它的方向分为横、竖、撇、捺4种类型.这4种类型普遍存在于汉字的各个阶段当中，并且有自己的方向(0°，90°，135°和 45°).这里使用线性回归计算笔段方向，并判断笔段类型，允许有±15°的差异.笔段分类后骨架变为一个有向无环图.

2)特征点作为图的顶点，它可以分为3种类型.入度为0，出度不为0的顶点叫做起始点;入度不为0，出度为0的点叫做终止点;既不为起始点也不为终止点的点称作连接点.

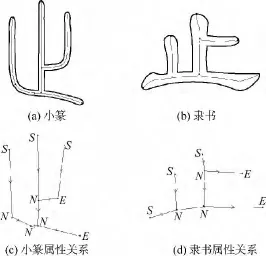
图1 小篆与隶书的字“止”及其属性关系图Fig.1 “Zhi”and its attributed-relation graph in seal script and clerical script

1.2 骨架图匹配

通过建立起始点和终止点的对应关系来匹配2个图模型，因为这些点一般都是本文书写时的起点和终点，而连接点并没有参与匹配.接下来先介绍匹配中的相似度度量方式.

假设有I个起始点和J个终止点在图G中，I′个起始点和 J′个终止点在图 G′中.ui(i=1，2，…，I)，vi′(i′=1，2，…，I′)分别表示 2 个模型中的起始点，uj(j=I+1，I+2，…，I+J)，vj′(j′=I′+1，I′+2，…，I′+J′)分别表示 2 个模型中的终止点.同类点间的相似度用欧式距离表示，公式如下:

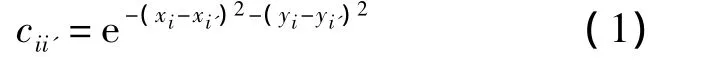
其中x，y为归一化到［0，1］后的坐标值.

一个起始点到一个终止点的最短路径由p(ui，uj)表示，本文记录 p(ui，uj)中的笔画类型(横、竖、撇、捺)和顺序作为笔画路径 ps(ui，uj)，如图2所示.那么任意2个路径的相似度表示为

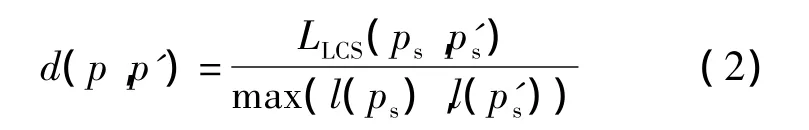
式中，LLCS为2个序列的最大公共子序列的长度;l为序列的长度.

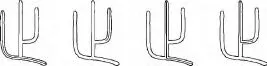
图2 起始点与终止点间的笔画路径Fig.2 Stroke-paths between startpoints and endpoints

由以上2个相似度方程，可以将对应问题转化为求解最优匹配问题.先假设一个匹配矩阵M，mii’∈{0，1}，mii′=1 表示图 G 中的 ui匹配到G′中的 vi′，mii′=0 则表示不匹配.并且 M 的纵向之和与横向之和都为1，确保G与G′之间的匹配一一对应.相似度方程可以写为

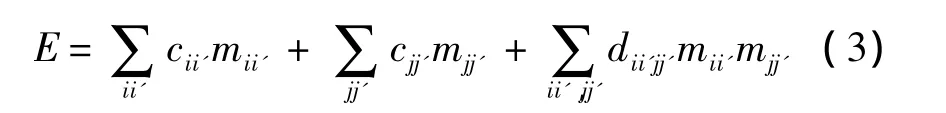
式中c和d分别用式(1)和式(2)计算.目标是寻找最优匹配，最大化该方程，使用双分解方法［15］求解.对应结果在图3中显示，图3(a)的结果可以由本文的算法直接得到，图3(b)的结果需要通过2.2节的步骤得到.

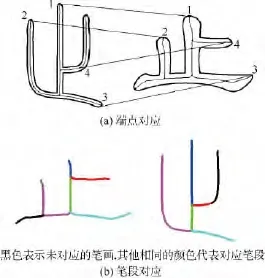
图3 小篆与隶书笔画的对应结果Fig.3 Correspondence results between seal script and clerical script

2 变形动画

本节将介绍使用骨架图匹配进行汉字变形的具体方法.本文的方法主要包括以下3个步骤:①部件分割.输入待变形的2个汉字，用半自动的方式分割和匹配部件.②笔画对应.对部件进行骨架提取，拆分笔段后使用骨架图匹配算法进行匹配，产生顶点和笔段的对应关系.③形状插值.根据对应结果对2个汉字同构三角化，并使用尽可能刚性的形状插值产生动画.

2.1 部件分割

除了独体字外，汉字通常由2个以上部件组成.比如“堤”字有“土”字和“是”组成，如图4所示.因此有必要首先分析汉字找到部件的结构特点.为了获取对应的部件使用最小包围盒去分割输入的不同时代汉字，并根据最小包围盒之间的相对位置构造汉字的块模型［16］，如图5所示.之后，在块模型中位于相同位置的部件就是匹配的部件.然而由于部件间可能会有交叉、粘连等情况出现，上述方法并不一定能产生正确的匹配结果.因此使用变形模版［17］自动分割部件，并用文献［16］中的人工交互的方式确保结果正确.

图4 小篆(左边)与隶书(右边)的“堤”字的层次结构和对应关系Fig.4 Hierarchical structure and corresponding relationship of“di”in seal script(left)and clerical script(right)

图5 小篆(左边)与隶书(右边)的“堤”字的块模型Fig.5 Block-model of“di”in seal script and clerical script

2.2 笔画对应

在此使用1.2节中介绍的骨架图匹配方法对汉字部件进行对应.在产生图3(a)中的匹配结果后，可以得到笔画路径的对应关系.如 mii′mjj′=1，表示 p(ui，，uj)与 p(vi′，，vj′)对应.每个对应赋予它所经过的骨架点一个属性值wij，，这样所有的骨架点都可以得到一个属性集合，如{w13，w14}.一个字里具有相同属性集合的点划分为同一个笔画，两个字中相同属性的笔画为对应的笔画，如图3(b)所示.为了方便进行形状插值，不匹配的边将与相邻的边合并.

2.3 形状插值

在笔画对应之后，将轮廓点分配到最近的骨架上面，然后采用文献［12］中的插值方法进行路径插值.这个方法对两形状的同构三角形进行插值而不是直接对轮廓点进行插值.为了获得同构三角形，细对应根据之前的笔画对应结果产生.一个笔段有一个起点和一个终点，当它们对应上之后，剩下的点用采样的方式一一对应.这些点用文献［18］中的方法构造同构三角形，如图6(a)所示.然而同构三角形的质量并不好，因此需要采用文献［19］的方法进行优化，产生高质量的同构三角形，优化结果如图6(b)所示.

在构建了同构三角化之后，问题就转化成了对应点的路径插值问题.对于单个三角形，原始三角形记作P=(p1，p2，p3)目标图像顶点记作Q=(q1，q2，q3)矩阵A表示P到Q的仿射矩阵，则

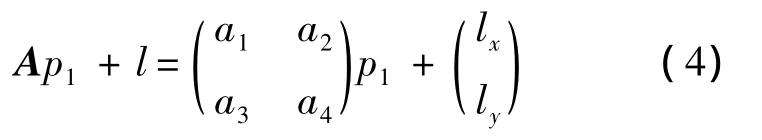
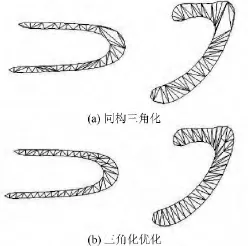
图6 同构三角化和三角化优化的结果Fig.6 Results of compatible triangulations and triangulations optimization

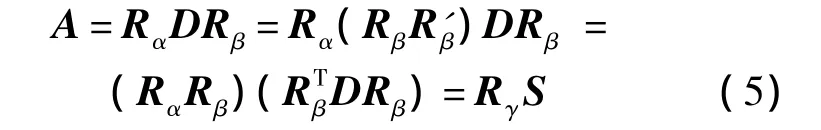
基于这种分解可以得到:

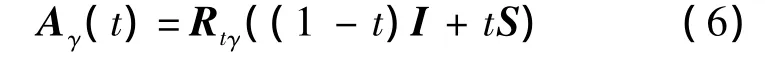
对于三角形集合 T={T{i，j，k}}，每一个初始三角形 P=(pi，pj，pk)与目标三角形 Q=(qi，qj，qk)都有一一对应关系.对于每一对三角形来说，计算一种映射 A{i，j，k}(t).由于大部分的顶点对应于不止一个三角形，所有顶点的映射通常来说不符合各自的最优变换 A{i，j，k}(t).令 V(t)为顶点的期望路径，能够在真实矩阵 B{i，j，k}(t)和期望矩阵A{i，j，k}(t)之间确定最小二次误差，表示如下:

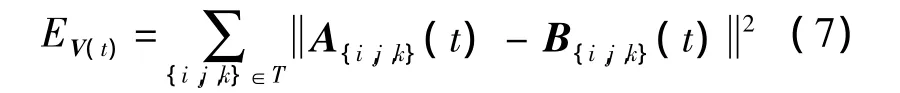
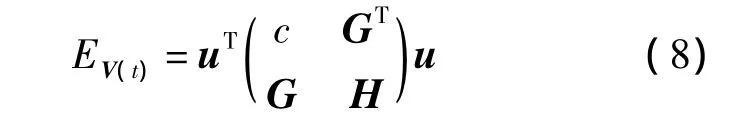
式中，c∈R 表示常数;G∈R2n×1是线性的;H∈R2n×2n为二次型 EV(t)的混合或者单一二次项系数.令自由变量的梯度 ΔEV(t)为0，求解最小值，并对矩阵H求逆，然后利用与G(t)相乘来求解:

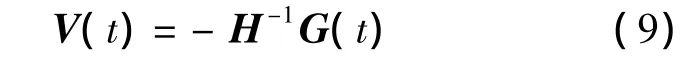
3 实验与结果分析

实验环境为2.66GHz Intel Core Quad CPU和3.0GB DDR2内存，Windows操作系统.算法用Microsoft Visual Studio 2010编程实现.所有的汉字图像分辨率均统一为396×350.实验数据主要是小篆和隶书图片，因为这两种字体是古代汉字与现代汉字的分水岭，文字的变形最剧烈，在汉字演变过程中具有代表性.

为了验证本文方法的效果，将与两种现存方法 比 较:CPD(Coherent Point Drift)［10-11］和 SC(Shape Context)［6］.使用细化算法提取骨架，然后随机采样骨架点作为两个方法的输入.部分试验数据在图7中展示，实验结果在图8中显示.可以看到本文的方法可以精确地找到相似的笔画结构，然而其他两种方法产生了错误的结果.这是因为本文的方法通过搜索笔画路径找到了最相似的部分作为对应结果，适合处理这类问题.

图7 一些小篆与隶书的例子Fig.7 Some examples in seal script and clerical script

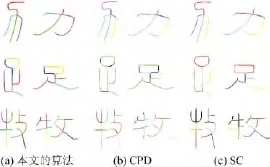
图8 对应算法的实验结果Fig.8 Experimental results of correspondence algorithms

最终，变形动画也依据对应结果产生，结果在图9中展示.实验当中的汉字变形非常复杂，根据笔画情况可分为:①笔画数量增多的情况;②笔画数量不变的情况;③笔画发生巨大变化的情况.结果表明本文的方法可较好地解决这些问题.

图9 小篆到隶书的变形动画Fig.9 Morphing animation from seal script to clerical script

4 结论

本文提出了基于骨架的图匹配算法解决汉字对应问题，并将它应用于不同时期间的汉字变形问题上.结果表明本文的方法具有一定效果，但是该方法仍有局限性:①笔画相似度的度量依赖于骨架和笔画提取的效果.②本文的方法不适用于笔画变化极大的问题.将在未来继续研究相关问题并改进算法，用于推动汉字的文化教育与国际传播.

References)

［1］ 王宁.汉字构形史丛书［M］.上海:上海教育出版社，2003.Wang N.Series of books:history of Chinese characters’structure［M］.Shanghai:Shanghai Education Press，2003(in Chinese).

［2］ Sederberg T W，Greenwood E.A physically based approach to 2D shape blending［C］//ACM Computer Graphics.New York:ACM，1992，26(2):25-34.

［3］ Zhang Y.A fuzzy approach to digital image warping［J］.IEEE Computer Graphics and Applications，1996，16(4):34-41.

［4］ Carmel E，Cohen-Or D.Warp-guided object space morphing［J］.The Visual Computer，1997，13(9-10):465-478.

［5］ Yang W W，Feng J Q，Jin X G，et al.2-D shape blending based on visual feature decomposition［C］//Proceedings of Computer Animation and Social Agents，2004:139-146.

［6］ Belongie S，Malik J，Puzicha J.Shape matching and object recognition using shape contexts［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2002，24(4):509-522.

［7］ Liu L G，Wang G P，Zhang B，et al.Perceptually based approach for planar shape morphing［C］//12th Pacific Conference on Computer Graphics and Applications.Washington:IEEE，2004:111-120.

［8］ Mortara M，Spagnuolo M.Similarity measures for blending polygonal shapes［J］.Computers ＆ Graphics，2001，25(1):13-27.

［9］ Bai X，Latecki L J.Path similarity skeleton graph matching［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2008，30(7):1282-1292.

［10］ Myronenko A，Song X.Point set registration:coherent point drift［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32(12):2262-2275.

［11］ Lian Z H，Xiao J G.Automatic shape morphing for Chinese characters［C］//SIGGRAPH Asia 2012 Technical Briefs.New York:ACM，2012，2:1-4.

［12］ Alexa M，Cohen-Or D，Levin D.As-rigid-as-possible shape interpolation［C］//Proceedings of the ACM SIGGRAPH Conference on Computer Graphics.New York:ACM，2000:157-164.

［13］ Zhang T，Suen C Y.Fast parallel algorithm for thinning digital patterns［J］.Communications of the ACM，1984，27(3):236-239.

［14］ Shi J B，Tomasi C.Good features to track［C］//Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Los Alamitos，CA:IEEE，1994:593-600.

［15］ Torresani L，Kolmogorov V，Rother C.Feature correspondence via graph matching:models and global optimization［C］//Proceedings of the 10th European Conference on Computer Vision.Heidelberg:Springer Verlag，2008:596-609.

［16］ Xia Y，Wu J Q，Gao P C，et al.Ontology-based model for Chinese calligraphy synthesis［J］.Computer Graphics Forum，2013 32(7):11-20.

［17］ Chung F，Ip W W S.Complex character decomposition using deformable model［J］.IEEE Transactions on Systems，Man and Cybernetics Part C:Applications and Reviews，2001，31(1):126-132.

［18］ Gupta，H，Wenger R.Constructing piecewise linear homeomorphisms of simple polygons［J］.Journal of Algorithms，1997，22(1):142-157.

［19］ Surazhsky V，Gotsman C.High quality compatible triangulations［J］.Engineering with Computers，2004:20(2):147-156.