拦截弹道快速设计方法

王备，周韬，董长虹

(北京航空航天大学 宇航学院，北京100191)

现代战争要求拦截弹具有快速反应能力，零发射准备时间.在拦截弹的设计过程中，拦截弹道设计是重要的组成部分，通常设计拦截弹道主要是设计一条通过发射点和目标点并满足约束条件的最优拦截弹道，对于拦截弹来说，如何缩短导弹拦截时间，是导弹防御里的一项重要研究内容［1-2］.

拦截弹道优化设计是一个模型高度非线性、时间域跨度大、待优化参数多、约束形式多样化的复杂优化问题，通常采用最优化理论中的参数优化来解决该问题.对于一枚确定的拦截弹，其各项参数包括各级发动机推力、发动机工作时间等都是确定的，其各阶段运动规律基本一致［3-5］.因此对于某一预测命中点，所要解决的就是定点定时到达预测命中点的弹道优化设计问题.一般的优化算法都要通过大量的迭代计算来完成，包括模式搜索法、拟牛顿法、序列二次规划法，以及多种现代启发式算法如遗传算法、粒子群算法等［6-9］，都需要每次代入设计变量，通过弹道计算过程计算优化目标函数以使目标函数越来越趋近于最优，而弹道计算过程中需要通过许多积分运算来计算弹道，所以就会消耗大量的计算时间.这就使导弹不能快速去拦截目标，在实际拦截过程中，就可能失去拦截目标的机会.基于文献［10］提出将人工神经网络应用于制导律设计以及文献［11］提到的将人工神经网络应用于机载实时轨迹优化导引的启发，对于拦截弹这种中间过程规律性较强的弹道优化设计问题，可以尝试运用神经网络来设计弹道.

本文研究如何利用神经网络原理解决快速弹道设计问题.首先对多阶段拦截弹道的优化问题作详细的描述，然后介绍了如何把神经网络应用于快速弹道设计，最后给出了算例仿真和结果分析.

1 拦截弹的数学建模

1.1 动力学模型

拦截弹分为3级，采用固体火箭发动机，从第3级关机点到预测拦截点是无动力飞行阶段.为了简化问题，同时考虑到拦截弹的飞行特性，做出如下假设:

1)假设地球为圆球形;

2)采用USSA76标准大气模型;

3)忽略导弹的侧向运动，即导弹始终在发射点、预测拦截点和地心确定的大圆面内;

4)只考虑导弹弹体的俯仰运动［12］.

基于上述假设可得拦截弹的动力学方程:

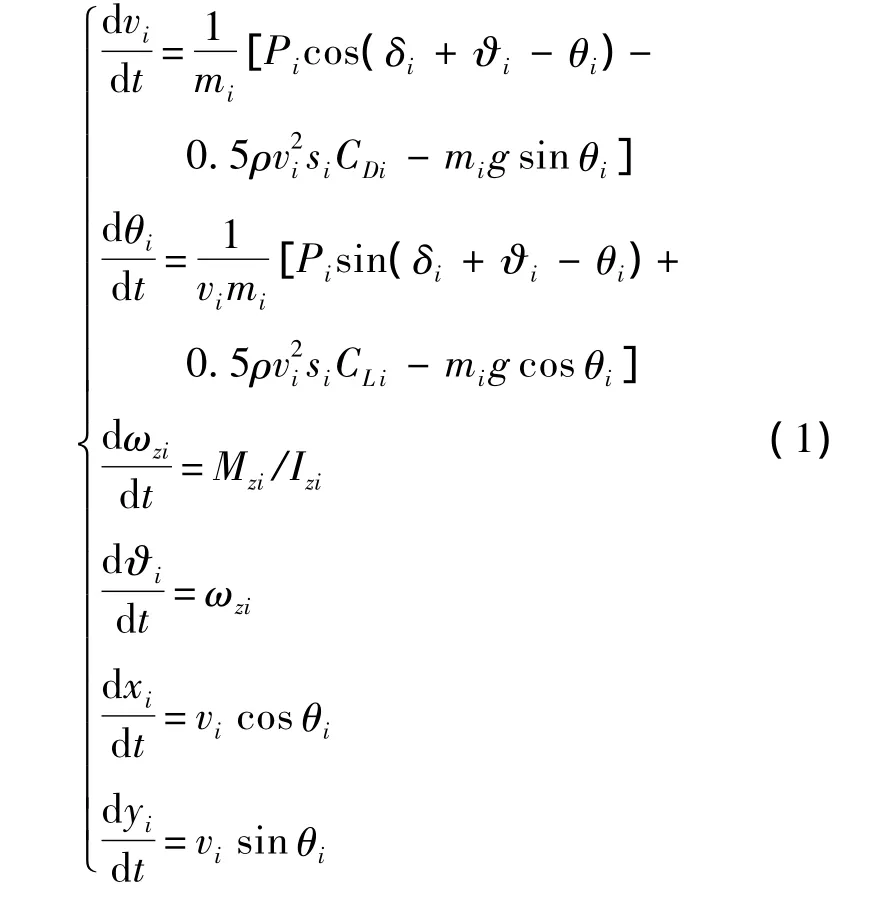
式中，i=1，2，3…为拦截弹飞行的不同阶段;vi，θi，ωi，ϑi，xi，yi为状态变量，分别代表拦截弹的速度、弹道倾角、俯仰角速度、俯仰角和拦截弹的位置坐标;δi为控制变量，代表发动机喷管摆角;Pi为发动机推力;ρ，s分别为大气密度和参考面积;CDi，CLi分别为阻力系数和升力系数;Mzi，Izi分别为俯仰力矩和转动惯量;mi为拦截弹的质量［12］:

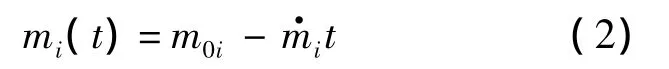
式中，m0i为第 i级起始质量;为推进剂消耗率［12］.

1.2 飞行程序设计

飞行程序是指导弹主动段俯仰角随时间变化的规律，飞行程序的选择是弹道设计的重要组成部分.导弹飞行中的实际俯仰角ϑ(t)与飞行程序角φcx(t)一般是不相等的，但因二者相差甚微，因此弹道计算中可近似认为导弹是按飞行程序角规律飞行的，即ϑ(t)≈φcx(t).

导弹俯仰角ϑ、弹道倾角θ以及攻角α存在如下关系式:

对于依托于气动力转弯的导弹，一般是通过预先给出攻角经验公式α(t)来推求飞行程序角的.但是地基拦截弹的转弯是通过发动机尾喷管有一个摆角，然后对导弹产生一个推力矩，导弹开始转弯.导弹的转弯不是通过气动力矩转弯，所以这里飞行程序角随时间变化的规律是直接给出的［13-14］.

一般单级导弹只进行一次飞行转弯，且转弯设计在亚声速段.因为这里研究的是3级拦截弹，所以设计转弯是经过两次转弯，分别是在一级助推阶段和二级助推阶段.采用的飞行程序角为:一级采用二次曲线型的程序角，二级采用的是等斜率变化的程序角.两次转弯程序角都是设定俯仰角的变化.

飞行程序角的变化规律为

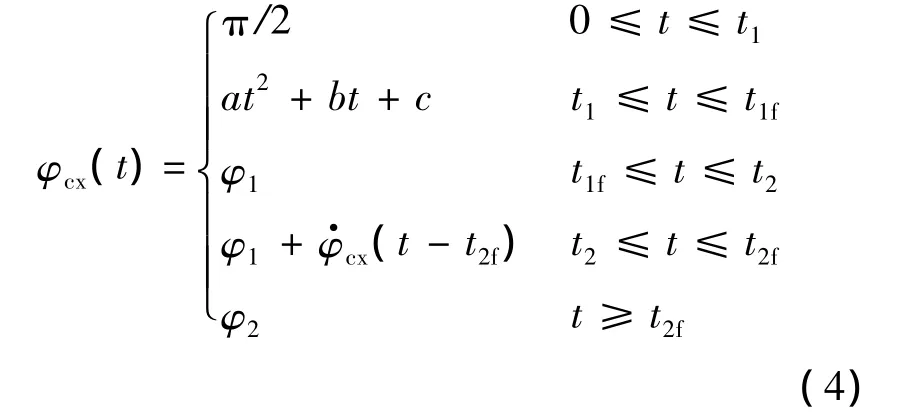
式中，t1，t1f，t2，t2f分别为一级转弯开始时间和结束时间、二级转弯开始时间和结束时间;φ1，φ2为常值，而抛物线方程系数a，b，c和直线斜率可由t=t1f和t=t2f时α=0、俯仰角为定值以及允许俯仰角速度的大小来确定.

为了得到全局最优解，一级转弯开始时间和结束时间全部为固定值，在一级转弯结束时俯仰角达到程序角的最小值，这样可以保证一级转弯时俯仰角的变化是单调下降的.二级转弯开始时间和结束时间也设为固定值，这样在整个飞行阶段程序角的变化如图1所示.从图中可以看出只要改变一级转弯和二级转弯结束时飞行程序角的大小，拦截弹道就会改变.

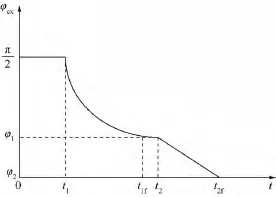
图1 程序角变化曲线Fig.1 Program angle change curve

1.3 弹道优化模型

基于以上原理，并根据实测试验，可以将影响弹道的参数简化为两个参数:飞行程序角φ1，φ2，即一级转弯和二级转弯结束时俯仰角的大小.也就是说，调整这两个参数即可以做到定时到达预测命中点.于是，弹道设计问题即可以用参数优化来实现.

1)优化目标.

目标函数f(φ1，φ2)为被动段结束时导弹位置与预测命中点的距离最小.

2)设计变量.

优化设计变量为两个飞行程序角φ1，φ2，且φ1≥φ2.

3)约束条件.

初始状态约束:拦截弹在初始发射阶段有垂直段，因此初始状态要满足:

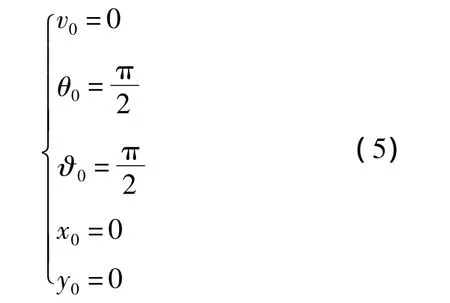
时间约束:一级转弯开始时间和结束时间、二级转弯开始时间和结束时间、三级主发动机工作时间均为固定值.

摆角约束:最大允许喷管摆角为δmax，则

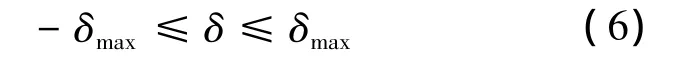
状态连续性约束:

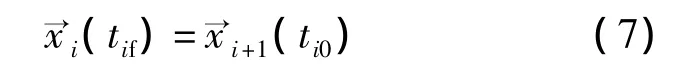
2 基于神经网络的快速弹道设计

2.1 基于神经网络的快速弹道设计原理

神经网络是一种模仿生物神经网络的结构和功能的数学模型，这种算法可以直接建立一种输入和输出的简单映射关系，而不管中间的计算过程［15］.使用神经网络建立参数优化模型可以避开繁琐的计算过程，这样就节省了时间，在弹道设计的过程中达到快速的目的.神经网络可以事先在导弹的射程区间内采样，然后通过样本学习其中的规律，将规律贮存于神经网络的权值和阈值之中，而神经网络的计算过程中只有输入量与权值阈值之间简单的乘法和加法运算，所以给出输入量即可迅速计算出对应最优的设计变量.

对于定点定时到达预测命中点的弹道优化设计问题，只要输入目标点信息(包括目标位置和拦截弹飞行时间)，就可以用传统优化算法确定拦截弹道飞行程序角的参数，从而得到拦截弹道.这是一般弹道优化设计的方法，其流程图如图2所示，从图中可看出每一次迭代都要调用一次弹道计算程序，若每调用一次弹道计算程序耗时约T(单位:s)，共迭代N次，则整个弹道设计流程共耗时约(N+1)T.

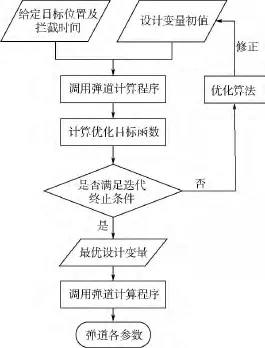
图2 传统优化算法的弹道设计流程图Fig.2 Trajectory design flow chart using general optimization algorithm

将神经网络应用于拦截弹道设计中，则其流程图如图3所示.神经网络的样本计算和样本训练可以提前在线下完成，而对于训练好的神经网络，输入目标点信息，就可以通过神经网络中输入与输出间的简单映射关系一步计算得到最优设计变量，从而得到拦截弹道.从图3中可看出该过程只调用一次弹道计算程序，所以共耗时约T，比传统优化方法降低NT.

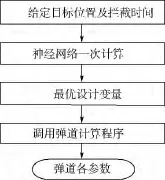
图3 应用神经网络的弹道设计流程图Fig.3 Trajectory design flow chart using neural network

2.2 神经网络样本的生成

根据前面所述，样本数据中输入参数为目标点信息(包括目标距离、目标高度、拦截时间)，输出参数为最优飞行程序角(φ1，φ2)，共5个参数.其中目标距离和目标高度根据拦截弹的拦截空域来确定，且样本范围尽量取满整个拦截空域，来使神经网络的应用更加有效.拦截时间也并不是随便选取，而是需要确定拦截时间的边界，利用一维搜索法(黄金分割法等)确定满足约束条件的最小飞行时间和最大飞行时间，然后从中选取.只要有了目标点数据，就可以用一般的优化算法确定拦截弹最优飞行程序角的参数.最后把每一组输入参数和输出参数作为一组数据，而拦截空域内的多组数据则组成一个训练样本.

2.3 神经网络设计

这里采用的是一种最常用的误差反向传播(BP)神经网络.根据样本数据中输入输出个数，建立一个3个输入、2个输出的神经网络，所建立的神经网络包含2层隐层，第1隐层神经元个数为8个，第2隐层神经元个数为6个，输出层神经元个数为2个.第1隐层和第2隐层的神经元传递函数均为正切S型函数(tansig)，输出层的神经元传递函数为纯线性函数(purelin).

建立的3个输入、2个输出的神经网络结构图如图4所示，其中w表示权值，b表示阈值.

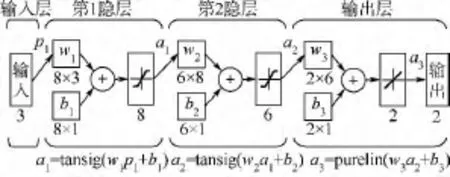
图4 BP神经网络结构Fig.4 BP neural network structure

根据所设计的BP神经网络和样本，用训练算法(这里采用Lenvnberg-Marquandt算法)对神经网络进行训练，得到最终的权值和阈值.根据所建立神经网络的运算关系和训练后的权值和阈值，给出输入，即可快速计算得到相应输出.

3 算例仿真

本文算例采用如下初始条件:拦截弹初始位置(0，0)，预测拦截点坐标(1 172，721)(单位:km).射程d=500～1500km，拦截高度范围取h=500～1500km，初始速度V=0m/s，初始弹道倾角θ=π/2，初始攻角 α =0°.喷管摆角约束 δmax=10°，δmin=10°.拦截弹主动段共有 3 级，发动机的工作时间分别为:第1级69 s，第2级70 s，第3级68 s.为计算方便发射时间定为零时，目标在331 s时刻到达预测命中点.

在射程和射高范围内得到480组样本数据，神经网络训练结果如图5所示，经过424次训练后训练停止，训练误差精度在418次达到最好，为0.0081621，从图中可以看出结果合理，神经网络训练达到预期效果.图6是对网络输出和相应的期望输出向量进行线性回归分析，可以看出训练数据的跟踪效果很好，线性回归相关系数R=0.99997.

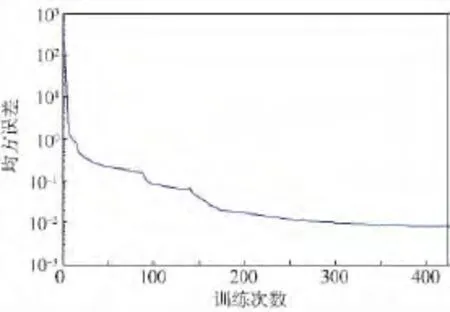
图5 神经网络训练均方误差Fig.5 Mean squared error of neural network training

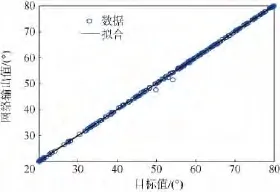
图6 训练数据线性回归结果Fig.6 Linear regression results of training data

图7和图8分别为拦截弹道曲线和拦截弹速度曲线，可以看出神经网络设计的弹道与理论弹道基本一致.表1中对比了粒子群算法与神经网络的计算结果，数据表明虽然神经网络计算得到的与预测命中点偏差较大一些，但此命中精度依然较为良好，而相比仿真时间，神经网络所需的仿真时间极短.

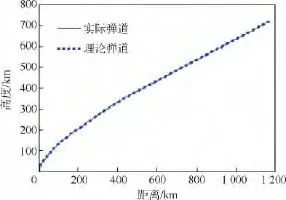
图7 拦截弹道曲线Fig.7 Intercept trajectory curve

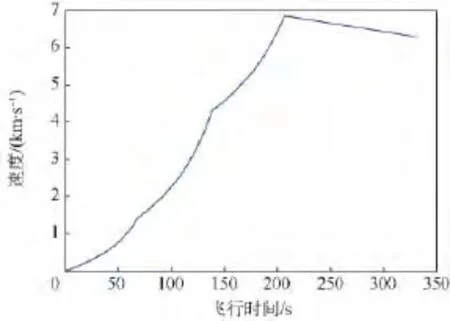
图8 拦截弹速度曲线Fig.8 Velocity curve of interceptor

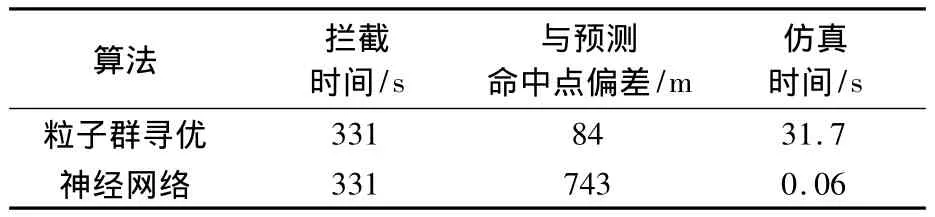
表1 仿真算例结果清单Table1 Results list of simulation example

在拦截射程和高度范围内随机选取预测拦截点，对于用神经网络算法设计弹道的与预测命中点偏差进行500次蒙特卡洛仿真，结果如图9所示.从图中可看出预测命中偏差均在2 km以内，平均值为0.53km，这样的误差在实际作战中足够让拦截弹的弹头找到并准确击中目标，说明神经网络应用于弹道设计的方法是有效的.部分不同拦截点下的结果对比如表2所示.

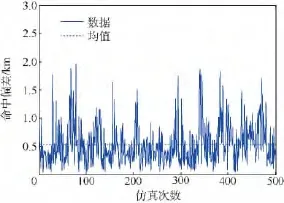
图9 不同拦截点的蒙特卡洛仿真Fig.9 Monte Carlo simulation in different intercept points

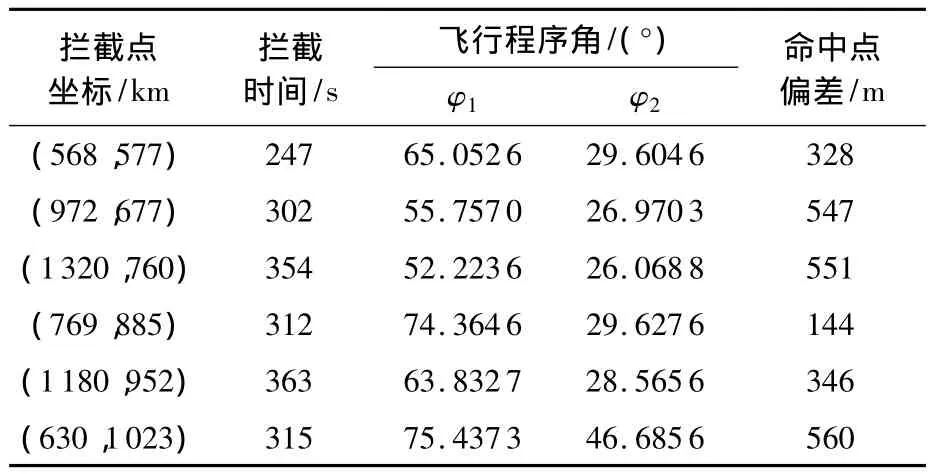
表2 不同拦截点下的部分结果对比Table2 Some results comparison in different intercept points

4 结论

本文建立了拦截弹的动力学模型、飞行程序和弹道优化模型，并在分析神经网络计算原理的基础上提出了一种新的拦截弹的快速弹道设计方法，经过仿真实例验证表明:

1)该方法相比传统算法设计的拦截弹弹道偏差稍大，但依然有良好的命中精度.

2)该方法在设计拦截弹道时的计算时间得到极大的缩短，有效地实现了快速设计弹道.

References)

［1］ 王静.动能拦截弹技术发展现状与趋势［J］.现代防御技术，2008(4):23-26.Wang J.Current technology and development trend of kinetic missiles［J］.Modern Defence Techonlogy，2008(4):23-26(in Chinese).

［2］ 刘燕斌，南英，陆宇平.弹道导弹突防策略进展［J］.导弹与航天运载技术，2010(2):18-23.Liu Y B，Nan Y，Lu Y P.Evolvement of penetration strategies for ballistic missiles［J］.Missiles and Space Vehicles，2010(2):18-23(in Chinese).

［3］ Foreman C D，Tournes H C，Shtessel B Y.Interceptor missile control:a new look at boost and midcourse，AIAA-2010-7579［R］.Reston:AIAA，2010.

［4］ Chen H R，Speyer L J，Lianos D.Optimal intercept missile guidance strategies with autopilot lag［J］.Journal of Guidance，Control and Dynamics，2010，33(4):1264-1272.

［5］ Shima T，Golan M O.Exo-atmospheric guidance of an accelerating interceptor missile，AIAA-2008-6494［R］.Reston:AIAA，2008.

［6］ Anderson M B，Burkhalter J E，Jenkins R M.Design of a guided missile interceptor using a genetic algorithm［J］.Journal of Spacecraft and Rockets，2001，38(1):28-35.

［7］ Betts J T.Survey of numerical methods for trajectory optimization［J］.Journal of Guidance，Control and Dynamics，1998，21(2):193-207.

［8］ 陈阳阳.飞行器总体参数和弹道优化方法研究［D］.哈尔滨:哈尔滨工程大学，2013.Chen Y Y.Research on optimization design method of aircraft overall parameters and trajectory［D］.Harbin:Harbin Engineering Univercity，2013(in Chinese).

［9］ Sobieszczanski S J，Haftka T R.Multidisciplinaryaerospace design optimization:survey of recent developments，AIAA-1996-0711［R］.Reston:AIAA，1996.

［10］ Johnson N E，Calise J A，Corban J E.Reusable launch vehicle adaptive guidance and control using neural networks，AIAA-2001-4381［R］.Reston:AIAA，2001.

［11］ Mateen D Q，He L S.Rapid trajectory optimization using computational intelligence for guidance and conceptual design of multistage space launch vehicles，AIAA-2005-6062［R］.Reston:AIAA，2005.

［12］ 刘士明，董长虹，周韬.基于高斯伪谱法的时间可变多级拦截弹最优弹道设计［J］.战术导弹技术，2013(3):32-36.Liu S M，Dong C H，Zhou T.Time variable multi-phase trajectory optimization for interceptor using Gauss Pseudo-spectral method［J］.Tactical Missile Technology，2013(3):32-36(in Chinese).

［13］ 张毅，肖龙旭，王顺宏.弹道导弹弹道学［M］.长沙:国防科技大学出版社，2005:293-305.Zhang Y，Xiao L X，Wang S H.Ballistic missile ballistics［M］.Changsha:National University of Defense Technology Press，2005:293-305(in Chinese).

［14］ 郝磊，李邦杰，王明海.速燃弹道导弹飞行程序角设计方法［J］.弹道与制导学报，2008(2):180-182.Hao L，Li B J，Wang M H.Study on the flight program angle design of ballistic missile based on fast burn motor［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2008(2):180-182(in Chinese).

［15］ 张德丰.MATLAB神经网络应用设计［M］.2版.北京:机械工业出版社，2012:136-158.Zhang D F.MATLAB neural network application design［M］.2nd ed.Beijing:China Machine Press，2012:136-158(in Chinese).