基于延迟决策的航空公司动态价格竞争复杂性

胡 荣，李天睿，张 君，江 超

（南京航空航天大学民航学院，南京210016）

0 引言

航空运输市场是典型的寡头垄断市场，航空公司在市场价格竞争过程中存在着明显的决策信息交互作用：航空公司在制定定价策略时，不仅要考虑策略对自身的影响，还要考虑到竞争对手对自身定价策略的态度和反应。因此，博弈论成了此类问题的有效分析工具。

由于定价问题涉及到航空公司的核心利益，很多学者已尝试运用博弈论来分析航空公司的市场价格竞争行为，主要沿着两条主线展开：一是以收益管理理论为基础开展分析。文献［1］在第六届INFORMS收益管理和定价年会上，提出了非零和的和非合作的随机博弈和微分博弈的动态定价模型，并证明了纳什均衡解的存在性和唯一性；文献［2］构建了市场中包含两家航空公司，采取两种定价水平的博弈模型，分析了中国航空公司收益管理效果不明显的影响因素；文献［3］通过引入社会福利函数和航空公司载运率因子，运用次优理论对机票价格管制问题进行了博弈分析和理论解释；文献［4］则结合中国航空定价机制，引入民航总局这一市场监管者，运用博弈理论分析了民航总局对航空定价实行管制和航空公司降价竞争的问题；文献［5］对航空市场的差别定价问题进行了分析，等等。二是以平均定价理论为基础开展分析。文献［6］较早运用博弈论研究了航空公司价格竞争问题，文章分别构建了完全信息和不完全信息的价格竞争博弈模型，分析了航空公司之间恶性价格竞争的缘由；文献［7］构建了航空公司两阶段的市场空间博弈模型，并对South－Atlantic航空市场进行了分析；文献［8］基于产品差异化理论，建立了不完全信息的航空公司价格竞争博弈模型，证明模型不存在纯战略均衡；文献［9－11］分别考虑了航班延误、进入壁垒的因素，构建了航空公司市场竞争的动态博弈模型；文献［12］对中国航空运输市场的“价格战”和“价格联盟”进行了分析，对东方航空公司和南方航空公司间的“价格战”进行了模拟和分析；文献［13－14］研究了基于有限理性和不同竞争战略的航空公司动态价格竞争复杂性，等等。

纵观当前研究文献，运用博弈论开展航空公司价格竞争的研究尚有几点不足：1）绝大多数研究均假设航空公司在价格竞争中具有完全理性；2）是对航空公司的价格竞争研究以静态分析为主，动态价格竞争研究不足；3）是对航空公司市场价格调整机制的研究尚显单一，尚未涉及延迟决策机制。故本文在上述研究不足的基础上，引入延迟决策价格调整机制，建立双寡头垄断的航空公司动态价格竞争模型，对模型均衡点的存在性与稳定性进行分析，并仿真不同市场参数下的航空公司动态价格竞争复杂性，深入研究延迟决策对系统稳定域、系统到达均衡的时间、航空公司累计利润等的影响，以从不同视角分析延迟决策对竞争复杂性的影响。

1 基本模型

收益管理在国外航空公司中有着广泛运用，通过对细分的旅客实施差别定价可提高航空公司的收益。但中国航空运输市场65%以上的旅客是公务和商务旅客，从收益管理的角度来看，中国当前的航空旅客需求是比较缺乏弹性的，缺乏实施差别定价的市场基础［3］，同时中国航空公司的收益管理软件主要用于统计和成本效益分析等方面，收益管理并未发挥其有效作用［4］，因而本文采用文献［13］中平均价格定价理论构建航空公司动态价格竞争模型。

假定某航空运输市场仅由两家航空公司（分别记为A1和A2）所垄断，并且两家航空公司都以利润最大化为战略目标制定竞争策略。不妨设航空公司Ai在时期t的机票价格为pi（t），旅客运输量为qi（t），其中i＝1，2，t＝0，1，2，…，下同。则可得到整个航空运输市场的需求函数为

其中，i，j＝1，2，i≠j；ai＞0表示航空运输市场对航空公司Ai的需求水平；θi＞0称为差异化系数，反映的是航空公司之间的差异化程度。具体而言，差异化系数θ1表示航空公司A2对A1的差异化程度，θ1越小表明两者差异化程度越大，替代性越小。一般而言，有0＜θi＜bi，这意味着某航空公司自身价格对市场需求的影响大于交叉价格的影响。考虑到航空公司间在航线网络、航班班次、服务品牌等方面的差异且不失一般性，令a1＝a2，b1＝b2，θ1≠θ2则市场需求函数为

假设两家航空公司的成本函数均为线性形式即Ci＝ciqi。则航空公司在时期t的利润函数为

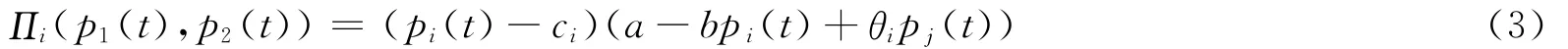
对于任意给定的时期t，对Πi（p1，p2）关于pi求偏导，可得到航空公司Ai在当期的边际利润为

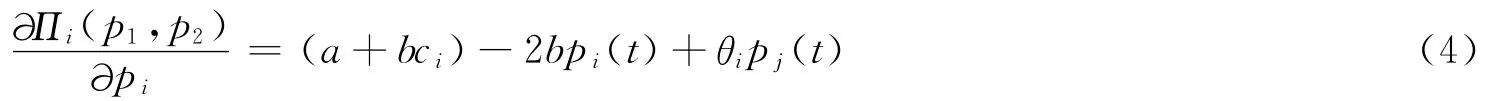
由于在现实市场竞争中，航空公司并不能获得完全的市场信息，也不能完全预测到未来的市场变化情况，因而他们在价格竞争决策中体现为有限理性，只能随着价格竞争的进程按照一定的价格调整规则对自身价格进行动态调整直至竞争最终达到均衡状态。而“近视眼”调整机制是市场竞争中最为常用的调整机制之一［15］。本文假定两家航空公司均采用“近视眼”调整机制，即航空公司基于上期价格竞争的边际利润情况，对本期价格决策进行的动态调整。具体调整规则为：在时期t，如果估计的边际利润是正（负）的，那么该航空公司将提高（降低）第t＋1期的价格。故有：

其中，αi＞0为航空公司Ai的价格调整速度，反映了该航空公司对边际利润信号的反应速度。因此可得基于“近视眼”调整机制的航空公司动态价格竞争模型：

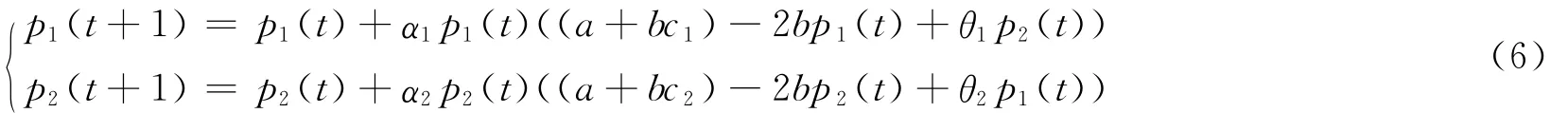
然而在现实中，航空公司在制定价格决策时不仅会考虑到当期的利润情况，还会综合考虑以往连续多期的利润信息；此外，航空公司在动态价格竞争过程中一旦操作失当将会使得市场竞争陷入混沌［13－14］，航空公司必定会采取措施来稳定市场。本文根据上述思想，可构建基于延迟决策的航空公司动态价格竞争模型：

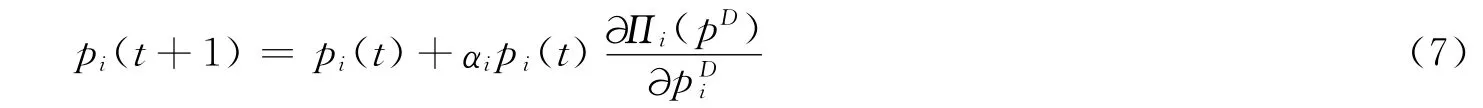
本文一方面为重点考察延迟决策对航空公司动态价格竞争的影响，另一方面为体现航空公司间决策能力的差异，不妨认为航空公司A1具有较高的市场竞争能力，采用延迟决策参与市场价格竞争，而航空公司A2仅采用“近视眼”调整机制参与市场竞争。因此当T＝1时则有如式（8）航空公司动态价格竞争模型：

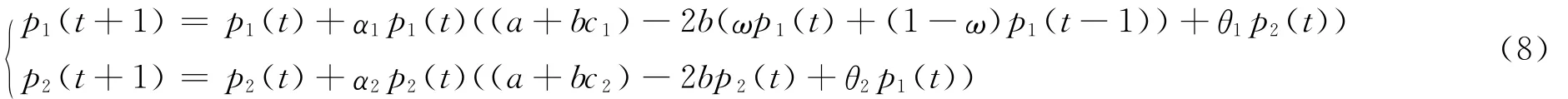
2 模型分析

对于航空公司的价格竞争，只有当其均衡价格非负时才有现实意义，故本文只研究模型（8）的均衡结果非负的情况。为研究模型（8）的稳定性，将其改写为

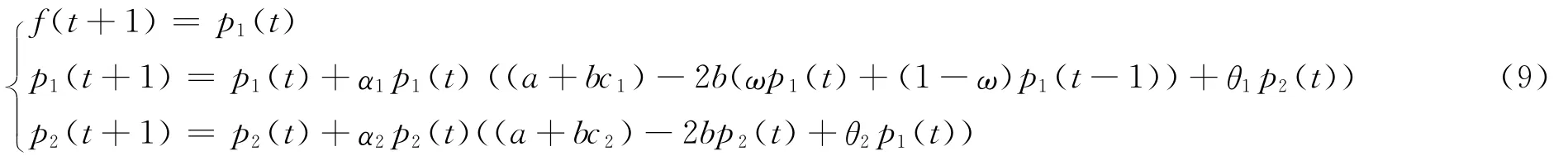
首先，计算系统（9）在任意一点的Jacobian矩阵：

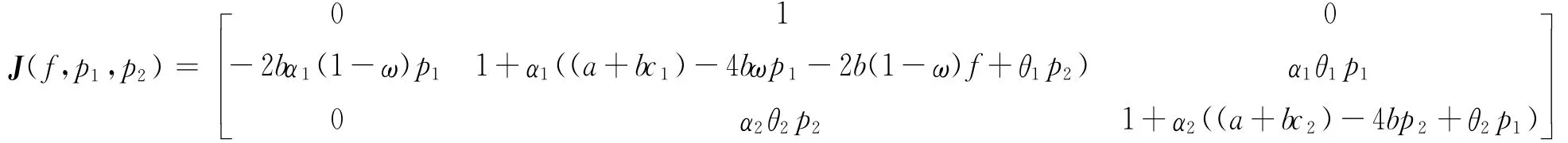
在有界均衡点E1处的Jacobian矩阵为

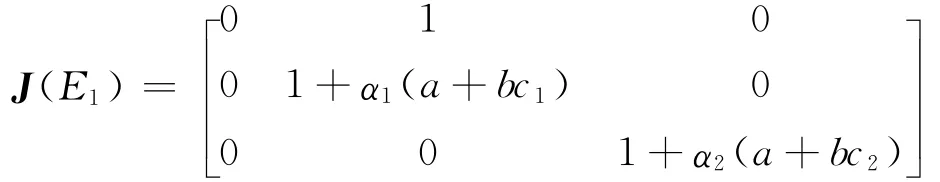
它的3个特征值分别为λ1＝0，λ2＝1＋α1（a ＋ bc1）和λ3＝1＋α2（a ＋ bc2）。显然，λ2＞1，λ3＞1，故均衡点E1是不稳定点。

再次，在有界均衡点E2处的Jacobian矩阵为

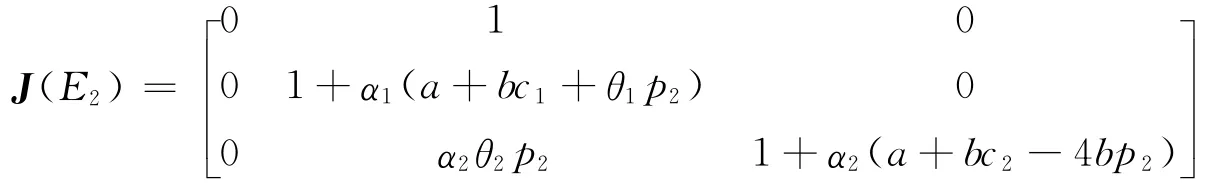
它的3个特征值分别为λ1＝0，λ2＝1＋α1（a＋bc1＋θ1p2）和λ3＝1＋α2（a＋bc2－4bp2）。由于p2＝，故有λ ＞1，λ ＜1，因此均衡点E也是不稳定点。

再次，在有界均衡点E3处的Jacobian矩阵为

它的3个特征值分别为λ1＝1＋α2（（a＋bc2）＋θ2p1），

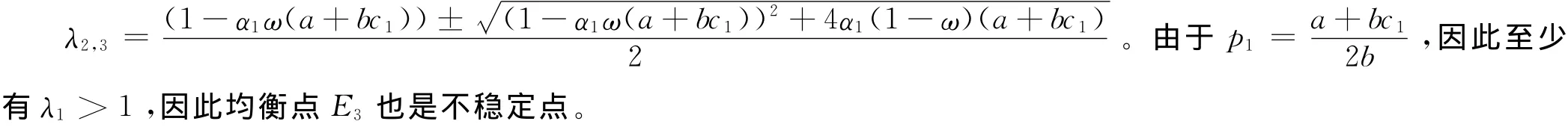
综上分析，可得定理1：

定理1 系统（9）的均衡点E1，E2，E3都是不稳定点。

考察系统（9）在Nash均衡点E＊的情况，考虑到f＊＝p1＊，在均衡点E＊的Jacobian矩阵为

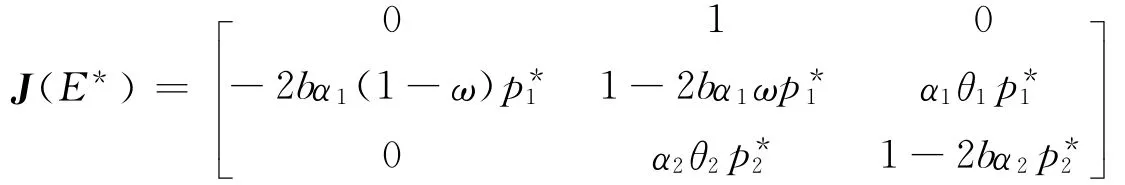
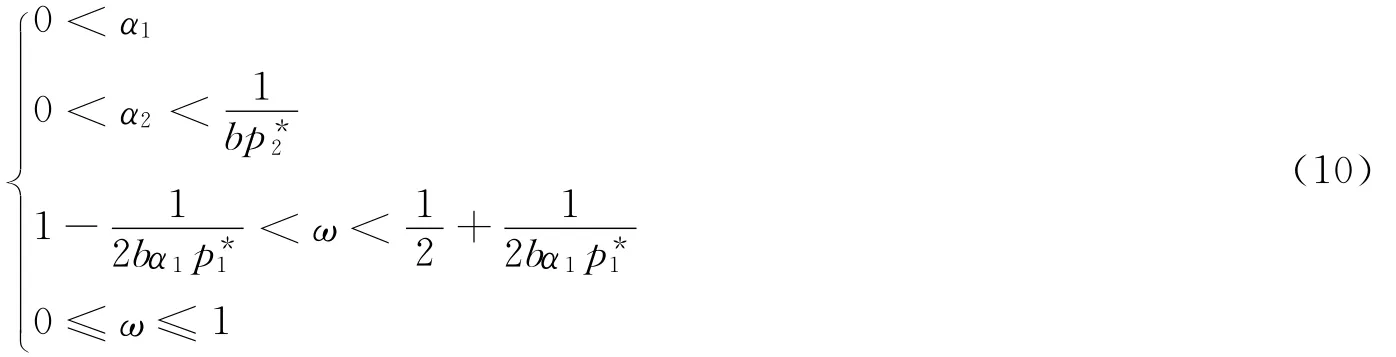
即，式（10）在空间 （α1，ω，α2）中定义了系统（9）的Nash均衡点E＊的一个稳定区域，当系统参数取值超出式（10）这个范围，则点E＊将变得不稳定。因而可得到关于Nash均衡点E＊局部稳定性的定理：

定理2 在由式（10）定义的范围内，Nash均衡点E＊是系统（9）的稳定点。

需要指出的是，虽然航空公司价格调整速度αi，延迟决策权重ω对系统稳定域有显著影响，但对最终的均衡价格的结果值没有影响，也不会影响到航空公司最终的市场均衡利润。

3 数值仿真

为了更好地了解航空公司动态价格竞争系统的性质，特别是延迟决策对动态价格竞争的影响，本节将开展数值模拟仿真。设市场需求函数的参数a＝2.65，b＝1，航空公司服务单位旅客流量的成本分别为c1＝0.6，c2＝0.5，航空公司间的差异化系数分别为θ1＝0.7，θ2＝0.6，两家公司的初始市场价格为（2，3）。

3.1 延迟决策对系统稳定域的影响

由前文分析可知，航空公司价格调整速度αi和延迟决策权重ω共同构成了航空公司动态价格竞争稳定空间（α1，ω，α2），如图1所示。当αi，ω的取值在此空间内时，基于延迟决策的航空公司动态价格竞争最终将稳定于Nash均衡点E＊。

图2描述的是稳定空间（α1，ω，α2）在平面（α1，ω）上的投影。从图2中可以看出航空公司A1的稳定域范围。由于航空公司A1引入了延迟决策机制，延迟决策的权重ω对其价格调整速度α1有显著的影响。当ω的取值由1逐步递减时（即往期的决策信息比重越来越大），α1的取值范围先变大再变小，可见延迟决策并不一定能扩大稳定域［16－17］。当ω＝0.75时，α1取得最大值0.822 5。

这一结论说明：1）由于采取了延迟决策机制，航空公司A1能够获取更多的决策信息，使得其α1的变动范围增大，有助于扩大其稳定域。从图2可知，当延迟决策权重ω∈（0.5，1）时，航空公司A1的稳定域明显大于其未采用延迟决策的稳定域（即ω＝1时）。2）当ω∈［0，0.5）时，航空公司A1的稳定域将小于其未采用延迟决策的稳定域。这表明往期的决策信息所占比重越大对系统稳定性越不利，这主要因为往期的决策信息反映的是过去的历史信息，未能有效涵盖当前的市场动态，使得决策不能及时吸纳最新的当期决策信息。这也提示我们虽然引入延迟决策机制能够使得航空公司获得更多的决策信息，但需要科学确定延迟决策的权重，以确保延迟决策发挥正向积极效用。

3.2 基于延迟决策的航空公司动态价格竞争演化

图3描绘的是当系统参数取上述初始值，航空公司A1的价格调整速度α1＝1，权重ω＝0.95时，航空公司动态价格竞争随航空公司A2价格调整速度α2变化的动态演化图。从图3中可以看出，当系统参数取值满足稳定条件时，两家航空公司的价格趋于Nash均衡解。随着α2取值的增大，系统由初期稳定的均衡状态逐步进入到分岔和混沌状态。当系统进入到分岔和混沌状态后，航空公司间的市场价格波动很大，很难找出价格变化的简单规律，这给航空公司的未来价格决策带来了困难。

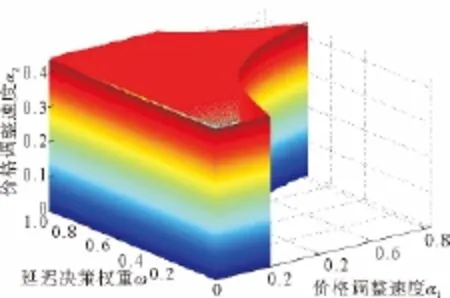
图1 系统稳定域的示意图Fig.1 Diagram of systems stable region

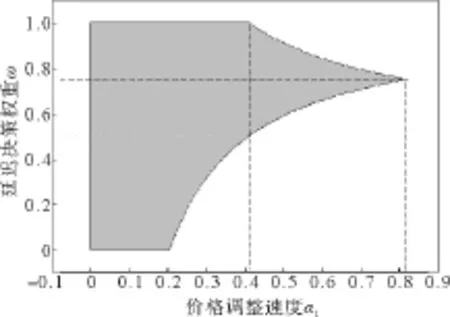
图2 系统稳定域的投影图Fig.2 Projection diagram of systems stable region

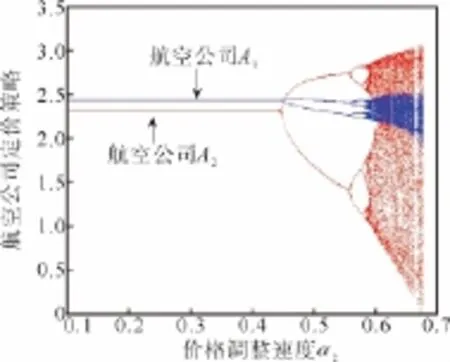
图3 基于延迟决策的航空公司动态价格竞争演化图Fig.3 Bifurcation diagram of airlines′dynamic price competition based on delayed dicision

3.3 延迟决策对航空公司竞争的累积利润的影响

图4a描绘的是当α2＝0.4（即系统处于稳定状态），其他系统参数取图3值，竞争周期为20期时的航空公司累积利润随权重ω的变化情况。从图4a中可以看出，随着ω的减小，航空公司A1的累积利润持续降低，而航空公司A2的累积利润不断增加。可见当系统处于稳定状态时，航空公司A1为引入延迟决策需要付出累积利润减少的代价，而航空公司A2却能从中获得“渔翁之利”。

图4b，4c分别描绘的是当α2＝0.5，0.6（系统处于分岔和混沌状态）时航空公司累积利润随权重ω的变化情况。从图4b和4c中可以看出：1）当系统处于分岔状态时，航空公司A1和A2的累积利润随着ω的减小均呈现先增加再减少的变化趋势。这表明航空公司A1引入延迟决策机制后，当权重ω较大（即当期决策信息所占比重较大）时，两家航空公司均能够从延迟决策机制中获益。2）当系统处于混沌状态时，航空公司A1和A2的累积利润随着ω的减小而呈波动变化，其中A1的累积利润总体呈水平波动，而A2的累积利润总体呈上升趋势。这表明航空公司A1引入延迟决策机制后，A2能够从中获得更多收益。

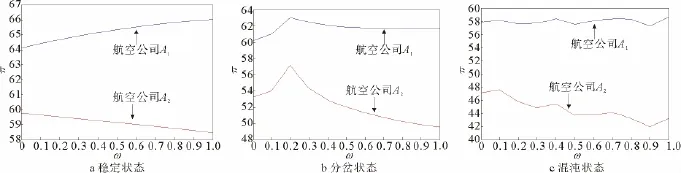
图4 不同状态下延迟决策对累积利润的影响示意图Fig.4 Influence diagrams of delayed decision on the accumulated profits under different states

综上可见，当系统处于不稳定状态时，引入延迟决策机制对航空公司竞争的累积利润有益，特别是当权重ω取值较大时，航空公司获益情况更加明显。而当系统处于稳定状态时，航空公司A1引入延迟决策机制可以有效扩大稳定域但也付出累积利润减少的代价，A2却能从中“搭便车”获取额外收益。

3.4 延迟决策对竞争到达均衡的时间的影响

由于航空公司决策不具有完全理性，因而它们的价格竞争不可能通过一次博弈就实现市场均衡，而是需要经过多轮博弈进而达到均衡状态。下面分析当系统（9）处于稳定状态时，延迟决策权重ω对竞争到达均衡的时间（即市场博弈周期数）的影响，本文假定当｜pi（t）－p＊1（t）｜≤0.000 01时市场竞争达到均衡。

图5描绘的是当系统参数取图4a值时，航空公司动态价格竞争达到均衡的时间随权重ω变化的演化图。从图5中可看出，随着ω的增大，达到均衡的时间先缩短再延长；当ω取值较大（如ω≥0.6）时，到达均衡的时间明显快于ω取值较小时，这也说明当期决策信息较往期决策信息对缩短到达均衡的时间更有利。特别地，当ω＝0.811时，航空公司动态价格竞争达到均衡的时间最短，仅需27次博弈即实现了市场均衡。

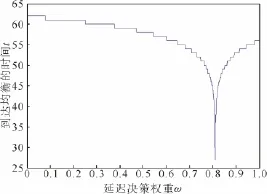
图5 延迟决策对竞争到达均衡的时间的影响图Fig.5 Influence diagram of delayed decision on the time when competition reaches equilibrium

4 结论

本文综合运用延迟决策与非线性动力学的分支理论，构建了基于延迟决策的航空公司动态价格竞争模型，分析了竞争模型均衡点的存在性与稳定性，并通过数值仿真，模拟了不同系统参数下的航空公司动态定价行为，深入分析了延迟决策对动态价格竞争模型复杂性的影响。

研究表明：1）引入延迟决策的有限理性航空公司开展动态价格竞争时，其延迟决策权重、价格调整速度等参数对竞争模型的稳定性有显著影响，一旦参数取值超过某一临界值，系统将表现出分岔、混沌等复杂的动力学现象。2）延迟决策权重对系统稳定域大小有显著影响。权重取值较大时有利于扩大系统的稳定域。3）延迟决策对航空公司累积利润有显著影响。系统处于不稳定状态时，航空公司引入延迟决策机制更有利。同时，也会出现竞争对手“搭便车”而获取额外利润的现象。4）延迟决策对竞争达到均衡的时间有显著影响。当权重取值较大时到达均衡的时间明显较快。5）决策信息（包含当期及往期）对航空公司动态价格竞争模型有重要影响。一般而言，当期决策信息对航空公司决策更有益。引入延迟决策机制的航空公司决策关键在于确定权重的取值，以有效平衡稳定域、累积利润、均衡时间等因素。

当然，本文仅从理论上研究了延迟决策对航空公司动态价格竞争复杂性的影响，对现实市场的实证分析有待进一步研究。此外，对于多方引入延迟决策机制、何时引入延迟决策机制等问题将在今后的工作中予以研究。

［1］ Gallego G，Hu M.Finite horizon dynamic pricing of perishable assets under competition［C］／／6th Annual Conference of the Revenue Management and Pricing Informs Section.New York，2006.

［2］ 高强，朱金福，蓝伯雄.国内航空公司实施收益管理的博弈分析［J］.科研管理，2006，27（6）：125－129.Gao Qiang，Zhu Jinfu，Lan Boxiong.Research of application of revenue management in civil airline［J］.Science Research Management，2006，27（6）：125－129.

［3］ 景崇毅，孙宏，曾文水.机票价格管制问题的博弈分析及解释［J］.中国软科学，2008，23（3）：140－147.Jing Chongyi，Sun Hong，Zeng Wenshui.Game theory analysis and explanation of air ticket price control problem［J］.China Soft Science，2008，23（3）：140－147.

［4］ 梅虎，朱金福，汪侠.基于博弈分析的航空收益管理定价研究［J］.预测，2006，25（6）：45－49.Mei Hu，Zhu Jinfu，Wang Xia.Research on Revenue Management Pricing of Airlines Based on Game Theory［J］.Forecasting，2006，25（6）：45－49.

［5］ Mantin B，Koo B.Dynamic price dispersion in airline markets［J］.Transportation Research Part E，2009，45（6）：1020－1029.

［6］ 王锐兰.航空公司价格竞争的博弈解释［J］.技术经济与管理研究，2004，23（3）：81－82.Wang Ruilan.Game theory analysis of airline price competition［J］.Techno economics ＆ Management Research，2004，23（3）：81－82.

［7］ Martin J C，Concepcion Roman.Hub location in the South－Atlantic airline market：a spatial competition［J］.Transportation Research Part A，2003，37（10）：865－888.

［8］ 肖艳颖.航空公司市场竞争定价博弈模型［J］.中国民航大学学报，2008，26（6）：52－55.Xiao Yanying.Game theory model of dual oligopoly airlines competition pricing［J］.Journal of Civil Aviation University of China，2008，26（6）：52－55.

［9］ Forbes S J.The effect of air traffic delays on airline prices［J］.International Journal of Industrial Organization，2008，26（4）：1218－1232.

［10］Aguirregabiria V，Ho Chun－Yu.A dynamic game of airline network competition：hub－and－spoke networks and entry deterrence［J］.International Journal of Industrial Organization，2010，28（4）：377－382.

［11］Aguirregabiria V，Ho Chun－Yu.A dynamic oligopoly game of the US airline industry：estimation and policy experiments［J］.Journal of Econometrics，2012，168（1）：156－173.

［12］Zhang Y H，Round D.Price wars and price collusion in China′s airline markets［J］.International Journal of Industrial Organization，2011，29（4）：361－372.

［13］Hu R，Xia H SH，Jiang Y.Complex dynamics for Airlines′price competition with differentiation strategy［J］.Journal of Transportation Systems Engineering and Information Technology，2013，13（1）：11－16.

［14］胡荣，夏洪山.航空公司动态价格竞争复杂性及混沌控制——基于不同竞争战略与不同理性的分析［J］.系统工程理论与实践，2013，33（1）：151－158.Hu Rong，Xia Hongshan.Complexity analysis and chaos control of airlines′dynamic price competition：an application of different competition strategies and heterogeneous players［J］.Systems Engineering－Theory ＆Practice，2013，33（1）：151－158.

［15］Agiza H N，Elsadany A A.Nonlinear dynamics in the Cournot duopoly game with heterogeneous players［J］.Physica A，2003，320（15）：512－524.

［16］Yassen M T，Agiza H N.Analysis of a duopoly game with delayed bounded rationality［J］.Applied Mathematics and Computation，2003，138（2）：387－402.

［17］徐峰，盛昭瀚，姚洪兴，等.延迟决策对一类双寡头广告博弈模型的影响分析［J］.管理科学学报，2007，10（5）：1－10.Xu Feng，Sheng Zhaohan，Yao Hongxing，et al.Study on a duopoly advertising model with delayed decisions［J］.Journal of Management Science in China，2007，10（5）：1－10.