基于盲源分离的电站锅炉多源泄漏定位研究

安连锁，冯 强，沈国清，张世平，王 鹏

(华北电力大学电站设备状态监测与控制教育部重点实验室，北京102206)

0 引言

锅炉压力管道泄漏对电站安全经济运行产生严重的影响，当泄漏至一定程度时往往采取被迫停炉检修，若能够对泄漏点进行精确定位，可以及时恢复生产，减小损失。然而以往的泄漏检测定位技术建立在单源泄漏的基础上［1-3］，在检测多源泄漏时容易产生虚假泄漏点，导致停炉检修工作量显著增加。

本文对多源泄漏问题中的混叠信号分离问题进行研究，提出基于盲源分离的电站锅炉多源泄漏定位方法，并结合实测喷流信号进行仿真研究。该方法主要通过盲源分离对多源泄漏信号进行分离，获得多个源信号，然后针对各源信号进行时延估计并定位。

1 多源泄漏信号盲源分离

盲源分离［4-5］，是指将采集到的混合信号进行分离恢复出若干未知源信号的方法。盲信号分离中，传感器采集的信号中源信号未知，混合方式也未知。在电站锅炉多源泄漏中，声感知设备采集到的泄漏信号包含多个泄漏源，对于非高强声而言，源信号之间的混合方式为线性关系。

将噪声作为采集信号中的一个独立源信号进行讨论［6］，则线性瞬时混合模型［7-8］为

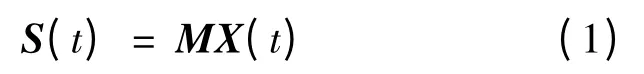
式中:M 为m × n 维混合方式矩阵，矩阵中每个元素表示一个混合系数，(X(t)=［x1(t)，x2(t)，…，xn(t)］T表示独立源信号矢量组合。

若分离后的源信号记作y(t)，则

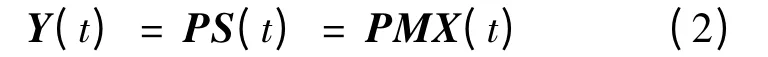
式中:Y(t)=［y1(t)，y2(t)，…，yn(t)］T表示源信号的估计信号;P 表示解混矩阵，令W = PM，那么Y(t)= WX(t)。

上述模型建立在噪声与源信号具有相互统计独立的前提下。

对于非欠定情况下，即声感知设备个数不小于源信号个数(m ＞n)，因此混合矩阵M 为满秩矩阵，存在逆矩阵M-1 。由于缺少源信号和混合方式等先验信息，在利用采集信号S(t)恢复源信号时，需要求解解混矩阵P。

独立分量分析(Independent Component Analysis，ICA)［9］作为一种经典的盲源分离算法，能够有效的分离盲源信号，被广泛应用于故障诊断、语音信号分离、生物医学信号处理等领域。该算法通过各源信号之间的统计独立性对采集信号进行估计，采用建立目标函数最值求解的方式实现源信号分离。芬兰学者于1999年提出固定点算法(FastICA)，实现了盲信号快速分离，提高了信号分离的实时性。进行FastICA 之前首先对信号进行去均值及白化处理。白化处理的优点为可以去除信号间各分量的相关性，使其二阶统计独立。采用协方差矩阵特征值分解的方法进行白化处理［10］:

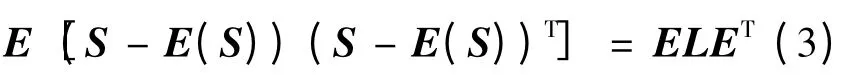
式中:L 表示特征值对角矩阵;E 表示与L 对应的特征向量矩阵，则白化向量可表示为

选取峭度度量信号的非高斯性，那么y 的峭度为

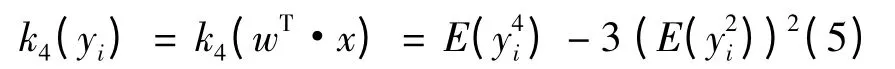
式中:yi表示Y 的第i 个分量;k4(yi)表示yi的四阶累积量。

FastICA 的迭代过程为［10］:

(1)对初始量w1(0)赋值，条件‖wi(0)‖ =1，更新k = 1 ;

(2)根据wi(k + 1)= E［xi(wi(k)Txi)3］－3wi(k)对wi(k)进行更新;

(4)对wi(k +1)进行正交化处理，wi(k +1);

2 多源泄漏定位

现有的声源定位技术有波束成形、谱估计和到达时延定位技术。到达时延定位技术由于其计算量小、精度高等优点被广泛应用于麦克风定位、通信及军事等领域。到达时延定位分为两个主要部分:首先将分离出的源信号分别进行时延估计，然后通过定位算法得出泄漏点三维坐标。

2.1 广义互相关时延估计

互相关算法［11］是描述两空间独立信号时域上相关性的基本方法。基于广义互相关算法的时延估计主要通过两个相互独立的声感知设备采集信号为基础，对采集信号进行互相关运算，互相关函数的最大峰值对应时延即为泄漏源至两声感知设备的到达时延差。

假设经盲源分离后所得由同一泄漏源发出的不同空间位置的采集信号数学模型为

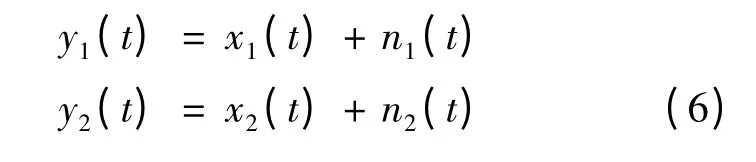
式中:y(t)表示分离出的泄漏源估计信号;x(t)表示泄漏源信号;n(t)表示噪声信号。

则由同一泄漏源发出的不同空间位置的两采集信号的广义互相关函数R12(τ)为

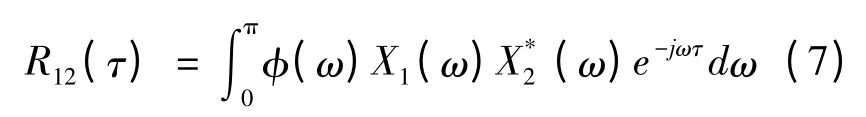
式中:φ(ω)为权函数;τ 为时延估计;X 为傅里叶变换;* 表示复共轭。

在此选取相位变换(PHAT)加权作为权函数，其表达式为

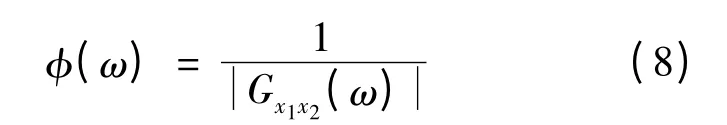
2.2 LS 定位算法

最小二乘法(Least Squares，LS)算法［12］是一种基于均方误差最小的无偏估计方法，不需要先验信息，且计算过程简单，应用较为广泛。

将声感知设备进行坐标标记，表示为(xi，yi，zi)，(i =1，2，…，N)，其中将r1= (x1，y1，z1)标记为基准点，多源泄漏中的某一泄漏源记作rsj=(xsj，ysj，zsj)，下标j 表示第j 个泄漏源。

定义某一泄漏源到各声感知设备的距离为

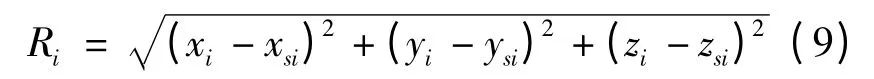
令Ri1= Ri－ R1，那么由可得

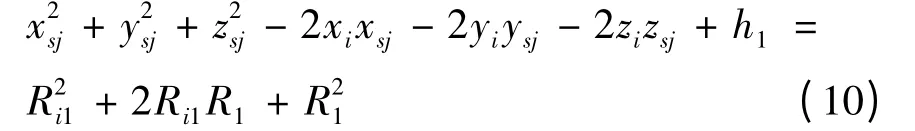
将式(9)等号两侧同时平方，并取i = 1，得

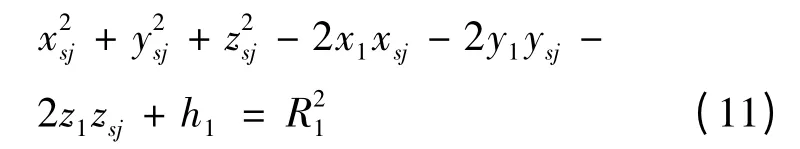
式(10)与(9)相减得

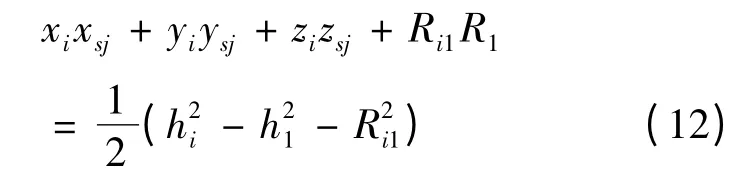
由式(12)可得

式中:

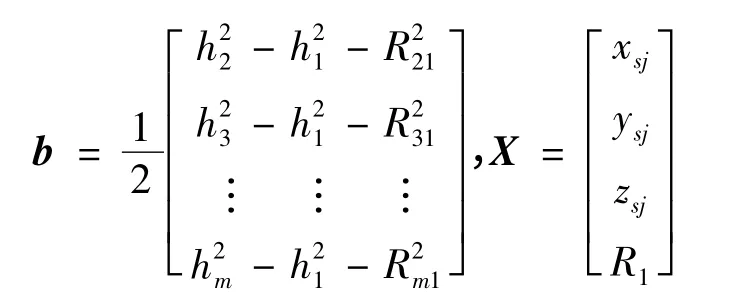
利用最小二乘法解方程(13)得到某一泄漏源坐标估计:

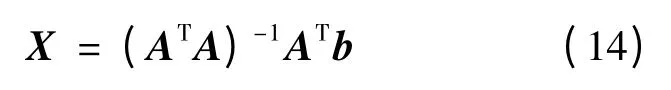
3 电站锅炉多源泄漏定位仿真研究

为验证算法性能，分别对盲源分离及多源泄漏定位进行评估。盲源分离仿真研究中选择1～8 000 Hz线性扫频信号、0.8 MPa 压力5 mm 及8 mm口径喷流喷流信号作为信号源。

3.1 盲源分离性能评估

为了能从时域图上直观分析盲源分离的性能，选取扫频信号与8 mm 口径0.8 MPa 压力喷流信号进行两种随机方式线性叠加，针对随机叠加后的两信号进行盲源分离，对比源信号与估计信号，可得盲源分离能够对两混叠信号进行有效的分离，如图1～2所示。

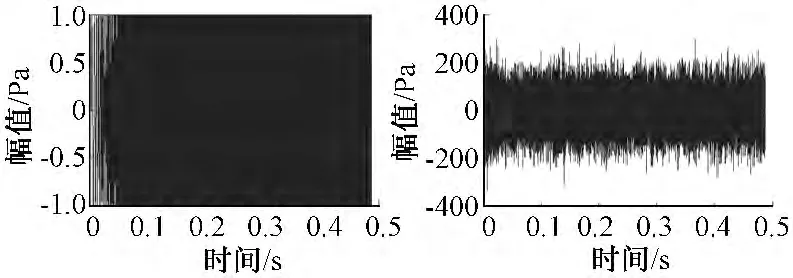
图1 源信号Fig.1 Source signal

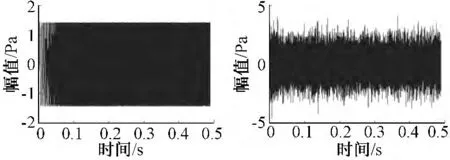
图2 分离所得信号Fig.2 Separation of the mixing signal

Fastica 算法的一个缺点即为分离信号的幅值不确定性［13］，然而在多源泄漏泄漏定位中，注重信号分离后的时延成分，幅值大小并不造成实际影响。分别对扫频信号、喷流信号人为给定9.765 ms、4.883 ms 时延值，将无时延的扫频信号与喷流信号进行两组随机混合获得位置一信号，同时将含时延值的扫频信号与喷流信号进行两组随机混合获得位置二信号。

位置一信号通过盲源分离获得两估计信号，分别同位置二两估计信号进行互相关，根据广义互相关算法原理，具有相关性的信号能够得到明显的峰值，而不相关信号无明显峰值。从图3(a)、(b)可以看出，不同位置分离所得扫频信号与位置二所得扫频信号具有相关性，时延值为9.756 ms 与真实值相差0.009 ms，该误差可以忽略不计;位置一分离所得喷流信号与位置二所得喷流信号具有相关性，时延值为4.883 ms，与实际值相同。同时两位置分离所得扫频信号与喷流信号不具有相关性，如图3(c)、(d)所示。

图3 不同位置分离信号相关分析Fig.3 Correlation analysis of separation source with different positions

在实际多源泄漏定位中，由于信号均为喷流信号，无法从分离后的时域图区别哪个估计信号对应哪个泄漏源，因此采用上述同样方式将不同口径的喷流信号进行随机混合，以5 mm 口径和8 mm口径为例进行仿真研究。

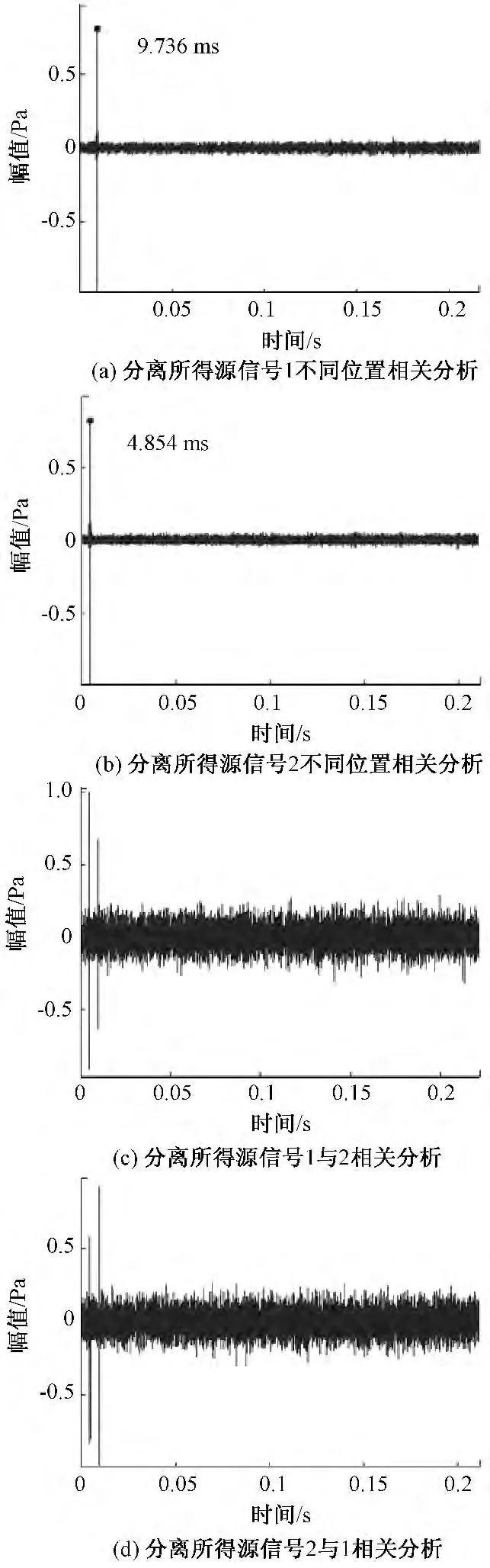
图4 不同位置分离信号相关分析Fig.4 Correlation analysis of separation source with different positions

如图4(a)、(b)所示，通过相关分析可得，对于同一泄漏源，具有明显的单峰值，峰值所在x 坐标即为时延值，5 mm 口径喷流信号所得时延值为9.736 ms，与真实值相差0.029 ms，8 mm 口径喷流信号所得时延值为4.854 ms，与真实值相差0.029 ms，时延估计精度保持在工程误差范围内。同时不同位置分离所得的不同口径喷流信号具有弱相关(不同泄漏源相关函数峰值与上包络线均值比小于同一泄漏源对应值)，且存在明显的双峰值，如图4(c)、(d)所示。因此在实际运用中可以通过将不同位置分离后所得信号分别进行互相关分析，通过信号的相关性区别是否来自同一泄漏源，进而可以有效克服盲源分离排序不确定性的缺点。

3.2 定位精度分析

以国内300 MW 机组为模型，选择水冷壁空间某段区域尺寸，模型结构为:长10 m，宽10 m，高5 m。声感知设备分别布置在该区段内不同的8 个位置，其中每个位置分布多个声感知设备用于该位置盲源分离。多源泄漏定位首先通过盲源分离得到不同泄漏源，然后针对各泄漏源分别进行定位，为简便起见，对于定位精度的分析采用单源泄漏定位模型。避免水冷壁区域壁面泄漏的特异性，对整个模型空间进行适普性模拟，因此选择泄漏点为S(2，4，4)，声波传播速度约为757 m/s，时延误差范围为-0.15 ms 至0.15 ms，如图5所示。

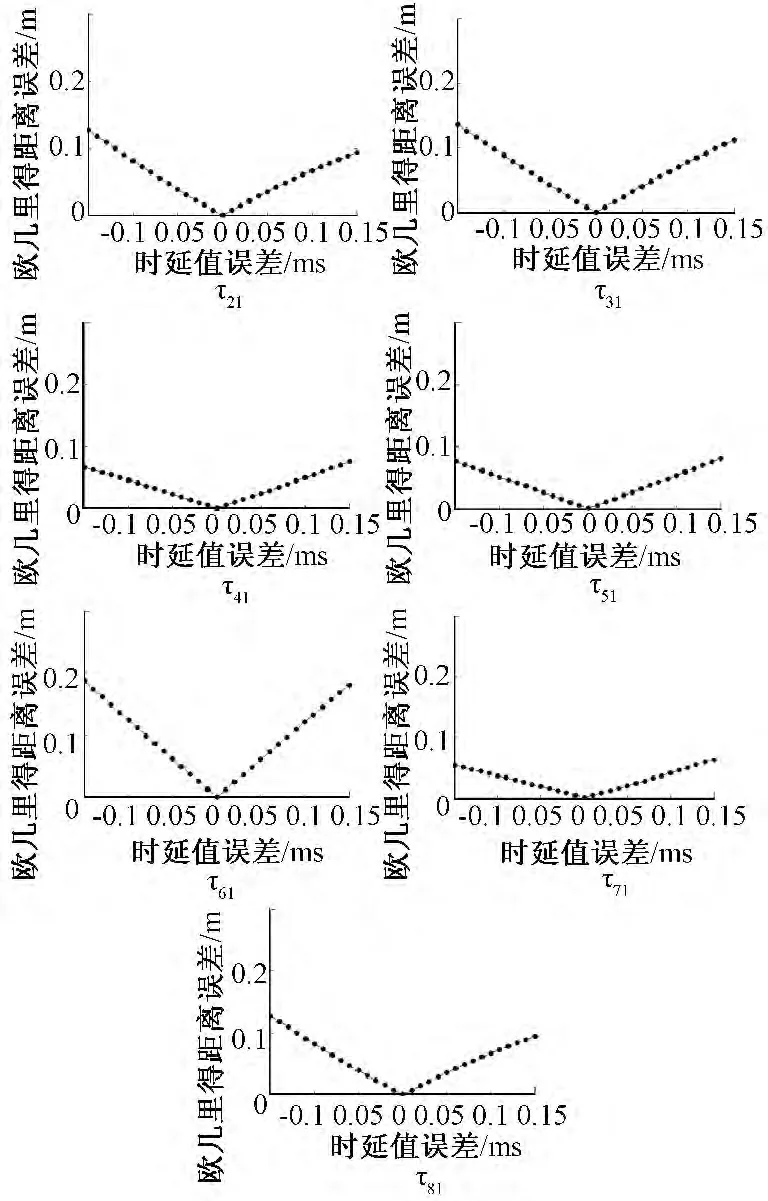
图5 不同通道时延误差对精度的影响Fig.5 Influence on location accuracy with TDOA errors in different channels

由图 5 可知，LS 定位算法时延误差在-0.15 ms至0.15 ms 范围内时，在时延误差最大处，对应欧几里得距离误差最大，最大误差保持在0.2 m 以内，相对于模型尺寸，该误差在2%以内，满足工程精度需求。

4 结论

(1)盲源分离能够将有效的将频段混叠多源泄漏信号进行分离，且不同位置分离所得来自同一泄漏源的估计信号仍然保持较好的相关性，能够准确的反应泄漏源至不同位置声感知设备的时延值。分离后估计信号时延值与实际时延值误差保持在工程精度范围内。

(2)含时延误差的LS 算法定位精度保持在工程精度范围内，且无需迭代过程，计算方法简单，处理速度快，适用于在线检测。

(3)通过仿真研究，基于盲源分离的电站锅炉多源泄漏定位方法在理论上是可行的，为电站锅炉多源泄漏定位实际工程应用提供了参考。

［1］安连锁，王鹏，姜根山，等.锅炉承压管泄漏双曲面定位的遗传算法优化［J］.中国电机工程学报，2010，30 (26):17-22.

［2］安连锁，王鹏，姜根山，等.锅炉承压管泄漏声传播时间延迟估计［J］.中国电机工程学报，2012，32(2):16-23.

［3］王振涛，郝忠孝，贺洪江.基于传声器阵列的声源定位系统的研究［J］.华北电力大学学报，2009，36 (5):103-105，112.

［4］张洁，高宏力，陈春俊，等.高速列车非平稳振动信号盲源分离方法及应用［J］.机械工程学报，2014，50 (19):97-104.

［5］Swartling M，Sällberg B，Grbic′ N.Source localization for multiple speech sources using low complexity nonparametric source separation and clustering［J］.Signal Processing，2011，91 (8):1781-1788.

［6］苏永振，袁慎芳.基于独立分量分析的多源冲击定位方法［J］.振动与冲击，2009，28 (8):134-137，157.

［7］滕鹏晓，章林柯，陈日林，等.基于双传声器对的多声源二维定位跟踪算法［J］.声学学报，2010，35(2):230-234.

［8］Buchner H，Aichner R，Stenglein J，et al.Simultaneous localization of multiple sound sources using blind adaptive mimo filtering［C］.2005 IEEE International Conference on Acoustics，Speech，and Signal Processing，Philadelphia，PA，USA，18-23 May，2005:97-100.

［9］Hyvarinen A，Oja E.Independent component analysis:algorithms and applications［J］.Neural Networks，2000，13 (4-5):411-430.

［10］郑慧峰，吕江明，张斌，等.基于FastICA 的超声A波信号降噪研究［J］.中国机械工程，2012，23(10):1135-1139.

［11］安连锁，张世平，李庚生，等.电站锅炉声学测温中时延估计试验研究［J］.动力工程学报，2012，32(3):197-203.

［12］康玉梅，刘建坡，李海滨，等.一类基于最小二乘法的声发射源组合定位算法_康玉梅［J］.东北大学学报(自然科学版)，2010，31 (11):1648-1651，1656.

［13］吕淑平，方兴杰，杨丽微.独立分量分析的算法分析与改进［J］.噪声与振动控制，2013，33 (6):153-157.