压缩空气储能填充床储热特性研究

姜 萍，赵振家

(1.河北大学电子信息工程学院，河北保定 071000;2.河北大学罗克韦尔自动化实验室，河北保定 071000)

0 引言

在我国当前阶段，能源需求不断增长难以满足工业生产，大力发展可再生能源是转变能源消费观念，发展低碳经济的必由之路。太阳能和风能以分布广泛，取材丰富因而作为可再生能源开发的重点。但是风能和太阳能分布不均匀，受到时间和地区的限制，并且风能和太阳能具有间歇性和随机性，因而不能够为生产提供稳定的能量输出。为此人们提出如果能够把风能和太阳能存储起来，便能够改善风光天然的间歇性和随机性，从而能够提高电能品质，保证用电的可靠性，为生产生活提供稳定的能量输出。储能技术便成为了当今研究的焦点，发展储能技术能够有效地解决能源需求和能源供应之间的矛盾。

压缩空气储能系统是一种能够实现大容量和长时间电能存储的电力储能系统，在峰谷电能回收调节、平衡负荷、频率调制、分布式储能等方面具有很大应用潜力。利用电网低谷或可再生能源供给过剩电能带动压缩机，通过压缩空气储存多余的电能。在用电高峰期或可再生能源供给不足时，高压气体经过填充床温度升高，高温高压气体通过膨胀机做功发电。压缩空气储能系统的原理图如图1所示。储热技术是有效提高压缩空气储能效率的重要方式，从而既拥有远高于压缩空气储能的能量密度，又大大提高空气储能的效率。蓄热的主要方式分为3 种:显热蓄热、潜热蓄热、和化学反应蓄热，填充床是最常见的显热蓄热。显热蓄热的运行方式简单，成本低，热效率高，因此适合大规模应用。

文献［1］分析了以岩石，钢球和相变硝酸盐作为储热材料时的出热量、热分层、相间温差等特性以及储热—释热周期对热效率的影响，表明填充床是解决可再生能源储热问题的储热方式。文献［2～3］开展了不同压力下填充床蓄热周期实验，测量了填充床内温度分布和进、出口空气温度随时间的变化，实验表明提高罐壁保温性能，以较大空气质量流量和较低空气压力条件下可以得到较高的蓄热效率。文献［4～5］为了提高压缩空气储能系统效率建立了基于涡旋压缩机的压缩空气储能系统的动态模型，为适应控制策略的研究，建立了兼顾过/欠膨胀机损耗的涡旋膨胀机平均模型。文献［6］提出了一种模型自激式发电机，仿真实验通过连续不断的压缩空气放电来驱动感应发电机，表明此设备可以为可再生能源直接连接电网供电。文献［7～8］将压缩空气储能系统与风力发电厂相结合进行了讨论研究，表明压缩空气储能系统能够有效改善风力发电厂输出功率的稳定性，起到了削峰填谷的作用。文献［9～10］在MATLAB/SIMULINK 中讨论了压缩空气储能系统的动态建模问题，给出了压缩机，储气室和膨胀机的数学模型，设计了电网侧的控制系统，建立了电力电子装置调节气动马达转子的转速进行充放电。文献［11］在流体动力学基础上建立的压缩空气储能系统仿真模型进行了热力分析。但是对于带有蓄热装置的压缩空气储能系统的建模和热力学分析工作鲜有报道，与传统压缩空气储能系统相比，带有蓄热装置的压缩空气储能系统不依赖于化石燃料且无污染，可以大规模推广。

本文采用MATLAB 数值计算方法求解了传热模型的偏微分方程，得到了模型的数值解和模拟图形，并基于ANSYS FLUENT 14.0 对石子填充床内的流体动力学和传热特性进行了仿真，对空气通过填充床的储热过程进行了数值模拟，通过计算得到了填充床出口温度与入口空气质量流量的传递函数，实验结果表明计算所得的传递函数能够完整表述填充床储热动态特性。

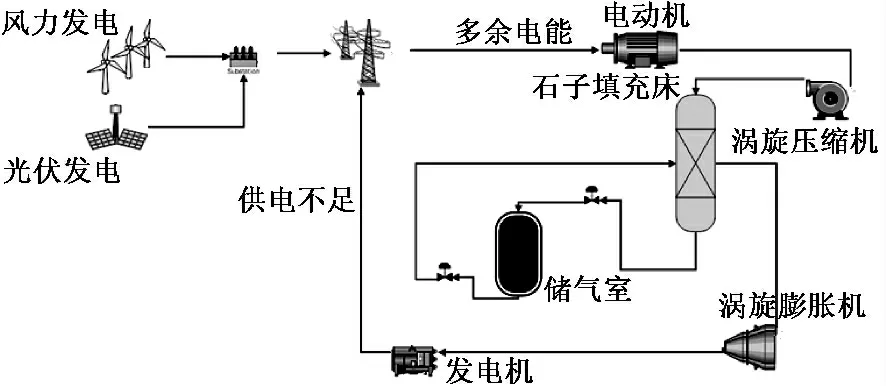
图1 压缩空气储能原理图Fig.1 Schematic diagram of compressed air energy storage

1 基于一维非稳态导热－扩散传热模型的验证

Schumann 最早通过数学推导得到了填充床内流体温度与实践距离的关系，Littman 和Gunn 发现在低雷诺数下流体和固体之间的扩散现象明显，因而采用了一维非稳态导热扩散两相模型来描述填充床内的传热现象。

经过压缩机和膨胀机后的空气为高温高压气体，换热介质为多孔介质。考虑空气与颗粒之间的温差，在假设流体速度分布均匀，填充床为绝热系统，孔隙率均匀，气体与固体的物性参数不随温度变化，固相与流体相具有连续性，忽略热辐射和自然对流，并且固体颗粒和流体无径向温度梯度的情况下，Kunii 和Smith 通过数学推导得到理想填充床内流体及固体温度与时间和距离的函数关系式，建立了流动方向上固体与流体的一维、非稳态和常物性能量微分方程，式(1)为流体相方程，式(2)为固体相方程。

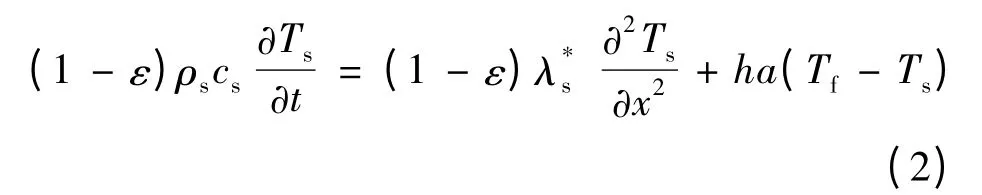
式中:Ts和Tf分别为填充床内石子和空气温度;x为沿流体流动方向距离;t 为时间;cs和cf分别为石子和空气比热;ε 为孔隙率;mf为单位截面空气质量流量;a 为单位体积填充床内石子总面积;h为空气与颗粒之间的传热系数。和分别为石子和空气的导热系数。取ε =0.4，ρs=2 650 kg/m3，cs=0.92 kJ/(kg℃)，h =2w/(m·k)，a =0.001 m3，L =1.5 m，mf=0.05kg/s，ρf=17 kg/=4 w/(m·k)，带入偏微分方程整理得

初始条件和边界条件为

Tf(0，t)= 430(K)Ts(x，0)= 298(K)

对于偏微分方程的某些定解问题不能通过解析解严格求出，只能用近似方法来求出满足实际需要的近似解，即它的数值解。偏微分方程的数值解法主要有有限差分法、有限元法以及边界元法等。本文采用MATLAB 中的pdepe 函数来求解偏微分方程。

MATLAB 中的pdepe 函数可以求解一般的PDEs，具有较大的通用性，pdepe 函数的调用格式为sol=pde(m，@ pdefun，@ pdeic，@ pdebc，x，t)，@pdefun 是问题的描述函数，@pdeic 是PDE 的初值条件，@ pdebc 是PDE 的边界条件描述函数。输出参数sol:是一个三维数组，sol(:，:，i)表示ui的解，通过sol，就可以使用pdeval()计算某个点的函数值。带入数值后得到固体和流体温度与时间和流体流动方向距离关系如图2、3所示。

2 基于ANSYS 填充床储热特性仿真

计算流体力学是近代流体动力学的一个重要分支，FLUENT 是国际知名的CFD 软件，集成了非常丰富的参数化方案和物理模型，可用于多种流体问题的数值模拟。由于FLUENT 稳定性能好，运算精度高，适用范围广，高效省时，有先进的动/变形网格技术和强大的网格支持能力而备受人们亲睐。

图2 固体温度与时间和流体流动方向距离关系图Fig.2 The diagram of the solid temperature for time and the fluid flow direction distance

图3 流体温度与时间和流体流动方向距离关系图Fig.3 The diagram of the fluid temperature for time and the fluid flow direction distance

填充床是内部还有众多空隙的多孔介质，蓄热的主要方式分为3 种:显热蓄热、潜热蓄热、和化学反应蓄热。本文选择具有显热储热特性的球形石子颗粒为内部填充满材料，填充床进口管道直径为159 mm，高为1 500 mm，球形石子颗粒粒径为10 mm，石子填充区域直径为500 mm，高度为1 200 mm。本文利用ANSYS FLUENT14.0 对填充床的储热特性进行了仿真研究，为了降低数值模拟的复杂度并缩短计算时间，假设填充床与环境绝热，不考虑援助罐体热容的影响，填充床内孔隙率分布均匀，忽略热辐射的影响。

本文利用FLUENT 前处理软件Gambit 进行网格的划分，读入并检查网络之后，设置求解器参数，湍流模型中选择k－ epsilon(2eqn)，定义材料属性，设置材料为岩石，导热系数为2 W/(m·K)，密度为2 650 kg/m3;设置区域条件，孔隙率为0.4;设置边界条件，对空气进口边界条件进行设置，本实验系统所采用填充床入口直径为6 cm，所用压缩机的压缩比约为1.44，空气入口质量流量为0.05 kg/s，入口空气温度为430 K，填充床为绝热边界;最后进行求解计算，设置求解松弛因子和收敛临界值，设置流场初始化，用Patch 按钮对填充床的初始温度进行设置，填充床内石子和壁面初始温度为298 K，监视出口温度的变化曲线，得到出口温度曲线如图4所示。

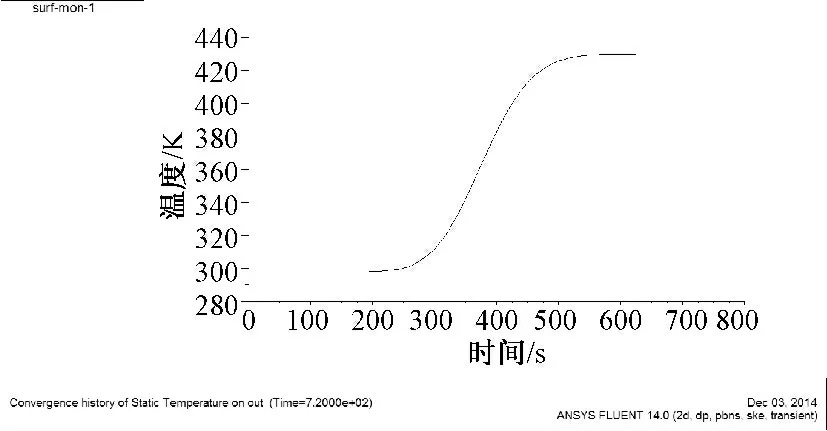
图4 空气出口温度与时间的关系Fig.4 The relationship between outlet temperature and time

由出口温度变化曲线可以看出，出口热风达到最高温度所需时间很短，由于采用的是气固换热热平衡方程，所以空气最高温度与入口空气温度相等，均为430 K，300 s 之前的时间，出口空气温度均保持为298 K，随着填充床的不断升温，出口空气温度逐渐升高，最终达到600 多秒时，换热结束，达到热平衡。表(1)显示了空气入口质量流量为0.05 kg/s，入口温度为430 K 时，出口空气温度与时间的关系。

图5～8 分别显示了当时间为300 s，350 s，400 s，500 s 时填充床的温度分布情况。

由温度场云图可以看出，填充床是自下而上逐层升温的，流动方向上温度梯度大，横向温度梯度几乎为0。

表1 填充床出口温度与时间关系表Tab.1 The relation table for outlet temperature and time of the packed bed

图5 300 s 时填充床的温度分布图Fig.5 The temperature distribution of the packed bed on 300 second

3 填充床储热特性数值分析

建立被控过程数学模型的方法包括机理法和测试法，压缩空气储能系统填充床的热力特性为复杂的偏微分方程组描述形式，不便于采用机理法建模。为了获得填充床的动态特性，通入热空气之后，得到填充床的空气出口温度呈现S 形单调曲线，本文采用阶跃响应曲线两点法来求得填充床动态特性的特征参数，得到填充床出口空气温度与入口空气质量流量之间的传递函数。

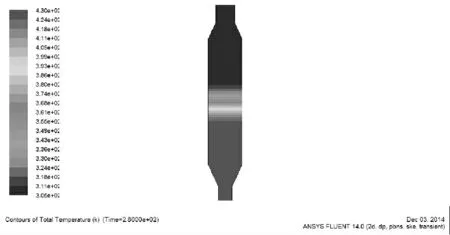
图6 350 s 时填充床的温度分布图Fig.6 The temperature distribution of the packed bed on 350 second

先将阶跃响应曲线化为无量纲的阶跃响应y*(t)，阶跃响应的稳态值y(∞)与阶跃输入的幅值x0之比为被控过程的静态放大系数，K =y(∞)/x0，K = 13.2，取y*(t1)=0.4，y*(t2)=0.8 两点，从曲线上确定对应的t1=367(s)，t2=395(s)，由t1/t2= 0.785，确定系统为16 阶，T =。

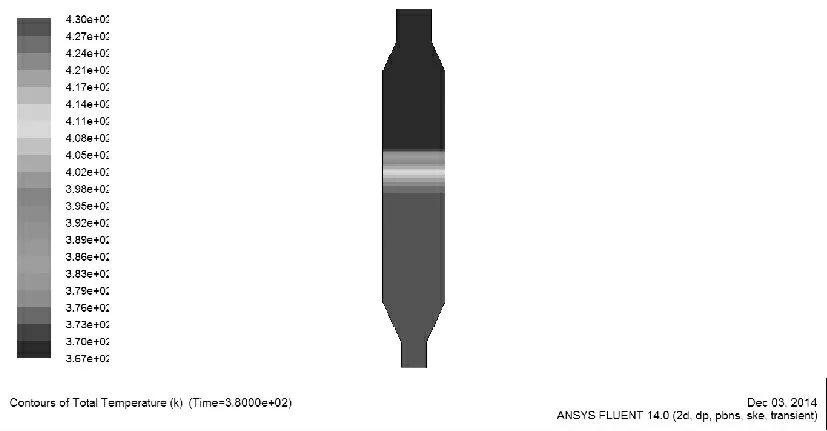
图7 400 s 时填充床的温度分布图Fig.7 The temperature distribution of the packed bed on 400 second

图8 500 s 时填充床的温度分布图Fig.8 The temperature distribution of the packed bed on 500 second

最终得到填充床的传递函数:

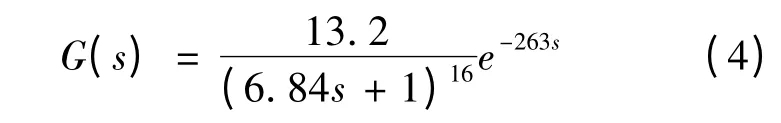
填充床在压缩过程中吸收压缩空气的热量，而在膨胀过程中填充床要对高压空气进行加热，本文得到的填充床蓄热过程的数学模型并不适用于膨胀发电填充床蓄冷过程的数学模型，膨胀过程空气出口温度的变化曲线如图9所示。

图9 膨胀发电时空气出口温度与时间的关系Fig.9 The relationship between outlet temperature and time in expansion system

经过计算得到膨胀发电过程填充床出口空气温度与入口空气质量流量的传递函数为

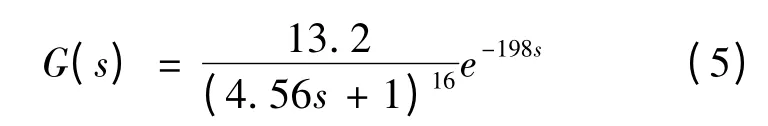
4 实验结果分析

本实验系统所采用填充床入口直径为6 cm，所用压缩机的压缩比约为1.44，空气入口质量流量为0.05 kg/s，入口空气温度为430 K，填充床内石子和壁面初始温度为298 K，岩石孔隙率为0.4，通过ANSYS FLUENT 仿真实验得到了填充床出口温度的变化曲线，并在MATLAB 中绘制了填充床边界部分固体温度的实验曲线与理论推导曲线的对比图，分析了实验所得的数据曲线与传递函数响应曲线存在差异的原因。

图10所示为填充床边界部分固体温度的实验曲线与理论推导曲线的对比图，由于计算模型较简单，而仿真所用模型相对精确，导致由理论推导所得曲线与实验的数据曲线存在一定误差，但所反映填充床边界部分固体温度变化大体一致。图11所示为实验所得的数据曲线与传递函数响应曲线的对比图，由于传递函数为有限阶函数，不能完全描述实验所得数据曲线，导致实测值偏小于传递函数值，从图中可以看出实验所得传递函数能够近似描述热空气流过填充床后空气温度的变化。

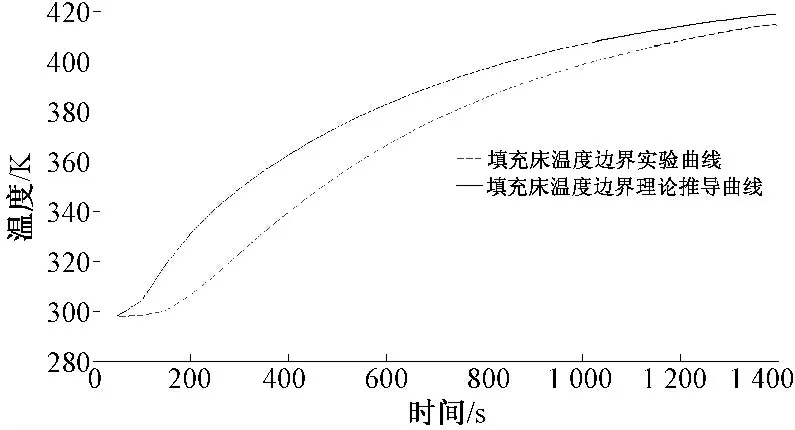
图10 填充床边界部分固体温度的实验曲线与理论推导曲线的对比图Fig.10 The comparison between the experimental curve and theoretical derivation curve for the solid temperature of boundary part

压缩空气储能系统热力特性多为复杂的偏微分方程组描述形式，难以用于控制系统的设计，本文研究了填充床的蓄冷蓄热过程中热力特性参数的动态变化，利用仿真软件模拟及数值拟合，采用测试法进行数学建模，得到了适用于控制系统设计的数学模型。

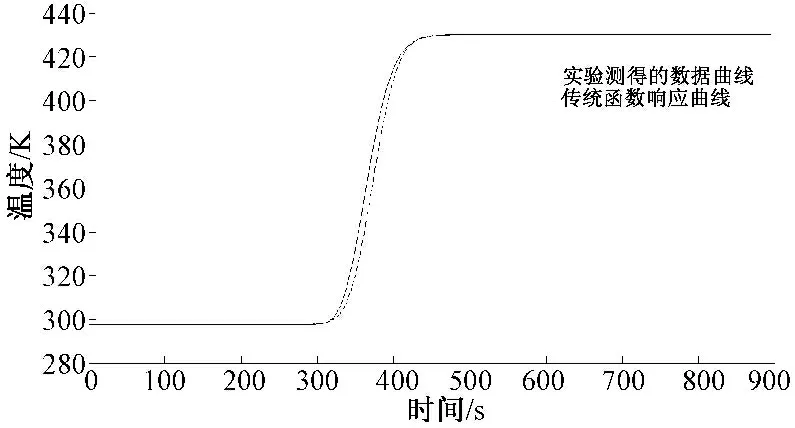
图11 实验所得的数据曲线与传递函数响应曲线的对比图Fig.11 The comparison between the experimental curve and the transfer function response curve

5 结论

与电池、超级电容、飞轮等储能方式相比，压缩空气储能是唯一可在综合效益方面和抽水蓄能相媲美的储能方式［12］。但传统压缩空气气体膨胀需要与化石燃料混合燃烧，对化石燃料和地理环境的依靠和排放污染等方面限制了大规模推广。带蓄热装置的压缩空气储能系统可以解决传统压缩空气储能系统需要补燃这一缺点，填充床蓄热的运行方式简单，成本低，热效率高，适合大规模应用。

研究非补燃式压缩空气的建模对于控制系统的设计研究具有重要意义。通过对被控过程及相关设备的数学模型进行仿真和模拟试验，在计算机上进行计算、分析，以获取代表接近真实过程的定量关系，可以为控制系统的设计和调试提供数据，从而大大降低设计实验成本并节约时间、加快设计进程。本文以石子填充床作为研究对象首先利用MATLAB 数值计算方法，求解得到了填充床一维非稳态导热－扩散两相模型相应的偏微分方程，得到了该模型的数值解和模拟图形，并基于ANSYS FLUENT 14.0 对石子填充床内的流体动力学和传热特性进行了仿真，对热空气通过填充床储热器的储热过程进行了数值模拟，通过计算得到了填充床出口温度与入口空气质量流量的传递函数。

实验结果表明，计算所得到的传递函数曲线可以完整描述实验所得曲线，并且与理论公式计算所得曲线基本吻合，具有较强的实用性，可以运用于非补燃式压缩空气储能系统的建模中。

［1］赵岩，王亮，陈海生，等.填充床显热及相变储热特性分析［J］.工程热物理学报，2012，33 (12):2052－2057.

［2］杨亮，刘佳，岳雷，等.岩石填充床蓄热性能试验研究［J］.可再生能源，2013，31 (8):88－92.

［3］刘佳，杨亮，盛勇，等.压缩空气储能的多级填充床蓄热实验研究［J］.科学技术与工程，2013，13(6):1462－1468.

［4］褚晓广，张承慧，李珂，等.基于涡旋压缩机的新型压缩空气储能系统动态建模与效率分析［J］.电工技术学报，2011，26 (7):126－132.

［5］褚晓广，张承慧，李珂，等.涡旋膨胀机发电系统效率优化控制策略［J］.电工技术学报，2012，27(6):25－31.

［6］Vongmanee V，Monyakul V.A Modeling of Self Excited Induction Generators Driven by Compressed Air Energy Based on Field Oriented Control Principle［C］.IEEE 2nd International Conference on Power and Energy，Johor Baharu，Malaysia，1－3 December，2008:834－838.

［7］Saadat M，Li P Y.Modeling and Control of a Novel Compressed Air Energy Storage System for Offshore Wind Turbine［C］.2012 American Control Conference，Montreal，QC，27－ 29 June，2012:3032－3037

［8］Dahraie M V，Najafi H R，Azizkandi R N.Study on Compressed Air Energy Storage Coupled With a Wind Farm［C］.2012 Second Iranian Conference on Renewable Energy and Distributed Generation，Tehran，Iran，6－8 March，2012:147－152.

［9］Martínez M，Molina M G，Mercado P E.Dynamic Performance of Compressed Air Energy Storage (CAES)Plant for Applications in Power Systems［C］.2010 IEEE/PES Transmission and Distribution Conference and Exposition，Latin America，Sao Paulo，8－ 10 Nov.，2010:496－503.

［10］Hasan N S，Hassan M Y，Majid M S，et al.Mathematical Model of Compressed Air Energy Storage in Smoothing 2MW Wind Turbine［C］.2012 IEEE International Power Engineering and Optimization Conference，Melaka，Malaysia，6－ 7 June，2012:339－343.

［11］Grazzini G，Milazzo A.A Thermodynamic Analysis of Multistage Adiabatic CAES［C］.Proceedings of the IEEE，2012，100 (2):461－472.

［12］卢强.浅谈压缩空气储能—专访中国科学家卢强院士［N］.中国能源报，2012－06－02.