直流复合绝缘子积污特性的数值模拟研究

吕玉坤，李国超，卫少科，杨 硕

(1.华北电力大学，河北保定071003;2.内蒙古康远工程建设监理有限责任公司，内蒙古呼和浩特010070)

0 引言

污闪是电力系统外绝缘的最大威胁，污闪事故发生的次数虽然排在第二，仅次于雷电灾害次数，但它带来的损失却是雷害的近10 倍［1］。随着我国超、特高压直流输电的发展，污秽条件下电气外绝缘问题显得更加突出。因此，防止绝缘子发生污闪是提高电力系统安全运行最为重要的手段和措施［2］。

积污是绝缘子发生污闪的前提，目前国内学者对绝缘子积污的研究主要通过人工污秽试验和自然积污实验［3-7］，而绝缘子积污特性数值模拟研究相对较少。文献［8］通过风洞试验、空气流场测试和数值模拟，分析比较了不同绝缘子的空气动力性能，未研究其积污特性。文献［9］对三种不同绝缘子的积污过程进行了模拟，并对所获得的不同风速和粒径下的积污速率进行了比较与分析，但其研究过程中将绝缘子视作不带电体，忽视了电场的作用。文献［10］利用同轴电极模型进行实验，探究了电场对颗粒运动的影响，但并未对具体的积污过程进行模拟。

复合绝缘子因其体积小、重量轻、防污闪效果好等优点，已在我国交直流输电线路中得到了广泛应用。本文以FXBW-110/120-2 型复合绝缘子为研究对象，利用多物理场耦合效果较好的Comsol 数值模拟软件［11］，对该绝缘子在直流电压下的积污特性进行模拟研究，重点分析研究风速和污秽粒径对其积污特性的影响。

1 数值模拟的控制方程

1.1 流场模拟控制方程

绝缘子周围的气流为湍流，为尽可能真实地模拟该流场，本文采用时间平均法，即把湍流分解为时间平均流动与瞬时脉动流动的叠加［12］。气流经过绝缘子时流线产生严重弯曲，在弯曲流线的情况下，湍流是各向异性的，因此本文选择RNG k-ε 模型，该模型考虑了平均流动中的旋转与旋流流动情况，可以更好地处理高应变率及流线弯曲程度较大的流动［13］。

不可压缩流体连续性方程为

式中:u 为速度矢量。

动量方程为

式中:μ 为空气动力粘度(温度20 ℃的值，18.08 ×10-6Pa·s);μT为空气湍流脉动附加动力粘度;ρ 为空气密度，1.205 kg/m3;k 为湍动能;I 为主应力张量。

RNG k-ε 模型的k 方程和ε 方程为

式中:k 为湍动能;ε 为湍流耗散率;粘度系数Cμ=0.09;模型常数σk=1.0、σε=1.3;湍流模型参数Cε1、Cε2为经验系数，一般取Cε1=1.45，Cε2=1.92;Pk为湍动能源项。

1.2 电场模拟控制方程

直流电场计算控制方程为

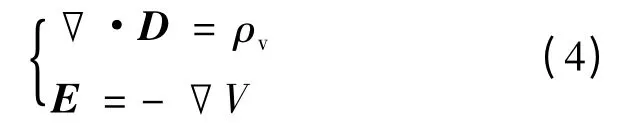
式中:D 为电位移强度，表达式为D = ε0ε1E;真空介电常数ε0=8.85 ×10-12F/m;ε1为各材料相对介电常数;ρv为体电荷密度;V 为电势。

1.3 颗粒运动控制方程

绝缘子周围的污秽颗粒在电场、空气流场和重力场的综合作用下运动。作用力主要有极化力、电场力、稳态曳力和重力，这些力决定了尘粒的运动特性。极化力非常小，对尘粒的运动不会产生影响，但可使尘粒在绝缘子表面粘附得更加牢固［10］。因此，假定颗粒运动过程中只受电场力、稳态曳力和重力的作用。

电场力为

式中:e 为原电荷量;z 为颗粒带原电荷的个数;E为电场强度。

重力为

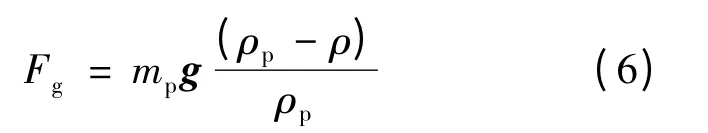
式中:mp为颗粒重量;ρp为颗粒密度;ρ 为空气密度;g 为重力加速度。

稳态流场的曳力为

式中:τp为粒子速度响应时间;u 为气体流速;v 为颗粒速度。

最终，颗粒运动特性方程为

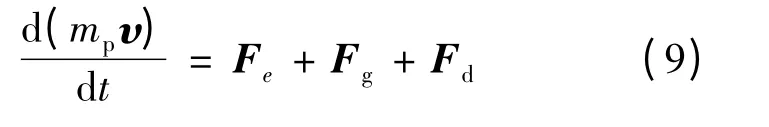
2 积污过程的模拟方法

2.1 模型建立及网格划分

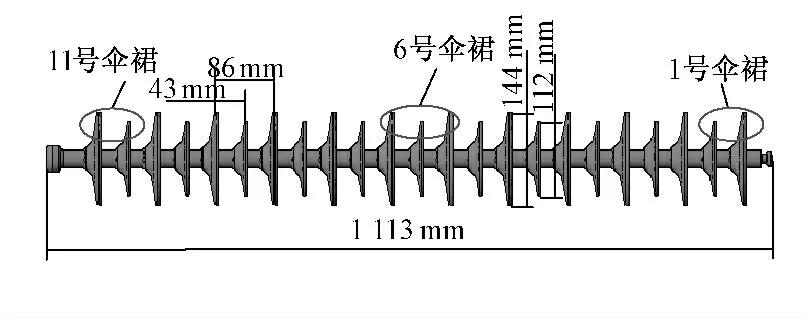
图1 FXBW-110/120-2 的结构简图Fig.1 Schematic diagram of FXBW-110/120-2

图2 计算区域网格示意图Fig.2 Schematic diagram of grid in computing area

以复合FXBW-110/120-2 绝缘子为研究对象，利用AutoCAD 软件进行建模，并对伞裙进行编号，其三维模型及其结构参数如图1所示。在COMSOL 中进行非结构化混合网格划分，距绝缘子越近网格越密，反之越疏，经网格无关性验证，最终确定总网格数约为77 万，计算区域网格示意图如图2所示(图中单位为m)。为更好地模拟电场分布，在六面体计算区域各表面设置100 mm 厚的无限元域，将无限元域作为电磁波在空间传播的吸收边界，以更好地接近实际情况。

2.2 边界条件的设定

对流场进行模拟时，将绝缘子周围空气视为不可压缩粘性定常流体，本研究侧重模拟自然环境微风条件下绝缘子的积污特性，模拟风速设为0.5 m/s、1 m/s、3 m/s、5 m/s、7 m/s，左侧为速度入口，右侧为压力出口。四个壁面为对称边界，采用壁面函数求解速度、压力分布。污秽颗粒设置为球形颗粒，考虑到微风条件下，空气环境中含量最大的悬浮物为小于15 μm 的颗粒物，为了使模拟接近自然环境，颗粒半径分别为5 μm、10 μm、20 μm，密度为2 200 kg/m3。对电场进行模拟时，颗粒随机带有0～600 个正/负基元电荷，总带电量为0。绝缘子1 号伞裙施加90 kV 直流电压为高压端，11 号伞裙接地为低压端。

3 模拟结果及分析

3.1 绝缘子外部流场分析

图3 为风速u =5 m/s 时，绝缘子表面的静压分布云图。绝缘子表面的静压反映了污秽颗粒与绝缘子表面相互作用的激烈程度，静压越大则相互碰撞越激烈。由图3 可以看出:绝缘子迎风面静压明显高于背风面静压，侧风面静压最小;迎风面的上伞面静压高于下伞面静压，背风面上下伞面静压差别不明显。静压对绝缘子积污的影响主要体现在大风速的情况，由于小风速下污秽颗粒与绝缘子表面的碰撞很弱，静压对其影响也较弱。

图3 u=5 m/s 的绝缘子局部表面静压分布云图Fig.3 The static pressure distribution of the insulator in the local surface when u=5 m/s

由流体力学知，当粘性流体绕流固体表面时，会在固体表面形成边界层，颗粒在该区域一旦被绝缘子表面捕获，很难逃逸。风速u =5 m/s 的气流速度场计算结果如图4所示(图中单位为m/s)。从图中可以看到，在绝缘子背风面形成局部低速回流区，颗粒在低速回区中容易由于惯性等作用而被分离出来，形成绝缘子表面积污。

3.2 绝缘子周围的电场与电位分布分析

图5 为90 kV 直流电压下绝缘子周围的场强分布图(图中单位为V/m)。由图5 可知:绝缘子高压端(1 号伞裙附近)场强最大;低压端(11 号伞裙附近)场强也有一定的集中，但比高压端低;绝缘子中段(6 号伞裙附近)场强较低且分布较均匀。

图6 为90 kV 直流电压下绝缘子周围的电位分布图。由图6 可知:绝缘子低压端电压最小值为15.8 kV;高压端电压最大值为51.7 kV;空间电压分布由两端向中间呈球面形扩散。

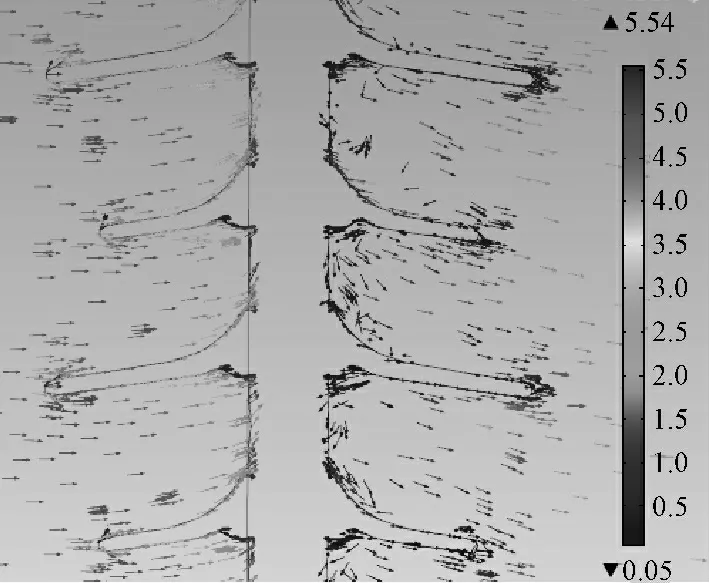
图4 u=5m/s 的局部速度矢量图Fig.4 The vector diagram in local surface when u=5m/s

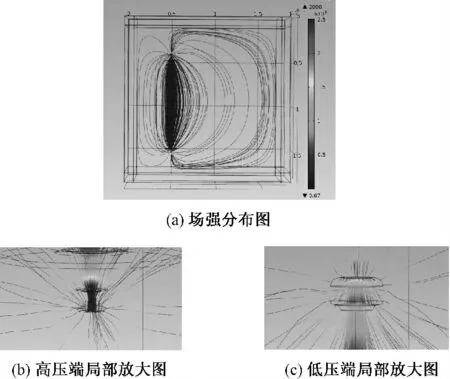
图5 90 kV 直流电压下绝缘子周围的场强分布图Fig.5 Field strength around the insulator under 90 kV DC

图6 90 kV 直流电压下绝缘子周围的电位分布云图Fig.6 The voltage distribution around the insulator under 90 kV DC

3.3 积污量分析

文献［14］在北京市西北部进行了自然积污试验，该地区风速一般不超过3 m/s，污秽颗粒主要为飘尘(粒径小于10 μm)。该试验中绝缘子从9月底投入运行，次年5 月份测得全表面的积污量为0.77 mg/cm2。为使模拟更加接近自然试验，模拟边界条件风速设为u =3 m/s 且粒径dp=10 μm，表1 为该边界条件下，施加90 kV 电压与无电压下绝缘子积污量的模拟结果对比(计算时长为7个月)，其中:积污量的定义为绝缘子单位表面积上的积污质量(单位为mg/cm2)。由表1 可知:该工况下，施加90 kV 电压时，全表面的积污量的模拟结果为0.85 mg/cm2。在边界条件接近的基础上，本模拟结果与文献［14］的试验结果在数量级上较为吻合;模拟结果略高于试验结果的主要原因是模拟中未考虑雨水冲刷的影响。

表1 风速为3 m/s 且粒径为10 μm 时施加90 kV 电压和无电压下绝缘子的积污量模拟结果对比Tab.1 Simulation results of contamination under 90 kV DC and without voltage when u=3 m/s and dp =10 μm

如表1所示，施加90 kV 电压时，从各伞裙积污量的分布看:绝缘子高压端(1 号伞裙附近)，由于其场强较大，电场力作用显著，其积污量相对于无电压的情况有较大增加;绝缘子低压端(11 号伞裙附近)，由于其场强也有一定的集中，但比高压端低，其积污量相对于无电压的情况有一定的增加，但增加量比高压端低;特别地，对于绝缘子中段(6 号伞群附近)其场强较低且分布较均匀，该部分绝缘子周围电场线近似与绝缘子轴线方向平行，电场力的作用最弱，其积污量虽然与无电压的情况比较增加不明显;但是，当颗粒运动到中段及相邻伞裙之间时，由于电场线的弯曲使电场力近似与绝缘子表面垂直，致使电场力在增加主流方向的的同时增加横向扰动，从而使颗粒垂直于主流方向的扰动增强，亦使中段及相邻伞裙面更容易形成积污。图7 为90 kV 直流电压作用下沿伞裙分布积污增量。由图7 可知:与不加电情况比较，施加90 kV 直流电压时，靠近高压端的2 号伞裙、绝缘子中段的5、6 号伞裙以及靠近低压端的11 号伞裙的积污量增量较大，呈“W”型分布。

图8 为积污量与风速和颗粒粒径的关系(计算时长为7 个月)，图9 为u =3 m/s 及u =1 m/s的积污量与粒径的关系。由图8 和图9 可知:绝缘子积污量随风速的增加而增加，风速较小时其增长速度较快，此时粒径对积污量的影响不大;在所研究的颗粒粒径范围内，绝缘子积污量随粒径的变化呈现先减小后增大的趋势，u =1 m/s 时5 μm 粒径的积污量最大，u =3 m/s 时20 μm 粒径的积污量最大。风速较小时，积污主要原因是颗粒的沉降，有利于小粒径颗粒的积污，此时5 μm粒径的积污量最大;随着风速的增大，小粒径颗粒对气流的跟随性增强，颗粒与绝缘子表面的碰撞对积污的影响逐渐增强，有利于大粒径的积污，故风速较大时，20 μm 粒径的积污量最大。由于未考虑沉积在绝缘子表面的污秽颗粒可能会被后续气流带走的现象，未出现积污量随风速的增大而减小的现象。

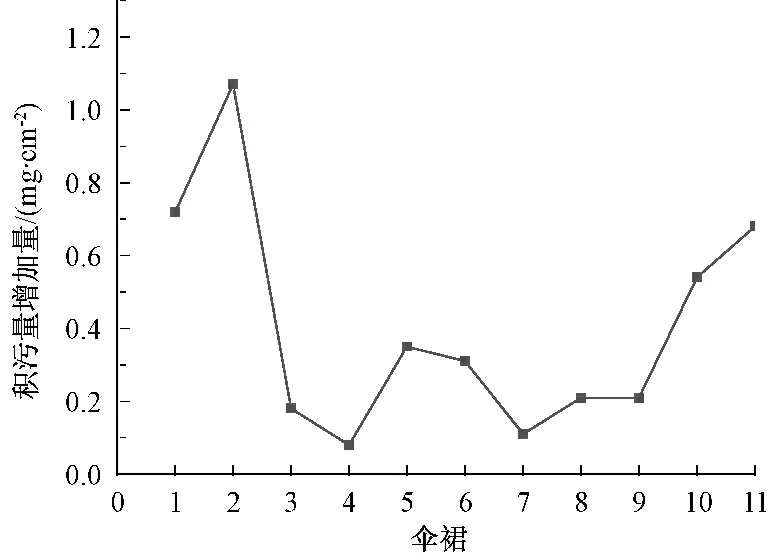
图7 90 kV 直流电压作用下沿伞裙分布积污增量Fig.7 Distribution along the umbrella skirt volume increment under the action of 90 kV DC

图10 为5 μm 粒径颗粒各伞裙积污量与风速关系。由图10 可知:各伞裙积污量均随风速的增大而增多;由于流场产生漩涡部位和电场强度的影响，靠近高压端的2 号伞裙和中间部分的6 号伞裙积污量最多，靠近低压端的10 号伞裙积污量最少;小风速下，颗粒的沉降作用抵消了一部分漩涡和电场强度的影响，不同伞裙积污量的波动较为平缓;大风速下，颗粒对气流的跟随性较强，沉降作用不明显，不同伞裙积污量的波动较为剧烈。

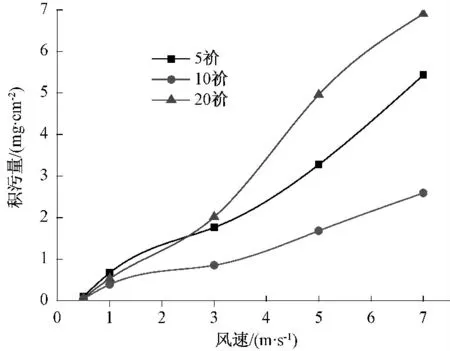
图8 积污量与风速和颗粒粒径的关系Fig.8 Relationship of the quantity of contamination with wind speed and particle size

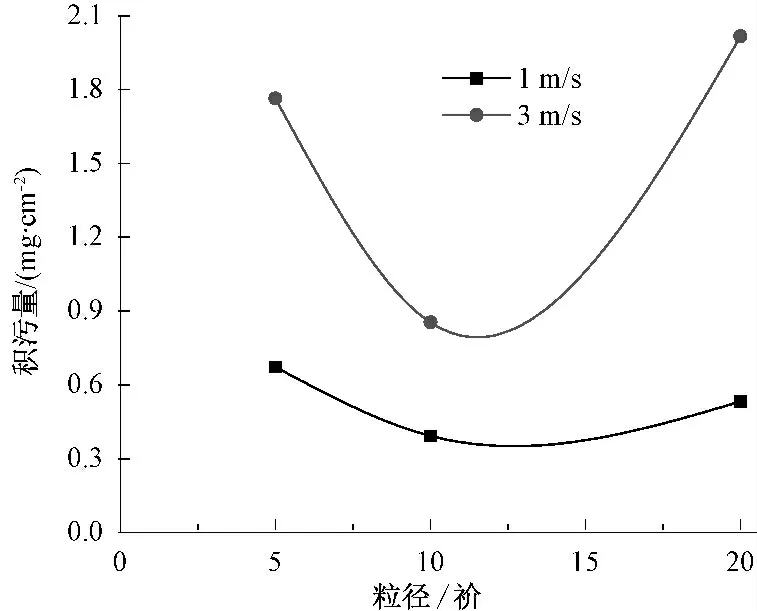
图9 u=3m/s 及u=1 m/s 的积污量与粒径的关系Fig.9 Relationship of the quantity of contamination and particle size when u=3m/s and u=1 m/s

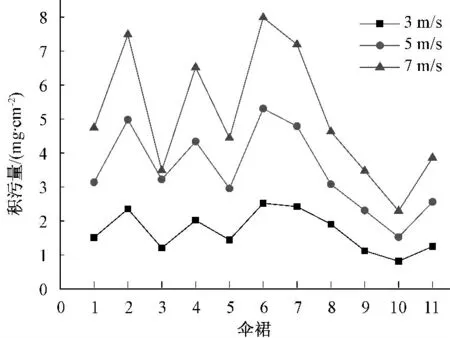
图10 5 μm 粒径颗粒各伞裙积污量与风速关系Fig.10 Relationship of the quantity of contamination of each umbrella group when particle size is 5 μm

4 结论

经验证，本模拟与文献［14］的试验结果较为吻合，通过对直流电压下风速、粒径对复合绝缘子积污特性影响的分析，可得出以下结论。

(1)复合绝缘子积污量随风速的增大而增多，随粒径的增大呈现先减小后增多的趋势。

(2)风速较小时，5 μm 粒径的积污量最多，风速较大时，20 μm 粒径的积污量最多。

(3)不同伞裙的积污量均随风速的增大而增大，小风速下不同伞裙积污量的波动较为平缓，大风速下，不同伞裙积污量的波动较为剧烈。

(4)与不加电情况比较，施加90 kV 直流电压时，靠近高压端的2 号伞裙、绝缘子中段的5、6 号伞裙以及靠近低压端的11 号伞裙的积污量增量较大，呈“W”型分布。

［1］李海波.基于流体力学原理的悬垂绝缘子串积污特性研究［D］.重庆:重庆大学，2010.

［2］蒋兴良，易辉.输电线路覆冰及防护［M］.北京:中国电力出版社，2001.

［3］宿志一，刘燕生.我国北方内陆地区线路与变电站用绝缘子的直、交流自然积污实验结果的比较［J］.电网技术，2004，28 (10):13-17.

［4］夏谷林，卢喜龙，赖光霖.运行中500kV 输电线路绝缘子串自然积污及污闪特性研究［J］.电网技术，2013，41 (4):24-30.

［5］李武峰，范建斌，李鹏.直流绝缘子串污秽闪络特性研究［J］.电网技术，2006，30 (15):21-24.

［6］Ravelomanantsoa N，Farzaneh M，Chisholm W.Insulator pollution processes under winter conditions［C］.proceedings of the electrical insulation and dielectric phenomena，2005 CEIDP′05 annual report conference on，F，2005:321-324.

［7］Ravelomanantsoa N，Farzaneh M，Chisholm W.A simula-tion method for winter pollution contamination of HV insulators［C］.proceedings of the Electrical Insulation Confer-ence (EIC)，2011，F，2011.

［8］谢从珍，张尧，郝艳捧.±800 kV 特高压直流悬式复合绝缘子伞形的风洞模拟［J］.高电压技术，2010，(1):216-217.

［9］Farzaneh M，Baker T，Bernstorf A，et al.Insulator icing test methods and proce-dures:a position paper prepared by the IEEE task force on insulator icing test methods［J］.Power Delivery，IEEE Transactions on，2003，18 (4):1503-1505.

［10］王晶，陈林华，刘宇.电场对复合绝缘子积污特性影响的探究［J］.高电压技术，2011，37 (3):585-591.

［11］王刚，安琳.COMSOL Multiphysics 工程实践与理论仿真:多物理场数值分析技术［M］.北京:电子工业出版社，2012.

［12］王福军.计算流体动力学分析-CFD 软件原理与应用［M］.北京:清华大学出版社，2004.

［13］蒋兴良，李海波.计算流体动力学在绝缘子积污特性分析中的应用［J］.高电压技术，2013，36 (2):329-334.

［14］李震宇，梁曦东.直流电压下复合绝缘子的自然积污试验［J］.电网技术，2007，31 (14):10-14.