多无人机协同搜索区域分割与覆盖
2015-12-19于驷男周锐夏洁车军
于驷男,周锐*,夏洁,车军
(1.北京航空航天大学 飞行器控制一体化技术重点实验室,北京100191;2.中航工业 西安飞行自动控制研究所,西安710065)
多机协同搜索是无人机协同的重要任务之一,覆盖搜索要求无人机在一定的约束条件下能够将待搜索区域无遗漏地遍历搜索.
目前,国内外对于单无人机覆盖搜索有较多研究,常见的搜索策略有随机搜索、平行搜索、网格搜索等[1],文献[2-3]都对单机覆盖的搜索策略和方向进行了阐述,文献[4]应用A*算法对无人机的搜索侦查路径进行了规划.但是单机受传感器探测范围、飞行时间、燃油量等限制,在许多情况下难以实现有效搜索,而多无人机协同搜索就可以满足更多的搜索任务需求.多机协同搜索的本质也是一种路径规划问题,其重点在数学建模、环境表示和规划算法[5].针对这3点展开的研究是非常丰富的.文献[6]使用高斯混合模型解决无人机启发式覆盖搜索问题;文献[7]仿照生物信息素设计了基于数字信息素的搜索方法;文献[8]提出了道路网络中多机搜索策略及实时路径规划方案;文献[9]应用分层模糊推理评估无人机性能、分配任务;文献[10]提出了对运动目标适用的编队覆盖搜索方法.这些方法都较为复杂,并会产生较多的重复搜索.多机搜索与单机搜索的一个差异在于多机之间需要进行通信,文献[11]探讨了信息融合与通信延时对多机协同搜索的影响,这也是近几年研究的热点.
将多无人机搜索区域进行分割后,每个子区域内只有一架无人机,问题就简化为子区域内的单机覆盖搜索.在无人机搜索领域,如文献[12-13]中所述应用Voronoi图对搜索区域进行分割的方法非常普遍,但这种分割非常复杂,并且带有不确定性,对无人机的自主性要求也较高.
本文详细分析了无人机覆盖搜索路径,借鉴并完善文献[14]的思路对凸多边形搜索区域进行分割,根据无人机的特点评估分割结果,并仿真验证了方法的实用性.
1 搜索策略的确定
无人机搜索传感器探测区域如图1所示.不考虑无人机姿态角变化,传感器高度h处的探测范围是一半径为R=h·tanθ的圆[4].

图1 传感器探测范围示意图[4]Fig.1 Detection range of sensor[4]
覆盖搜索最常用的策略之一是平行搜索,因无人机的搜索轨迹呈平行线而得名[15].与机器人覆盖搜索不同,无人机存在最小转弯半径约束,需要在待搜索区域外部进行转弯飞行.这一段飞行相对搜索区域是没用的,如能减少搜索转弯次数,就可减少飞行路程、搜索时间和油耗.如图2所示,若按左图搜索,总路程为27.708 0单位长度,而按右图搜索,总路程只有21.2832单位长度.所以对某覆盖搜索区域,要确定一个搜索方向,使得沿此方向搜索的转弯次数尽量少.
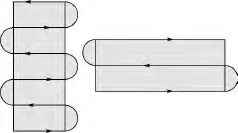
图2 搜索方向对总路程的影响Fig.2 Effect of search direction on search distance
由于无人机的探测范围半径R在飞行高度和探测器角度恒定时为定值,若搜索区域的宽度是L,转弯次数的计算方法是
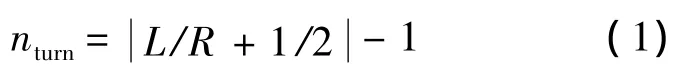
由此可见,计算出搜索区域的最小宽度Lmin,即可保证搜索过程中拥有最少转弯次数.
这里引用文献[16]对最小宽度Lmin的定义:在平面上做两条相距足够远的平行线,当平行线逐渐向其中心靠拢与凸多边形相交时即刻停止,两平行线之间的距离就定义为凸多边形的宽度.所有跨度中的最小值称为凸多边形的最小宽度.
如图3所示,Lmin即为多边形ABCDE的最小宽度,其对应顶点为A,对应边为CD.
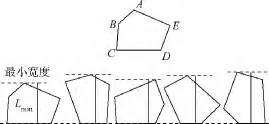
图3 多边形的最小宽度Fig.3 The minimal width of polygon
2 平行搜索路径分析
2.1 搜索起始点的选取
为了简化问题,可先将搜索区域旋转至一个便于分析搜索路径的方向.设多边形顶点序列为V,可取最小宽度对应的边ViVi+1为x轴,该边一端点Vi或Vi+1为原点.原点并不一定是搜索起始点.如图4所示,细实线表示搜索边界,粗实线表示平行航路以及在搜索区域外部的延长线,虚线表示无人机的传感器探测边界以及在搜索区域外部的延长线.若选择搜索区域顶点,即起始点1作为搜索起始点,则会出现遗漏区域,若选择图起始点2作为搜索起始点就可以避免遗漏.
所以搜索起始点的选取方法为:在第1条探测边界与搜索边界交点和搜索边界顶点中,选择横坐标较小的点.
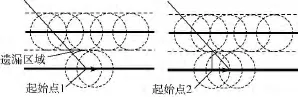
图4 起始点的选取Fig.4 Selection of the beginning point
2.2 转弯关键点的确定
先假设最小转弯半径r与探测范围半径R相等.如图5所示,搜索边界左侧为搜索区域内部.称开始调头的点A为“调头点”,调头结束的点B为“结束点”.
观察图6所示的情况,当搜索边界斜率较大时,若所有的调头点和结束点都处在边界上,就可能出现遗漏的情况.为了防止遗漏区域的产生,调头点与结束点不能简单地在搜索边界上选取.
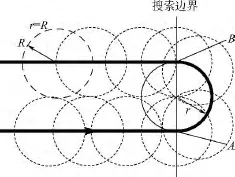
图5 调头点与结束点Fig.5 Turn start point and turn end point

图6 遗漏区域的产生Fig.6 Omission area
首先定义相对方向相同和相对方向相反:无人机在掉头点的行进方向(沿x轴正向取“+”,负向取“-”)与其所处搜索边界的斜率符号相同,则称相对方向相同,否则称相对方向相反.
如图7所示,根据搜索方向的不同分为4种情况(Ⅰ~Ⅳ)进行讨论.情况Ⅱ和Ⅲ中相对方向相同,调头点在搜索边界上,结束点的横坐标应等于后一条探测边界(虚线)与搜索边界交点的横坐标(竖直实线所示).情况Ⅰ和Ⅳ中相对方向相反,结束点在搜索边界上,调头点的横坐标应等于前一条探测边界与搜索边界交点的横坐标.
所以转弯关键点的确定方法为:当飞行方向为x轴正(负)方向时,搜索边界与当前直线航路的交点、与当前探测上边界的交点、与当前下边界的交点,这3个点的横坐标最大(小)值应该被选取为调头点或结束点的横坐标.需要注意的是,沿x轴正向(负向)飞行的结束点的横坐标最大(最小)不能大于(小于)航路与搜索边界交点的横坐标,同理沿x轴正向(负向)飞行的调头点的横坐标最小(最大)不能小于(大于)航路与搜索边界交点的横坐标,否则就取该交点的横坐标.
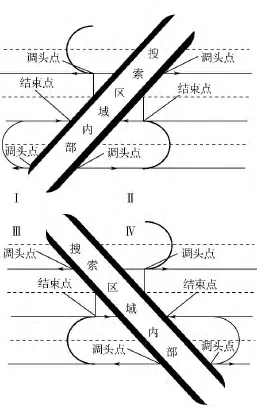
图7 调头点与结束点的选取Fig.7 Selection of turn start point and turn end point
2.3 最小转弯半径对路径的影响
无人机在搜索区域外的航路可认为是在最小转弯半径约束下,从调头点至结束点的最短路径问题.由最小转弯半径r和无人机探测区域半径R的关系,分为两种情况.
1)r<R时的情况.
给定调头点A和结束点B,实际转弯路径为图8中粗实线所示.无人机航迹是两段圆心角分别为π/2+α和β的圆弧和一条直线段组成的.图8所示为飞行方向为x轴正向的两种情况,区别在于航迹经过两段圆弧的顺序.飞行方向为负时有类似的结果.

图8 r<R时的转弯航路Fig.8 Turning route when r< R
2)r≥R时的情况.
当r≥R时,无人机航迹是由两段圆心角分别为3π/2-β和α的圆弧组成的.图9中粗实线所示为飞行方向为x轴正向的两种临界情况,即A与B的横坐标恰好满足:
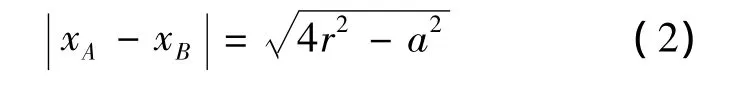
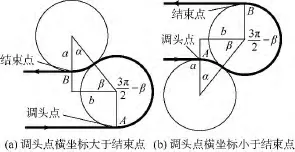
图9 r≥R时临界情况的转弯航路Fig.9 Critical situation of turning route when r≥R
在式(2)不成立时,需补充一段直线航路.图9(a)情况对应图10(a),若结束点横坐标小于临界结束点B横坐标(B1),则先按临界情况(虚线)转弯,到达B点后,再直线行进一段长度为ΔS1的线段;若结束点横坐标大于临界结束点B横坐标(B2),则先行进一段长度为ΔS2的线段到达A2点,然后再进行转弯.图 9(b)的情况对应图10(b),有着类似的结果.结束点与临界结束点之间的距离ΔS由式(3)计算.

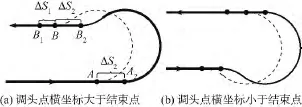
图10 r≥R时非临界情况的转弯航路Fiig.10 Non-critical situation of turning route when r≥R
2.4 搜索终点的确定
搜索终点本质是调头点,只是不再进行转弯.所以可得出与2.2节类似的结论,当飞行方向为x轴正(负)向时,搜索边界与当前直线航路的交点、与当前探测上边界的交点、与当前下边界的交点,这3个点的横坐标最大(小)值应该被选取为搜索终点的横坐标.
图11所示是飞行方向沿x轴正向时的搜索终点情况.当飞行方向沿x轴负方向时,得到的结论是一致的.
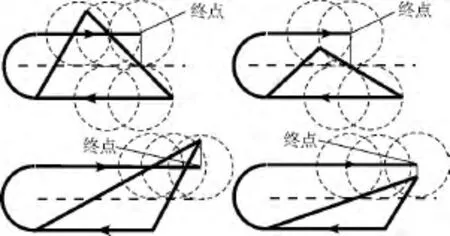
图11 搜索终点的选取Fig.11 Selection of the ending point
3 搜索区域分割
3.1 凸多边形分割算法
设凸多边形搜索区域P顶点序列V(P)按逆时针排列.区域内有N架无人机执行搜索任务,每架无人机负责搜索的面积各不相同.多边形P中无人机的数量用s(P)表示,无人机位置、搜索面积等用S(P)表示.区域分割的目的是用N-1条线段,将P分割成N个子多边形,每个子多边形中包含一架无人机,且该子多边形的面积等于其包含无人机需要搜索的面积[14].
若在第1步分割后,分开的两部分各包含n1和n2架无人机,且n1≠1或n2≠1,下面分割哪个多边形,在文献[14]中并未提及.解决这个问题可以借鉴广度搜索的思想,使用一个初值为V(P)的队列,标志位为1.然后将每一次分割过后s(P)≠1的多边形顶点序列放入队列尾部,标志位向后移动一位,最终可实现将 P分割成 N部分.
3.2 选择分割方案
对凸多边形区域应用上述算法分割,当顶点次序不同时(即改变初始顶点V1,其他顶点逆时针顺次排序),分割结果也不同.即对凸M多边形,用一条线段将其分割成两部分会有M种结果.如图12所示,要把S1(30%)和S2(70%)分割开,分别以4个顶点作为 V1,有4种分割结果.
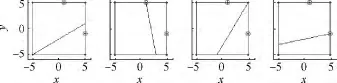
图12 顶点序列顺序不同时的分割结果Fig.12 Decomposition results under different orders of vertices
对有k架无人机的搜索区域,每架无人机在各自搜索子区域内的转弯次数为ni,则总转弯次数为

结合第1节的论证,将全部无人机的总转弯次数作为分割结果的评判标准.在若干种分割结果中,选取N值最小的作为最终的分割结果.
3.3 从初始位置到搜索起始点的路径
将搜索区域分割后,无人机所在的初始位置很可能不在2.1节所讨论的搜索起始点上,所以在搜索开始前,要先将无人机从初始位置移动到搜索起始点.设无人机初始位置与搜索起始点的间距为D,这个过程受最小转弯半径r的限制,路径可能出现D>r或D≤r两种情况.
1)D>r情况.
如图13所示,从初始位置S沿直线移动到切点B,然后按最小转弯半径飞至A点,即可开始平行搜索.切点B可由以下方程组求解:

然后通过B点坐标可求得圆心角θ,进而航路得以解算.
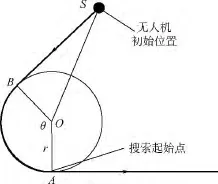
图13 D>r时的起始路径Fig.13 Initial route when D > r
2)D≤r情况
如图14所示.无人机先按最小转弯半径沿圆周运动,再经一段直线到达搜索起始点.当yS>yO时,如S1位置所示,B1坐标与θ值可用下式计算:
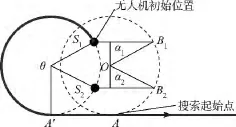
图14 D≤r时的起始路径Fig.14 Initial route when D≤r


当yS<yO时,如S2位置所示,B2坐标也由式(6)计算,θ的计算公式为

4 仿真结果
仿真算例1:设3架无人机覆盖搜索某随机生成的五边形区域.搜索区域顶点坐标序列为
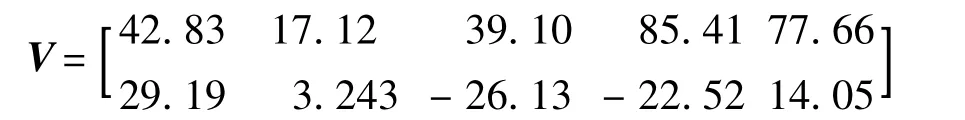
无人机坐标序列为
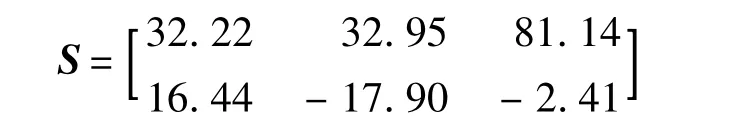
设搜索面积百分比分别为20%,30%,50%,最小转弯半径r分别为1,2,3,探测范围半径R均为2.顺次变换顶点V1的位置,有5种分割方式,选取总转弯次数最少的一种,总转弯次数为16次,如图15所示.覆盖搜索结果如图16所示.仿真算例2:设4架无人机覆盖搜索某正六边形区域.搜索区域顶点坐标序列为
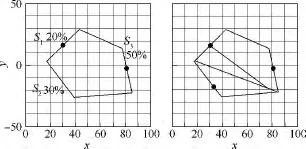
图15 包含3架无人机的随机五边形搜索区域及分割结果Fig.15 A random pentagon search area including 3 UAVs and decomposition result
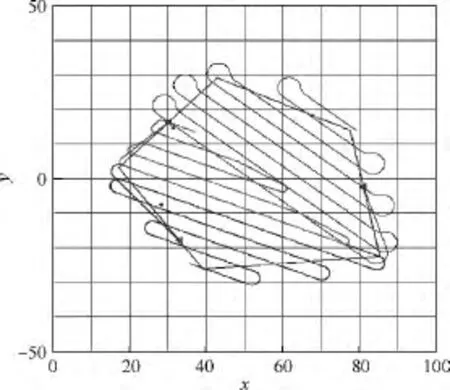
图16 3架无人机对随机五边形搜索区域的覆盖结果Fig.16 Coverage result of 3 UAVs in a random pentagon search area

无人机坐标序列为

设搜索面积百分比分别为10%,20%,30%,40%,最小转弯半径 r分别为 1,2,2,4,探测范围半径R均为2.顺次变换顶点V1的位置,有6种分割方式,选取总转弯次数最少的一种,总转弯次数为24次,如图17所示.无人机覆盖搜索结果如图18所示.
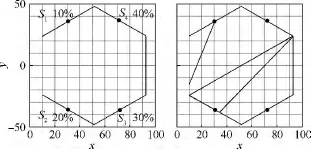
图17 包含4架无人机的正六边形搜索区域及其分割结果Fig.17 A regular hexagon search area including 4 UAVs and the decomposition result
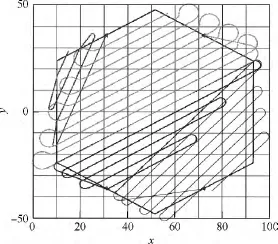
图18 4架无人机对正六边形搜索区域的覆盖结果Fig.18 Coverage result of 4 UAVs in a regular hexagon search area
5 结论
1)本文对多无人机在凸多边形搜索区域内的覆盖协同搜索问题进行了研究.通过一种凸多边形分割算法,将待搜索区域分割成为若干子区域,把多无人机协同搜索问题转化为子区域内的单机覆盖搜索问题.这种分割方法基于无人机的初始位置和负责搜索的面积大小,可以有针对性地对不同无人机制定搜索方案.这种分割方法可以给出多种分割结果,以全部无人机的总转弯次数最少作为评估准则,转弯次数最少即为飞行路程最短,从而得到最优的分割结果.
2)本文使用Z字形平行搜索策略,可以实现搜索区域的无遗漏覆盖.为了确保这一点,对搜索路径中各关键点进行了分析,详细讨论了搜索起始点、转弯关键点、搜索终点的选取.并且针对飞行器最小转弯半径对飞行的影响,具体讨论、计算了各种参数条件下的路径.并将多机协同的强耦合任务转为弱耦合任务,在无遗漏覆盖的基础上降低重复搜索,提高了搜索效率.通过仿真结果验证了方法的有效性.
3)在今后的研究中还可以进一步验证螺旋状平行搜索、间隔平行搜索等策略对飞行路程的影响.另外如果地形起伏较大,还需要考虑地面高度对搜索的影响.
References)
[1] George J,Sujit P B,Sousa J B.Search strategies for multiple UAV search and destroy missions[J].Journal of Intelligent &Robotic Systems,2011,61(1-4):355-367.
[2] Huang W H.Optimal line-sweep-based decompositions for coverage algorithms[C]//Proceedings of the IEEE International Conference on Robotics and Automation.Seoul:IEEE,2001,1:27-32.
[3] Araujo J F,Sujit P B,Sousa J B.Multiple UAV area decomposition and coverage[C]//Computational Intelligence for Security and Defense Applications(CISDA).Singapore:IEEE,2013:30-37.
[4] 李子文,夏洁.无人侦察机路径规划方法研究[J].系统仿真学报,2008,20(z1):490-494.Li Z W,Xia J.Reconnaissance path planning for UAV[J].Journal of System Simulation,2008,20(z1):490-494(in Chinese).
[5] 袁利平,夏洁,陈宗基.多无人机协同路径规划研究综述[J].飞行力学,2009,27(5):1-5.Yuan L P,Xia J,Chen Z J.Survey on multiple UAV cooperatice path planning research[J].Flight Dynamics,2009,27(5):1-5(in Chinese).
[6] Lin L,Goodrich M A.Hierarchical heuristic search using a Gaussian mixture model for UAV coverage planning[J].IEEE Transactions on Cybernetics,2014,44(12):2532-2544.
[7] 沈东,魏瑞轩,茹常剑.基于数字信息素的无人机集群搜索控制方法[J].系统工程与电子技术,2013,35(3):591-596.Shen D,Wei R X,Ru C J.Digital-pheromone-based control method for UAV swarm search[J].Systems Engineering and E-lectronics,2013,35(3):591-596(in Chinese).
[8] Dille M,Singh S.Efficient aerial coverage search in road networks[C]//AIAA Guidance,Navigation,and Control(GNC)Conference.Reston,VA:AIAA,2013:1-20.
[9] 彭辉,沈林成,霍霄华.多UAV协同区域覆盖搜索研究[J].系统仿真学报,2007,19(11):2472-2476.Peng H,Shen L C,Huo X H.Research on multiple UAV cooperative area coverage searching[J].Journal of System Simulation,2007,19(11):2472-2476(in Chinese).
[10] 轩永波,黄长强,吴文超,等.运动目标的多无人机编队覆盖搜索决策[J].系统工程与电子技术,2013,35(3):539-544.Xuan Y B,Huang C Q,Wu W C,et al.Coverage search strategies for moving targets using multiple unmanned aerial vehicle teams[J].Systems Engineering and Electronics,2013,35(3):539-544(in Chinese).
[11] Mirzaei M,Gordon B W,Rabbath C A,et al.Cooperative multi-UAV search problem with communication delay[C]//AIAA Guidance,Navigation,and Control Conference.Toronto,Ontario Canada:AIAA,2010,8420:1-11.
[12] Pehlivanoglu Y V.A new vibrational genetic algorithm enhanced with a Voronoi diagram for path planning of autonomous UAV[J].Aerospace Science and Technology,2012,16(1):47-55.
[13] Guruprasad K R,Ghose D.Automated multi-agent search using centroidal voronoi configuration[J].IEEE Transactions on Automation Science and Engineering,2011,8(2):420-423.
[14] Hert S,Lumelsky V.Polygon area decomposition for multiplerobot workspace division[J].International Journal of Computational Geometry & Applications,1998,8(4):437-466.
[15] Bolonkin A,Cloutier J R.Search and attack strategies[C]//2005 AIAA Guidance,Navigation,and Control Conference and Exhibit.Rhode Island:AIAA,2005:1-12.
[16] 陈海,王新民,焦裕松,等.一种凸多边形区域的无人机覆盖航迹规划算法[J].航空学报,2010,31(9):1802-1807.Chen H,Wang X M,Jiao Y S,et al.An algorithm of coverage flight path planning for UAVs in convex polygon areas[J].Chinese Journal of Aeronautics,2010,31(9):1802-1807(in Chinese).
