基于舵机指令前馈的电液负载模拟器同步控制
2015-12-19韩松杉焦宗夏尚耀星汪成文
韩松杉,焦宗夏*,尚耀星,汪成文
(1.北京航空航天大学 自动化科学与电气工程学院,北京100191;2.北京航空航天大学 飞行器控制一体化技术重点实验室,北京100191)
负载模拟器是飞行器伺服机构半实物仿真的主要设备,用于模拟舵机在飞行过程中所承受的气动载荷,其性能直接影响飞控系统伺服机构评价的置信度[1].负载模拟器的成功应用不但可以缩短飞行器的研制周期、降低研制成本,而且可以提高飞行器研制的成功率.根据实现形式,负载模拟器可分为机械式[2]、电液式[3]、电动式[4]和气动式[5]4种.其中电液负载模拟器具有功率密度大、响应速度快、电磁兼容性好等优点而得到广泛的研究和关注.因此,研究高精度的电液负载模拟器具有重要的现实和战略意义
由于电液负载模拟器的施力对象为位置伺服系统,故其是典型的带有强运动耦合的电液力伺服系统.有研究者将此运动扰动引起的力矩干扰称之为多余力(矩)[6],针对如何抑制多余力的问题国内外相关学者开展了广泛的研究,其方法大体分为3类:第1类是结构补偿方法.其从加载系统的硬件(机械)结构入手,通过增加辅助环节来消除多余力或力矩.例如:安装连通孔、缓冲弹簧校正、蓄压器校正、双伺服阀流量补偿控制、双马达位置同步补偿等方法[7-8].总体来说此方法的结构比较复杂,成本也比较高.第2类是基于同步补偿的控制算法.该类方法是从控制策略入手,采用补偿网络在加载系统中产生附加速度同步控制作用,达到克服多余力或力矩的目的.文献[6]提出了“结构不变性理论”,利用舵机系统的速度反馈信息进行前馈补偿,其研究揭示了舵机速度是影响多余力的主要原因,为以后关于多余力研究奠定了基础[9-10].焦宗夏等人提出了速度同步控制算法,通过采用舵机的阀信号来实现速度同步,在工程中得到了大量应用[1,3,11].基于系统模型的速度前馈补偿消除多余力的研究也被广泛讨论.姚建勇等人提出了一种最优模型补偿控制策略,并针对系统模型的不确定性设计了一种自适应鲁棒力矩控制策略,取得了良好效果[12-13].第3类方法是将运动耦合看作一种外干扰,通过提高力伺服系统的鲁棒性消除位置系统的影响,如定量反馈控制[14]、H∞控制[15]、μ 理论[16]等.此外,摩擦对力矩跟踪性能也有较大影响[17],针对静态加载工况下的力矩跟踪,文献[18]设计了一种基于LuGre摩擦模型的双状态估计鲁棒控制策略,提升了系统跟踪精度.
目前在工程实践中,基于舵机速度的结构不变性方法[6,10]及基于舵机电流的速度同步算法[1,11]由于其结构简单、计算量小、可实现性好等优点在电液负载模拟器消除多余力中得到广泛采用.本文在两者基础上,提出了基于舵机速度指令前馈的同步补偿策略.该策略尤其适用于部分一体化舵机无法提供速度反馈信号、舵机控制阀电流以及舵机电流噪声过大而导致结构不变性方法和速度同步算法无法有效应用的实际测试工况.该策略充分利用舵机可提供的速度指令前馈信号与负载模拟器自身力矩传感器信号来实现精确的速度同步补偿,有效避免结构不变性方法对高品质舵机速度或加速度信号的要求,相对于传统的速度同步算法不需要舵机提供伺服阀控制信号,并能实现在大负载跟踪下更好的多余力消除,进而提高系统的消扰能力及动态加载精度.
1 负载模拟器系统模型
电液负载模拟器的典型结构如图1所示.示意图的右边为电液负载模拟器,由加载液压马达、加载伺服阀、力矩传感器、惯量负载等组成.电液负载模拟器的功能就是在位置伺服系统运动的过程中实现准确的力加载,故负载模拟器亦称为加载系统;示意图的左边为位置伺服系统(舵机系统),由舵机伺服阀、角度传感器等组成.加载系统与舵机相互耦合,对舵机而言,加载力矩对于其位移输出具有很强的干扰,从而影响其位移输出精度;而对于加载系统来说,舵机的运动作为强干扰,同样严重地影响加载系统的控制精度.
1.1 加载系统建模
加载伺服阀流量方程[19]:
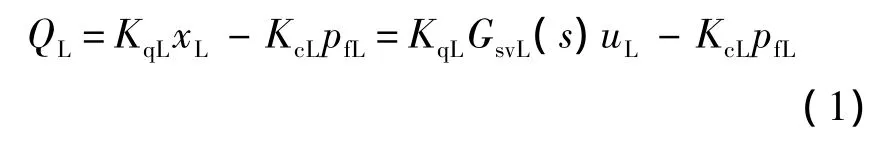
式中,QL为加载系统伺服阀流量;xL为加载系统伺服阀阀芯;pfL为加载系统负载压力;KqL为加载系统伺服阀的流量增益;uL为加载系统伺服阀的控制电压;KcL为加载系统伺服阀流量压力系数;GsvL(s)为加载系统伺服阀阀芯位移驱动动态函数;s为Laplace算子.
加载液压马达流量连续方程:
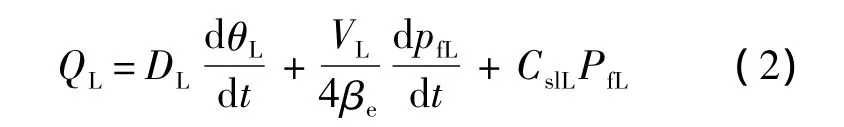
式中,DL为加载液压马达弧度排量;θL为加载液压马达转子角位移;VL为加载液压马达控制容积;CslL为加载液压马达泄漏系数;βe为液压油弹性模量.
加载液压马达转子力矩平衡方程:

式中,JL为加载液压马达转动惯量;BL为加载液压马达黏性阻尼系数;Gs为力矩传感器与传动轴的综合刚度;θa为力矩传感器与被加载对象连接端角位移.

图1 电液负载模拟器及舵机系统结构示意图Fig.1 Structure diagram of load simulator and actuator system
输出力矩为

式中T为加载系统输出力矩.
结合式(1)~式(4)给定的加载系统数学模型,可得加载系统的输出力矩传递函数为
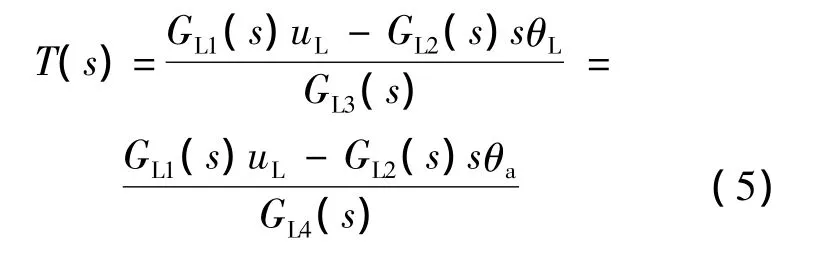
式中 GL1(s)=DLKqLGsvL(s)其中KtmL为加载系统的总流量压力系数.
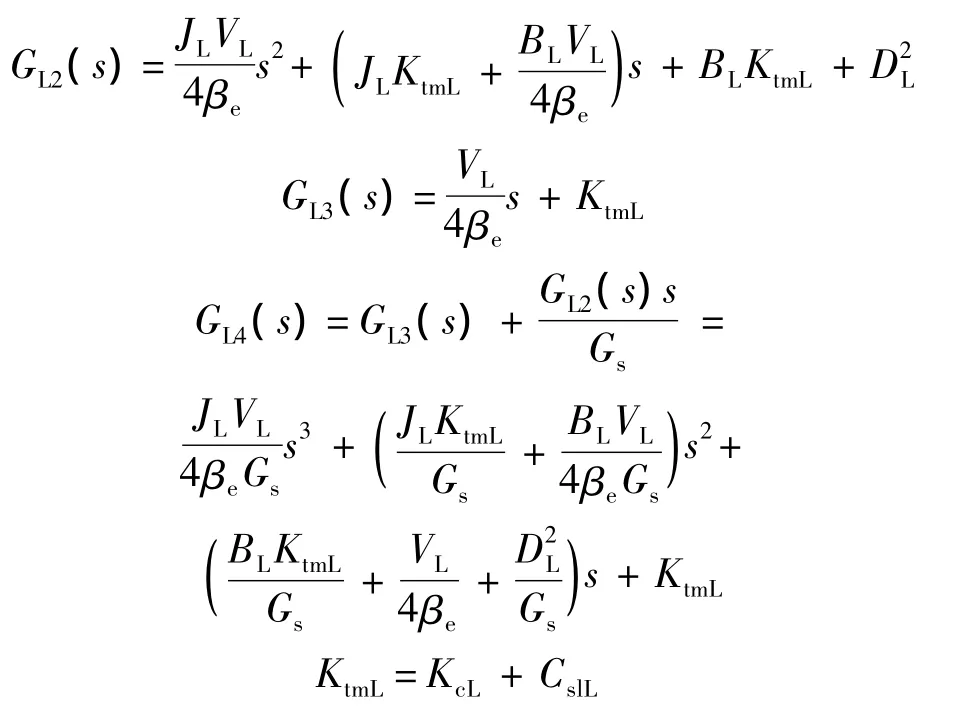
1.2 舵机系统建模
舵机伺服阀流量方程[19]:
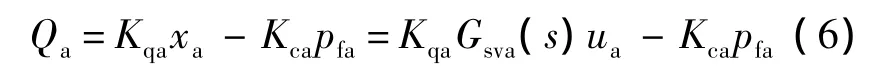
式中,Kqa为舵机伺服阀的流量增益;xa为舵机伺服阀阀芯位移;Kca为舵机伺服阀流量压力系数;pfa为舵机压差信号;Gsva(s)为舵机伺服阀阀芯位移驱动函数;ua为舵机伺服阀控制电压.
舵机液压马达流量连续方程:
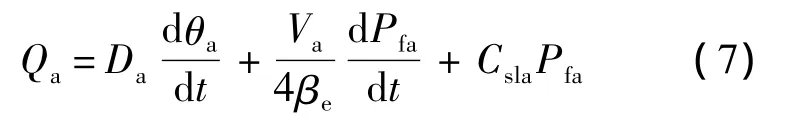
式中,Da为舵机液压马达弧度排量;Va为舵机液压马达控制容积;Csla为舵机液压马达泄漏系数.舵机液压马达转子力矩平衡方程:

式中,Ja为舵机液压马达转动惯量;Ba为舵机液压马达黏性阻尼系数.
舵机伺服阀电流的计算过程:

式中,Gc(s)为舵机控制器;θd为舵机角度指令.
2 传统同步控制方法分析
从加载力矩的输出方程(5)可知,舵机系统的运动对加载系统的干扰是速度的函数.正是舵机速度扰动的存在,往往导致加载系统的传统PID控制效果不好.故结构不变性原理是利用承载对象的速度进行前馈控制来达到消除多余力(矩)的目的[6,9-10].其原理示意图如图2所示.
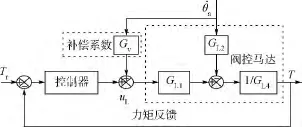
图2 结构不变性示意图Fig.2 Principle diagram of structure invariance method
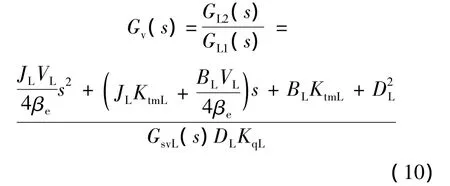
但实际应用中由于Gv(s)含有速度的高阶微分、模型误差、伺服阀的动态特性、非线性和参数时变等因素,使得Gv(s)的设计和实现比较困难,故结构不变性方法通常将补偿环节简化为常数.另一方面由于速度传感器的精度和安装等问题,高质量的速度信号难以得到,从而限制了多余力矩的消除效果.既然角度采集电路微分后的速度信号(含噪声和相位滞后)和角速度传感器的信号满足不了要求,于是文献[1]提出了速度同步算法,采用舵机伺服阀信号去近似舵机速度,该信号噪声小、滞后很少并相对舵机速度而言具有超前补偿效果,在工程实际中已证明其能有效消除多余力,因此目前该方法在实践中得到广泛的应用,其补偿原理如图3所示.
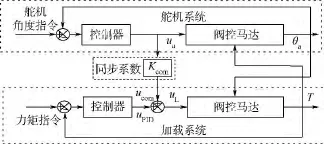
图3 传统速度同步方法示意图Fig.3 Principle diagram of traditional velocity synchronizing method
但是在实际使用的工况中,部分一体化舵机无法提供舵机电流或舵机电流噪声过大,此时传统的速度同步方法无法使用.故本文提出基于舵机速度指令前馈的速度同步方法,只需要舵机速度指令信号,不需要舵机电流信号,亦不需要舵机的角度、速度及加速度等传感器信号,更容易在工程上应用.
3 改进型速度同步补偿算法
由舵机伺服阀流量方程(6)及马达流量连续性方程(7)可得舵机速度的表达式:
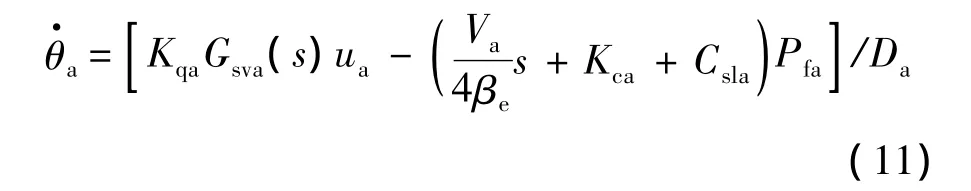
由式(8)~式(9)、式(11),可得
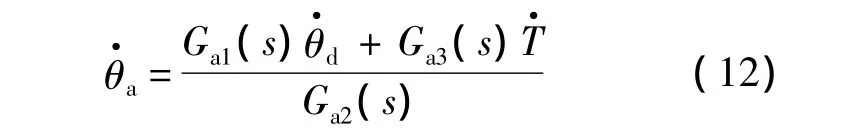
式中
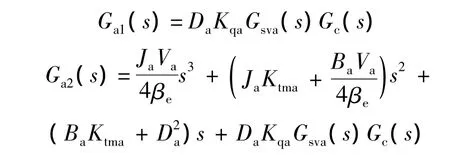
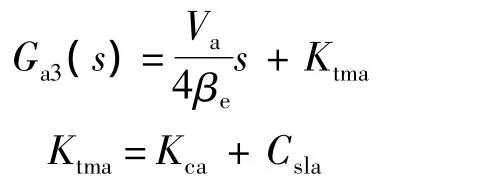
Ktma为舵机系统的总流量压力系数.
从式(5)和式(12),可得
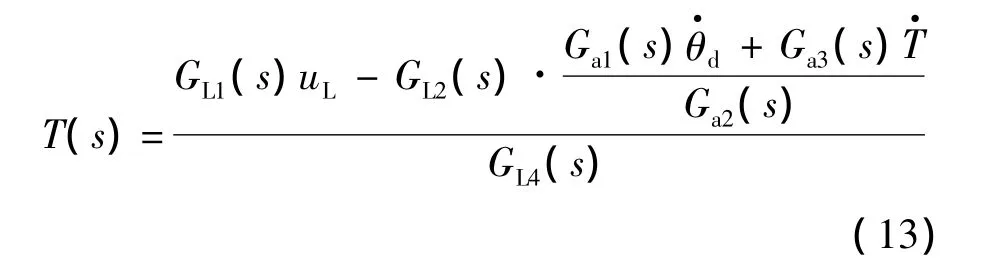
故消除舵机速度对加载系统的影响,就转化为消除式(13)中的舵机速度指令和力矩采样微分对加载系统力矩输出的影响.加载系统的同步补偿环节应为

式中


故控制器可设计为
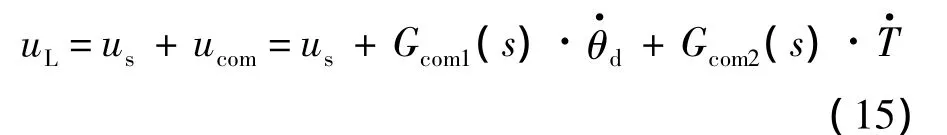
式中us为基于力矩误差的闭环鲁棒项.
该改进型速度同步算法的补偿框图如图4所示.
式(15)代入式(13),可得
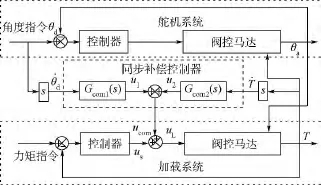
图4 改进型速度同步补偿算法原理图Fig.4 Principle diagram of the improved synchronizing compensation algorithm
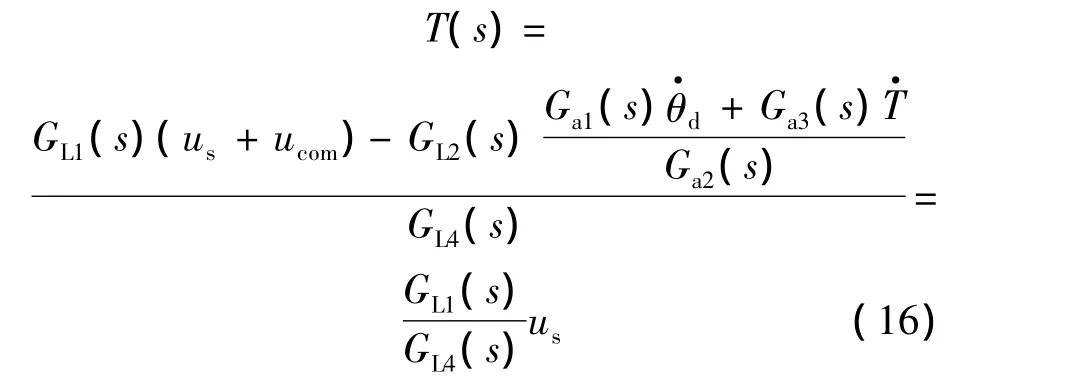
从式(16)可知,在同步补偿项ucom的作用下,理论上加载系统的输出力矩将不含舵机速度项,从而达到消除舵机运动扰动的目的.
为便于工程中应用,在加载系统和舵机的工作频率内式(14)中的补偿环节Gcom1和Gcom2可简化为
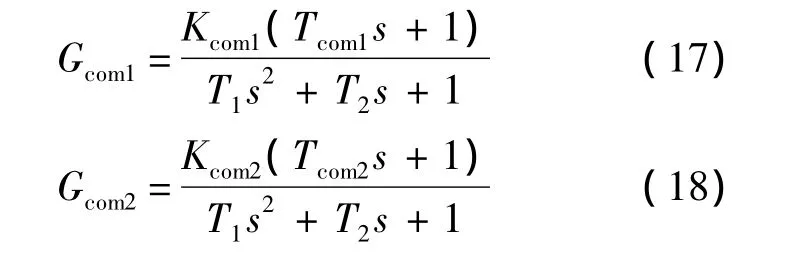
式中,Kcom1和 Kcom2为补偿环节的增益;T1,T2,Tcom1和Tcom2为补偿环节中的时间常数.
不同于传统的速度同步补偿方法,本文提出的同步补偿算法包含的舵机速度指令和加载系统的力矩微分信号.这说明:在消除舵机速度扰动的过程中,该算法考虑加载系统输出力矩对舵机速度输出的影响,故该算法在加载系统大力矩跟踪工况下具有更好的同步补偿能力.
4 仿真验证
为验证本文提出的补偿控制器,针对几种典型工况,做了相应的仿真验证.其仿真工况的对比曲线可分为3种:①静止加载工况的对比曲线;②梯度加载工况的对比曲线;③舵机与负载模拟器工作于不同频率时的动态加载工况对比曲线.
本文采用3种控制策略进行仿真对比验证,第1种为无补偿的控制策略,加载系统只采用传统的闭环PID控制策略;第2种是在保留PID控制策略的基础上,采用传统的速度同步控制策略;第3种是在保留PID控制策略的基础上,采用本文提出的改进型速度同步控制策略.所有的PID控制器具有相同的控制参数.在MATLAB环境下利用Simulink工具进行仿真验证,以最大动态输出力矩为2300 N·m的某型电液负载模拟器为对象,采用上述数学模型及表1所示参数.
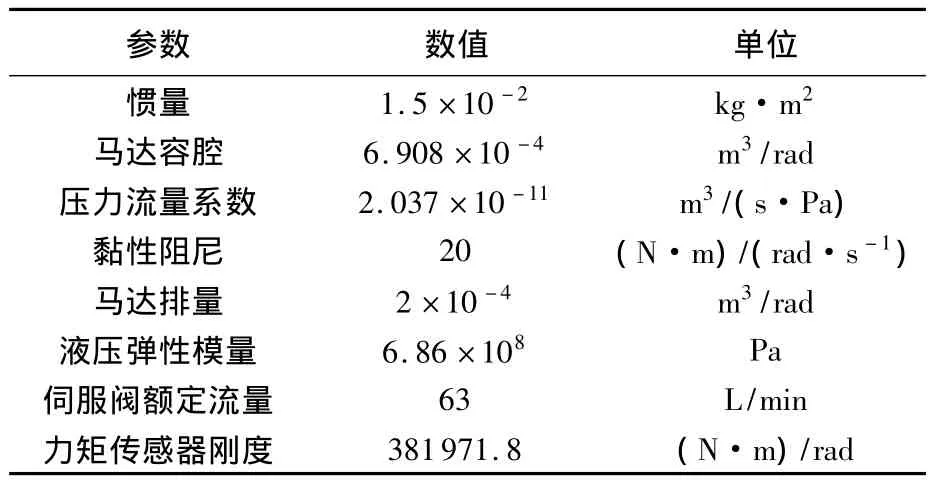
表1 仿真关键参数Table1 Key simulation parameters
4.1 静止加载对比曲线
舵机伺服系统做0°位置控制,负载模拟器跟踪1000 N·m、频率为2 Hz正弦力矩.3种控制策略对比仿真曲线如图5所示.
由仿真结果可知:改进型速度同步算法的最大跟踪误差只有约42.9 N·m,而传统PID控制和速度同步控制策略的最大跟踪误差约为46.1 N·m和87.6 N·m.
4.2 梯度加载对比曲线
梯度加载工况是加载系统的力矩指令与舵机实际输出角度为给定的比例关系的加载测试工况.图6所示为舵机做5°~3 Hz正弦位置跟踪,负载模拟器跟踪梯度为200 N·m/(°)时,3种控制策略的对比仿真曲线.仿真结果表明改进型速度同步算法的最大跟踪误差只有约41.7 N·m,而传统PID控制和速度同步控制策略的最大跟踪误差约为216 N·m和116 N·m.
4.3 不同频率下的加载跟踪对比曲线
为进一步验证改进型速度同步补偿控制策略,采用舵机伺服系统与加载系统在不同频率下的跟踪曲线进行验证.加载系统跟踪幅值为500 N·m、频率为5 Hz的正弦指令,位置伺服系统做幅值为10°、频率为1 Hz的正弦运动,3种控制策略下的跟踪曲线如图7所示.
由图7的仿真结果可知:改进型速度同步算法的最大跟踪误差只有约34.5N·m,而传统PID控制和速度同步控制策略的最大跟踪误差约为100 N·m和67 N·m.
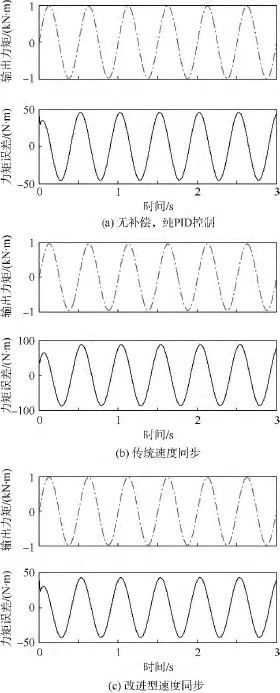
图5 静止加载下3种控制策略对比图Fig.5 Torque tracking in static loading situation

图6 梯度加载下3种控制策略对比图Fig.6 Torque tracking in gradient loading situation

图7 不同频率下加载跟踪的3种控制策略对比图Fig.7 Torque tracking in loading at different frequencies
上述仿真结果表明该补偿算法不仅有效消除舵机的运动干扰,而且提高加载系统的控制精度.
5 实验验证
5.1 实验设备描述
为验证提出的新型速度同步补偿控制器,搭建了实验平台,如图8所示.

图8 负载模拟器实验平台Fig.8 Experimental platform of load simulator
实验台由基座、加载通道(由液压马达、力矩传感器、角位移传感器、伺服阀和联轴器等构成)、舵机模拟通道、液压能源系统和控制系统组成.以最大动态输出力矩为6 kN·m的某型电液负载模拟器为实验对象.在图8中,左边的阀控马达系统为用于模拟舵机运动的位控系统,此系统用于提供该实验中的运动干扰,右边的阀控马达系统为力矩加载系统.计算机控制系统采用上下位机来实现.其上位机为综合管理子系统,实现系统监控功能,采用LabWindows/CVI编写.下位机为实时控制软件,采用微软公司的Visual Studio 2005和Ardence公司的RTX 7.0编写.采样周期为1 ms.
搭建的系统的主要元件规格说明如表2所示.
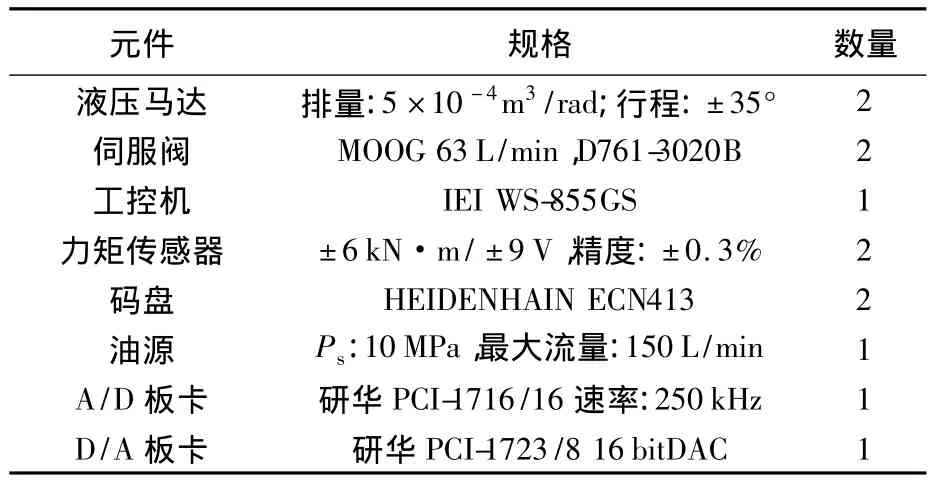
表2 实验台主要元件Table2 Main components of the test system
5.2 实验对比曲线
在实验验证中,仍对本文第4节提到的3种控制策略进行对比分析,所有的PID控制器均采用相同的控制参数.加载系统跟踪幅值为3kN·m、频率为0.5Hz的正弦指令,位置伺服系统做幅值为5°、频率为0.8 Hz的正弦运动,该工况下3种控制策略下的动态跟踪曲线如图9~图11所示.
由实验结果可知:PID控制和传统速度同步控制策略的最大跟踪误差约为522 N·m和320 N·m,而改进型速度同步算法的最大跟踪误差只有约232 N·m.
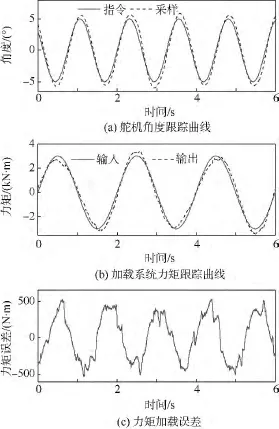
图9 传统PID控制器跟踪曲线Fig.9 No compensation,only PID controller
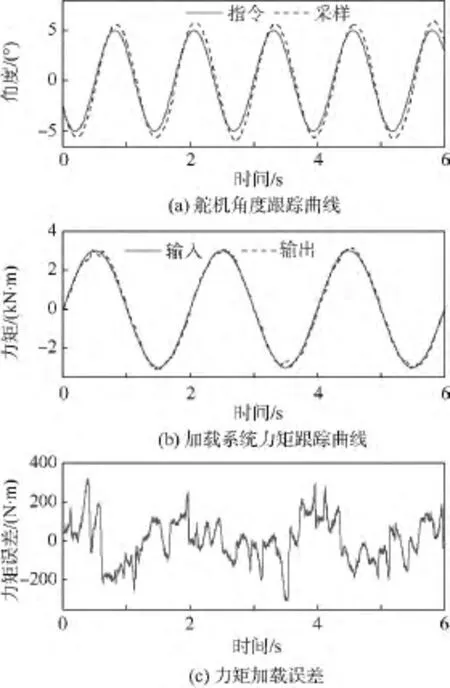
图10 传统速度同步控制方法Fig.10 Traditional velocity synchronizing controller

图11 改进型速度同步控制方法Fig.11 Improved velocity synchronizing controller
实验说明该改进型算法能充分利用舵机速度指令信号及负载模拟器力矩反馈信号进行干扰补偿.该补偿算法不仅有效增强加载系统的抗干扰能力,而且能提高系统的加载精度.
6 结论
本文针对电液负载模拟器加载时存在舵机速度干扰这一主要技术难点,对加载系统及舵机建模进行详细的理论分析推导,在目前常用的结构不变性方法和速度同步算法的基础上,提出了改进型速度同步补偿策略.该策略具有如下特点:
1)尤其适用于部分一体化舵机无法提供舵机电流或舵机电流噪声过大的实际测试工况.该工况下,基于舵机电流的传统速度方法无法实现.而本文提出基于舵机速度指令前馈的速度同步补偿方法,只需要舵机速度指令信号,不依赖舵机电流信号,亦不依赖舵机的角度、速度及加速度等传感器信号,更容易在工程上应用.
2)提出了利用舵机速度指令信号与加载系统力矩微分信号来在线预估舵机速度并进行速度同步补偿.相对于传统的速度同步算法,由于考虑加载力矩对舵机输出速度的影响(即舵机带载刚度),能更好地实现舵机速度估计,进而实现更优的同步补偿效果.
3)在典型工况条件下的仿真与实验结果表明,该控制器能有效消除来自舵机的运动扰动,并具有良好的动态力矩跟踪能力.
4)电液负载模拟器作为典型的机电液设备,该策略亦对其他同步补偿控制的机电液设备具备一定的参考意义.
References)
[1] 华清.电液负载模拟器关键技术的研究[D].北京:北京航空航天大学,2001:65-74.Hua Q.Studies on the key technology of electro-hydraulic load simulator[D].Beijing:Beijing University of Aeronautics and Astronautics,2001:65-74(in Chinese).
[2] 王巍,李雄峰,张新华,等.机械式反操作负载模拟器优化设计与仿真[J].北京航空航天大学学报,2011,37(2):161-166.Wang W,Li X F,Zhang X H,et al.Design optimization and simulation of mechanical anti-load simulator[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(2):161-166(in Chinese).
[3] Han S S,Jiao Z X,Yao J Y,et al.Compound velocity-synchronizing control strategy for electro-hydraulic load simulator and its engineering applications[J].Journal of Dynamic Systems,Measurement,and Control,2014,136(5):0510021-3.
[4] 牛国臣,王巍,魏志强,等.基于力矩前馈和舵机角度补偿的力矩控制[J].北京航空航天大学学报,2013,39(3):300-304.Niu G C,Wang W,Wei Z Q,et al.Torque control based on torque feedforward and rudder angle compensation[J].Journal of Beijing UniversityofAeronauticsand Astronautics,2013,39(3):300-304(in Chinese).
[5] 魏琼,吴帅,焦宗夏,等.高速运动舵机的气动伺服加载特性研究[J].航空学报,2013,34(8):1778-1785.Wei Q,Wu S,Jiao Z X,et al.Study on the pneumatic servo loading characteristics of high-speed motion actuators[J].Acta Aeronautica et Astronautica Sinica,2013,34(8):1778-1785(in Chinese).
[6] 刘长年.液压伺服系统优化设计理论[M].北京:冶金工业出版社,1989:121-123.Liu C N.Hydraulic servo system optimization design theory[M].Beijing:Press of Metallurgy Industry,1989:121-123(in Chinese).
[7] 王经甫,叶正茂,李洪人.双阀并联控制在船舶舵机电液负载模拟器多余力抑制中的研究[J].机械工程学报,2005,41(4):229-234.Wang J F,Ye Z M,Li H R.Study on eliminating the superfluous force of marine electro-hydraulic load simulator applied with dual-valve parallel connected control[J].Chinese Journal of Mechanical Engineering,2005,41(4):229-234(in Chinese).
[8] 李运华,焦宗夏,王占林,等.舵机力矩负载模拟器的混合控制方法研究[J].航空学报,1998,19(增):60-64.Li Y H,Jiao Z X,Wang Z L,et al.Research on hybrid control method of momental load simulator of actuator[J].Acta Aeronautica et Astronautica Sinica,1998,19(S):60-64(in Chinese).
[9] 于慈远,于湘珍,刘庆和,等.轴系刚度对新型空气动力负载模拟器的影响[J].航空学报,2001,22(2):148-151.Yu C Y,Yu X Z,Liu Q H,et al.Effects of shafting stiffness on new air dynamical load simulator[J].Acta Aeronautica et Astronautica Sinica,2001,22(2):148-151(in Chinese).
[10] Li Y H.Development of hybrid control of electro-hydraulic torque load simulator[J].Journal of Dynamic Systems Measurement and Control,2002,7124(1):415-419.
[11] Jiao Z X,Gao J X,Hua Q,et al.The velocity synchronizing control on the electro-hydraulic load simulator[J].Chinese Journal of Aeronautics,2004,17(1):39-46.
[12] Yao J Y,Jiao Z X,Shang Y X,et al.Adaptive nonlinear optimal compensation control for electro-hydraulic load simulator[J].Chinese Journal of Aeronautics,2010,23(6):720-733.
[13] Yao J Y,Jiao Z X,Yao B,et al.Nonlinear adaptive robust force control of hydraulic load simulator[J].Chinese Journal of Aeronautics,2012,25(5):766-775.
[14] Yoonsu N.QFT force loop design for the aerodynamic load simulator[J].IEEE Transaction on Aerospace and Electronic Systems,2001,37(4):1384-1392.
[15] 刘国建,李运华,郑琦,等.直升机桨距调节助力器电液加载系统的 H∞控制[J].北京航空航天大学学报,2011,37(2):140-146.Liu G J,Li Y H,Zheng Q,et al.Application of H∞theory in electro-hydraulic loading system of helicopter pitch adjusting booster[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(2):140-146(in Chinese).
[16] 李阁强,赵克定,袁锐波,等.μ理论在电液负载模拟器中的应用[J].航空学报,2007,28(1):228-233.Li G Q,Zhao K D,Yuan R B,et al.Application of μ theory in electro-hydraulic load simulator[J].Acta Aeronautica et Astronautica Sinica,2007,28(1):228-233(in Chinese).
[17] 姚建勇,焦宗夏.改进型LuGre模型的负载模拟器摩擦补偿[J].北京航空航天大学学报,2010,36(3):812-815.Yao J Y,Jiao Z X.Friction compensation for hydraulic load simulator based on improved LuGre friction model[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(3):812-815(in Chinese).
[18] Yao J Y,Jiao Z X,Yao B.Robust control for static loading of electro-hydraulic load simulator with friction compensation[J].Chinese Journal of Aeronautics,2012,25(6):954-962.
[19] 王春行.液压控制系统[M].北京:机械工业出版社,1998:41-43.Wang C X.Hydraulic control system[M].Beijing:China Machine Press,1998:41-43(in Chinese).
