基于产业相关性与时间序列模型的中国快递业务规模研究

孙 硕， 宋 妙， 陈 川 （同济大学 交通运输工程学院， 上海201804）

SUN Shuo, SONG Miao, CHEN Chuan (School of Transportation Engineering, Tongji University, Shanghai 201804, China)

0 引 言

近年来， 随着电子商务等的迅猛发展， 我国快递产业也进入了高速增长阶段。 数据显示， 2007～2011 年， 我国快递业务收入年复合增长率为21.96%， 2011～2014 年， 我国快递业务收入年复合增长率为39.2%[1]。 2014 年5 月， 据国家邮政局发展研究中心与德勤发布的《 中国快递行业发展报告（2014）》 预测， 2015 年中国快递市场行业规模将达2 800 亿元人民币， 2013～2015年中国快递市场年均复合增长率将在39.4%左右[2]。

快递业务的发展越来越受到社会各界的重视， 而快递业务规模的预测研究也有着极其重要的意义。 一方面， 科学合理的预测能够为决策者提供规划依据， 从而合理布局基础设施， 促进物流与交通的协调发展； 另一方面， 预测结果可以为快递产业界提供参考， 从而加深其对于快递市场规模和发展趋势的认识， 促进快递产业界的良性发展， 以更好地符合经济和社会发展的需要， 满足人民的物质文化需求。

为此， 学者们也对快递业务发展趋势和需求量的预测作了不少研究。 王莲花运用GM （1,1）模型来模拟我国快递行业的总收入， 并对未来几年的中国快递收入进行了预测， 检验结果表明GM （1,1）模型能够很好地模拟中国快递行业收入数据， 而且具有较高的模拟精度[3-4]。 张仲斐等选择ARIMA （1,1,1 ）（1,1,1 ）4作为模型， 利用四大快递公司的季度跨国快递包裹量， 对全球跨国快递业务量进行了预测[5]。 王天保等利用近年来全国快递运送量， 采用一次移动平均法和二次移动平均法对2016 年快递运送量进行了预测[6]。 吴传岭等引入二级多要素CES 生产函数， 利用邮政快递业从业人员数量、 地区资产形成规模和地区人均消费水平三个生产要素分别分析了中国快递业务数量和收入规模的贡献与要素的替代弹性， 结果显示中国快递业的形成主要受到消费水平的拉动[7]。

快递需求规模的发展变化一方面有其自身的规律， 会按一定的趋势变化， 因此， 可以利用自身的时间序列数据来总结变化的特点， 进而推测未来的发展变化； 另一方面， 快递需求规模与地区的经济社会发展水平等息息相关， 双方具有极高的相关性与依存性， 而经济与社会发展的规律性相对更强， 更容易对其进行更为可靠的预测， 故可以利用二者的相关性， 通过经济与社会发展相关联要素的预测来推测快递需求的变化情况。 因此， 本文以全国快递业务收入表征全国快递业务规模， 基于快递产业的相关性而建立了多元逐步回归模型， 基于快递业自身时间序列数据而建立了灰色预测模型和多项式回归分析模型， 通过对三种预测模型结果的综合加权来得到最终的规模预测值， 以期为行业发展提供可靠的理论依据和参考。

1 多元逐步回归模型

由于经济与社会发展要素一般具有较强的规律性， 相较快递发展而言易于预测， 因此， 可利用多元逐步回归模型， 分析其与快递业的关联性， 以找出对快递业发展显著相关的要素， 实现对未来快递业务规模的预测。

1.1 多元逐步回归模型基本原理与计算步骤[8]

在实际问题中， 人们总是希望从对因变量有影响的诸多变量中选择一些变量作为自变量， 应用多元回归分析的方法建立“ 最优” 回归方程以便对因变量进行预报或控制。 所谓“ 最优” 回归方程， 主要是指期望在回归方程中包含所有对因变量影响显著的自变量而不包含对影响不显著的自变量的回归方程。 逐步回归分析正是根据这种原则提出来的一种回归分析方法。 它的主要思路是在考虑的全部自变量中按其作用大小， 显著程度大小或者贡献大小， 由大到小地逐个引入回归方程， 而那些作用不显著的变量可能始终不被引入回归方程。 另外， 己被引入回归方程的变量在引入新变量后也可能失去重要性， 而需要从回归方程中剔除出去。 引入一个变量或者从回归方程中剔除一个变量都称为逐步回归的一步， 每一步都要进行检验， 以保证在引入新变量前回归方程中只含有对影响显著的变量， 而不显著的变量已被剔除， 其主要计算步骤如下：

（1） 确定F检验值

在进行逐步回归计算前要确定检验每个变量是否显著的F检验水平， 以作为引入或剔除变量的标准。F检验水平要根据具体问题的实际情况来定。 一般地， 为使最终的回归方程中包含较多的变量，F水平不宜取得过高, 即显著水平α 不宜太小。F水平还与自由度有关， 因为在逐步回归过程中， 回归方程中所含的变量的个数不断在变化， 因此方差分析中的剩余自由度也总在变化， 为方便起见， 常按n-k-1 计算自由度。n为原始数据观测组数，k为可能选入回归方程的变量个数。 例如n=15， 估计可能有2～3 个变量选入回归方程， 因此取自由度为15-3-1=11， 查F分布表， 当α=0.1， 自由度f1=1，f2=11 时， 临界值Fα=3.23， 并且在引入变量时， 自由度取f1=1，f2=n-k-2，F检验的临界值记F1， 在剔除变量时自由度取f1=1，f2=n-k-1，F检验的临界值记F2， 并要求F1≥F2， 在实际应用中可取F1=F2。

（2） 逐步计算

如果已计算t步（包含t=0） ， 且回归方程中已引入l个变量， 则第t+1 步的计算为：

①计算全部自变量的贡献V'（偏回归平方和） 。

②在已引入的自变量中， 检查是否有需要剔除的不显著变量。 这就要在已引入的变量中选取具有最小V'值的一个， 并计算其F值， 如果F≤F2， 表示该变量不显著， 应将其从回归方程中剔除， 计算转至③。 如F＞F2则不需要剔除变量， 这时则考虑从未引入的变量中选出具有最大V'值的一个并计算F值， 如果F＞F1， 则表示该变量显著， 应将其引入回归方程， 计算转至③。如果F≤F1， 表示已无变量可选入方程， 则逐步计算阶段结束， 计算转入③。

③剔除或引入一个变量后， 相关系数矩阵进行消去变换， 第t+1 步计算结束。 其后重复①～③再进行下一步计算。

由上所述， 逐步计算的每一步总是先考虑剔除变量， 仅当无剔除时才考虑引入变量。 实际计算时， 开头几步可能都是引入变量， 其后的某几步也可能相继地剔除几个变量。 当方程中已无变量可剔除， 且又无变量可引入方程时， 第二阶段逐步计算即告结束， 这时转入第三阶段。

（3） 其他计算

主要是计算回归方程入选变量的系数、 复相关系数及残差等统计量。

1.2 建模与预测过程

借鉴国家邮政总局与德勤发布的《 中国快递行业发展报告2014》 中对中国快递服务市场发展驱动力的分析成果， 以全国快递业务收入为因变量y， 选取经济与社会两大类共21 个相关联指标要素作为自变量进行建模， 如表1 所示。

查询国家统计局、 相关部委及中国电子商务研究中心等网站， 得到2007～2013 年数据（2014 年部分数据尚未更新） ， 利用MATLAB 进行逐步回归建模。 模型分析结果如表2、 表3 和图1 所示。

根据模型检验结果得出结论： 剩余标准差较小， 决定系数及调整后的决定系数均为1， 表示回归方程对于快递业务收入的解释性良好。 回归方程的显著性检验（即F检验） 方面，F值为2.73154+E6， 数值较大， 且伴随概率p＜0.001， 说明自变量造成的因变量的变动远远大于随机要素对因变量造成的影响， 方程总体线性关系显著。 变量的显著性检验方面， 各参数t统计量的伴随概率均通过了0.05 的显著性检验， 拟合效果显著。

模型结果显示， 对y影响显著的变量分别为：x4全国网上零售额（亿元） 、x7全国B2B 市场交易规模（万亿元） 、x13货运周转量（亿吨公里） 、x17居民消费水平（元） 、x21互联网上网人数（亿人） 。 回归方程如下：

其中：y——全国快递业务收入（亿元） ；x4——全国网上零售额（亿元） ；x7——全国B2B 市场交易规模（万亿元） ；x13——货运周转量（亿吨公里） ；x17——居民消费水平（元） ；x21——互联网上网人数（亿人） 。

由于短期内网上零售额、 B2B 市场交易规模、 居民消费水平等的发展趋势规律性较强， 故可采用多元回归分析对2020 年的值进行简便预测。 预测结果如表4 所示。

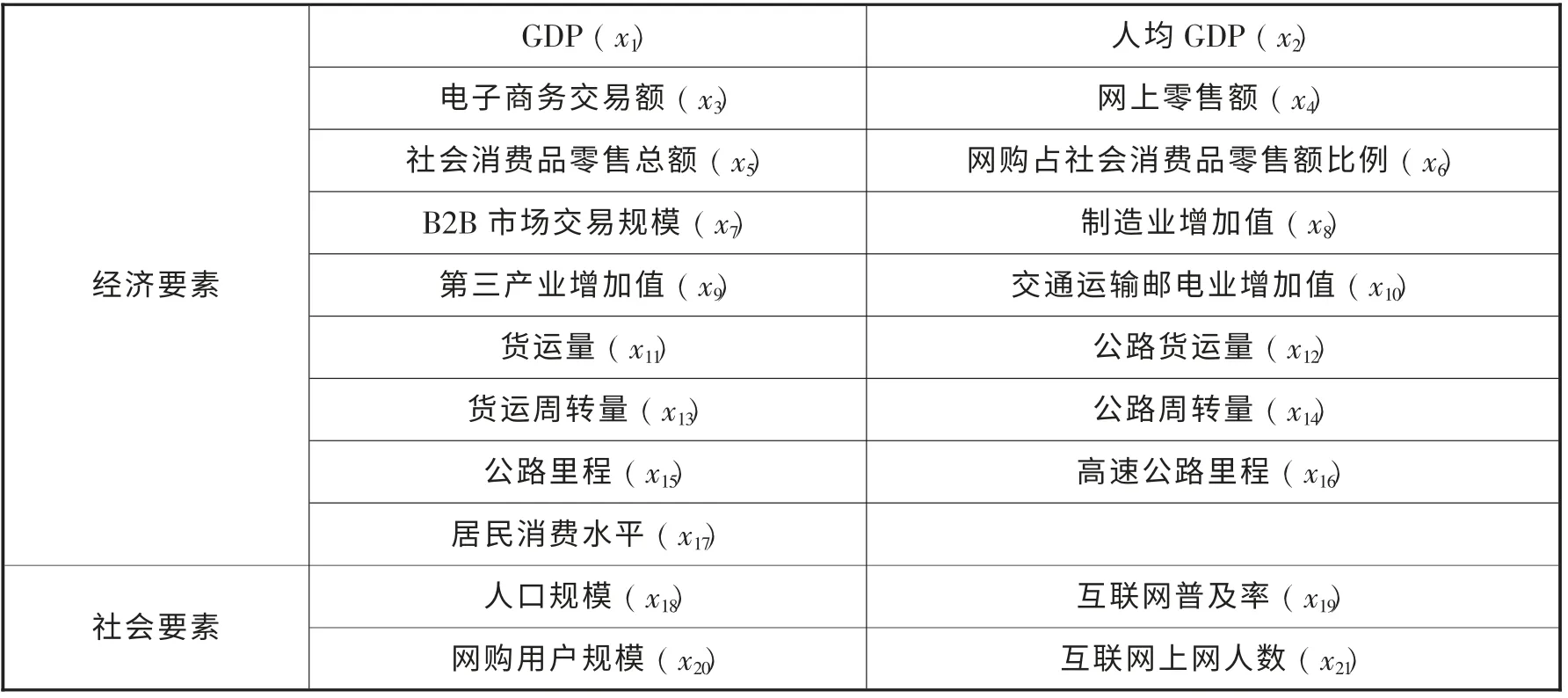
表1 快递行业相关自变量列表

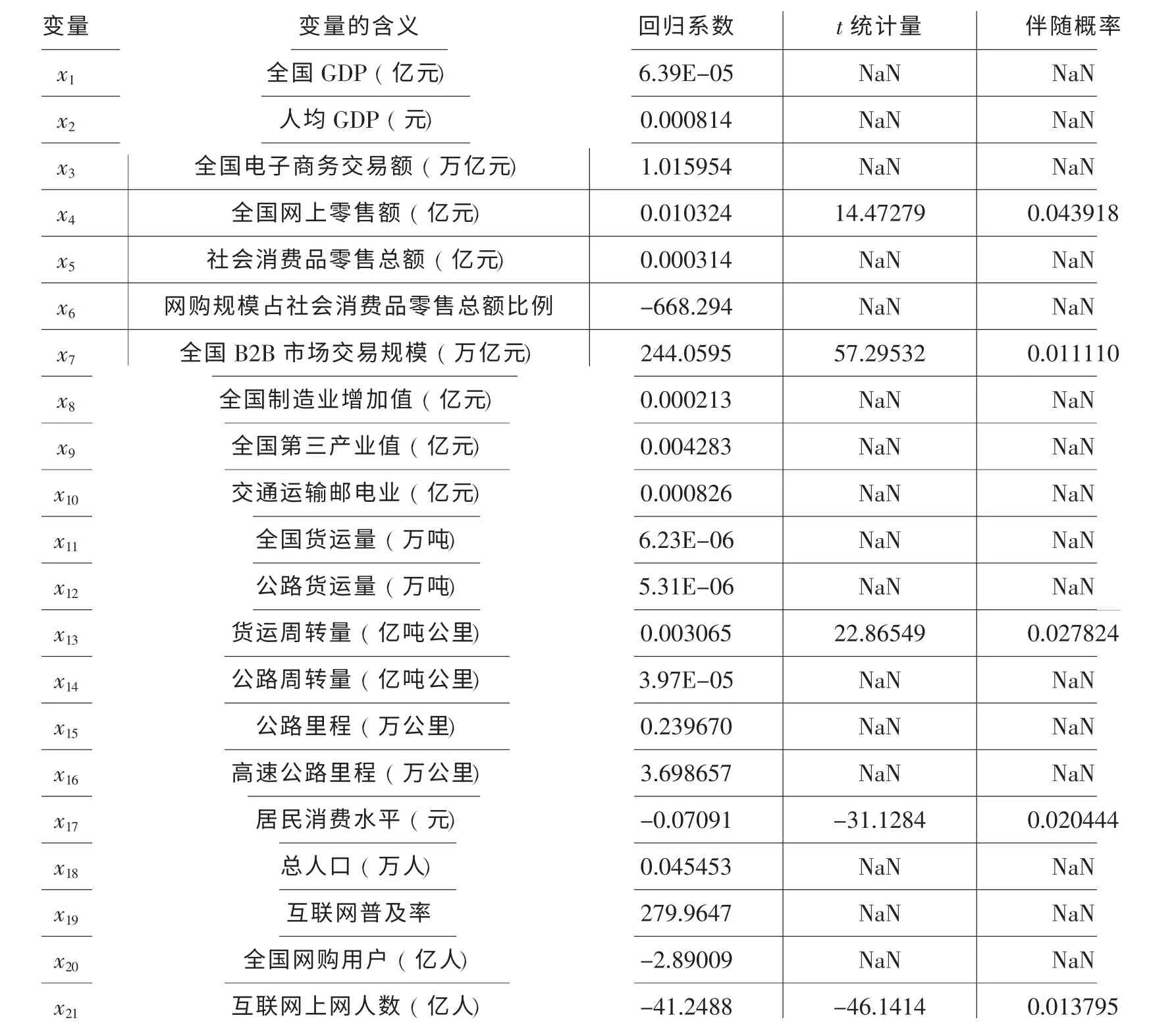
表2 模型参数回归系数结果

表3 模型检验结果

根据表4 结果， 利用逐步回归方程计算可得2020 年全国快递业务收入为10 521.5 亿元。

2 灰色预测模型

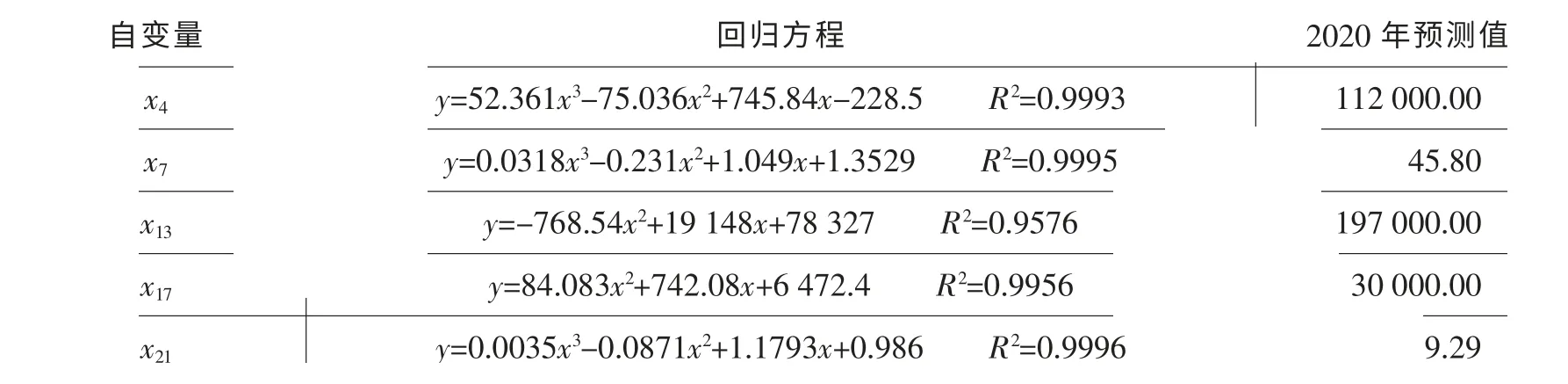
表4 2020 年相关变量回归预测结果

灰色系统理论是基于关联空间、 光滑离散函数等概念定义灰导数与灰微分方程， 进而利用离散数据建立微分方程形式的动态模型， 由于这是表征灰色系统的基本模型， 它是近似的、 非唯一的， 称为灰色模型（GM） 。 其基本过程如下：

由历史数据， 计算每年的总和， 记为：

α 为确定参数， 得到GM （1,1）的白化微分方程模型为：

其中参数由灰微分方程（4） 确定：

于是方程（3） 有响应（特解） ：

故相应的有：

根据灰色预测原理， 以2007 年为起始年， 2007～2014 年全国快递收入为依据数据， 利用MATLAB 建立灰色预测模型GM （1,1），对2020 年全国快递收入进行预测。 模型的后验差比（均方差比值）C为0.10117， 小于0.35， 小误差概率P为1， 大于0.95， 说明此模型精度等级为1 级（好） 。 根据模型得出， 2020 年， 全国快递业务收入约为11 355.9 亿元（软件输出趋势如图2 所示） 。

3 多项式回归分析模型

设x1,x2,…,xm为系统的相关因素， 对这些相关因素若有n次观测得到的样本数据为则系统相关因素的相关矩阵为

根据回归分析原理， 以2007 年为起始年， 2007～2014 年全国快递业务收入为基础数据， 利用Excel 作快递业务收入变化关系的拟合分析， 拟合结果显示回归拟合方程的确定性系数为0.9997， 说明拟合结果可靠性很高， 回归模型对快递业务收入的预测性能良好， 结果如图3 所示。

其回归方程为：y=53 756x3-127 557x2+677 022x+3 000 000

根据快递业务收入发展趋势的计算公式， 可得：

2020 年：y2020=10 834.6 亿元， 即2020 年， 全国快递业务收入将达10 834.6 亿元左右。

汇总以上三种模型结果， 整理如表5 所示。

综合三种模型预测结果， 取平均值得2020 年， 我国快递业务收入将达10 900 亿元左右。

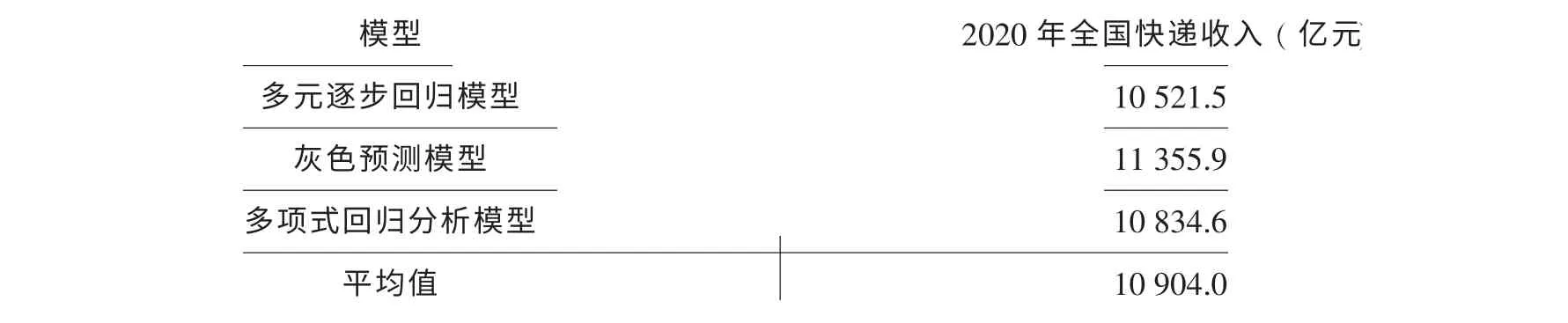
表5 全国快递业务收入预测结果汇总

4 结束语

本文从快递产业的经济社会相关性及其自身发展特点两个方面， 分别建立了多元逐步回归、 灰色预测和多项式回归分析模型， 检验结果表明模型具有较高的精度， 而三个模型预测结果间最大仅相差7.9%， 这也从侧面验证了结果的可靠性。

综合三个模型结果， 预测我国2020 年快递业务收入将达10 900 亿元左右， 我国快递业在未来几年将继续保持中高速的增长趋势。 其次， 通过多元逐步回归模型的关联性分析显示， 全国网上零售额、 B2B 市场交易额、 货运周转量、 居民消费水平及互联网上网人数等5 个指标对快递业务规模影响显著， 表明这5 个指标与快递产业发展息息相关。

[1] 国家邮政局. 2014 年邮政行业发展统计公报[EB/OL]. (2015-04-29)[2015-06-25]. http://www.spb.gov.cn/dtxx_15079/201504/t20150429_462010.html.

[2] 国家邮政局发展研究中心， 德勤. 中国快递行业发展报告（2014）[Z]. 2014.

[3] 王莲花. 基于GM （1,1）模型的中国快递行业收入预测分析[J]. 物流技术， 2012,31(2):84-86.

[4] 王莲花. 我国快递行业季度业务收入预测模型及分析[J]. 物流技术， 2014(6):144-146.

[5] 张仲斐， 赵一飞. 基于ARIMA 模型的全球跨国快递业务量预测[J]. 华东交通大学学报， 2012,29(1):102-107.

[6] 王天保， 张玉军， 武传胜,等. 移动平均法在快递预测上的研究[J]. 东方教育， 2014(11):177,315.

[7] 吴传岭， 施国洪. 基于二级多要素CES 生产函数的快递业务规模研究[J]. 统计与决策， 2010(13):72-74.

[8] 徐群. 非线性回归分析的方法研究[D]. 合肥： 合肥工业大学（硕士学位论文） ， 2009.