半定规划上一种有效的内点法

田文娟

(西安电子科技大学数学与统计学院，陕西西安 710126)

自从Karmarkar's algorithm［1］被证明具有多项式的有效性后，多项式就被作为衡量算法有效性的重要指标。所以，众多的内点算法被形成，尤其是半定规划的内点算法。由于其在众多领域均有着广泛和重要的应用，如经济、管理、工程设计、控制、交通等部门［2－5］。故受到了更多重视。而文中在求解半定规划的优化问题时，也需考虑其的多项式有效性，而多项式有效性与中心参数及步长有一定的关系。但长久以来，中心参数始终是固定的，且与步长独立。本文提出了半定规划中基于宽邻域的可行内点算法，且中心参数与步长有多项式的关系，在每一次迭代中，中心参数和步长均是使对偶间隙降到最小的一组最优解，收敛性也较好。

1 问题背景

考虑半定规划问题(P)及其对偶问题(D)

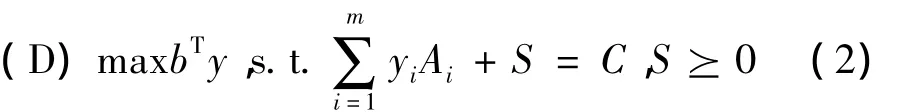
定义宽邻域N－∞(1－θ):={(X，y，S)∈F0∶λmin(XS)≥θμ}。半定规划(P)和(D)等价于求解最优性条件(KKT条件)

考虑式(3)的扰动方程

由于X，S∈Sn，乘积 XS未必属于Sn。所以，提出相似对称化算子Hp

对等式系统应用牛顿法，可得方程组

定义新的迭代为

其中，α∈［0，1］，σ∈［0，1］。

若 P 满足 P XS P－1∈Sn，则对于(X，y，S)∈Sn++××Sn++，系统式(6)有唯一解。

本文限制尺度矩阵P满足

而令式(8)中第三方程的右端项为μI，系统方程组为

则

引理1邻域N－∞(1－θ)是缩放不变的，即(X，y，S)∈N－∞(1－θ)当且仅当，(X^(α，σ)，y(α，σ)，S^(α，σ))包含于相应的变尺度邻域。证明与文献［9］中命题4.1相似。

引理2 设(ΔX(σ)，Δy(σ)，ΔS(σ))被定义在式(5)中，以下成立

定理1 从式(9)可知，以下关系成立

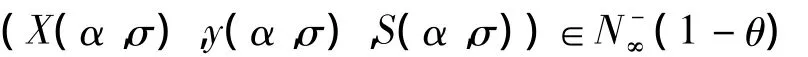
令

由式(10)表明，f(α，σ)对于α是一个单调递增的函数。因此，对于任何固定的σ∈［0，1］，若对于最大的，有 f(α，σ)≤0成立，则对于任何 α∈(0，α］有 f(α，σ)≤0 成立。从而，λmin(X(α，σ)S(α，σ))≥θμ(α)＞0 成立，由文献［9］中引理可知，X(α，σ)≥0，S(α，σ)≥0成立。

设(X0，y0，S0)∈F0，在每次迭代中，若要对偶间隙μ(α，σ)最小，且满足(X(α，σ)，y(α，σ)，S(α，σ))∈F，则有以下最优问题

优化问题式(11)的解法类似于文献［10］中(18)的解法。

情况1 α =1，f(1，σ)=0，如 f(1，σ)=0 有解，则其最小解可能是式(11)的最优解。

情况2 α≠1时，可知 f(α，σ)=0，h(σ):=(a2+a1)σ2+2a0σ －a0=0。

综上所述，在情况 1，2 中，对于(α，σ)∈(0，1］× (0，1)，将用以上方法求出的可能最优解对(α，σ)代入式(11)的目标函数中，使得μ(1－α(1－α))最小，便是要找的最优解对(α，σ)。

2 算法及其复杂性

输入参数 Ai，θ∈(0，1)，ε ＞ 0，初始点(X0，y0，S0)，且其满足(X0，y0，S0)∈N－∞(1－θ)。计算，令k:=0。

步骤1 若〈Xk，Sk〉≤ε，则停止。

步骤 3 根据定理 1，2 计算 px，qx，ps，qs，p1，q1，r1，p2，q2，r2，a0，a1，a2。

步骤4 下面选择α，σ。

(1)若 a0=0，令 σ =0，α =1。

(2)若 a0＞0。

1)解方程 f(1，σ)=0，若 f(1，σ)在 σ∈(0，1)有解，则解对(α，σ)=(1，σ)可能是式(11)的最优解。

2)解方程组 h(σ)=0，f(α，σ)=0，从而，求的解对(α，σ)∈(0，1)×(0，1)可能是式(11)的最优解。

3)将1)，2)中的可能最优解对(α，σ)代入式(11)的目标函数中，使得μ(1－α(1－σ))最小，即是所要找的最优解对(α，σ)。

步骤 5 令(Xk+1，yk+1，Sk+1)=(X(α，σ)，y(α，σ)，S(α，σ))令 k:=k+1，转步骤1。

证明 由μ(α)=μ(1－α(1－α))得(1－α(1－

而log(1－α(1－σ))≤ －α(1－σ)＜0，所以，只需满足成立即可。因此，k≥时，迭代终止。

推论1 在算法多项式的证明中，为使宽领域N∞－(1－θ):={(X，y，S)∈F0∶λmin(XS)≥θμ}成立。取 α=1，σ=1－，文献［11］满足。此时，其复杂性为O()与步骤4中1)的效果一致，且明显不如本文算法。若取α＜1，由于每次迭代的步长变小，对偶间隙趋于零的速度变慢，其的复杂性将不及O)。因此，与本文每次迭代均取(α，σ)的最优解相比，其需要更多的时间，故验证了所提算法更优。

［1］Karmarkar N.A new polynomial－ time algorithm for linear programming［J］.Combinatorica，1984(4):373 －395.

［2］Kojima M，Mizuno S，Yoshise A.A polynomial－ time algorithm for a class of linear complementarity problem ［J］.Math Program，1989，44(1 －3):1 －26.

［3］Mizuno S，Todd M Y.On adaptive step primal－ dual interior－ point algorithms for linear programming［J］.Math Operation Result，1993，18(4):964 －981.

［4］Salahi M，Mahdavi－ Amiri N.Polynomial time second order Mehrotra－ type predictor－ corrector algorithms［J］.Application Mathation Comput，2006，183(1):646 －658.

［5］Feng Z，Fang L.A wide neighborhood interior point method with iteration complexity bound for semidefinite programming［J］.Optimation，2010，59(8):1235 －1246.

［6］Nesterov Y，Todd M J.Self－ scaled barriers and interiorpoint methods for convex programming［J］.Math Operation Result，1997，22(1):1 －42.

［7］Nesterov Yu，Todd M J.Primal－ dual interior－ point methods for self－ scaled cones［J］.SIAM Journal Optimization，1998，8(2):324 －364.

［8］Monteiro R D C，Zhang Y.A unified analysis for a class of long－step primal－dual pathfollowing interior－point algorithms for semidenite programming ［J］.Manuscript，1996(11):670－681.

［9］刘长河.锥规划中若干内点算法的复杂性分析研究［D］.西安:西安电子科技大学，2012.

［10］Yang Y.An interior－point algorithm for linear optimization based on a new barrier function ［J］.Applied Mathematics and Computation，2011，25(3):1110 －1127.

［11］Wright S J.Primal－ dual interior－ point method［M］.NZ USA:Siam Press，1997.