基于非线性混合效应状态空间模型的粒子滤波

王 瑞

(西安电子科技大学数学与统计学院，陕西西安 710071)

非线性非高斯状态空间模型［1－3］的最优估计［4］在信号处理、金融、无线通讯等领域具有重要的应用。针对实际问题中出现的非线性非高斯模型，出现了一种被称为“序贯重要性采样(SIS)”的Monte Carlo方法，其通过离散的随机测度逼近概率分布。然而由于高度的计算复杂性和退化问题，1993年 Gordon提出了重采样概念，克服了早期算法的退化问题，出现了第一个可操作的Monte Carlo滤波器。现代计算技术使Monte Carlo滤波方法得到了迅速发展，现在通称为粒子滤波器［5］。本文是在非线性非高斯状态空间模型中假设某些参数未知，采用粒子滤波算法及改进后的辅助粒子滤波算法分别对状态进行估计。粒子滤波算法［6－8］源于 Monte Carlo［9－10］的思想，其核心思想是通过从后验概率中抽取的随机状态粒子来表达其分布，是一种顺序重要性采样法(Sequential Importance Sampling)。

本文介绍了非线性混合效应状态空间模型，粒子滤波算法相关的序贯重要性采样(SIS)及采样重要性重抽样(SIR)算法，并引入一种新的改进粒子滤波算法—辅助粒子滤波算法(APF)［11－12］，通过实例模型进行仿真，进一步说明了APF算法是可行的，且相比其他算法更加有效。

1 非线性混合效应状态空间模型

非线性状态空间模型是一种常用的动态系统模型，其主要有两部分

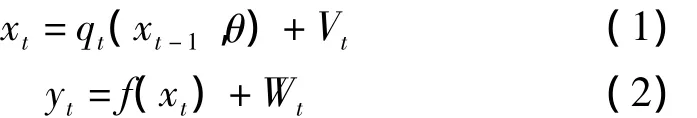
其中，θ是固定效应;bj是随机效应，服从均值为0，协方差为D的正态分布。文中 θ被当作未知参数，式(1)～式(3)被称为混合效应状态空间模型(NLMESSM)。这里研究的是单个目标，即当参数未知得到一个目标的观测信号值时，用序贯重要性采样和改进的辅助粒子滤波算法方法进行在线估计状态。

2 粒子滤波

序贯重要性采样算法是一种通过蒙特卡洛模拟实现贝叶斯滤波器的技术，其核心思想是利用一系列随机样本的加权和来表示所需后验概率密度，从而得到状态的估计值。

假设观测值y1∶t已知，所求的状态设为，状态的后验密度为，则状态估计的推导过程如下

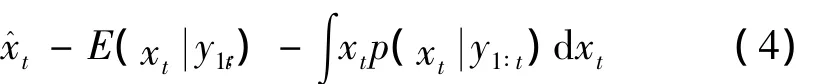
则

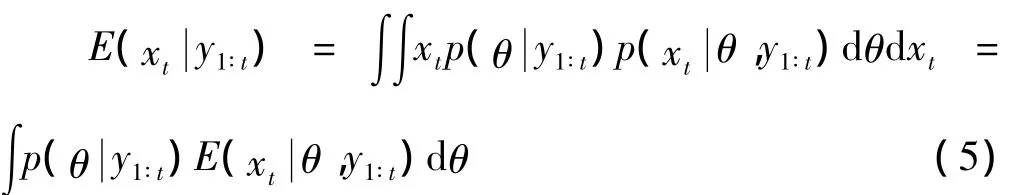
在初始时刻假定随机样本{θj}mj=1是从参数的先验分布p(θ)中抽取的，则在下一时刻，从样本中按照每个粒子对应的权重进行重采样得到新样本。以此类推，假设在t时刻，得到一组参数样本，这些样本近似服从参数的后验分布p(θ具体更新步骤如下:

(1)初始时刻从先验分布 p(θ)中抽取样本{θj}mj=1。

(3)按照权重wjt对样本{θj}mj=1进行重抽样，得到t+1时刻样本{θ*j}mj=1

因此，由式(5)可得

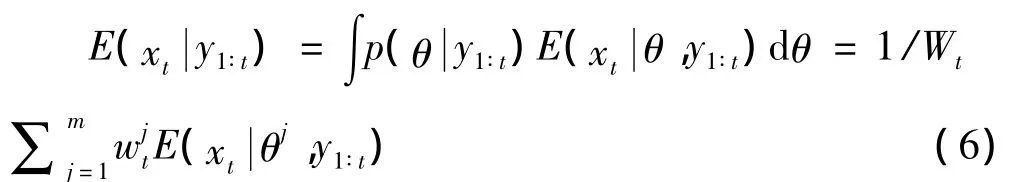
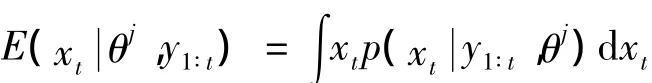
通过粒子滤波算法，用样本均值来近似这一期望。定义ωt为粒子的权重，则

假设在t时刻有状态变量的随机样本{xi}N，当ti=1参数θj和观测值yt+1为已知时，具体的更新步骤如下:(1)初始时从中得到样本 x*it+1，j=1，2，…，N。(2)计算每个样本对应的权重 ωit+1 ∝。标准化权重。(3)重采样则有

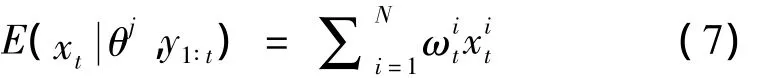
将式(7)代入式(6)可得

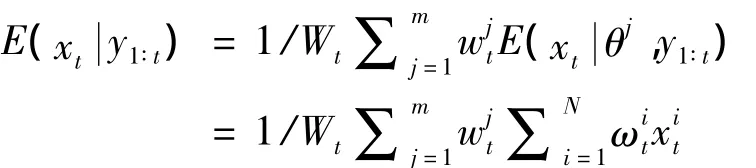
即得到了状态的估计值x^t。

3 辅助粒子滤波

以上采样重抽样(SIS)算法虽简单易求，便于抽样，但由于其仅从粒子运动和之前的一些状态盲目的进行抽样，因而可能会使大量的低权值粒子丢失，最终导致更高的蒙特卡洛且滤波性能更差。一个可行的提高性能方法就是使用辅助粒子滤波(APF)。其以SIS为基础，假设在t时刻，得到一组样本{xj，θj∶j=1，…，t t N}，及相对应的权重{ωjt∶j=1，…，N}。需注意的是，θ的下标t表示参数来自t时刻的后验密度，而并非随时间变化。有了t+1时刻的观测值yt+1，需从p(xt+1，y1∶t+1)中产生样本，则由贝叶斯理论可知

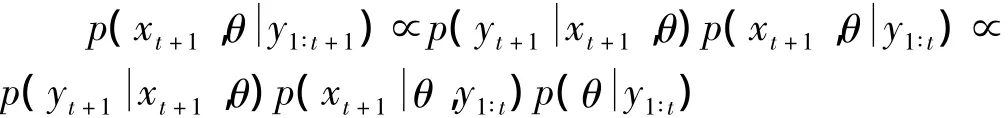
为了推导出参数和状态的联合滤波，明显要处理关于未知的密度函数p(θ的问题。

在t时刻，设已知后验参数样本θjt和权重 ωjt，j=1，…，N，用一种离散的蒙特卡洛来近似p()，记和Vt分别为蒙特卡洛后验密度p(θ)的均值和方差矩阵。则平滑核密度形式为N

步骤1 用{μjt+1，mjt}来确定{xt，θ}的先验点估计，j=1，…，N，其中可由状态方程计算得到，且

步骤2 按照概率权重gjt+1从集合{1，2，…，N}中抽取辅助整数变量，称为采样指数k，其中gjt+1∝ωjtp

步骤3 从第k个核密度的正态分量中抽取新的参数向量 θkt+1，即 θkt+1～N(·mkt，h2Vt)。

步骤6 多次重复步骤2～步骤5产生最终后验近似所需的{xkt+1，θkt+1}及权重 ωkt+1。

通过以上得到的一组状态样本及其权重，对这些样本进行加权平均就是此时刻所估计的状态，即

4 仿真

4.1 一维非线性追踪模型

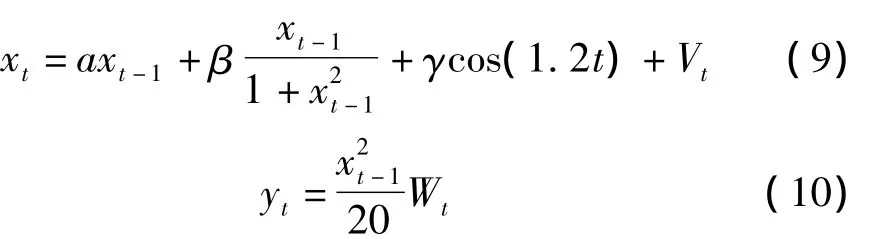
这两个模型被称为状态空间模型，其来自Andrade(1987)，是一类非线性追踪模型。这是一个关于目标跟踪的模型，假设研究对象为单个目标，要对此目标的状态进行估计。其中Vt～N(0，δ2v)，Wt～ N(0，δ2w)，定义时间长度 T=100，α =0.5，β =25，γ =8，δ2v=10，δ2w=1，这里需固定状态误差δ2v和观测误差δ2w，取状态方程中的参数α，β，γ作为未知参数，其中α，β，γ的分布为a ～N(0.5，0.03)，β ～ N(25，3)，γ ～ N(8，0.8)。令向量 θ=(α，β，γ)，则有混合效应模型 θj=α +bj，j=1，2，…，m。其中，固定效应θ=(0.5 25 8)，bj是随机效应，服从均值为0，协方差为D的正态分布。这里从初始状态分布N(0.1，2)中分别抽取N个粒子，从参数θ的先验分布中抽取M个参数。

在表1中，针对不同的状态和参数粒子数50，100，150，200，分别列出了SIR和APF在不同粒子个数时的均方根误差(RMS)，其中N为粒子个数。估计值与真实值的均方根误差为

表1 SIR与APF在粒子个数不同时各自的均方根误差

4.2 仿真结果分析

由表1可看出，通过SIR滤波计算得到的RMS比APF所得到的RMS要大，其中在N=50时，两种算法的RMS相差最大，随着粒子数N的增多，差距逐渐减小，这说明粒子数目的多少是影响仿真结果的一个因素，粒子数目越多，仿真效果越好。

在一维非线性追踪模型中，两种算法的时间长度tf=100，粒子个数N=200，参数个数M=200。SIR滤波仿真结果如图1所示，图中红线代表真实状态，绿线代表参数未知时的状态估计。可看出，两条曲线存在着差距，状态估计的波动范围远小于真实值，这可能是由于参数的重要性密度函数选择不合适，从而导致参数的样本远离真实值。APF滤波仿真结果如图2所示，从图中可看出，APF算法逼近真值程度明显更优，且状态估计结果与真实值之间相差较小，这是由于APF算法中对参数样本按照各自的权重重新选择参数的核密度，使得从核密度中产生的样本更加接近真实值，从而使权值变化幅度更小，计算得到的RMS则也较小。

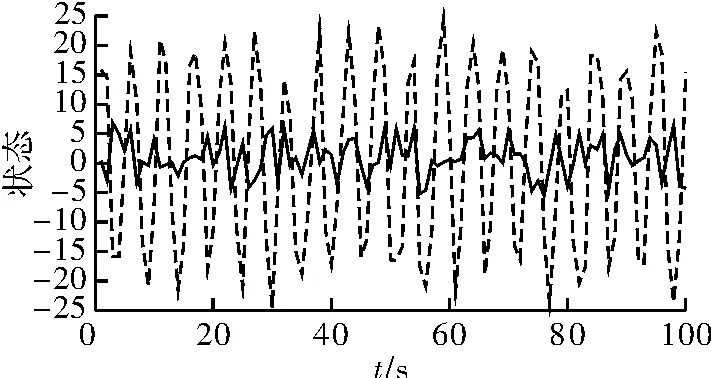
图1 真实状态及SIR估计状态与时间t的关系

图2 真实状态及APF估计状态与时间t的关系

5 结束语

基于混合效应状态空间模型，针对状态估计提出了SIR算法和APF算法。这两个算法各有利弊，如SIR滤波虽其先验分布函数简单易求，且易于抽样，但由于与外部观测值无关，因而产生的粒子大部分位于后验概率分布尾部，使得权值变化较大，仿真效果并不理想。而APF算法与外部观测信息有关，使得采样粒子更接近真实状态，但由于过程相对复杂，因此实时性比SIR稍微差。整体而言，APF滤波仍比SIR滤波有大幅的改进，故在处理此类问题中占有较大优势。

［1］赵昕东，耿鹏.基于Bayesian Gibbs Sampler的状态空间模型估计方法研究及其在中国潜在产出估计上的应用［J］.统计研究，2009，26(9):55 －63.

［2］钱伟民，柴根象.纵向数据混合效应模型的统计分析［J］.数学年刊，2004，25(4):445 －456.

［3］包云霞，鲁法明，刘福升.非线性状态空间模型的EHMM抽样法［J］.山东科技大学学报，2005，24(3):104 －106.

［4］侯代文，殷福亮.非线性系统中状态和参数联合估计的双重粒子滤波方法［J］.电子与信息学报，2008，30(9):2128－2133.

［5］杨小军，潘泉，王睿，等.粒子滤波进展与展望［J］.控制理论与应用，2006，23(2):261 －267

［6］刘维亭，戴晓强，朱志宇.基于重要性重采样粒子滤波器的机动目标跟踪方法［J］.江苏科技大学学报，2007，21(1):37－41.

［7］江宝安，卢焕章.粒子滤波器及其在目标跟踪中的应用［J］.雷达科学与技术，2003，1(3):170 －174.

［8］Sanjeev M，Arulam Palam，Simon Maskell，et al.A tutorial on particle filters for online nonlinear/non－gaussian bayesian tracking［J］.IEEE Transactions on Signal Processing，2002，50(2):174－188.

［9］李军科，张串，吴建军.基于蒙特卡洛方法的粒子滤波算法研究［J］.电脑与信息技术，2008，16(1):49 －53.

［10］李东风，谢衷洁.Monte Carlo滤波新进展及其应用［J］.数学进展，2004，33(4):415 －424.

［11］赵梅，张三同，朱刚.辅助粒子滤波算法及仿真举例［J］.北京交通大学学报，2006，30(2):24 －28.

［12］王洪有.基于辅助粒子滤波算法的红外目标跟踪［J］.应用光学，2010，31(1):132 －135.