基于FPGA的全相位FFT和相位推算法频率测量
2015-12-18程遥
程 遥
(西安电子科技大学电子工程学院,陕西西安 710071)
在现代战争中,数字接收机是电子侦察系统的重要组成部分,其目的在于确定敌方辐射源的存在与否,并测定其各种特征参数。在各种特征参数中,频率反映了雷达的功能和用途,是信号分选和威胁识别的重要参数之一[1]。因此,频率测量的精度和瞬时性就显得尤为重要。在实际战场环境下,信号往往伴随着较强的噪声,所以频率测量系统还应具有较好的抗噪性能。
在对测频精度和瞬时性要求高的测频系统中,理论上可以采用相位推算法[2],该方法先将信号的幅度转换为相位,再利用相位信息来计算频率值,因此对信噪比的要求较高,在实际应用中难以达到性能要求。全相位FFT抗噪性能好,且具有“初相不变性”,相位信息受FFT变换点数影响小,无需附加校正措施即可精确提取相位信息,与相位推算法相结合能得到测频精度高、抗噪性能强,瞬时性较好的全相位FFT-相位推算法测频方案。
1 全相位FFT-相位推算法基本原理
全相位FFT-相位推算法的基本原理是先分别对在时域上仅相差一个采样间隔的两序列分别进行apFFT变换,利用频谱信息测得两序列的中心样点的相位,然后根据其相位差,用相位推算法计算信号频率。算法流程如图1所示。

图1 apFFT-相位推算法流程图
1.1 相位推算法原理
复指数信号 x(t)=Amej(2πfmt+θ0)经过采样,采样频率为fs,得到复指数序列
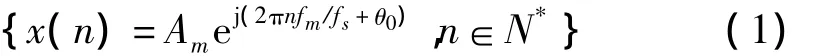
第n个采样点处的相位为θn=2πnfm/fs+θ0,在数字域瞬时频率和相位的关系为[3]
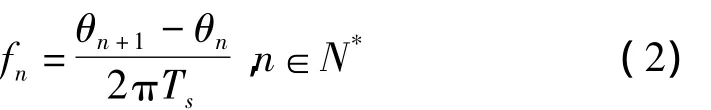
其中,θn为第n个样本点的相位值;Ts为采样间隔。频率推算的精度取决于相位测量的精度,在高信噪比条件下能得到较高的相位测量精度,若信噪比较低,则相位测量误差较大,导致频率测量错误。为提高相位测量的抗噪性,采用全相位FFT测相。
1.2 全相位FFT测相原理
假设输入采样序列为{…,x(-N+1),…,x(0),…,x(N-1),…},为分析序列的频谱特性,需要对序列作N点DFT变换。传统方法[4-5]是连续截取序列中的N个采样点,如x(0),x(1),…,x(N-1)作 FFT来实现,这种方法只考虑到了包含x(0)的一种截断情况,会产生严重的栅栏效应和频谱泄露,产生较大的测量误差。全相位FFT将包含x(0)的所有长度为N的分段序列都考虑在内,对序列进行全相位的预处理,产生一个长度为N的样值序列作FFT变换,具体步骤如下
(1)列出所有包含x(0)的长度为N的子数据向量
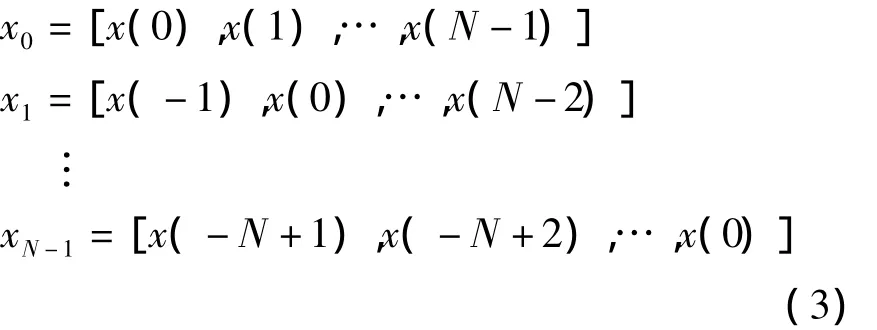
(2)对每个向量进行循环移位把样本点x(0)移到首位,得到另外的N个N维向量
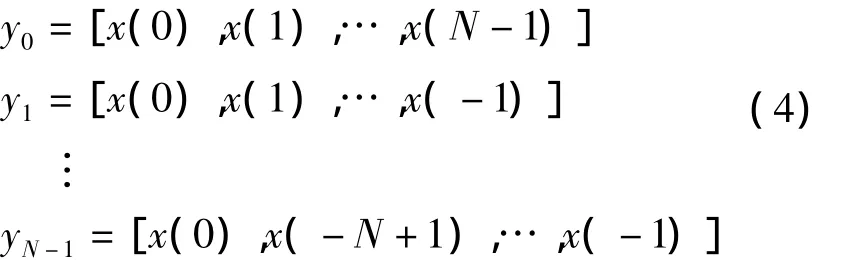
(3)对准x(0)相加取平均得到全相位数据向量
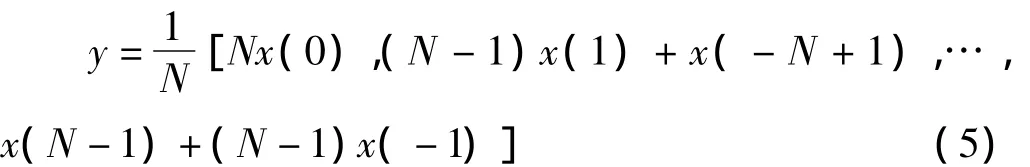
全相位数据向量的获得等价于用一卷积窗W(n)=f(n)*b(-n)对以x(0)为中心的,长度为(2N-1)的数据向量进行加权处理,再移位求和。此处为无窗时,f=b=RN,其中RN为长度为N的矩形窗,W为三角加权窗。双窗时,f=b=wN,其中wN为任何对称窗,如汉宁窗。以N=4为例,该过程如图2所示。
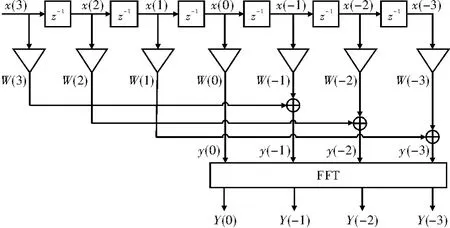
图2 apFFT谱分析基本框图(N=4)
根据DFT的移位性质,式(4)的yi的DFT变换Yi(k)和式(3)的xi的DFT变换Xi(k)之间有
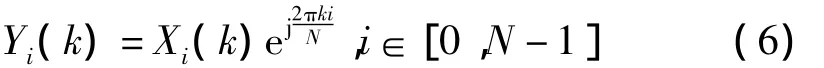
对于单频复指数序列{x(n)=Amej(2πmn/N+θ0)},式(5)的FFT输出即为
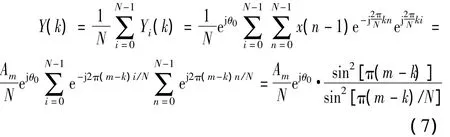
从式(7)可以看出,序列{x(n)=Amej(2πmn/N+θ0),-N+1≤n≤N-1}的全相位FFT谱旁谱线相对于主谱线的比值衰减快,主谱线突出,能够较好地抑制频谱泄露。全相位FFT谱的相位值θ0,即为中心样点x(0)的理论相位值,该值与频率偏离值m-k无关。即全相位FFT具有相位不变性,所测得相位精确度高,无需复杂的校正措施。为在FPGA中实现该方案并获得较高的测量精度,采用Cordic算法求取相位值。
1.3 Cordic算法
Cordic算法(The Coordinate Rotational Digital Computer)是一种用于计算常用基本运算函数和算术操作的循环迭代算法,基本思想是通过一系列固定的、与运算基数相关角度的不断偏摆以逼近所需要的旋转角度[6]。Cordic算法包含圆周坐标系、线性坐标系和双曲线坐标系3种旋转系统,本方案使用圆周坐标系下的旋转[7],其表达式如下
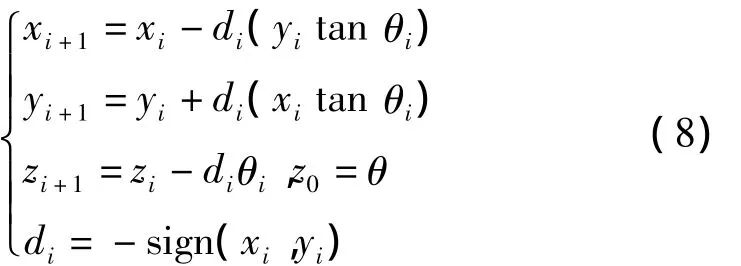
θi是每次旋转的角度,它是Cordic算法的核心,其中 tanθi=2-i,i∈[0,+ ∞)。此外表示在-99.7°≤θ≤99.7°范围内的任意角度都可以旋转,对于该范围外的角度,可以使用三角恒等式转化成该范围内的角度。di是一个判决算子,用于确定旋转的方向,其中经 n 次迭代后得到
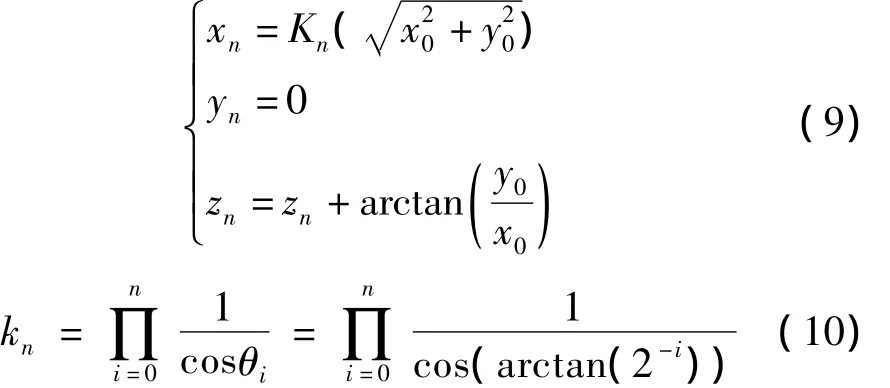
通过设定z0=0计算,将apFFT变换得到谱峰数据的虚部和实部分别作为x0和y0输入,通过n次迭代就能求得序列中心样点的相位θ0。Cordic算法在硬件上实现只需用到移位和加法运算,大幅节约了资源,能在工程上得到良好实现,满足设计要求。
2 FPGA实现
将图1的原理框图应用于实际工程中,其基于FPGA的测频系统的硬件系统节构框图如图3所示。
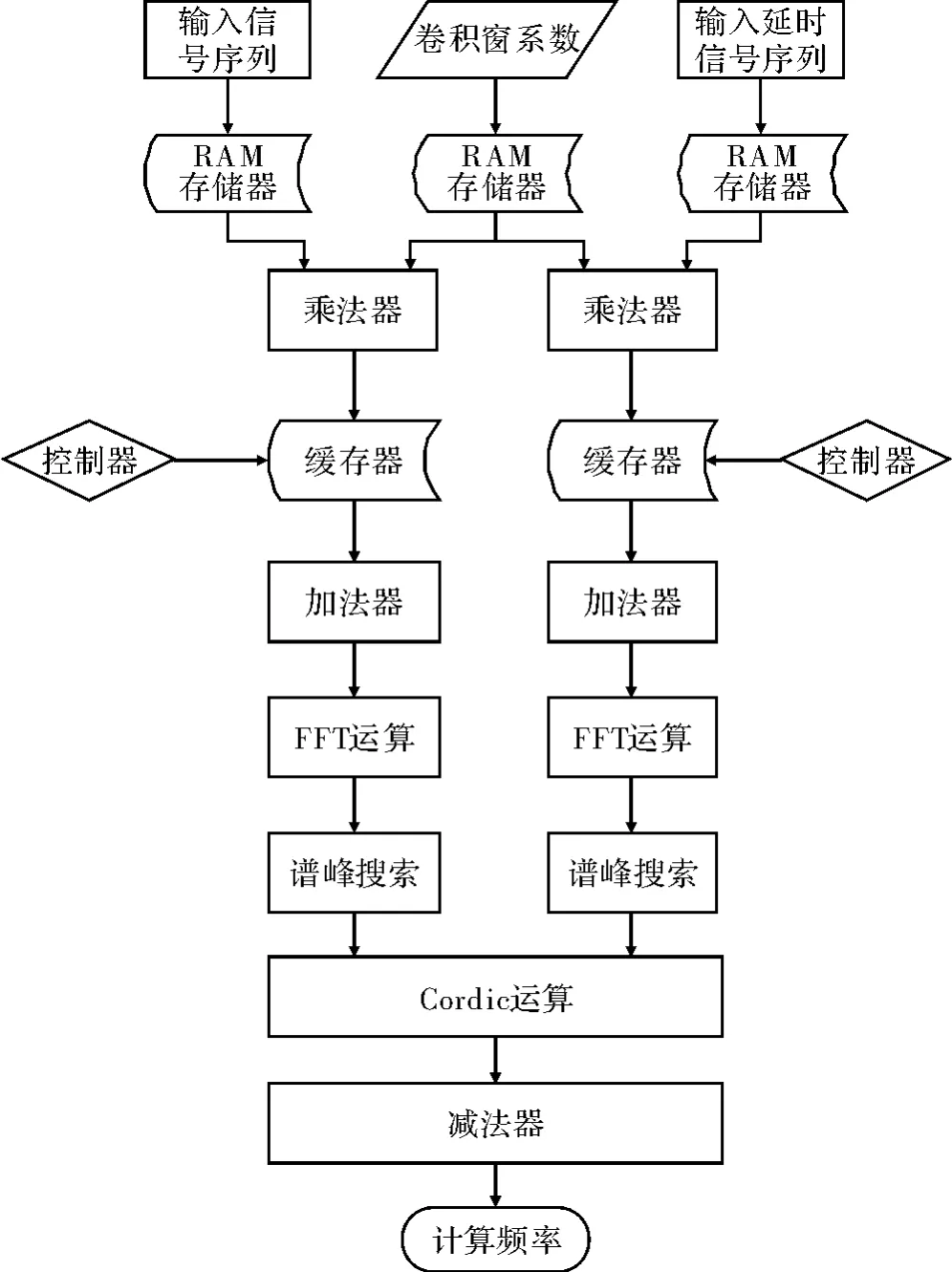
图3 基于FPGA的测频系统结构框图
整个系统由数据存储模块和数据运算模块和数据处理模块构成。数据存储模块由RAM模块、ROM模块和缓存器组成。RAM模块用于存储外部输入信号,完成采样时钟和处理时钟的转换;ROM模块用于存储卷积窗的系数;缓存模块用于数据缓存,与加法模块共同实现对数据的全相位预处理。数据运算模块包含乘法模块、加法模块、FFT运算模块和减法模块。乘法模块实现对输入数据的加窗处理;加法模块完成对数据的全相位预处理;FFT运算模块将预处理后的数据进行傅里叶变换;减法器模块用于计算两序列中心样点的相位差。数据处理模块由谱峰搜索模块和Cordic运算模块组成。谱峰搜索模块确定主谱线的位置以及对应的实部和虚部;Cordic运算模块求解主谱线对应的相位值,即序列中心样点的相位。
Cordic模块中用16 bit有符号数量化(-π,π]的角度范围,其中214表示π。假设载频为fm,采样率为fs,相位差符号整型值为Δφ,则频率计算公式为
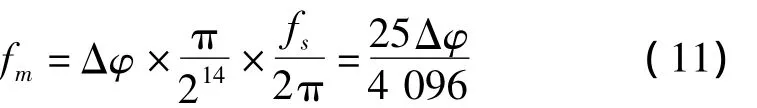
由于每次apFFT得到2N-1个采样点中心样点x(0)的相位,这样通过相位推算法计算出的频率即是采样点x(0)对应时刻的频率,前N-1个点和后N-1个点对应时刻的频率不能测得。若信号为单向调频信号,则会导致测量带宽偏小,且调斜率越大,带宽误差越大。为改善这种情况,采取计算信号的调斜率,并算出2(N-1)Ts时间对应的带宽,对测量带宽进行补偿
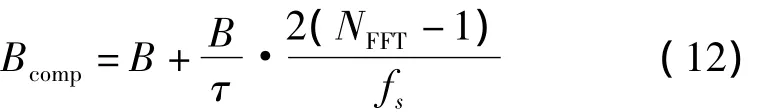
其中,Bcomp是补偿后的带宽;B是测量到的带宽;τ是脉宽;NFFT是FFT变换点数。
3 仿真验证
选用Altera公司StratixⅣ系列中的EP4SGX180KF40C3器件,使用Verilog语言完成电路描述后,在Quartus II和Modelsim软件平台上进行编译和仿真。用Matlab产生不同频率和带宽的单频信号和线性调频信号作为输入信号进行仿真,其中脉宽40μs,采样率为200 MHz,信噪比为10 dB,量化位数为12 bit,FFT点数N=64。载频为37.7 MHz的单频信号的仿真波形如图4和图5所示。

图4 单频信号的仿真结果

图5 单频信号的仿真结果
图中clk是工作时钟,pulse是脉冲包络,高电平期间有数据输入 phase_dif是两序列的相位差,PF是载频,PB是带宽。从图5可以看出,数据输入到结果输出只需约1.7μs,瞬时性较好。单频信号和线性调频信号的仿真结果分别如表1和表2所示。
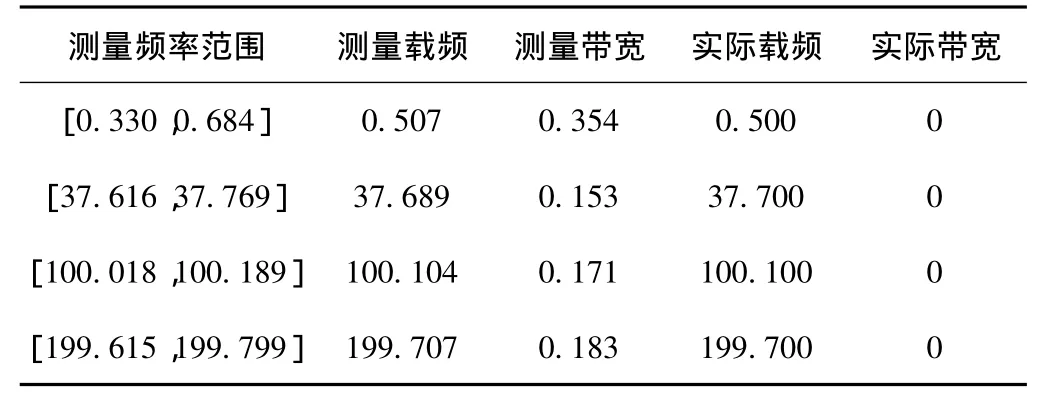
表1 单频信号测量仿真结果 MHz
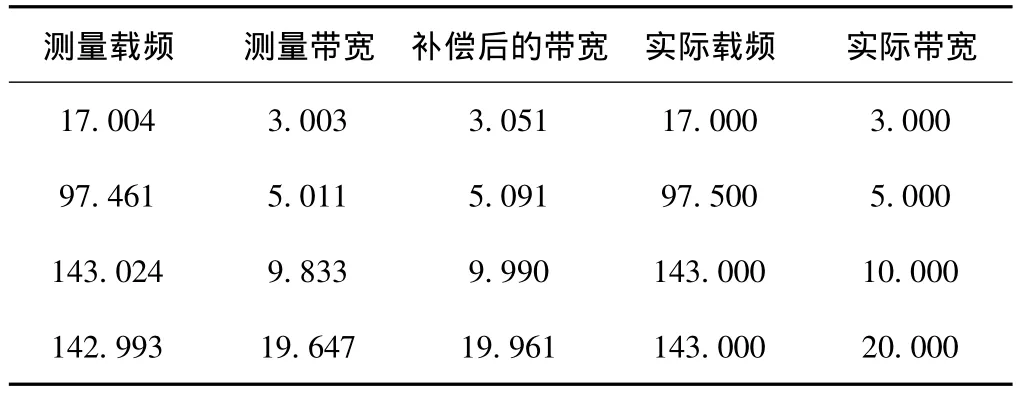
表2 线性调频信号测量仿真结果 MHz
从表1和表2的测量值与实际值的对比可以看出,该方法对载频的测量具有较高的精度。单频信号时带宽测量误差较大,主要原因是信号中的噪声引起了相位测量的误差。
4 结束语
将相位推算法与apFFT相结合应用于实际频率测量,在FPGA平台上进行了仿真。结果表明,该方法具有较好的瞬时性、测量精度高、且抗噪性能强,兼顾了相位推算法和apFFT的优点。此外,该方案理论简单,硬件资源占用少,易于在工程中实现,具有较高的实际工程应用价值。
[1]赵国庆.雷达对抗原理[M].西安:西安电子科技大学出版社,2005.
[2]周晓青,李合生,陶荣辉,等.数字测频算法研究综述[J].微型机与应用,2010(7):1-5.
[3]伍小保,王冰,何勤.Cordic算法数字瞬时测频的FPGA设计与实现[J].科技传播,2010(7):199-200.
[4]王兆华,黄翔东,杨尉.全相位FFT相位测量法[J].世界科技研究与发展,2007,29(4):28 -32.
[5]沈艳芳,陈丽花,陈星.基于FPGA的全相位FFT高精度相位测量[J].电子测量技术,2011,34(8):52 -55.
[6]杨宏,李国辉,刘立新.基于FPGA的Cordic算法的实现[J].西安邮电学院学报,2008,13(1):75 -77.
[7]耿丹.Cordic算法研究与实现[J].遥测遥控,2007,28(4):39-42.
[8]蔚接锁.基于FPGA与流水线Cordic算法的FFT处理器的实现[D].天津:天津大学,2008.
[9]王梦源,王书省,陈星.流水线双模Cordic算法的FPGA实现[J].电子测量技术,2007,30(9):184 -186.
[10]夏宇闻.Verilog数字系统设计教程[M].北京:北京航空航天大学出版社,2008.
