车载雷达信号接收机的数字下变频研究和实现

徐伟升

(西安电子科技大学电子工程学院，陕西西安 710071)

随着电子技术的不断发展，数字下变频技术逐渐替代模拟下变频，并且随着算法不断优化和更新。数字下变频是雷达信号接收机处理信号的重要部分，其能将高达几百MHz，最高频率甚至可达到几GHz的雷达信号转变为基带的低频信号，如此便使得各种数字信号处理模块可在基带信号下对信号进行处理［1］，解决了数字信号处理模块处理频率上的瓶颈问题。文中采用可编程器件 FPGA对该算法流程进行实现，能满足在高采样率下的信号时实处理要求［2］。

1 数字下变频的原理

数字下变频需要将输入的射频或高频信号经过A/D采样转换成数字信号进行处理，由于输入信号的中心频率较高，若依据奈奎斯特定理进行采样需较高的采样频率，难以实现［3］，且后续处理模块也难以满足较高的数据率。因此，本文采取带通采样定理:一个带限信号，其频率在(fL，fH)内变化，若采样频率fS满足

式中，m取值为0到满足fS≥2(fL－fH)的最大正整数，则用fS对上述信号进行等间隔采样，得到的采样值能准确地恢复出原信号。

设输入的模拟射频或高频信号可表示为

式中，f0为信号的中心频率，若经过带通采样，采样频率为fS，m为满足fS≥2(fL－fH)的最大正整数。则采样后的信号为

式中，xI(n)=a(n)cosφ(n)、xQ(n)=a(n)sinφ(n)为经过处理得到的基带信号。而如何处理得到想要的基带信号则是数字下变频的核心，数字混频［4］。

数字混频有很多种方法，其中最常用的是低通滤波法正交混频，让采样后的信号与两个正交本振序列cos(ω0n)和sin(ω0n)相乘，再通过低通滤波器滤掉高频部分得到基带信号，其中ω=2π。其原理示意

0图如图1所示。

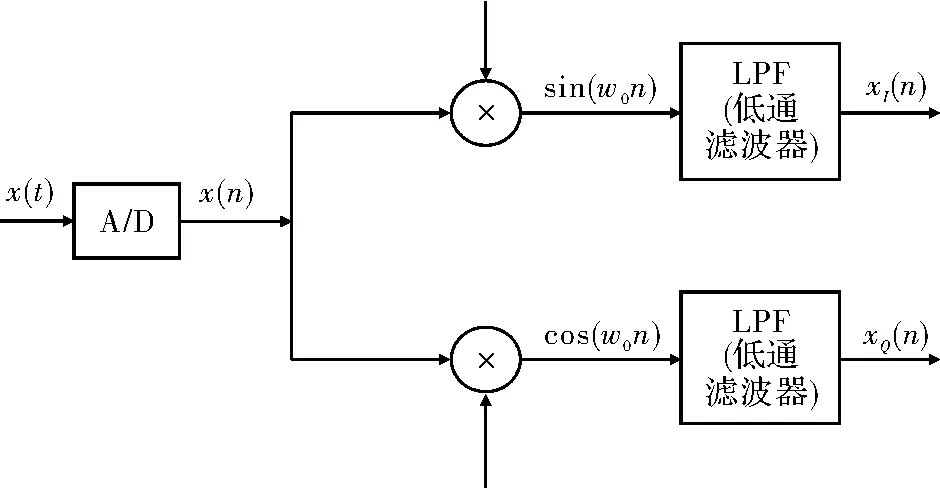
图1 低通滤波下变频原理图

其中x(n)乘以cos(ω0n)得

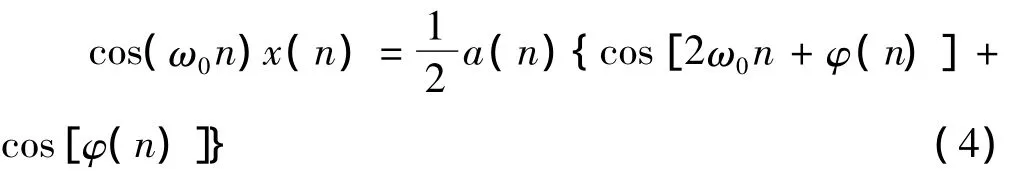
式中，cos［2ω0n+φ(n)］是混频后的高频分量，可通过低通滤波器将其滤除得到基带信号a(n)cos［φ(n)］。同理，x(n)乘以 sin［φ(n)］后，得

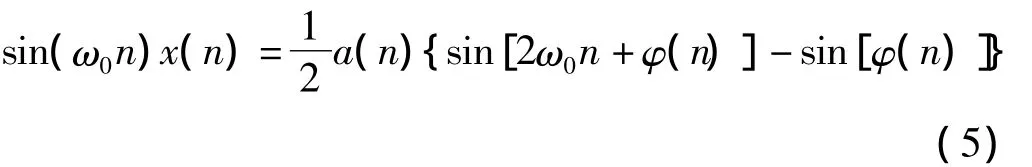
通过低通滤波器滤除混高频分量sin［2ω0n+φ(n)］，得到基带信号a(n)sin［φ(n)］。

这种基于低通滤波器的数字下变频主要基于模拟下变频的原理实现，对双路信号同时做变换，所用的滤波器系数相同［4］。这样两路信号通过低通滤波器时由于非理想滤波所引起的失真是一致的，对I、Q双路信号的幅度一致性和相位正交性并无影响，从而具有较好的负频谱对消功能，可达到较高的精度，且处理信号的带宽较宽［5］。

但处理后的数据率并未降低，当信号带宽远小于载波频率时，滤波器阶数较高，且需要加窗函数，在FPGA中实现复杂。在信号带宽远小于载波频率的情况下，为避免低通滤波在FPGA中的复杂算法，采用另外一种数字下变频算法，此时x(n)序列为

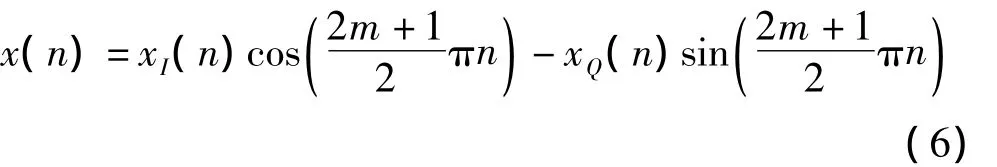
可得序列

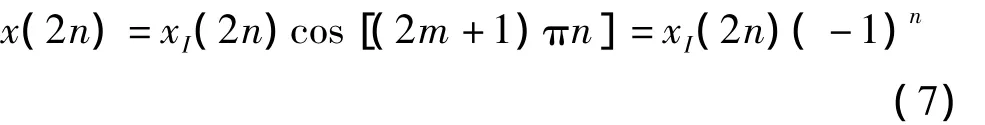
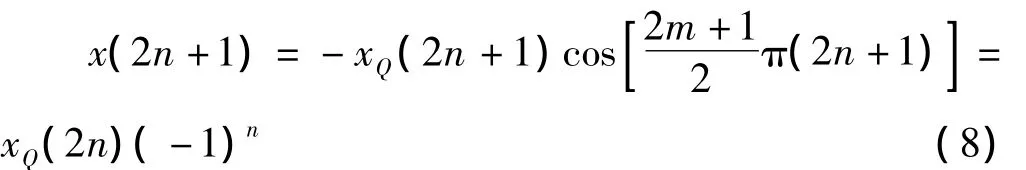
则序列

即x(2n)(－1)n和x(2n+1)(－1)n两个序列分别是同相分量xI(n)和正交分量xQ(n)的2倍抽取序列。而传统模拟方法中与两个正交的本振相乘就变成进行简单数学运算后的结果。因此，在具有较高精度的情况下，其正交性完全可以得到保证。上述采样结果是交替得到I路的偶数信号分量和Q路的奇数信号分量。由于采用奇偶抽取，I、Q两路信号分量在时域上相当于差半个采样点［5］。且由抽取原理可知，若xI(n)和xQ(n)的数字谱宽度 ＜π/2，则其两倍抽取序列xI(2n)和xQ(2n)可无失真表示原序列。则两个序列的频率响应为

由此可得到两种实现方法

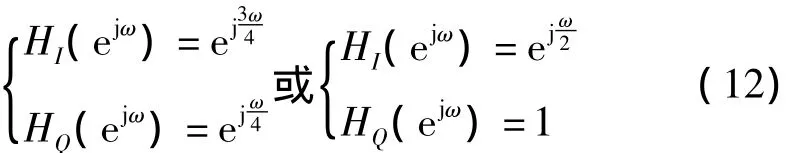
基于多相滤波的数字正交下变频实现过程，如图2所示。

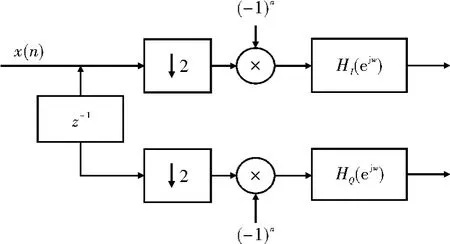
图2 多相滤波混频的数字下变频原理图

2 数字下变频的Matlab仿真和实现

利用Matlab对上述采用的基于多相滤波正交混频的数字下变频的算法进行仿真验证，为后续在FPGA的研究和实现提供了理论支持。由于对此种下变频算法的研究是为了对车载巡航雷达信号进行处理，因此设模拟信号中心频率f0为31.2 MHz，带宽B为50 kHz的线性调频信号。则依据带通采样定理，m取值为0到满足fS≥2(fL－fH)的整数。其中，m越大，采样率越小，数据率也就越小，其对后续数据的处理越简单。因此，假设采样率fS为9.6 MHz，仿真时序波形和频域谱线如图3(a)所示［6］。其中，模拟信号经采样，其频域谱线发生频移，中心频率移至fS/4处，如图3(b)所示。谱线移至±2.4 MHz处［7］。再经奇偶抽取和正负变换产生正交两路信号，此时频谱移至零频处，时域波形与频谱如图4所示。

图3 时序波形和频域谱线

图4 IQ两路信号分量时域波形和频域谱线

正交两路信号再经过延时滤波和消除时间差后，得到了完整的正交基带信号。而延时滤波器的设计是算法的核心。根据基于多相滤波的数字正交下变频中的滤波器频率响应要求，选择

作为滤波器的频率响应。可从此频率响应看出I，Q两路滤波器是全通滤波器，而相位响应分别是θ(ω)=和θ(ω)=。利用频率采样法来实现此滤波器，文中用N=8点对HI(ejω)进行采样，采样规则是对ω在ω=0～2π之间等间隔采样N点。对采样后的HI(ejω)进行IDFT即可得到所需的h(n)。

图5和图6是设计完成后的滤波器幅度特性和相位特性，图 5(a)是 HQ(ejω)=的幅相频域响应曲线图，幅度在频域上接近全通，相位响应满足线性要求，所以滤波器符合设计要求。图5(b)是HQ(ejω)=ejω4的幅度时域响应曲线图，因设计的滤波器在频域是全通的，所以其幅度在时域方面为冲激函数的形式。而的幅度响应也是一个冲激函数，只在时域和 HQ(ejω)=的冲激函数上有一个偏差［6］。

图5 Q路滤波器幅相特性

图6 I路滤波器幅相特性

以下是经过延时滤波处理后的正交IQ两路信号，时域波形如图7所示，图6(b)是正交特性效果，正交圆表明IQ基带信号具有较好的正交特性。由此说明，基于多相滤波的混频数字下变频算法在Matlab中成功实现。

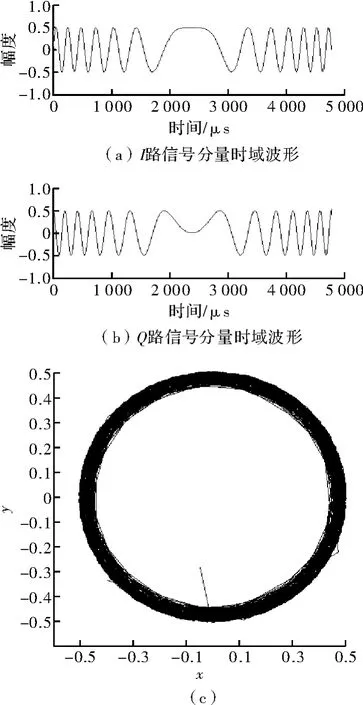
图7 延时滤波后IQ基带信号时域波形和正交效果

3 数字下变频在FPGA中的研究和实现

根据多相滤波正交混频的数字下变频算法在Matlab中仿真实现，整个数字下变频算法在FPGA中实现需3个过程:奇偶抽取、正负变换和延时滤波［9］。

3.1 奇偶抽取和正负变换模块

为实现奇偶抽取，先对采样后的信号进行奇数倍抽取，降低采样率和数据率，减轻数字下变频模块的压力。然后将信号延时一个采样周期，再对延时后的信号和无延时信号同时进行二倍抽取，得到IQ两路信号。奇偶抽取后，对IQ两路信号进行正负变换，消除IQ两路信号分量的正负因子。

3.2 滤波器的结构分析

经正负变换后，进入延时滤波，即在FPGA中实现延时滤波器，文中采用FIR结构来实现。L阶或长度为L的FIR输出对应于输入时间序列x［n］的关系由一种有限卷积数量形式给出，具体形式如下

其中，从f［0］≠0一直到 f［L－1］≠0均是滤波器的 L阶系数，同时也对应于FIR的脉冲响应。

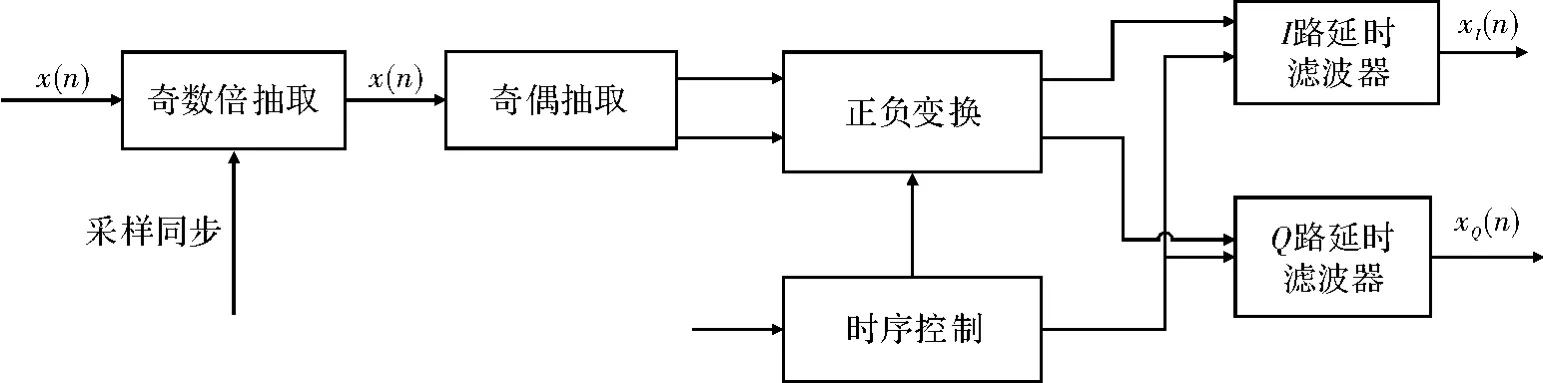
图8 数字下变频在FPGA中的结构

图9 直接式FIR滤波器结构

可将这一直接形式的FIR滤波器进行改变，转变为图10的形式。这种新形式的FIR滤波器称为转置式FIR滤波器。

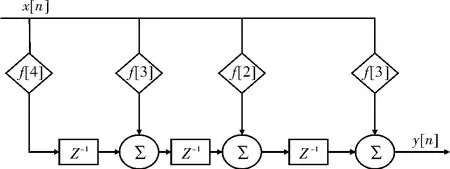
图10 转置式FIR滤波器结构

这种新形式的FIR滤波器优点在于无需x［n］提供额外的移位寄存器，且不必为达到高通过量而给乘积的加法器添加额外的流水线级。

3.3 延时滤波器在FPGA中实现

因此，在FPGA程序中设计转置式的延时FIR滤波器。首先，在Matlab中产生延时滤波器的系数，根据上述对延时滤波器的研究，文中设计41阶的纹波滤波器，让Matlab产生所需的延时滤波器系数，再将其转换成可寄存在FPGA程序中的数据格式。FPGA采用Altera公司的Cyclone II系列，可将转化后的延时滤波系数存储在FPGA的ROM IP核内，这样既节省了程序开发时间，又能简化程序。引用ROM IP核的程序，可通过地址信号读取存储在ROM中的滤波系数［4］。然后再让信号和延时滤波系数相乘，再依次累加，得到延时滤波后的IQ正交信号分量。同时，可抽取降低采样率和数据率，到此整个基于多相滤波混频的数字下变频在FPGA中得以实现，随后，需验证其正确性。

3.4 数字下变频在FPGA中的仿真和实现

在FPGA实际运行中，车载雷达信号的载频是31.2 MHz，带宽＜50 kHz，由于A/D芯片的采样频率最低为5 MHz。为满足带通采样定理，文中采用9.6 MHz的频率对信号进行带通采样。由于采样后的数据率较高，故需要对信号进行奇数倍抽取，抽取后再进行数字下变频。图11是抽取后的数字下变频仿真结果［4］。

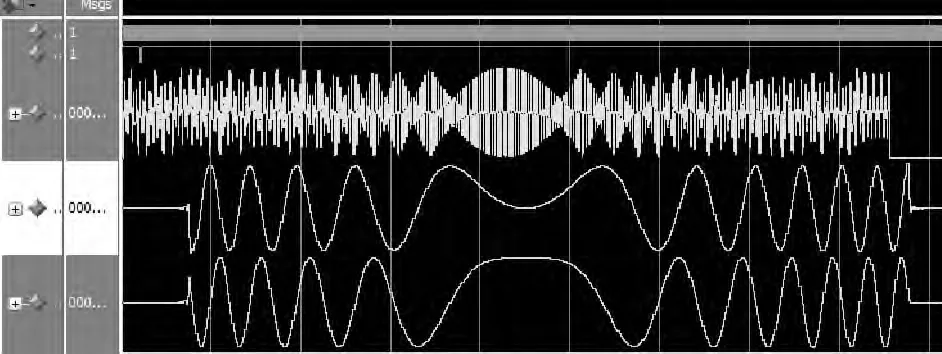
图11 数字下变频在FPGA中的仿真波形

其中，第1条波形是下变频前的信号序列，第2条和第3条波形分别为下变频后正交两路基带信号分量，其与Matlab的理论仿真结果一致。故表明了基于多相滤波混频的高性能数字下变频算法在FPGA中仿真成功。

通过车载雷达的前段天线获取雷达信号，然后从接收机接收处理后的数据，再经分析处理后的雷达基带信号满足接收机的设计指标。从而表明，在车载雷达信号接收机中应用的基于多相滤波混频的数字下变频算法成功实现［9］。

4 结束语

基于下变频的基本原理，通过Matlab对数字下变频进行了理论研究与分析，提出了一种高性能基于多相滤波混频的数字下变频算法，并在FPGA中进行了研究和实现。本文的数字下变频算法的研究就是基于车载雷达信号接收机的研发，车载雷达信号的中心频率远大于信号带宽，为了能无失真地得到有效基带信号，必须对雷达信号进行下变频处理。因此，一般的低通滤波混频的数字下变频算法和较复杂的下变频算法均不适用于车载雷达信号接收机的信号处理。为此，提出了基于多相滤波混频的数字下变频算法，该算法不仅能实现无失真的信号处理，还可简化雷达信号接收机的信号处理系统。

［1］徐文明，刘渝.FPGA在数字信道化接收机中的应用［J］.雷达与对抗，2005(1):50－54.

［2］吕幼新，郑立岗，王丽华.基于多相滤波的宽带数字化接收机技术［J］.电子科技大学学报，2003，32(2):133－136.

［3］Ray Andraka Andraka Consulting Group，Inc.A survey of cordic algorithms for FPGA based computers［C］.ACM New York，NY:Proceeding FPGA'98 Proceedings of the 1998 ACM/SIGDA Sixth International Symposium on Field Programmable Gate Arrays，1998:191 － 200.

［4］崔航，冯小平.基于FPGA的软件无线电数字信道化接收机设计［J］.电子元器件应用，2008(10):42－43.

［5］戴绍港，张福洪.软件无线电信道化接收机的FPGA实现方案［J］.杭州电子工业学院学报，2004，24(4):47 －51.

［6］孙建伟.超小型雷达侦察接收机及关键技术研究［D］.西安:西安电子科技大学，2009.

［7］丁海锋;张志强;赵前晟.基于FPGA的数据采集板设计与实现［J］.电子科技，2010，23(3):30 －33.

［8］庞少龙，马志刚，吴子贤.一种新型高速宽带数字下变频器的 FPGA 实现［J］.电子科技，2013，26(9):106－109，112.

［9］常虹，赵国庆，牛新亮.高效的宽带数字信道化接收机设计［J］.西安电子科技大学学报，2010，37(3):464－468.