用有限差分法分析电介质静电场特性

唐正明，章三妹，冯正勇

(1.西华师范大学物理与电子信息学院，四川 南充 637009；2.西华师范大学实验中心，四川 南充 637009)

用有限差分法分析电介质静电场特性

唐正明1，章三妹2，冯正勇1

(1.西华师范大学物理与电子信息学院，四川 南充 637009；2.西华师范大学实验中心，四川 南充 637009)

电介质内的电位分布、电场分布和极化等特性相对常规静电场问题难于理解.在介绍有限差分法求电位分布原理的基础上，导出了介质中拉普拉斯方程的有限差分形式；通过巧妙设计非均匀介质区域并运用Matlab求解，分析了电介质的静电场特性.理论分析与仿真计算结果符合较好.

有限差分法；介质极化；静电场；Matlab

常用的计算电磁场问题的方法主要有两大类:第一类是解析法；第二类是数值法.伴随工程问题复杂度的提升及计算机处理能力的显著提高，数值法应用日趋广泛.二维静态电磁场的边值问题是求解电磁场的基础，有较为经典的解析法[1].然而，就其数值法求解来说，一方面，现有文献所介绍的多为典型的“电解槽”类问题，且常局限于单一媒质[2-4]，这对理解电介质的静电场特性，尤其是电介质的极化特性[5]极为不利；另一方面，实际媒质的本构关系具有多样性[6]，局限于单一媒质的基础研究，已不能满足实际应用的需要.由于有限差分法(Finite Difference Method)求解静电场边值问题较为有效，同时，其也是广泛应用于时谐场分析的时域有限差分法(Time Domain Finite Difference Method)的基础[7-10].为实现对电介质极化问题和有限差分法更为准确而全面的掌握，本文在传统有限差分法求电位分布问题的基础上，将有限差分法运用到介质极化问题分析中，导出了介质中拉普拉斯方程的有限差分法形式，并借此分析了电介质的静电场特性.

1 电介质的极化特性

无论是极性还是无极性分子中的束缚电荷，在外电场的作用下均会产生一定的位移，并形成顺着外电场方向规则排布的电偶极子.大量电偶极子的存在，将在电介质内形成附加电场，而最终使得电介质区域的总电场

其中，χe为电介质的电极化率.将真空中的高斯定律推广应用于电介质中，可得

式中，ρf、ρP分别为自由电荷密度和因电介质极化而产生的极化电荷体密度

同时，由(5)知电介质的本构关系，满足

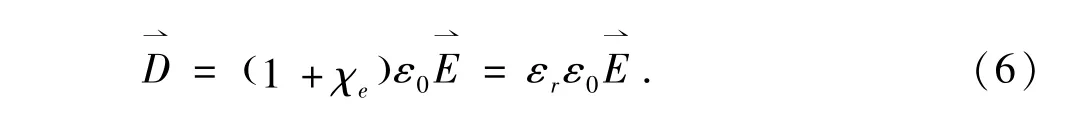
其中，εr称为介质相对介电常数，用于表征电介质的极化特性，比电介质的电极化率χe更为常用.在同一外电场照射下的两种不同电介质，设其相对介电常数分别为εr1和εr2，由静电场的法向边界条件，有

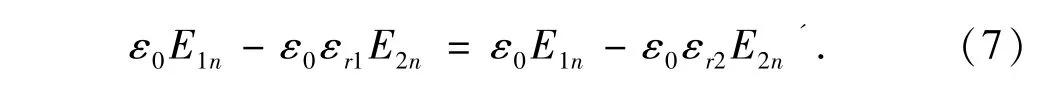
其中，E1n，E2n和E2n'分别为入射电场、介质1内部和介质2内部电场的法向分量.由此可见，在所加外电场不变的情况下，相对介电常数ε较大的介质内的总电场E较小.这与前面提及的电介质附加电场的“克服作用”相符合.

2 介质区域的有限差分法形式

有限差分法的原理在于，在变量增量充分小的前提下，函数可进行泰勒展开，并忽略掉高阶项，进而利用差分近似的替代微分运算[11-13].例如，可通过泰勒公式得到关于函数f(x)微分的中心差分形式

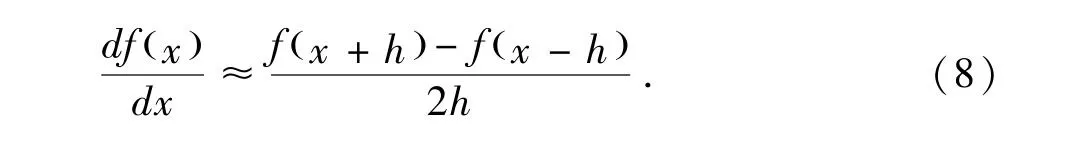
由于Maxwell方程由偏微分方程所描述，而偏微分方程也可以做类似的差分表示.因此，有限差分法可用于静电场问题分析中.在数值实现上，首先将求解区域划分成网格，然后将区域内连续的场分布，按照有限差分法理论，用网格节点上的离散的数值解代替.为了描述方便，将区域采用边长为h的正方形网格离散(h即为离散步长)，并将相应节点放大显示，其中，坐标为(i，j)的节点电位的电位为φi，j，其周围4个节点的电位分别为φi+1，j、φi，j+1、φi-1，j、φi，j-1，如图所示1.

图1 节点顺序图Fig.1 Diagram of node sequence

显然，离散步长h将直接影响到数值解的精度，这从泰勒展开也可看出.泰勒级数的近似条件要求增量充分小(即要求离散步长h充分小，此为相对概念，工程上一般标准为，如计算域沿着某个方向的长度为l，则可令).此情况下，各个节点的电位可表示成以φi，j为基点的泰勒级数形式，在保证精度的前提下略去高阶项，进而可得到周围4点电位与中心点电位的关系.

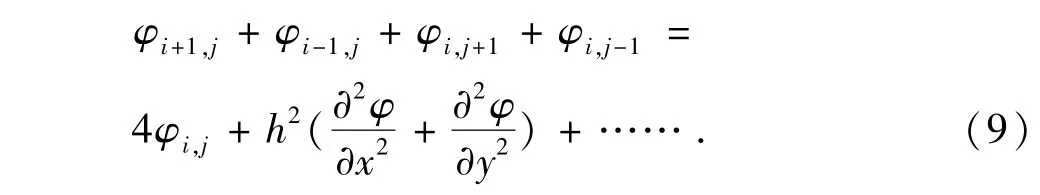
由于静电场中的任何点均满足泊松方程

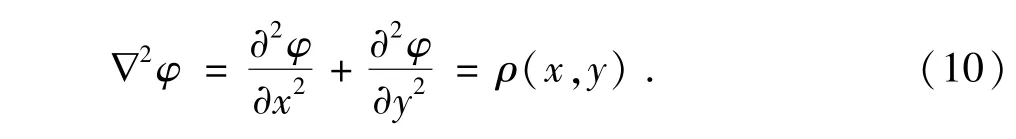
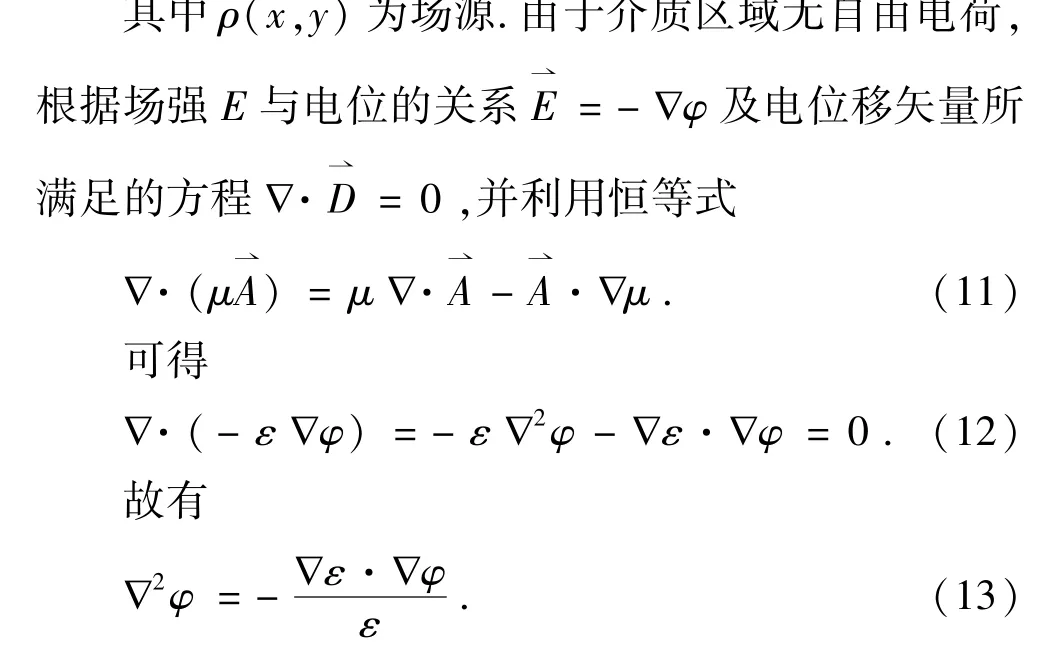
联立(10)—(13)，得介质区域拉普拉斯方程的有限差分形式

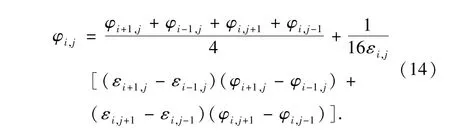
3 电介质区域的静电特性分析

为验证电介质的静电场特性，设计了如下图所示的非均匀介质区域:无限长矩形腔，横截面为3m∗2m，其中央有一截面方向1m长，直流电压为1V的无限长平板，由相对介电常数为19的介质区域所支撑，腔的其余部分为空气填充，相对介电常数为1，四周为理想接地导体.

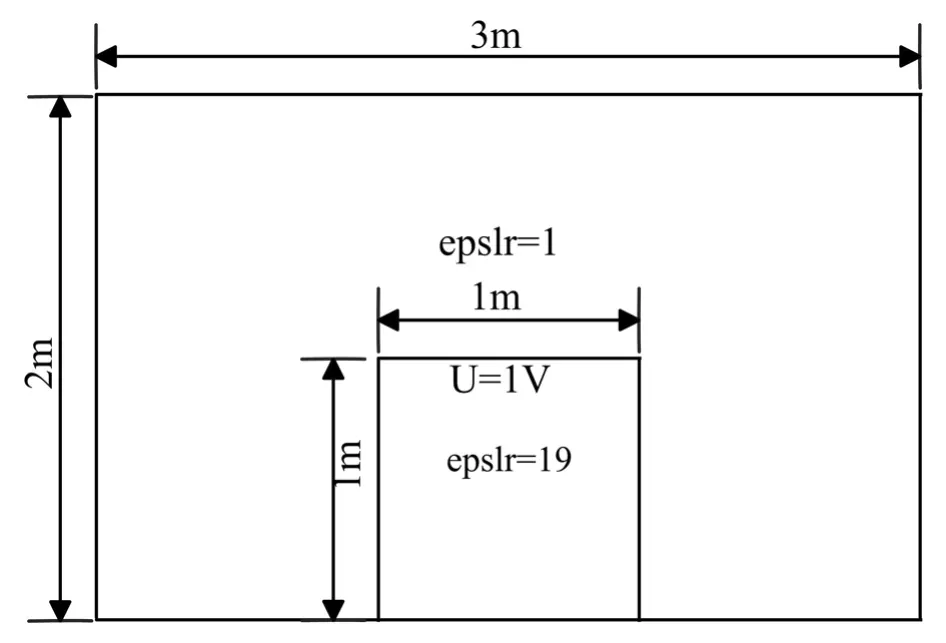
图2 求解区域示意图Fig.2 Schematic diagram of solving region

将计算区域划分为30∗20个单元格，非均匀介质中电位的有限差分形式用赛德尔迭代法表示并采用Matlab编程[14-15].为了显示上的直观，程序选择输出了电位分布三维曲面图和等位线、电场线分布图.

图3 电位、电场分布图Fig.3 Potential，electric field distribution

从结果来看，等位线在介电常数较高的区域相对密集，即电位梯度较小，因而该区域内场强相对较小.就其根源，是因为在介电常数较高的区域，电介质的极化产生的附加电场更大，从而使得该区域内的总场相对于介电常数较低的区域，有所减小.上述结果与前述相关基础理论相吻合.

4 结论

在对电介质的极化特性和有限差分法做简要介绍的基础上，详细分析了介质极化强度与区域内电场强度间的关系，并运用有限差分方法计算对比了不同介电常数区域内的电位、电场分布.所做分析使得相对抽象的电介质极化特性等理论具体化且易于理解.可将类似的方法拓展到讨论含自由电荷的介质区域，进一步用数值方法直观分析电介质极化电荷体密度、面密度，边界条件等相关特性.

[1]王礼祥.静态场边值问题的分离变量法理论研究[J]西南民族大学学报:自然科学版，2011，37(3):360-367.

[2]王洁，陈超波.基于MATLAB的静态场边值问题有限差分法的研究[J]微计算机应用，2010，31(3):1-5.

[3]赵德奎，刘勇.MATLAB在有限差分法数值计算中的应用[J].四川理工学院学报:自然科学版，2005，18(4):61-64.

[4]宋燎原，王平，张海峰等.静态电磁场边值问题计算方法[J].大学物理，2007，26(8):23-26.

[5]P劳兰，D R考森.电磁场与电磁波[M].陈成钧，译.北京:人民教育出版社，1979:62-87.

[6]肖峻，肖培.电磁媒质的本构关系[J].西南民族大学学报:自然科学版，2011，37(5):72-74.

[7]HYUN S Y，KIM S Y.3-D Thin-wire FDTD analysis of coaxial probe fed in asymmetric microwave components[J].Microwave Theory and Techniques，IEEE Transactions on，2011，59(11):2808-2815.

[8]OHTANI T，KANAI Y，COLE J B.A stability improvement technique using PML condition for the three-dimensional nonuniform mesh nonstandard FDTD method[J].Magnetics，IEEE Transactions on，2013，49 (5):1569-1572.

[9]王为，覃宇建，刘培国，等.基于高阶时域有限差分法与改进节点分析法混合求解复杂传输线网络瞬态响应[J].电子与信息学报，2012，34(12):2999-3005.

[10]朱小敏，任新成，郭立新.指数型粗糙地面与上方矩形截面柱宽带电磁散射的时域有限差分法研究[J].物理学报，2014，63(5):1 -7.

[11]BOOTON R C.Computational methods for electromagnetics and microwaves[M].New York:Wiley，1992:19-39.

[12]孙小东，李振春，王小六.三角网格有限差分法叠前逆时偏移方法研究[J].地球物理学进展，2012，27(5):2077-2083.

[13]冯慈璋.电磁场[M].2版.北京:高等教育出版社，1979:226-244.

[14]郑阿奇，曹弋.科学计算中的偏微分方程有限差分法[M].北京:电子工业出版社，2006:127-140.

[15]何红雨.电磁场数值计算法与MATLAB实现[M].武汉:华中科技大学出版社，2004:93-127.

(责任编辑:付强，张阳，李建忠，罗敏；英文编辑:周序林)

Application of finite difference method in analyzing the electrostatic properties of dielectric

TANG Zheng-ming1，ZHANG San-mei2，FENG Zheng-yong1
(1.School of Physics and Electronic Information，China West Normal University，Nanchong 637009，P.R.C.；
2.Experiment Center，China West Normal University，Nanchong 637009，P.R.C.)

It is more difficult to understand potential distribution，electric field distribution and the polarization characteristics in dielectric than conventional electrostatic field problems.This paper introduces the principle of finite difference method used in analyzing the potential distribution，and presents the calculation formula for dielectric region.Through the ingenious design and using Matlab to solve the inhomogeneous medium area，the static electric field properties of dielectric are analyzed.Theoretical analysis coincides with simulation results very well

finite difference method；dielectric polarization；electrostatic field；Matlab

O412.3

A

2095-4271(2015)04-0494-04

10.11920/xnmdzk.2015.04.019

2014-12-29

唐正明(1981-)，男，四川安岳人，讲师，博士研究生，主要从事微波、电子技术等方面的教学和科研工作.E-mail: zhengmtang＠163.com.

四川省教育厅项目(13BZ0010)