＊注浆抬升位移预测及简化模型研究

章 敏，刘军军，秦文权（．太原理工大学建筑与土木工程学院，太原03004；．广东省电力设计研究院，广州50663）



＊注浆抬升位移预测及简化模型研究

章 敏1，刘军军1，秦文权2
（1．太原理工大学建筑与土木工程学院，太原030024；2．广东省电力设计研究院，广州510663）

摘 要：将地层注浆引起的地表隆起视为随机过程，并假定抬升效果为地层中一连串浆泡径向扩张引起的变形效应之和，根据随机介质理论及线性叠加原理，推导出了多浆泡在均匀及非均匀两种扩张模式下地表抬升变形的理论计算公式及其简化形式。通过对比不同计算方法，发现对于浆泡均匀扩张模式，简化解可有效预测地表抬升位移，而对于非均匀扩张模式，精确法结果则更为合理。分析结果表明：随着浆泡间距的增大，地表抬升位移逐渐从“单峰”形式过渡到“双峰”形式；抬升引起的地表水平位移和倾斜在曲线分布形态和峰值点位置方面基本相同；同时在注浆施工中应加强地表曲率的监测，避免曲率过大反而造成建筑物的破坏。

关键词：注浆；地表抬升；随机介质理论；简化模型

科研基金（20120162110023）

在城市地铁、深基坑等市政工程施工中，穿越或紧邻既有建筑物的现象已日益普遍，如何控制和恢复地层损失所带来的建筑物倾斜、沉降等不良变形是项目成功的关键。注浆顶升技术作为一种有效的建筑物沉降恢复和纠偏手段，在工程结构的安全性控制中得到了广泛应用。Wisser等［1］通过对无厚度界面单元施加内部压力来模拟压密注浆，分析了隧道开挖及注浆加固对地表建筑物变形的影响。唐智伟等［2］针对崇文门地铁车站下穿既有线的抬升工程，提出了施加虚拟压力来模拟“注浆单元”扩张的数值方法。随后，孙峰［3］进一步将其应用于热力管道的注浆抬升研究中。为避免注浆抬升对既有结构造成不利的应力集中，张晓丽等［4］提出在基础弱化位置注浆的理念，并对该位置的确定进行了分析。易晓明［5］和侯艳娟［6］就注浆抬升作用机制、抬升量预测和施工技术要点进行了全面阐述。此外，笔者基于随机介质理论，将注浆抬升视为岩土开挖引起的地表沉陷的逆过程，推导出了单浆泡径向扩张条件下地表抬升变形的解析公式，并与施加体积应变得到的数值结果进行了对比［7］。

现场注浆抬升中，往往形成的注浆帷幕范围广，厚度大，因此需进行多孔注浆才能满足要求。在浆液扩散范围内，土体孔隙被填充，邻近管周土体被径向挤密而形成分界面，并伴随弹塑性变形。由于多孔、多段注浆形成的一连串浆泡彼此相互影响，将土体视为弹塑性体，运用经典力学逐个求解浆泡扩张引起的地层移动并进行叠加，将使问题变得十分复杂。而采用施加虚拟内力模拟浆泡扩张的有限元方法，需反复试算寻求最优膨胀压力，使其体积应变达到目标增量，这对于浆泡单元较多的复杂模型，试算过程势必耗费大量的计算资源。

鉴于以上背景，笔者引入随机介质理论，从概率统计的角度，将注浆引起的地表抬升视为一随机事件，将作者提出的单浆泡扩张引起的抬升位移预测方法进一步推广到多浆泡扩张的实际情况，求得了地表抬升变形的理论表达式及其简化形式，并通过数值方法验证了模型的合理性，以期为注浆抬升工程提供一套计算简便且实用的位移预测模型。

1　多浆泡扩张引起地表抬升的理论解

1．1 计算模型

当采用袖阀管分段注浆抬升时，在劈裂灌浆的鼓泡压密阶段，浆液将在出浆口附近土体中形成一连串近似球形的浆泡，其变形可视为球形扩张问题。地表抬升的最终位移，可认为是连续注浆过程中各浆泡扩张引起的变形效应的叠加。图1为浆泡分布及地表抬升示意图。浆泡半径为R，径向扩张量为ΔR，地层影响角为β，球心深度为Hi。图2为浆泡等量（均匀）和非等量（非均匀）两种径向扩张位移模式。对于均质土层，当浆泡发生径向扩张后，隆起地表将形成以通过浆泡球心竖轴为对称轴的旋转曲面。由于问题涉及三维空间效应，根据变形特点，以下模型求解均在球坐标系下进行。

图1　多浆泡扩张与地表抬升示意图

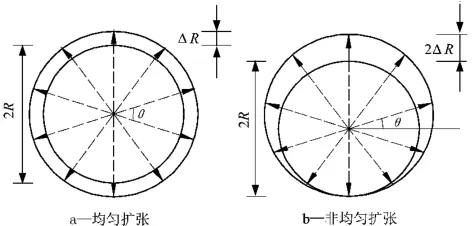
图2　浆泡扩张变形模式

1．2 地表抬升变形的求解

视岩土体为随机介质，由注浆引起的地层移动便可借助随机方法加以研究。对于坐标为x，y的地表任意观测点A，在文献［7］推导的单浆泡扩张抬升变形公式的基础上，根据叠加原理，易知其地表抬升量W和水平位移U可分别表示为：式中，角度γi为观测点到球心投影点的矢径与x轴的夹角，可根据A点和Oi′点的坐标（x，y）、（xi，yi）确定，且0≤γi≤2π。径向扩张量ΔR可根据注浆压力和土层参数，近似按球形小孔扩张理论求得［8］。

对于A点两个水平方向的地表倾斜Tx、Ty和地表曲率Kx、Ky，其表达式与水平位移表述式（2）类似，仅需将式中ui分别用ti、ki代替即可。式中被积函数wi、ui、ti、ki分别代表第i个浆泡深度z处微元体引起的地表变形，表达式分别为：

η

i式中：ηi＝Hi－ρcosφ；ε＝ρsinφ；Ai为地表观测点到第i个浆泡中心轴的距离；β为地层影响角，可按经验公式tanβ＝1

（k 2槡

π）近似取值，其中，k称为沉降槽宽度参数，一般土质越软，取值越大。对于砂土，k可取0．2～0．3；对于硬质黏土，大约取0．4～0．5；而对于较软的粉质黏土可达到0．7［10］。

当浆泡采用非均匀扩张模式时，根据文献［7］，可得地表抬升位移为：

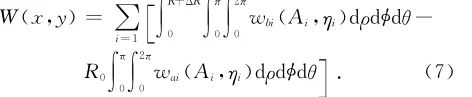
n式中，wai，wbi分别代表第i个浆泡膨胀前和膨胀后的地表抬升量，可分别用ηai和ηbi代替式（3）中的ηi得到，ηbi＝Hi－ΔR－ρcosφ，ηai＝Hi－ρcosφ，φ为浆泡球面点与水平面的夹角。相应地，地表水平位移、倾斜和曲率公式均可参照式（7）依次列出，限于篇幅，此处不再赘述。上述积分公式一旦求出，抬升后的整个地表曲面形态就可完全确定。

1．3 简化随机介质法

为避免对上述三重积分进行复杂的数值计算，由文献［11］的研究结果可知，当注浆点埋深与注浆扩散半径的比值较大时，整个注浆区域所增加的体积相对于周围岩土体来说可以认为是一微元，则浆泡体积膨胀引起的地表抬升量可简化为如下形式：

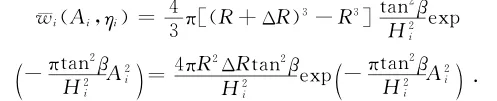
采用以上简化思路，并结合叠加原理，多浆泡球形扩张下地表抬升、水平位移、倾斜及曲率的简化公式可表示为：

n

对于非均匀扩张，在假定浆泡扩张模式为图2 （b）形式时，忽略二阶及以上小量，则注浆前后的浆泡体积增量近似为：

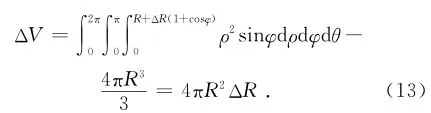
以上体积变化量与均匀扩张模式下的体积变化相等，故对于两种位移扩张模式，采用简化随机介质理论将得到相同的地表变形公式。这表明，对于简化解，地表抬升变形与所选择的位移扩张模式无关，仅取决于浆泡的体积应变增量和浆泡埋深。

2　计算与讨论

为验证随机介质法预测注浆抬升位移的可行性，本文结合数值模拟方法，采用文献［7］提出的体积应变法模拟浆泡膨胀，对双浆泡均匀扩张和非均匀扩张进行了对比分析。模型土体假定为弹性材料，弹性模量为10MPa，泊松比为0．4。两浆泡均位于5m深度处，浆泡半径均为1．5m，体积膨胀率为10%，中心距为5m。考虑到土体模量较低，土质较软，沉降槽宽度参数按较大值考虑，k取为0．7。两种位移扩张模式下的土层位移分布云图如图3所示。

图4　荷载－盒维数曲线对比Fig．4 Load－box dimension curve contrast

图4为均匀和非均匀两种位移扩张模式下地表抬升位移的分布曲线，其中将两浆泡对称轴与地表的交点设为坐标原点。由图可知，抬升曲线呈现出典型的“单峰”分布形态，最大位移发生在原点处，并随着向两侧距离的延伸逐渐减小。图5给出了三种计算方法得到的地表倾斜和曲率分布曲线。可见，原点处的地表倾斜值为0，但随距离的增大，倾斜值逐渐增大，在5m附近处达到最大值，随后，则逐渐降低直至趋向于0。值得说明的是，对于地表倾斜和地表水平位移（见图6），两者曲线的分布模式基本一致，峰值所在位置通常也基本相同。从图4和图5还可看出，采用随机介质法（以下简称精确法）、简化法和数值法三类计算方法得到的地表变形规律基本一致，仅曲线峰值存在一定差异。总的说来，对于均匀扩张模式，简化法与精确法得到的地表抬升变形几乎完全吻合，且高于数值结果；对于更为接近实际的非均匀扩张模式，精确解与数值解则拥有更高的吻合度，而简化解则整体偏小，但这种差异将随着浆泡埋深的增大而逐渐减小［7］。以上结果表明，在注浆抬升位移的预测中，对于浆泡均匀扩张模式，可采用简化方法近似计算，而对于非均匀扩张模式，采用精确方法将得到更为合理的结果。

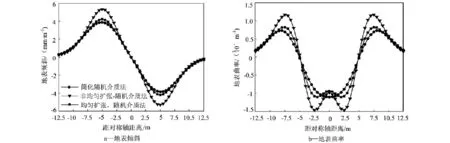
图5　双浆泡扩张引起的地表变形

此外，在非均匀扩张模式下（图5），地表倾斜峰值接近5．3mm／m，曲率峰值接近1．5×10－3／m。根据规范［10］关于地下开采中地表建筑物及其他保护对象等级的划分，当曲率大于0．6×10－3／m时，将引起建筑物发生Ⅳ级破坏，墙身将严重倾斜、错动，屋顶、墙身将被挤坏。尽管在建筑物抬升过程中，之前沉降引起的曲率将部分抵消注浆上抬的曲率，但在灌浆过程中仍需引起足够重视，加强现场监控，避免曲率过大反而使建筑物遭受破坏。

图6　地表水平位移

图6就数值法与简化法得到的地表水平位移进行了对比。可见，三种情况下的水平位移在曲线分布形态、峰值点位置和影响范围方面基本相同。其中，非均匀模式下的水平位移普遍大于均匀扩张模式，而简化解则介于两者之间。此外，注浆抬升引起的地表位移和变形形态与浆泡间距有着密切的关系。图7绘制了不同中心距条件下地表抬升位移分布曲线。当浆泡中心距不大时，双浆泡扩张引起的地表抬升规律与单浆泡扩张得到的结果非常类似，位移峰值位于两浆泡对称轴位置，抬升曲面为“单峰”形式；当浆泡中心距增大到10m时，地表抬升曲线呈现出“双峰”形态，最大位移不再处于对称轴位置，而是位于对称轴与浆泡形心轴之间。

图7　浆泡中心距对地表抬升位移的影响

3　结论

本文将注浆抬升效果视为地层中一连串浆泡径向扩张引起的效应之和，基于随机介质理论，推导出了多浆泡扩张下地表抬升变形的表达式及其简化解，验证了模型的合理性，并得到如下几点结论：

1）在注浆抬升位移的预测中，对于浆泡均匀扩张模式，简化解可得到较为合理的结果，而对于非均匀扩张模式，采用精确法求解则较为合理。

2）地表水平位移和倾斜曲线在分布模式和峰值点位置方面基本相同；且抬升过程中，应加强地表曲率的监测，避免曲率过大反而导致建筑物的破坏。

3）随着浆泡间距的增大，地表抬升位移逐渐由“单峰”形态过渡到“双峰”形态，峰值所在位置也逐

渐移动到对称轴与浆泡形心轴之间。

参考文献：

［1］ Wisser C，EAugarde C，Burd H J．Numerical modeling of compensation grouting above shallow tunnels［J］．International Journal for Numerical and Analytical Methods in Geomechanics，2005，29：443－471．

［2］ 唐智伟，赵成刚，张顶立．地下工程抬升注浆设计方法及其抬升效果预测研究［J］．土木工程学报，2007，40（8）：79－84．

［3］ 孙锋，张顶立，王臣，等．劈裂注浆抬升既有管道效果分析及工程应用［J］．岩土力学，2010，31（3）：932－938．

［4］ 张晓丽，张顶立，王梦恕．既有地铁注桨抬升合理位置的确定［J］．岩土工程学报，2008，35（8）：712－717．

［5］ 易小明，张顶立，逄铁铮，等．房屋注浆抬升实践与监测分析［J］．岩土力学，2009，30（12）：3776－3782．

［6］ 侯艳娟，张顶立，陈峰宾．隧道施工下穿建筑物注浆抬升机制及预测研究［J］．岩石力学与工程学报，2011，30（12）：2407－2415．

［7］ ZHANG Min，WANG Xinghua，WANG You．Mechanism of grout bulb expansion and its effect on ground uplifting［J］．Journal of Central South University of Technology，2011，18（3）：874－880．

［8］ Carter J P，Booker J R，Yeung S K．Cavity expansion in cohesive frictional soils［J］．Geotechnique，1986，36（3）：349－358．

［9］ Yang X L，Wang J M．Ground movement prediction for tunnels using simplified procedure［J］．Tunnelling and Underground Space Technology，2011，26（3）：462－471．

［10］ 韩煊，李宁，Standing J R．Peck公式在我国隧道施工地面变形预测中的适用性分析［J］．岩土力学，2007，28（1）：23－28．

［11］ 中华人民共和国煤炭工业部．建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程［S］．北京：煤炭工业出版社，1985．

（编辑：贾丽红）

Prediction and Simplified Model of Uplift Displacement by Grouting

ZHANG Min1，LIU Junjun1，QING Wenquan2
（1．College of Architecture and Civil Engineering，Taiyuan University of Technology，Taiyuan030024，China；2．Guangdong Electric Power Design Institute，Guangzhou510663，China）

Abstract：Ground heave caused by grouting was regarded as a random process，and assumed to be the sum of deformation due to the radial expansion of a series of slurry bubbles．According to the stochastic medium theory and linear superposition principle，a theoretical formula of ground heave，as well as its simplified form，was derived in uniform and non－uniform expansion mode．The comparison of different calculation methods demonstrates that while simplified solutions can effectively predict the surface uplift in the uniform expansion mode，the results obtained by the accurate method are more reasonable in the non－uniform mode．The results show that uplift displacement gradually transforms from unimodal to bimodal distribution with the increase of slurry bubble spacing，and horizontal displacement and tilt of the ground surface have basically the same curve shape and peak location．Moreover，it is necessary to strengthen the monitoring of surface curvature in the grouting process，and prevent the damage on surface buildings subject to excessive curvature．

Key words：grouting；ground surface uplifting；stochastic medium theory；simplified model

作者简介：章敏（1984－），男，江西新余人，博士，讲师，主要从事岩土工程方面的科研工作，（E－mail）zhangmin021410＠126．com

基金项目：国家自然科学基金资助项目：地震波作用下非饱和土中PHC管桩水平震动机理研究（51408393）；高等学校博士学科点专项

收稿日期：＊2014－11－24

文章编号：1007－9432（2015）03－0298－05

DOI：10．16355／j．cnki．issn1007－9432tyut．2015．03．010

文献标识码：A

中图分类号：TU45