位置误差对叉指状微小力装置力学特性影响分析

徐 立 ， 郑培亮 ， 李 闯 ， 黄振宇 ， 李 倩

（1.广东省现代几何与力学计量重点实验室，广东 广州 510405；2.广东省计量科学研究院，广东 广州 510405）

0 引 言

随着科技进步和工业发展，特别是微机电系统（MEMS）技术的广泛应用，微纳量级力学量应用不断增多，微小力量值溯源问题成为力学计量中前沿与热点问题之一。由于微小力量值溯源特殊性，目前世界各国仍处于研究阶段，并未建立相应量值溯源体系。对1cN～10N小力，应用中一般以标准砝码重力来进行量值溯源[1-3]。若力继续减小，采用微小标准砝码则误差过大，无法满足量值溯源要求。对mN、μN、nN量级微小力，多数研究人员采用静电力方法进行量值溯源，即通过电容器极板间产生微小静电力来测量或复现微小力[4-7]。

美国国家标准技术研究院（NIST）Pratt等[8]基于静电力原理，通过圆柱形电容器配合差动式平面干涉仪构建静电力天平，实现微小力量值溯源。德国国家物理实验室（PTB）Physikalisch等[9]设计差动式导电圆盘结构平行板电容装置，通过干涉式位移测量系统测出极板间位移变化，以测量小于10 μN的微小力。英国国家物理实验室（NPL）Leach等[10]同样基于圆柱形电容结构，利用平面镜差分干涉仪测量外力引起的介质片在四极板结构电容器间位移，来测量1nN～1 μN微小力。中国计量科学研究院Hu G等[11]采用圆柱状电容结合柔性铰链方式，配合激光干涉仪测量圆柱形电容内电极位移，实现微小力测量。

由此可见，基于静电力原理的电容式微小力装置中，极板间距与相对位置是决定输出微小力量值准确可靠的基础。针对位置误差对微小力装置影响，本文对一种新型叉指状微小力装置进行分析，该装置能大幅减少一定区间范围内位置误差对输出微小力影响，利用有限元分析方法对装置位置变化时输出力学特性进行分析。探讨装置在X、Y、Z方向平动及转动时，输出微小力变化规律。为该装置在微小力量值溯源中应用及简化微小力装置结构提供理论依据。

1 模型建立与位置分析

1.1 叉指电容器结构

如图1所示，新型叉指状电容由交叉放置的两叉指状电容极板构成。每个叉指电容极板包含若干根金属叉指，每根叉指都被固定于底座上。当处于图1所示位置时，两叉指（动叉指与定叉指）均与XOY平面平行，且XOY平面经过两叉指的中心平面。两叉指状电容极板间施加电压U时，将产生相互吸引的微小静电力。

采用高阶有限元方法对装置间静电场分布进行分析，主要研究装置间微小静电力。采用高阶有限元方法逼近真实解的优点是无需用户严格控制网格大小，即可获得要求准确度，且该方法自适应细分网格提供的误差估计比其他静电场分析方法更为准确，最重要一点是该方法能计算局部和总体场情况，并得到所需准确度结果，是计算本文所研究叉指间输出整体静电力最佳途径[15]。

图1 新型叉指装置结构图

1.2 装置位置分析

图1为理想状态下两叉指之间的位置，此时两叉指电容完全处于同一平面上，且各根叉指相互平行。

在实际使用中，由于距离测量以及位置控制误差的存在，两叉指电容不可能处于图1中完全理想状态。为了便于比较，本文在分析过程中假设定叉指处于理想状态且固定，且端面与YOZ平面重合，动叉指位置出现偏差。由图1可知，动叉指具有6个自由度，其可能发生位置偏移为沿X轴、Y轴、Z轴平移以及绕X轴、Y轴、Z轴旋转。

2 叉指平动对装置输出力学特性影响

2.1 动叉指沿X轴平动

动叉指由图1中理想状态位置沿X轴分别向X轴正方向移动12 mm及X轴负方向移动5.5 mm（若向X轴负方向移动6mm，两叉指电极将相互接触），装置输出力学特性如图2所示。图2（a）为装置输出微小力变化情况，由图可知，动叉指由理想位置向内（-X）或向外（+X）移动，两叉指间微小力均减小，但两叉指非常接近时（动叉指沿-X方向平移5.5 m），叉指间静电力急剧增大。在区域II内，装置输出微小静电力与理想位置基本相同。图2（b）为动叉指沿X轴运动时，装置输出微小静电力与理想状态输出静电力之间的误差。由图可知，动叉指在区域II内移动，装置输出微小静电力与理想状态误差＜2%。实际应用中，动叉指位置控制或测量出现误差，只需将位置误差控制在[-1 mm，4 mm]区间，即可保持装置输出微小力误差＜2%。

图2 动叉指沿X轴平动时输出微小力变化

2.2 动叉指沿Y轴平动

动叉指沿Y轴方向移动，装置输出微小力变化如图3所示。动叉指处于理想状态，输出微小力值最小，随着动叉指移动，输出微小力逐渐增大，动叉指与定叉指靠近，两叉指间静电力增速越来越大。由于装置结构对称性，动叉指向+Y方向与-Y方向移动，装置间静电力变化情况相同，图3呈对称分布。

图3 动叉指沿Y轴平动时输出微小力变化

由于动叉指与定叉指间在Y轴方向空间限制（本文研究参数下间距为1mm），动叉指沿Y轴方向移动距离被限制在[-1mm，1mm]区间范围内。由图 3（a）可见，动叉指移动范围在II区域时，输出微小静电力呈一条水平直线。图3（b）误差变化图也清楚反映这一特点。动叉指在区间II中移动，输出微小力与理想状态输出微小力误差在1.9%以内。应用中若动叉指沿Y轴位置测量或控制误差在[-0.2 mm，0.2 mm]区间，输出结果误差将小于1.9%。

2.3 动叉指沿Z轴平动

图4（a）为动叉指沿Z轴方向平移装置输出微小力特性变化。理想状态时，动叉指与定叉指之间正对面积最大，装置输出微小静电力最大。动叉指沿Z轴移动时，动叉指与定叉指间正对面积减小，装置输出静电力随之减小。动叉指移动距离超过0.5mm时，动叉指与定叉指已完全错开，此时装置输出静电力呈直线减小。图4同样可分为3个区域，动叉指处于区域II范围中，装置输出微小静电与理想状态相比输出值误差较小。图4（b）可见，动叉指位置偏移在[-0.2mm，0.2mm]区域，装置输出误差≤0.7%。由于动叉指沿Z轴移动0.5mm时，两叉指即完全错开，由图可知，动叉指在Z轴方向发生距离偏移40%时，对装置输出值影响在0.7%以内。

图4 动叉指沿Z轴平动时输出微小力变化

图2～图4比较分析可得，动叉指沿X轴偏移对装置影响较小，沿Y轴偏移对装置输出影响较大，应用中应重点关注Y轴方向位移测量与位置控制准确，保障装置输出微小力准确度。

3 叉指转动对装置输出力学特性影响

动叉指不仅能在X轴、Y轴、Z轴3个方向产生平动，也能绕3根坐标轴产生转动。动叉指转动时，装置输出微小力变化情况也是应用中需重点考虑的问题。

3.1 动叉指绕X轴转动

随着动叉指偏移理想状态绕X轴转动，两叉指间正对面积减小，装置输出静电力减小。图5横轴为动叉指绕X转动角度，正值表示绕X轴顺时针转动，负值表示绕X轴逆时针方向转动。“0”表示理想状态。由于装置结构对称，动叉指绕X轴顺时针和逆时针旋转对装置输出影响相同，图 5（a）和图 5（b）均以 0°为中心呈轴对称分布。图 5（b）可知，动叉指转动±1°，装置输出微小力变化仅为0.15%；转动±2°，输出微小力变化为1.02%。表明叉指位置控制误差在此区间内，装置输出微小力误差能控制在1.02%以内。动叉指转角继续增大，对装置输出影响也开始明显。当动叉指绕X轴转动7°时，输出微小力误差达到13%。

图5 动叉指绕X轴转动时输出微小力变化

3.2 动叉指绕Y轴转动

图6 动叉指绕Y轴转动时输出微小力变化

与绕X轴转动相同，动叉指由理想状态绕Y轴发生旋转，两叉指间正对面积减小，装置输出静电力减小，同时装置结构对称性使图6也以0°为中心呈轴对称分布。动叉指绕Y轴旋转对装置输出影响要明显小于绕X轴转动。图6可见，动叉指绕Y轴旋转10°，装置输出变化仍小于9%，且旋转角度在±5°内，装置最大输出变化仅0.25%，可认为若动叉指绕Y轴发生小角度偏移，对装置输出微小力几乎无影响。

3.3 动叉指绕Z轴转动

图7为动叉指绕Z轴转动时，装置输出微小力特性曲线。由图7（a）可知，图中微小力随旋转角度变化近似水平直线分布，表明动叉指绕Z轴转动对装置输出微小力影响较小。图7（b）误差分布图中在绕Z轴旋转±8°范围内，装置输出微小力值变化最大为1.11%，转角在±6°范围内时，装置输出误差≤0.5%。以上分析可知装置在绕Z轴方向发生旋转对装置的输出影响非常小。

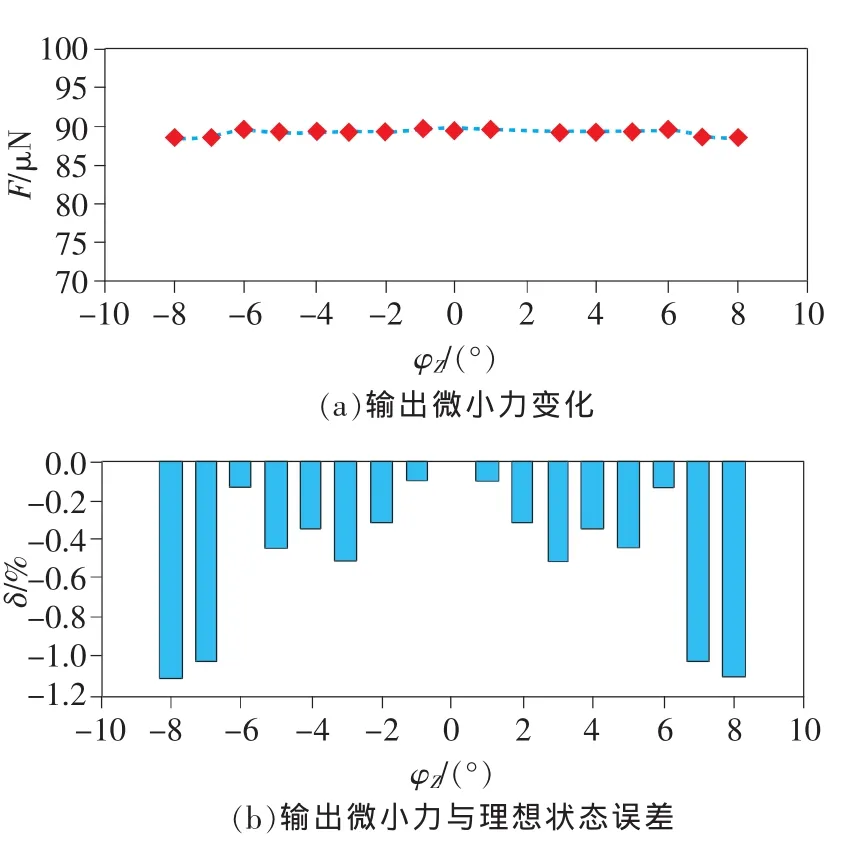
图7 动叉指绕Z轴转动时输出微小力变化

由图5～图7比较分析可得，动叉指绕X轴转动对装置输出有较大影响；绕Z轴转动对装置输出微小力影响较小。应重点控制装置位置绕X轴转动误差，以减小装置输出微小力误差。同时装置绕坐标轴转动所引起输出微小力值误差比平动时引起误差小。

表1 动叉指运动对装置输出影响较小区间

图8 动叉指复合运动偏移位置

3.4 动叉指复合运动时对装置输出影响

通过以上分析，动叉指位置测量与控制误差对装置输出微小力影响较小区间如表1所示。

实际应用中，装置位置测量和位置控制均可能出现误差，对装置输出结果产生影响。

为有效分析动叉指复合运动对装置输出微小力影响，本文对6个自由度影响较小区间内取极值进行分析。设动叉指沿X、Y、Z轴分别移动4，0.2，0.2mm，绕X、Y、Z轴分别转动 2°、5°、8°，此时位置如图 8 所示。图中所示位置偏移已十分明显，实际应用中只需对叉指位置稍加控制，便不会出现此种偏移。此时装置输出微小力85.903μN，与理想状态装置输出标准微小力误差为-4.10%，由此可见，装置在产生较大偏移时仍能保持较高输出准确度。

4 结束语

运用高阶有限元分析方法，对一种新型叉指状微小力装置沿X、Y、Z轴6个自由度上产生位置误差时，装置输出力学特性变化进行分析。结果表明：

1）动叉指在6个自由度上的位置误差均会对输出结果造成不同程度影响。

2）在每个自由度上，均存在一定区间范围，动叉指位置误差在该区间中时，对装置输出微小力影响较小。

3）动叉指沿X轴位置误差对装置的影响较小，沿Y轴位置误差对装置输出影响较大；绕X轴转动对装置输出有较大影响，绕Z轴转动对装置输出微小力影响较小。

4）装置绕坐标轴转动所引起输出微小力误差比平动时引起误差小。

5）装置在多个自由度上出现位置误差时，若误差范围在一定区间内，输出微小力误差较小。

6）该新型叉指状微小力装置能大幅减小一定区间范围内位置误差对输出微小力影响。

本文可为简化电容式微小力源装置设计与制造提供理论依据。

[1] Chen S J， Pan S S， Lin Y C.Comparison of milligram scale deadweights to electrostatic forces[J].Acta Imeko，2014，3（3）：68-72.

[2] Chen S J，Pan S S.A force measurement system based on an electrostatic sensing and actuating technique for calibrating force in a micro newton range with a resolution of nano-newton scale[J].Measurement Science and Technology，2011，22（4）：45-104.

[3] 齐永岳，刘明，林玉池，等.可溯源至质量的静电力复现与测量技术[J].仪器仪表学报，2011，32（5）：1063-1068.

[4] Kim M， Pratt J R.SI traceability：Current status and future trends for forces below 10 micro newtons[J].Measurement，2010，43（2）：169-182.

[5] Stefǎnescu D M， Anghel M A.Electrical methods for force measurement-A brief survey[J].Measurement，2013，46（2）：949-959.

[6] Kim M S， Pratt J R， Brand U， et al.Report on the first international comparison of small force facilities：a pilot study at the micro Newton level[J].Metrologia，2012，49（1）：70.

[7] Pratt J R，Kramar J A，Newell D B，et al.Review of SI traceable force metrology for instrumented indentation and atomic force microscopy[J].Measurement Science&Technology，2005，16（11）：2129-2137.

[8] Pratt J R，Kramar J A.SI realization of small forces using an electrostatic force balance[C]∥Proc.XVIII IMEKO World Congress on Metrology for a Sustainable Development，2006：109.

[9] Physikalisch T， Bundesanstalt B， Berlin B.Facility and methods for the measurement of micro and nano forces in the range below 10-5N with a resolution of 10-12N[J].Measurement Science and Technology，2007（18）：360-366.

[10]Leach R， Blunt L，Chetwynd D， et al.Recent advances in traceable nanoscale dimension and force metrology in the UK[J].Measurement Science&Technology，2006，17（3）：467-476.

[11]Hu G， Song L， Meng F， et al.Research and development of small force standards at NIM[C]∥International Journal of Modern Physics：Conference Series.World Scientific Publishing Company，2013（24）：1360020.

[12]蔡雪，赵美蓉，郑叶龙，等.用于10-6N～10-5N微力测量的柔性铰链机构设计[J].传感技术学报，2014（11）：1451-1456.

[13]刘明，林玉池，郑叶龙，等.利用静电场原理复现微小力值的实验研究[J].传感技术学报，2012，25（1）：33-37.

[14]Munz M.Force calibration in lateral force microscopy:a review of the experimental methods[J].Journal of Physics D Applied Physics，2010，43（6）：63001-63034（34）.

[15]徐立，郑培亮，李倩，等.叉指状微小力装置力学特性的数值模拟与分析[J].中国测试，2015，41（9）：115-119.