基于MCMC的导弹多阶段可靠性评估*

朱会传 徐廷学 董 琪

(1.海军航空工程学院研究生管理大队 烟台 264001)(2.海军航空工程学院兵器科学与技术系 烟台 264001)



基于MCMC的导弹多阶段可靠性评估*

朱会传1徐廷学2董 琪1

(1.海军航空工程学院研究生管理大队 烟台 264001)(2.海军航空工程学院兵器科学与技术系 烟台 264001)

针对导弹在研制试验中存在多阶段、样本量小而造成传统评估误差大的问题,建立了基于模糊理论、Bayes方法和马尔可夫链蒙特卡罗法(MCMC)的可靠性评估模型。根据专家信息和模糊理论确定可靠性先验分布;并利用Bayes公式得到可靠度后验分布函数;结合试验多阶段的特点,通过MCMC模型对不同阶段导弹的可靠性进行评估,其中利用Gibbs抽样算法对模型进行求解。通过算例分析,验证了模型的有效性,为可靠性增长评估提供了新的思路。

可靠性评估; 仿真; 马尔可夫; 蒙特卡罗

Class Number TP182

1 引言

导弹系统是复杂的武器系统,对可靠性要求较高,对其进行可靠性评估是研制工作的客观需求和重要内容[1]。

由于导弹中主要部件像发动机和引信这类结构复杂的系统,研制成本较高,在试验中会产生样本量不大的专家信息和成败型试验数据。在对这样的系统进行可靠性评估时,传统的可靠性理论适用性不强。

Bayes方法在可靠性多源信息融合中有着广泛的应用。现有的Bayes可靠性增长模型主要为Smith模型[2]、Bar-Scheuer模型[3]、折合因子法[4]等,而且同样运用Bayes方法,文献[5]主要融合了产品验前信息和现场信息进行进精度鉴定;文献[6]则注重多维动态参数的融合来分析飞行器的试验中的可靠性;文献[7]综合利用专家信息和各实验阶段的信息,并基于狄氏分布和可靠性增长来分析固体火箭发动机可靠性;文献[8]主要利用性能退化数据进行可靠性评定;文献[9]利用发动机运行数据和地面试验数据进行可靠性分析。

不同的装备性能的变化有着不同的规律,需要用不同的模型来进行分析。本文针对导弹在研制过程出现的试验数据的特点,给出一种综合利用模糊理论、Bayes方法和MCMC(Markov Chain Monte Carlo)方法,融合可靠性先验信息和小样本现场试验信息的可靠性建模与分析方法,充分利用研制阶段的多重信息,在很大程度上提高了可靠性评估的精度。本文研究思路如下:以导弹的关键部件发动机为例,首先根据利用模糊理论对专家信息进行赋值,确定先验分布参数,进而拟合出成败型系统先验分布函数;然后结合Bayes、可靠度联合先验密度函数及可靠度似然函数得到可靠度后验分布函数;最后,利用MCMC算法中最有代表性的Gibbs抽样算法对模型进行求解计算。

2 确定先验参数

先验参数的求解是确定先验分布的关键,也是利用Bayes进行可靠性评估的难点和重点[10]。通常情况下,先验参数的确定依据来自专家经验或者相似产品信息等,而且应优先参考相似产品信息,当无相似产品信息时,再由专家经验给出先验信息。但是由于导弹在研制阶段,缺少相似产品的参考信息,所以采用专家经验来计算先验信息。由于不同的专家给出的先验信息的可信度不同,本文对不同专家给出的先验信息附加不同的权重值,使获得的先验信息更科学、合理。

根据专家给出的可靠度区间,宜采用均匀分布进行描述,求出与该均匀分布最为接近的Beta分布,作为先验分布。步骤如下:

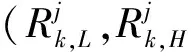
然后,利用模糊理论对专家信息进行权重分配,可先构造模糊判断矩阵。可以从专家从事相关研究的时间、职称、职务等方面综合考虑,并采用0～1七标度构造互补模糊矩阵,0～1七标度表示不同专家两两相对重要程度,含义如表1所示,其中X、Y表示两个不同的专家。

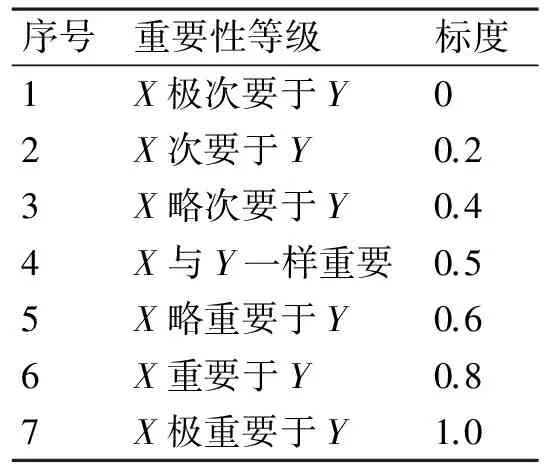
表1 模糊判断矩阵标度及其含义

接着,计算相应权重向量。方法如下:

1) 将模糊互补矩阵M(mik)l×l按式(6)求和

(1)

2) 通过式(7)得到模糊一致矩阵MT(tij)l×l

(2)

3) 由式(3)对矩阵MT(tij)l×l行和归一化即可得到不同专家先验信息的影响权重排序向量w=(w1,w2,…,wl)T。其中第i个专家的权重值为

(3)

最后,根据权重排序和l个专家的先验信息,利用式(3)经过加权综合得到第k个试验阶段的可靠性先验信息。

(4)

该试验阶段可靠性先验信息的均值和方差为

(5)

令先验信息均匀分布的均值和方差与先验Beta分布的均值和方差等价,通过解方程可确定先验参数值。因此需要求出在已知前k-1个试验阶段可靠度的条件下,第k个试验阶段可靠度条件均值和条件方差为

(6)

由于在实际计算得到的先验参数有时会出现负值,不能满足先验参数都为正值的要求,针对这种情况,可建立最优化模型,如式(7)～式(9),将均值作为约束,方差作为目标,确定第k个试验阶段最优先验参数。

目标函数为

min(vk-VRk)2

(7)

约束条件为

μk=ERk

(8)

ak>0bk>0

(9)

其中式(6)中Rk-1可由第k-1个试验阶段的条件均值μk-1代替。

3 基于MCMC预测模型的建立

马尔可夫链预测模型对未来状态的预测,不需要寻求系统复杂因素之间的相互规律,只需考虑系统本身历史状态的演变特点,是一种动态随机数学模型。

3.1 模型建立

由调研和分析知道,导弹在研制过程中,多是在出现故障后进行故障的维修,而在两次故障期间,可靠性水平依次降低,该趋势称为序化约束模型。如式(10)所示:

0≤R1≤R2≤…≤Rk≤…≤Rm≤1

(10)

其中,Rk为第k个时间点的可靠性水平。

构造第k个时间阶段的可靠度先验分布函数,即fk(Rk|Rk-1) =fk(Rk|Rk-1;ak,bk)

×(1-Rk-1)1-ak-bkI(Rk-1,1)(Rk)

(11)

式中B(ak,bk)是先验参数为ak和bk的Beta函数,且ak>0,bk>0,令R0=0,Rm+1=1。

综合各试验阶段的可靠度分布函数可得联合先验密度函数

(12)

式中R=(R1,R2,…,Rm)为各试验阶段可靠度估计值。

根据不同试验阶段的试验数据可以确定可靠度似然函数,若在第k个试验阶段现场数据为(nk,sk),其中nk表示第k个试验阶段的总试验数,sk表示第k个试验阶段的总成功数。则可靠度Rk的似然函数为

(13)

整个试验阶段可靠度R的似然函数为

(14)

3.2 可靠度后验推断

确定先验参数后即可确定先验分布函数,由式(12)和式(14),结合Bayes公式可得R的后验分布为

×(1-Rk-1)1-ak-bk

(15)

在计算后验分布和后验估计时,会面临难以求解的高维积分问题。而MCMC方法已成为一种处理复杂统计问题的有效工具,更经常应用于需要复杂高维积分的Bayes分析领域。Gibbs抽样是一种MCMC算法[11],它将随机过程中的马尔可夫链应用到蒙特卡罗模拟中。本文采用Gibbs抽样算法进行后验积分和后验估计的计算。利用Gibbs抽样方法产生随机样本的步骤如下:

1) 抽样时,可由式(15)经过推导得R的后验密度的核

×(1-Rk)bk+nk-sk-ak+1-bk+1

(16)

2) 确定完全条件分布。对于后验密度的核,在给定Rk-1的情况下,fk(Rk|Rk-1;ak,bk)仅为Rk的分布函数,因此,fk(Rk|Rk-1;ak,bk)显然是参数Rk的完全条件分布。

…

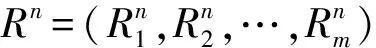
将需要计算的后验估计写成函数φ(Ri)关于后验分布fk(Rk|Rk-1;ak,bk)的期望:

E[φ(Ri)]=∫φ(Ri)fk(Rk|Rk-1;ak,bk)dRi

(17)

4) 判断收敛性。模型是否收敛常根据迭代图形来判断,即同时输入多组初始值经过一段时间的Gibbs抽样后,通过迭代图形结果判断,若迭代图形趋于重合,则认为Gibbs抽样收敛。

根据后验分布式(17)得到完全条件分布为

×(1-Rk)bk+nk-sk-ak+1-bk+1

(18)

此时,对完全条件分布式(17)进行标准取舍抽样,令

×(1-Rk)bk+nk-sk-ak+1-bk+1

(19)

g(Rk)∝(Rk-Rk-1)ak-1(1-Rk)ak+1-1

(20)

可见g(Rk)为区间(Rk-1,1)上的截尾Beta分布,易于从g(Rk)抽样。

利用Gibbs算法得到R的抽样值后,就可以利用这些抽样值对Rk的后验估计和后验区间进行推断。

4 实例分析

在导弹发动机研制过程中,使用人员制定了四个可靠性增长试验阶段。首先,由于未找到相似产品信息,现只提取专家信息。本次专家信息提取的调查对象,是对该装备使用过程和可靠性较熟悉的专家,参加调查的共有五位专家,分别来自研制部门、基层部队和相关院校。在职称方面,高级工程师三名,工程师二名;学历方面,博士二名,硕士三名。工作年限,高级工程师一般在21～30年,工程师一般在11年～20年。

本次专家信息的提取方式采用调查问卷方式。其中,专家信息主要是统计学描述方式,即置信区间形式,如表2所示。

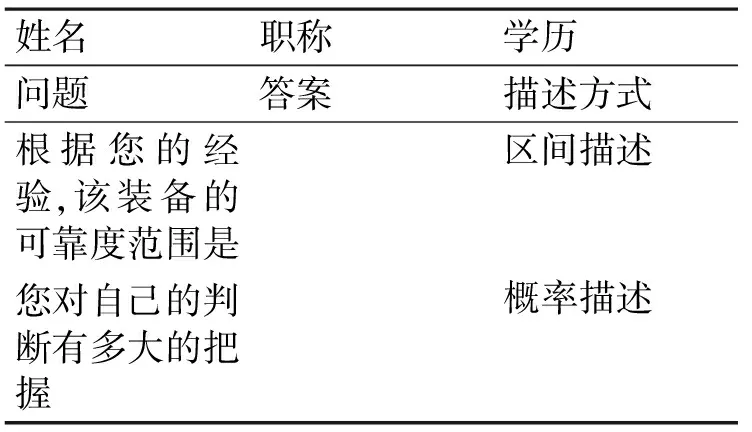
表2 发动机可靠度专家信息调查表

本次调查表一共发放20份,收回有效问卷20份,下面对专家信息进行处理。

首先,根据专家信息调查表构造模糊互补矩阵M:

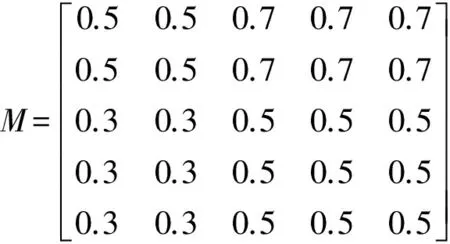
根据式(2)得到模糊一致矩阵MT:

由式(3)对矩阵MT行和归一化得到专家先验信息影响权重排序向量w=(0.2188,0.2188,0.1875,0.1875,0.1875)T。

其次,对专家给出的可靠性信息进行加权得到不同阶段可靠性先验信息,并结合试验数据如表3所示。

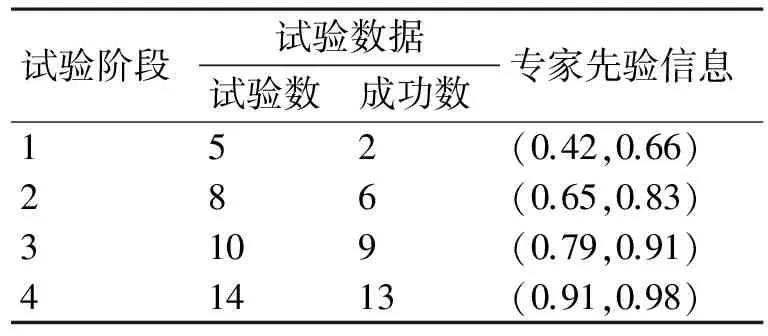
表3 发动机先验信息和试验数据

再次,利用式(7)～式(9)可以得到各试验阶段与均匀分布等价的Beta分布的先验参数ak和bk,如表4所示。

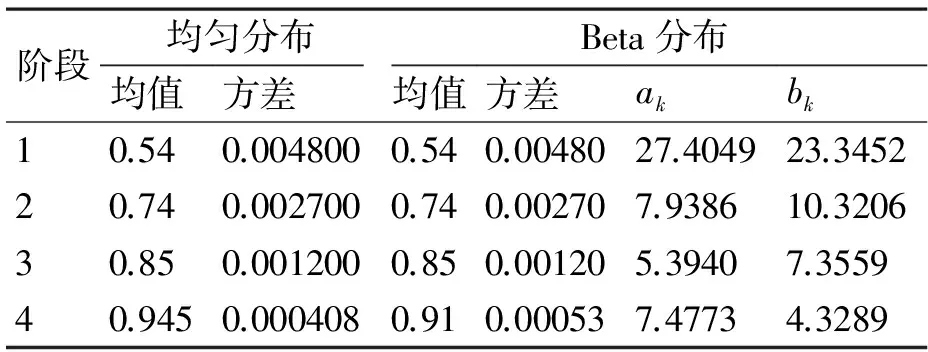
表4 Beta分布先验参数

确定先验参数后,即可将试验数据与先验参数代入式(16),利用Gibbs抽样计算导弹发动机可靠度,采用三个不同的初始值并产生三条Markov链,迭代次数取10000次,然后观测三条Markov链的抽样值,并判断收敛性。

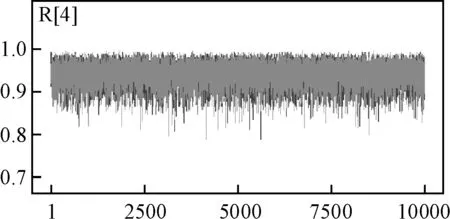
图1 R[4]的三条Markov链的抽样值

如图1所示,第四试验阶段发动机可靠度R[4]的三条Markov链迭代图形结果趋于重合,说明抽样值随着迭代次数的增加趋于稳定。图2～图4显示了R[4]的迭代轨迹、分位数、核密度等抽样信息,而如图5所示,R[4]的自相关函数很快接近于0,也证明迭代过程已收敛。

图2 R[4]的迭代轨迹图

图3 R[4]的分位数

图4 R[4]的核密度函数图

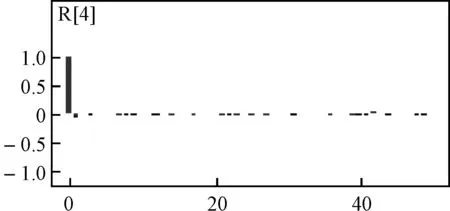
图5 R[4]的自相关函数

通过Gibbs抽样,得到各试验阶段可靠性的后验估计结果,如表5所示。

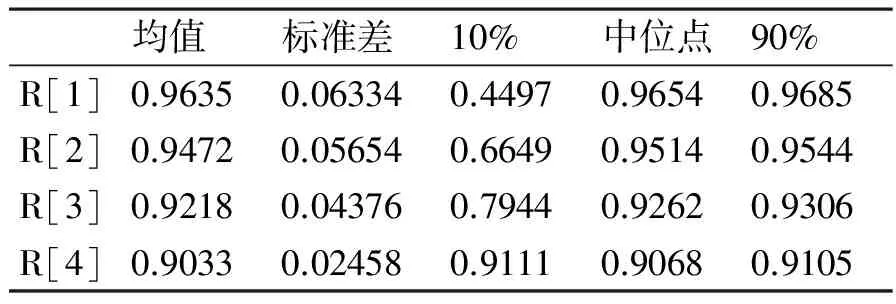
表5 发动机各试验阶段可靠度的后验估计

若仅利用第四阶段的试验数据,得到的可靠度估计值为0.9286,略低于0.93的要求值,且受样本量影响较大。由表5可见,导弹发动机在试验结束后的可靠度估计值为0.9433,基本满足了0.93的可靠性要求,这是因为本文采用的方法利用先验信息以及前阶段的可靠性信息,利用的可靠性信息更多,得出的结果更真实可靠。

5 结语

针对导弹研制过程成败型数据样本量小的特点,给出一种综合利用模糊理论、Bayes方法和MCMC方法的可靠性建模与分析方法,充分利用了可靠性先验信息和小样本现场试验信息,在一定程度上提高了可靠性的计算精度。实例分析表明,该方法对研制阶段导弹的可靠性评估是有效和可行的。

[1] 周忠宝,厉海涛,刘学敏,等.航天长寿命产品可靠性建模与评估的Bayes信息融合方法[J].系统工程理论与实践,2012,32(7):2517-2522.

[2] Smith A F M. A Bayesian notes on reliability growth during a development testing program[J]. IEEE Transactions on reliability,1977,(26):346-347.

[3] Barlow R E, Scheuer E M. reliability growth during a development testing program[J]. Technometrics,1966,(8):53-60.

[4] 田国梁.二项分布的可靠性增长模型[J].宇航学报,1992,(1):55-61.

[5] 张金槐.多源信息的Bayes融合精度鉴定方法[J].国防科技大学学报,2001,23(3):93-97.

[6] 张金槐.多维动态参数的多层Bayes融合设计[J].国防科技大学学报,2003,25(4):97-101.

[7] 刘飞,窦毅芳,张为华.基于狄氏先验分布的固体火箭发动机可靠性增长Bayes分析[J].固体火箭技术,2006,29(4):239-242.

[8] 冯静,刘琦,周经伦,等.基于性能退化数据的液体火箭发动机可靠性Bayes分析[J].航空计算技术,2003,33(3):6-10.

[9] 刘琦,冯静,周经伦.火箭发动机性能可靠性的Bayes分析[J].中国空间科学技术,2003,23(6):46-51.

[10] 白璐.可靠性评估中的一种Bayes方法[J].质量与可靠性,2007,129(3):20-23.

[11] 张云安.小样本复杂系统的多阶段可靠性增长评估与可靠性鉴定[D].长沙:国防科技大学,2008:100-102.

Multi-stage Reliability Assessment of Missile Based on MCMC

ZHU Huichuan1XU Tingxue2DONG Qi1

(1. Graduate Students’ Brigade, Naval Aeronartical and Astronautical University, Yantai 264001)(2. Department of Weapon Science and Technology, Naval Aeronartical and Astronautical University, Yantai 264001)

The reliability evaluation model based on fuzzy theory, Bayesian analysis method and MCMC is established for solving the problem of the small sample of missile reliability and mulit-stage during the development of the missile. According to the expert information and fuzzy theory, the prior distribution of reliability is determined. The posterior distribution is given by making use of the Bayesian formula. The reliability assessment of the every stage of the missile equipment is verified by sampling simulation of Markov Chain Monte Carlo and Gibbs Calculate method. Finally, an example is used to illustrate the effective of the model, and provide a new method for the reliability-growth assessment.

reliability assessment, simulation, Markov, Monte Carlo

2014年9月1日,

2014年10月19日

朱会传,男,硕士研究生,研究方向:武器装备综合保障理论与技术。徐廷学,男,博士,教授,研究方向:武器装备综合保障理论与技术。董琪,男,博士研究生,研究方向:武器装备综合保障理论与技术。

TP182

10.3969/j.issn1672-9730.2015.03.027