高面膜堆石坝运行状态下土工膜双向拉伸力学特性——高面膜堆石坝关键技术(三)

吴海民，束一鸣，姜晓桢，任泽栋

(1．河海大学水利水电学院，江苏南京 210098;2．水文水资源与水利工程科学国家重点实验室，江苏南京 210098;3．南京水利科学研究院岩土工程研究所，江苏南京 210029;4．山东省水利勘测设计院，山东济南 250013)

土工膜是一种平面形状的高分子柔性材料，在防渗体内部多处于平面受力状态，其主应力更接近双向拉伸应力状态。对于土工膜上游面(简称“面膜”)防渗堆石坝，一般在坝体填筑完成时沿坝坡铺设土工膜，此时堆石坝体大部分竖向沉降已完成，土工膜主要由蓄水引起坝体向下游垂直于坝面的位移而产生变形，这种变形会使土工膜由原来的平面形状变成向下游凸出的锅面形状，土工膜因承受沿坝坡和坝轴线两个方向的拉力而处于双向受力状态。此外，在坝面周边锚固处的极小区域内，土工膜同时受到坝体沉降与向下游位移的影响也会产生双向拉伸应力，尤其在岸坡和坝基交汇点拐角处，土工膜受到双向拉伸和“夹具效应”双重作用而极易发生破坏。

目前土工膜防渗技术在我国虽然得到了广泛的应用和发展，但对土工膜运行状态下力学特性的研究尚不够深入。在过去二三十年间，国内外学者对土工膜的力学特性做过大量研究工作。束一鸣等［1-5］对不同PVC、PE光膜和复合土工膜的拉伸力学特性进行了一系列试验研究，获得了不同土工膜拉伸受力变形规律和基本力学参数;胡利文等［6］采用光学显微镜和电镜对在各种不同延伸率下土工膜的微结构进行了分析;徐光明等［7］对损伤土工膜的拉伸力学特性进行了试验研究。以上研究主要集中在土工膜的极限强度和延伸率等力学性能参数上。国外学者则在土工膜应力-应变关系方面做了大量的研究工作，Giroud［8］用窄条拉伸试验方法研究了土工膜的应力-应变关系;Merry等［9］通过液胀多轴拉伸试验得到双曲线形式的土工膜应力-应变关系方程;Zhang等［10-13］分别用不同试验方法给出了各种形式的基于拉伸应变速率的土工膜应力-应变关系黏弹性模型，但这些模型都比较复杂，模型参数计算也不方便，需要进行专门的试验，所以并未成为工程师们设计时所能采用的实用模型;Wesseloo等［14］用宽条拉伸试验方法得到了基于应变率的土工膜应力-应变关系分段函数模型;Giroud［15］通过理论分析指出土工膜泊松比并非常数，而是随延伸率的增加不断降低，并推导出土工膜泊松比随应变变化的数学表达式。通过总结可以发现上述有关土工膜力学特性的研究成果虽然较多，但所采用的试验方法主要有两类，即条带拉伸试验和液胀多轴拉伸试验。条带拉伸试验又分为单向窄条拉伸试验和单向宽条拉伸试验［16-17］。3种方法的主要区别在于试验过程中试样的受力状态不同。条带拉伸试验中，试样呈单向拉伸应力状态，试样变形无侧向限制，与材料在工作中实际平面受力状态相差较大，拉伸时容易出现“颈缩”现象而导致材料的延伸率易被高估［18］;液胀多轴拉伸试验中，锚固环附近试样处于平面应变状态，液胀膜球顶部试样呈双向等值拉伸应力状态［19］。对于土工膜而言，液胀多轴拉伸试验相比条带拉伸试验能更好地反映实际工程中土工膜真实工作中的应力状态，但土工膜液胀后的应力和应变均无法直接测试，目前是在假定土工膜液胀后变形为球面的基础上采用几何方法推导出液胀压力与土工膜应力-应变关系。但由于在液压作用下，土工膜变形挠度曲线上各点厚度和曲率并非恒定值，所以，这种假定会导致得到的真应力-真应变关系曲线产生较大误差［18］，而且试验中双向应力比例及应力历史和路径均无法控制，只能进行等值双向拉伸。此外，试验中土工膜的应力和应变加载速率也较难控制，所以该试验方法未得到推广应用。

现有土工膜力学特性试验方法的缺陷及局限性导致土工膜试验过程中的应力变形状态与实际运行性态不一致。目前常用的条带拉伸试验方法得到的力学特性只能用于不同土工膜产品指标参数的横向比较，无法用于工程设计计算;此外，试验得到的应力-应变关系为名义应力(拉伸力除以横截面初始面积)与名义应变(两个拉伸夹具之间距离的伸长率，即整个试样的平均应变)的关系，也无法直接用于土工膜受力变形性态的数值分析与安全评价。所以至今尚无土工膜设计的应力安全系数和应变安全系数规范，这在一定程度上限制了土工膜防渗高坝的建设和发展。为揭示堆石坝面防渗土工膜实际运行中的受力变形特性，准确预测土工膜受力变形性态及安全度，有必要研发土工膜双向拉伸试验设备及试验方法，对最接近其运行形态的双向拉伸力学特性进行系统深入的研究。

1 双向拉伸试验装置及方法

为了对土工膜双向拉伸力学特性进行试验研究，笔者及其所在研究团队自主研发了2套土工膜双向拉伸试验装置并获得国家发明专利授权［20-22］。

1．1 “十”型双向拉伸试验装置及方法

图1为自行研制的“十”型土工膜试样双向拉伸试验机，该设备既能进行复杂应力、应变路径下瞬时双向拉伸试验，又能进行双向拉伸下长期蠕变试验;试样尺寸大，拉伸行程长，能进行柔性材料的大变形试验，试验效率高，具有长期可靠性和稳定性［21］。

如图1(a)所示，“十”型双向拉伸试验主要是通过4个夹具夹住试样的四肢，通过试验机提供的拉伸荷载使试样中心发生双向拉伸变形，从而在试样中心区形成双向受力状态。试样受到的拉伸力通过与夹具相连的4个拉力传感器测得，4个方向上的变形通过安装在夹具尾部的位移计测得，通过计算机软件控制和数据采集系统就可测得双向拉伸力-位移曲线。

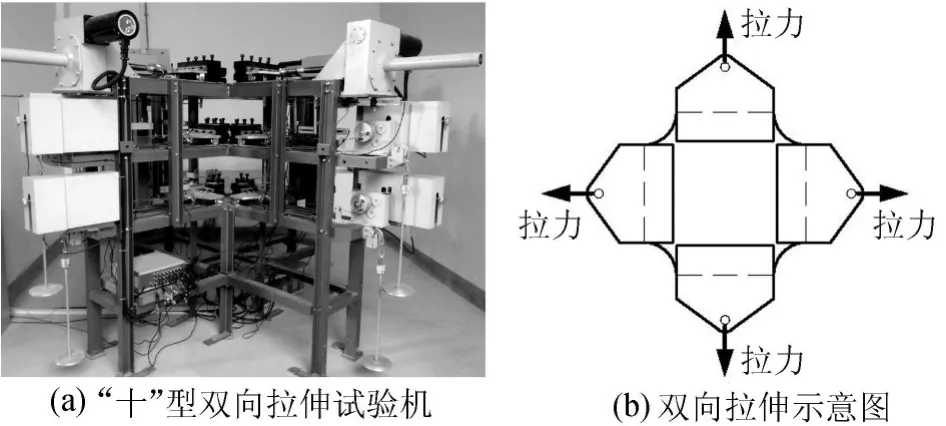
图1 “十”型土工膜试样双向拉伸试验装置

与常规土工膜单向拉伸试验相似，在双向拉伸过程中，整个试样区域内的变形并非完全均匀，通过安装在夹具端部的位移传感器可测得两个夹具间距离的变化，但无法测得土工膜局部真实变形分布。对于“十”型双向拉伸，目前尚无成熟的应变测试和计算方法。本文采用图像分析法进行土工膜局部真应变的测试，即试验过程中采用高清摄像机采集试样中心标记区网格的变形过程，然后通过图像处理分析中心点附近4个网格的变形得到试样中心2个方向上的真实应变，并通过广义虎克定理计算出泊松比［23］。在双向拉伸过程中，试样中心区的真应力也无法直接测得，试验中首先采用数值分析和理论推导相结合的方法获得不考虑中心区截面积变化的名义应力，然后根据高分子材料体积不变理论，利用测得的试样中心区双向真应变推导试样截面厚度和截面积变化，进而得到考虑截面积变化的真应力修正系数，然后通过对名义应力进行修正得到试样中心区截面的真应力［23］。试验过程中得到土工膜真应力和真应变后，即可获得双向拉伸真应力-真应变关系。

1．2 “筒”型双向拉伸试验装置及方法

图2为筒型土工膜试样双向拉伸试验装置。试验中将“筒”型土工膜试样上下两端固定在2个圆盘形的夹具上，借助于万能试验机提供轴向拉伸荷载进行轴向拉伸，同时使用气泵通过夹具上预留的通气孔向圆筒试样内部充气以提供内压，试样在两端拉伸荷载和内压作用下由筒状变形为鼓状，在试样中间部位形成双向拉伸受力状态。

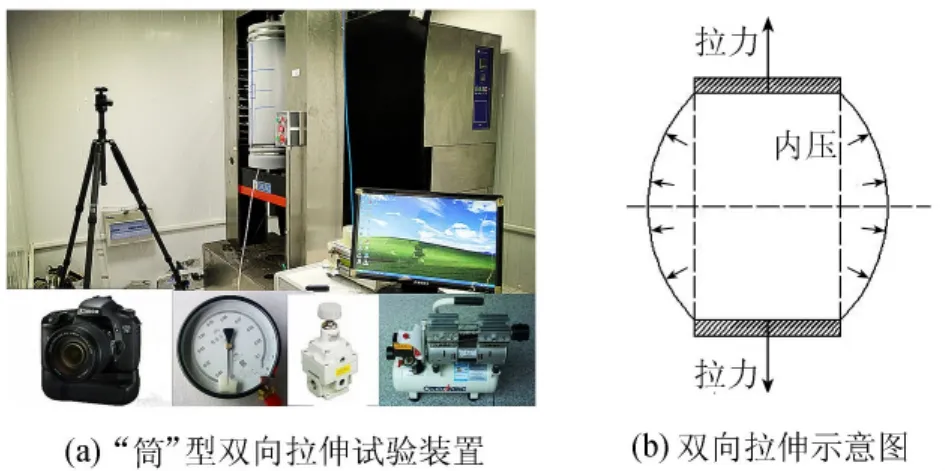
图2 “筒”型土工膜试样双向拉伸试验装置

在土工膜“筒”型双向拉伸试验中，试样轴向拉伸力和拉伸变形可以通过万能试验机的测力传感器和位移计测得，环向拉力可由精密气压表测得试样内压再进行理论计算得到［22］，环向变形通过高清摄像机测量试样外轮廓变化图像然后进行处理分析得到，这样就可以得到轴向和环向拉伸力-位移曲线。此外，同“十”型双向拉伸试验方法一样，采用图像分析法进行土工膜局部真应变的测试，可以得到试样中间标记区的双向真应变，同时根据理论推导得到该标记区厚度和截面积变化，结合名义应力可计算出真应力，进而获得试样中间部位标记区的真应力-真应变关系。

2 试验方案及材料

2．1 试验方案

本文研究主要针对大坝防渗中常用的PE、PVC和HDPE光膜。具体试验方案如下:首先，采用“十”型双向拉伸试验方法对目前国内中低坝防渗使用最多的PE膜进行了单、双向拉伸对比试验，拟揭示堆石坝面防渗土工膜的变形特性和破坏机理，进一步证明进行双向拉伸试验研究的必要性。一共进行单向条带拉伸、双向等速拉伸、双向不等速拉伸和侧向限制拉伸4组试验。其次，采用“十”型双向拉伸试验方法针对国外高坝常用的PVC膜和我国目前最高面膜堆石坝(仁宗海堆石坝)所采用的HDPE膜分别进行双向拉伸试验研究，揭示高堆石坝面膜运行下的双向拉伸力学特性及真应力-真应变关系;针对两种材料分别进行了双向等速拉伸、不等速拉伸和侧向限制拉伸情况下的6组试验。再次，采用“筒”型双向拉伸试验方法针对国内中低坝防渗使用最多的PE膜的双向拉伸力学特性进行了研究，揭示PE膜双向拉伸真应力-真应变关系。共进行了内压分别为 20 kPa、30 kPa、40 kPa、50 kPa 和60 kPa情况下的5组试验。

以上试验均在恒温恒湿环境进行。环境温度控制在(25±2)℃，湿度在50% ～70%。“十”型双向拉伸试验的纵向及“筒”型双向拉伸试验的轴向均采用1%/min应变率的拉伸速率进行。

2．2 试验材料

试验中的PVC和HDPE膜均为1.5 mm厚的光膜，PE膜为1.0 mm厚的光膜。“十”型双向拉伸试样有效尺寸为300mm×300mm，“筒”型双向拉伸试样内径为300 mm，长为450 mm。几种典型试样如图3所示。

图3 土工膜双向拉伸试样

3 试验结果

3．1 PE膜单、双向拉伸试验结果

图4为PE膜单向及不同双向拉伸条件下拉伸力随名义应变的变化曲线。由图4可知，不同试验条件下的拉伸强度从大到小顺序为:双向等速拉伸强度、双向不等速拉伸强度、侧向限制拉伸强度、单向拉伸强度，弹性模量的大小顺序也相同。所以，对于PE土工膜而言，双向拉伸强度和弹性模量要大于单向拉伸强度。而延伸率正好相反，单向拉伸延伸率大于双向拉伸延伸率。可见，传统单向拉伸试验会导致土工膜强度和模量被低估，而延伸率被高估。

图4 PE膜单、双向拉伸曲线

图5为PE膜单向拉伸和“十”型双向拉伸变形破坏状态对比。由图5可知，单向拉伸试样在100%应变下尚未破坏，而双向拉伸试样在30%应变时已经发生严重破坏。这说明实际工作状态下的土工膜延伸率并非很高，其变形能力被高估。双向拉伸试样随着试样被夹持的四肢拉伸位移的不断增大，试样中心区也发生了较大变形，但屈服破坏首先从试样四角开始，并沿着对角线向试样中心发展。

图5 PE膜单、双向拉伸变形破坏状态

3．2 PVC和HDPE膜“十”型双向拉伸试验结果

3．2．1 PVC 膜试验结果

图6为PVC膜在3种双向拉伸条件下的变形状态。由图6可知，在双向拉伸条件下，PVC膜中心区发生明显的双向拉伸变形，并处于双向不同应力比例的受力状态。同时也可以看出，PVC膜具有很强的变形能力，在双向等速拉伸(纵、横向应变均达到35%)，双向不等速拉伸(纵向应变28%、横向应变42%)，侧向限制拉伸(纵向应变80%、横向固定)3种条件下均未发生拉伸破坏。

图6 典型双向拉伸条件下PVC膜变形状态

图7为PVC膜单向和3种不同双向拉伸状态下真应力随真应变的变化曲线。由图7可知，单、双向拉伸下PVC膜2个方向上的真应力与真应变均呈近似的线弹性关系，真应力均随真应变的增大而增大。相同应变下，单向拉伸的真应力小于双向拉伸的真应力;相同应力下，单向拉伸应变大于双向拉伸应变。

本报讯 工业和信息化部日前对申请立项的410项行业标准计划项目和64项国家标准计划项目予以公示并征集意见，其中包括《化肥追溯体系规范》化工推荐性行业标准制定项目。征集意见截止时间为11月28日。

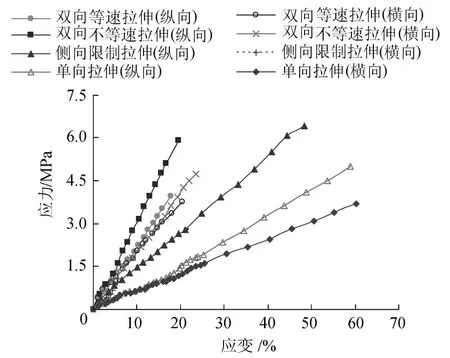
图7 PVC膜单、双向拉伸真应力-真应变关系曲线

表1为不同拉伸条件下5%、10%和20%这3个纵向名义应变对应的纵、横向弹性模量值。由表1可见，PVC膜弹性模量与应力状态有关，单向拉伸弹性模量远小于双向拉伸弹性模量;弹性模量还与不同双向拉伸比例有关;此外，PVC膜纵、横向弹性模量间存在差异，差异与不同拉伸条件有关。

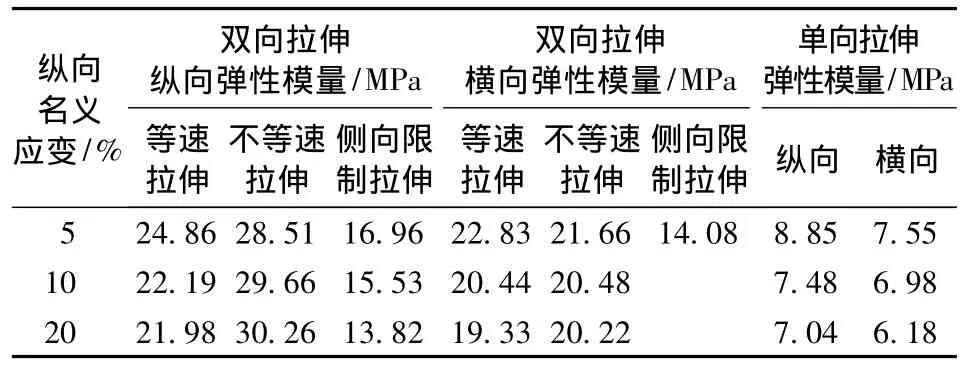
表1 PVC膜单、双向拉伸下特征应变对应的弹性模量

图8为单、双向拉伸状态下PVC膜泊松比随纵向名义应变的变化曲线。由图8可知，单、双向拉伸状态下PVC土工膜的泊松比均随着纵向名义应变的增大而减小，且减小的幅度越来越小;单、双向拉伸状态下泊松比也有一定差异。说明PVC膜泊松比不仅与应变大小有关系，还与单、双向拉伸状态有关。对于相同纵向名义应变下的泊松比，单向拉伸的值要小于3种双向拉伸结果，并且单、双向拉伸的差异随着应变的增大也越来越大。

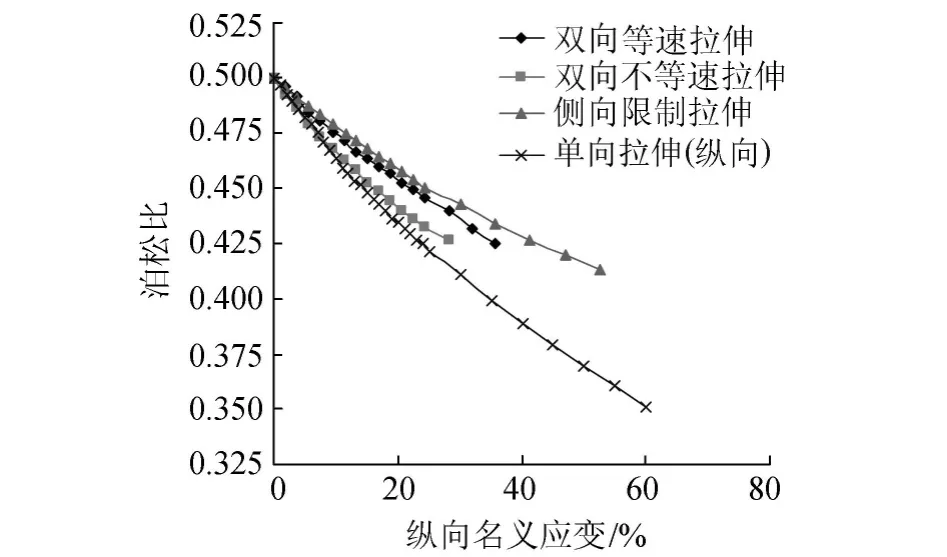
图8 PVC膜单、双向拉伸下泊松比-纵向名义应变关系曲线

3．2．2 HDPE 膜试验结果

图9为HDPE膜在3种双向拉伸条件下的变形状态。由图9可知，在双向拉伸条件下，HDPE膜中心区发生明显的双向拉伸变形，并处于双向不同应力比例的受力状态。同时也可以看出，HDPE膜在纵、横向应变均为24%，纵、横向应变分别为14%和21%，以及纵向应变为30%、横向固定3种状态下试样的4个角点均发生了屈服变形。

图9 典型双向拉伸条件下HDPE膜变形状态

图10为HDPE膜单、双向拉伸真应力随真应变变化曲线。由图10可知，不同拉伸状态下，HDPE膜2个方向上的真应力与真应变在拉伸应变很小的初始阶段均呈良好的线性关系，但之后开始随着应变的增加呈非线性增加，最后进入屈服阶段。单向拉伸状态下HDPE膜纵、横向屈服应变分别为8.614%和8.64%;而3种双向拉伸状态下HDPE膜的屈服应变均不超过5%。双向拉伸状态下的屈服强度较单向拉伸有很大提高，纵向屈服强度最大提高了约97%，横向屈服强度最大提高了22.98%。相对于单向拉伸状态，3种双向拉伸状态下屈服点割线模量也都有显著提高，纵向屈服点割线模量最大提高了274.9%，横向屈服点割线模量最大提高了146.65%。

图10 HDPE膜单、双向拉伸真应力-真应变关系曲线

图11为HDPE膜单、双向拉伸下泊松比随纵向名义应变的变化曲线。由图11可知，单、双向拉伸条件下HDPE膜泊松比均随着纵向名义应变的增大而减小;单、双向拉伸条件下泊松比有一定差异。说明HDPE膜泊松比不仅与应变大小有关系，还与单、双向拉伸状态有关。但单、双向拉伸状态下的泊松比差别很小，在10%应变时，单向与双向拉伸的最大差异只有0.005。

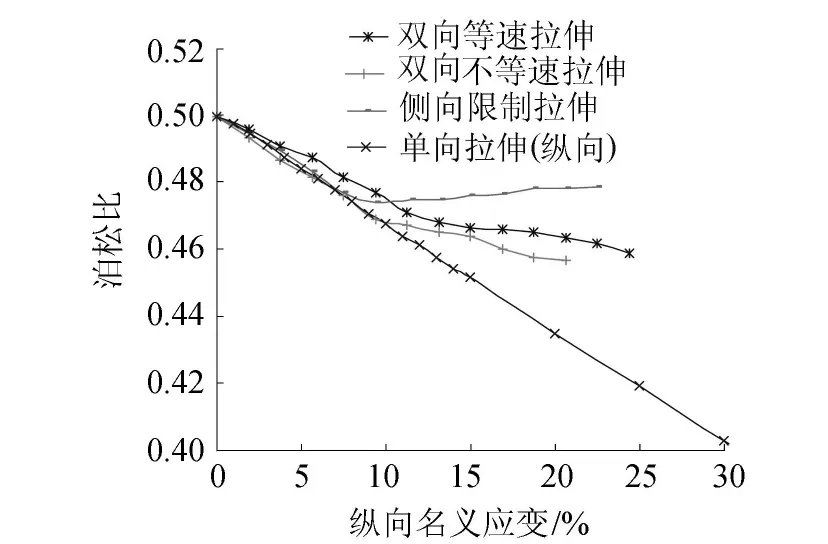
图11 HDPE膜单、双向拉伸下泊松比-纵向名义应变关系曲线

3．3 PE膜“筒”型双向拉伸试验结果

图12为PE膜在不同内压下的双向变形状态。由图12可知，在双向拉伸条件下，试样由圆筒状变为鼓状，PE膜中心区发生明显的双向拉伸变形。同时也可以看出，PE膜在20 kPa、40 kPa和60 kPa这3种内压条件下，轴向应变达到20%时均未发生拉伸破坏。

图12 不同内压下PE膜的变形状态(试样轴向应变为20%)

图13为不同内压下PE膜环向真应力-真应变关系曲线。由图13可知，由于环向应力、环向应变的相对变化范围均较小，因此图中各工况下的环向应力-环向应变关系曲线都比较短，随着环向应变的增大，环向应力尽管存在些许肉眼不可识别的数据波动，但仍呈现明显的线性递增关系。内压越大，环向应力-应变关系曲线在图中的位置越高，反之则越低，且相邻两条曲线之间的应力相对差值大致相等。

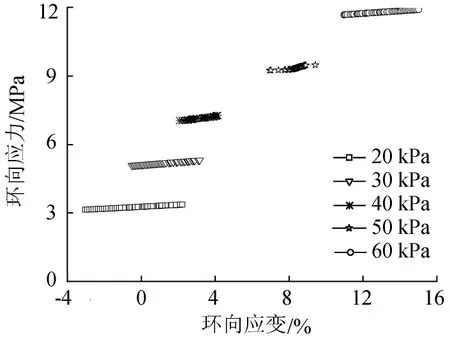
图13 不同内压下PE膜环向真应力-真应变关系曲线

图14为不同内压下PE膜轴向真应力-真应变关系曲线。由图14可知，各工况下轴向真应力-真应变关系曲线呈现明显的非线性关系，轴向应力值伴随着轴向应变值的增大逐渐增大，但增大速率也随之降低，最后进入屈服阶段。PE膜双向拉伸状态下的屈服真应变很小，不同双向拉伸状态下，屈服真应变在5%～7%之间，远低于传统单向拉伸试验结果(10% ～13%);屈服强度随着内压的增大而增大。

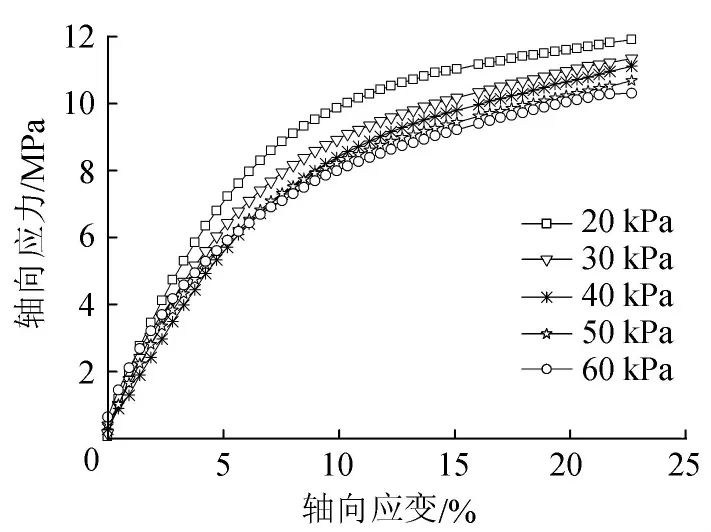
图14 不同内压下PE膜轴向真应力-真应变关系曲线

4 结论

a．采用传统单向拉伸试验方法高估了土工膜的延伸率，将单向拉伸试验结果用于工程设计时是偏于不安全的。双向拉伸试验得到的延伸率、弹性模量等力学特性可以更好地揭示土工膜防渗体运行下的变形特性和破坏机理，因此，应采用双向拉伸试验方法进行高面膜堆石坝防渗膜的力学特性研究。

b．PVC膜具有很强的变形能力，在单、双向拉伸状态下土工膜2个方向上的真应力与真应变均呈近似的线弹性关系，弹性模量与应力状态有关，单向拉伸弹性模量远小于双向拉伸弹性模量;弹性模量还与不同双向拉伸比有关;泊松比随着应变的增大而减小，且减小的幅度也越来越小;单、双向拉伸状态下也有一定差异，但在10%应变以内，不同拉伸状态及不同双向拉伸速率比例的影响可以忽略不计。

c．HDPE膜在双向拉伸状态下的变形能力很有限，双向拉伸真应力与真应变在拉伸应变很小的初始阶段均呈良好的线性关系，但之后真应力开始随着应变的增加呈非线性增加，很快进入屈服阶段，单向拉伸状态下纵、横向屈服真应变分别为8.614%和8.64%，而双向拉伸下的屈服真应变均不超过5%;泊松比也随着应变的增大而减小;单、双向拉伸状态下也有一定差异，但10%应变以内，不同拉伸状态及不同双向拉伸速率的影响也可以忽略不计。

d．PE膜双向拉伸轴向真应力-真应变呈现明显的非线性关系，轴向真应力值伴随着轴向应变值的增大逐渐增大，但增大速率也随之降低。双向拉伸状态下其屈服真应变在5%～7%之间。

e．目前土工膜防渗土石坝数值分析所采用的土工膜本构模型均是基于单向拉伸试验得到的名义应力-名义应变关系，结果与土工膜真实工作状态下的应力-应变性态相差较大。在双向拉伸试验得到的真应力-真应变关系基础上，可建立不同土工膜的双向拉伸本构模型，以应用于高堆石坝面膜防渗体受力变形的数值分析与安全评价中。

［1］束一鸣．防渗土工膜工程特性的探讨［J］．河海大学学报:自然科学版，1993，21(4):1-6．(SHU Yiming．Engineering characters of geomembrane ［J］．Journal of Hohai University:Natural Science，1993，21(4):1-6．(in Chinese))

［2］束一鸣，顾淦臣，向大润，等．长江三峡二期围堰土工膜防渗结构前期研究［J］．河海大学学报:自然科学版，1997，25(5):71-77．(SHU Yiming，GU Ganchen，XIANG Darun，et al．Study on geomembrane for impervious structure of second-stage cofferdam of the three Gorges project［J］．Journal of Hohai University:Natural Science，1997，25(5):71-77．(in Chinese))

［3］高正中，张青云．PVC复合土工膜工程特性试验研究［J］．四川水利，1994，15(5):51-54．(GAO Zhengzhong，ZHANG Qingyun．Experimentalstudyon engineering characteristics of PVC composite geomembrane［J］．Sichuan Water Conservancy，1994，15(5):51-54．(in Chinese))

［4］任大春，张伟，吴昌瑜，等．复合土工膜的试验技术和作用机理［J］．岩土工程学报，1998，20(1):10-13．(REN Dachun，ZHANG Wei，WU Changyu，etal．Testing techniques and functional mechanism of composite geomembranes［J］．ChineseJournal of Geotechnical Engineering，1998，20(1):10-13．(in Chinese))

［5］保华富，胡春风．土工膜的有关物理力学性试验研究［J］．云南水力发电，2004，20(1):13-17．(BAO Huafu，HU Chunfeng．Test and research of relevant physicomechanical properties of geomembrane［J］．Yunnan Water Power，2004，20(1):13-17．(in Chinese))

［6］胡利文，陈嘉鸥．土工膜微结构破损机理分析［J］．岩土力学，2002，23(6):702-705．(HU Liwen，CHEN Jiaou．Analysis of damage for microstructure of geomembrane［J］．Rock and Soil Mechanics，2002，23(6):702-705．(in Chinese))

［7］徐光明，章为民，彭功勋．HDPE膜的力学特性受损伤影响初步研究［J］．河海大学学报:自然科学版，2004，32(1):76-80．(XU Guangming，ZHANG Weimin，PENG Gongxun．Effect of damage on mechanical behavior of HDPE geomembrane［J］．Journal of Hohai University:Natural Sciences，2004，32(1):76-80．(in Chinese))

［8］GIROUD J P．Mathematical model of geomembrane stressstrain curves with a yield peak［J］．Geotextiles and Geomembranes，1994，13(1):1-22．

［9］MERRY S M，BRAY D．Time dependent mechanical responseofHDPE geomembranes［J］．Journalof Geotechnical and Geoenvironmental Engineering，1997，123(1):57-65．

［10］ZHANG C，MOORE I D．Nonlinear mechanical response of highdensity polyethylene(partⅠ):experimental investigation and model evaluation［J］．Polymer Engineering and Science:Ser A，1997，37(2):404-413．

［11］ZHANG C，MOORE I D．Nonlinear mechanical response of high density polyethylene(partⅡ):uniaxial constitutive modeling［J］．Polymer Engineering and Science:Ser B，1997，37(2):414-442．

［12］NIKOLOV S，DOGHRI I．A micro/macro constitutive model for the small-deformation behaviour of polyethylene［J］．Polymer，2000，41(5):1883-1891．

［13］BEIJER J G J，SPOORMAKER J L．Modelling of creep behaviour in injection-moulded HDPE［J］．Polymer，2000，41(14):5443-5449．

［14］WESSELOO J，VISSER A T，RUST E．A mathematical model for the strain-rate dependent stress-strain response of HDPE geomembranes［J］． Geotextiles and Geomembranes，2004，22(4):273-295．

［15］GIROUD J P． Poisson’s ratio of unreinforced geomembranes and nonwoven geotextiles subjected to large strains［J］．Geotextiles and Geomembranes，2004，22(4):297-305．

［16］ASTMD638—10 Standard testmethod fortensile properties of plastic［S］．

［17］ASTMD488—06 Standard test method for determining performance strength of geomembranes by the wide strip tensile method［S］．

［18］BRAY J D，MERRY S M．A comparison of the response of geosynthetics in the multi-axial and uniaxial test devices［J］．Geosynthetics International，1999，6(1):19-40．

［19］ASTMD5617—2004 Standard test method for multi-axial tension test for geosynthetics［S］．

［20］束一鸣，吴海民，林刚，等．土工合成材料双向拉伸蠕变测试仪:中国，201019026078．X［P］．2010-02-05．

［21］吴海民，束一鸣，曹明杰，等．土工合成材料双向拉伸多功能试验机的研制及初步应用［J］．岩土工程学报，2014，36(1):170-175．(WU Haimin，SHU Yiming，CAO Mingjie，et al．Development and application of multifunctional biaxial tensile testing machine for geosynthetics［J］．Chinese Journal of Geotechnical Engineering，2014，36(1):170-175．(in Chinese))

［22］姜晓桢，束一鸣，吴海民，等．土工膜内压薄壁圆筒试样双向拉伸试验装置及试验方法:中国，201210117437.4［P］．2010-04-19．

［23］吴海民．深覆盖层上堆石坝面土工膜防渗结构若干关键问题研究［D］．南京:河海大学，2013．