基于Fisher字典学习的运动想象脑电分类算法*

胥立波，蒋爱民，刘小峰，王 勇

（河海大学物联网工程学院，常州213022）

基于Fisher字典学习的运动想象脑电分类算法*

胥立波，蒋爱民，刘小峰，王 勇

（河海大学物联网工程学院，常州213022）

目前，在以运动想象为基础的脑机接口研究中，共空域模式（Common Spatial Pattern，CSP）算法是脑电信号特征提取的主流算法，而如何利用CSP特征进行有效的分类则是该领域的研究热点之一。近年来，基于稀疏表示的分类方法（Sparse Representation based Classification，SRC）备受国内外学者的高度关注，为此提出了一种基于Fisher字典学习的脑电分类算法。该算法结合了稀疏重构误差和编码系数进行分类。实测数据的处理结果表明，与传统基于SRC的分类算法相比，所提出的算法能够取得更为精确的分类结果。

脑机接口；共空域模式；稀疏表示；Fisher字典学习；重构误差；编码系数

1 引 言

近年来，随着计算机科学、脑科学以及人机交互领域的快速发展，脑机接口（Brain－Computer Interfaces，BCI）技术越来越受到国内外学者的关注，它绕开外周神经和肌肉组织，实现人脑与计算机或其他外部电子设备的直接通信，也就是说仅通过人的大脑思维活动即可与外界交流信息，而不需要通过实际动作［1］。这项技术对于那些有肢体运动障碍的瘫痪病人无疑是一个福音。除了在医疗康复领域，在军事和生活娱乐等方面，BCI也有着独特的应用［2］。

特征提取和分类是脑机接口系统中最主要的两部分。当前，运动想象脑电信号的特征提取主要采用共空域模式（Common Spatial Pattern，CSP）算法［3］；而对于特征分类这一块，也有许多经典算法，如线性判别分析LDA［4］，支持向量机SVM［5］等。

基于稀疏表示的分类技术（Sparse Representation based Classification，SRC）是近年来新兴的信号处理方法，在人脸识别、图像分类等领域［6］得到了广泛应用。对于运动想象脑电信号分类问题，文献［7］直接把脑电信号的训练特征样本作为字典，然后根据l1范数最小化原则［8］求解出表示系数，最后根据求得的系数计算重构误差来确定样本所属的类别。这一分类方法只需要利用高效稀疏编码算法求得表示系数，而无需对字典进行训练，因而计算效率较高。但是，这种方法并不能充分利用各类别间的结构信息，丢失了许多隐藏在训练样本中的分类信息。此外，由于实测数据常常受到噪声感染，直接把训练样本作为字典进行分类会使得求解系数并非如设想的那样稀疏。针对这些问题，提出一种基于Fisher字典学习［9］的方法，通过Fisher鉴别准则［10］从训练样本中学习出一个具有很好判别性能的结构化字典，该字典中各类子字典能够较好地表示该类中的样本，而对于类外样本则具有较弱的表示能力。与此同时，在计算每一个样本特征稀疏表示系数时增加Fisher判别准则项，保证其稀疏表示系数具有较大的类间误差和较小的类内误差，因此在对测试样本进行分类的时候可以综合样本的重构误差值和编码系数两者进行分类。测试结果表明，所提出的分类算法比传统的SRC算法具有更佳的效果。

2 基于稀疏表示的分类方法

传统SRC算法假设同一类的测试样本可以由同类中的训练样本线性表示，因此它将训练样本直接作为字典，然后利用此字典求解稀疏表示系数，最后根据重构误差最小原则进行分类。

文献［7］中，对于给定的两类EEG信号，首先用CSP算法对每个样本进行特征提取，其算法思想是利用代数上矩阵同时对角化的原理，构造出一组空域滤波器，使得滤波后的两类信号一类方差达到极大，另一类方差达到极小，从而达到分类的目的。通过CSP算法提取的特征向量可以表示为：

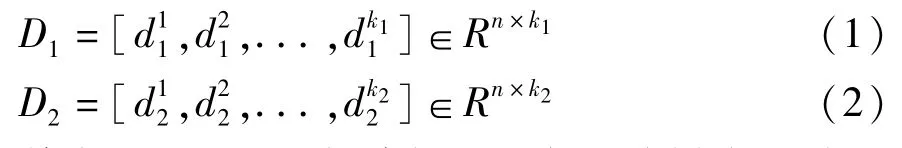
其中，D1和D2分别表示两类训练样本的特征向量集，k1和k2分别表示两类训练样本的个数，n为特征向量的维数。然后把D＝［D1，D2］∈作为字典，D的每一列都是字典的原子。同样用CSP算法提取出一个测试样本的特征向量，表示为y。根据之前的假设，则有：

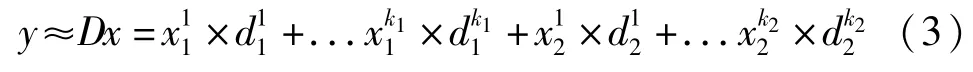
最后，根据式（4）求得的系数计算两类样本信号重构后的误差值，误差值小的那一类就作为样本的类别。公式如下：

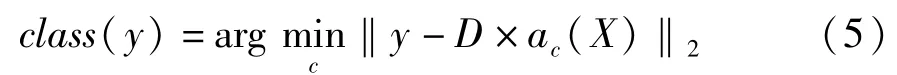
其中，ac（X）函数的功能是选出第c类原子对应的系数，并将另一类的系数置零。从文献［7］中的实验结果可看出，相比于经典的线性判别分析（Linear Discriminant Analysis，LDA），SRC算法在分类精度上有了一定提高。

3 提出方法

3．1 基于Fisher字典学习的分类

基于Fisher判别字典学习的分类算法，是从训练样本中学习出具有更好判别性能的字典，以便获得更佳的分类效果。在原始信号经过预处理后，利用CSP算法提取信号的特征向量，设为A＝［A1，A2，．．．，Ac］，其中c表示样本的类别数。设字典为D＝［D1，D2，．．．，Dc］，对应系数矩阵为X＝［X1，X2，．．．，Xc］，整个字典学习过程可以表示为以下优化问题：

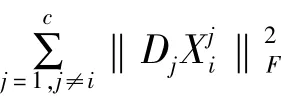
式（6）中，f（X）表示系数矩阵的判别约束项。利用Fisher准则构建此项

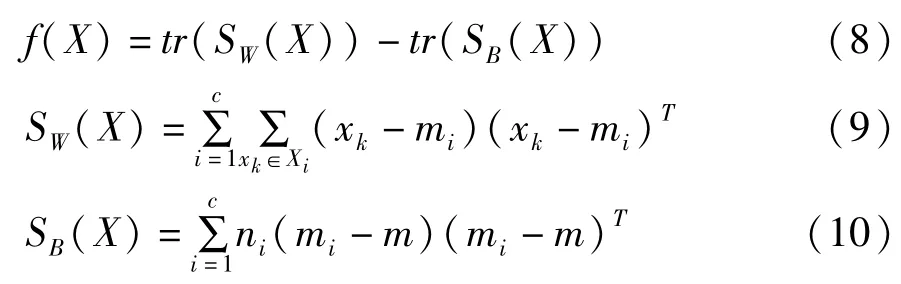
其中，SW（X）表示类内误差，SB（X）表示类间误差，mi和m分别表示稀疏表示系数矩阵Xi和X的均值，ni和n分别表示i类样本和全部样本的数目。

3．2 J（D，X）的最优化

将式（7）和式（11）代入式（6）中，则目标函数最终表示为：

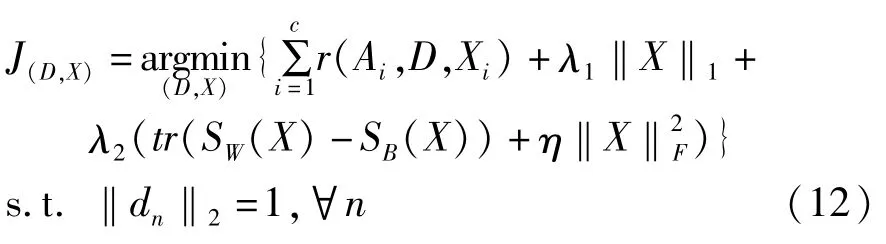
虽然，对于（D，X），式（12）表示一非凸优化问题，但是当固定其中一个时，则可以将其转化为一系列的凸优化问题进行求解。具体步骤如下：

首先，固定D，逐类求解Xi，此时的目标函数可以表示为：

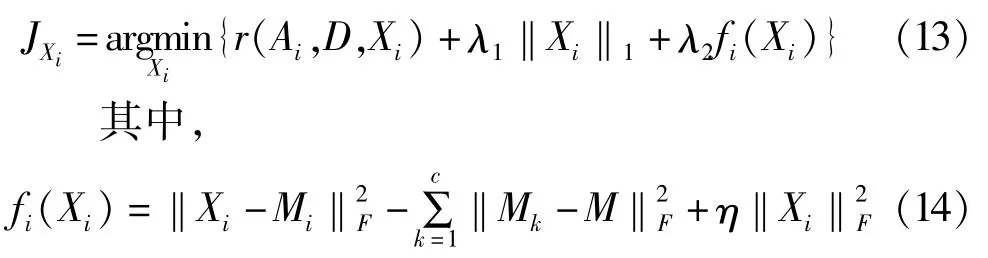
式（14）中，Mk和M表示k类和所有类别的平均系数矩阵。研究表明当η＞1－ni／n时，fi（Xi）为严格凸函数［9］。

把式（13）重新写为：

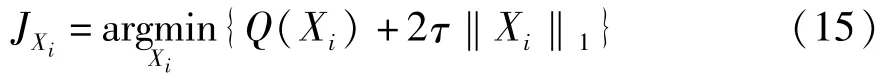
其中，Q（Xi）＝r（A，D，Xi）＋λ2fi（Xi），τ＝λ1／2，定义，xi，k表示矩阵Xi的第k列。由于Q（Xi）严格凸优化于Xi，固式（15）可以通过文献［11］中的迭代投影算法进行求解，具体步骤为：

1．输入：σ，τ＞0。

3．当未达到收敛条件时，令h＝h＋1，

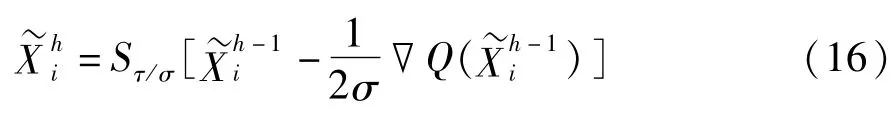
当固定系数X时，逐类更新字典Di。此时的目标函数转化为：

上式是一个二次规划问题，可以通过文献［12］中的算法进行求解，逐步更新字典原子Di。

综上所述，Fisher字典学习法的算法步骤可以总结如下：

Step1把训练特征样本归一化后作为初始字典中的原子。

Step2固定字典矩阵D，通过迭代投影法逐步求解系数矩阵Xi。

Step3固定系数矩阵X，用文献［12］中算法逐步求解字典原子Di。

Step4当相邻迭代中的目标函数值J（D，X）足够逼近，或者迭代次数达到预设值时，输出X和D，否则返回Step2。

3．3 分类方法

利用训练特征样本集，上述Fisher字典学习方法可以获得具有分类特性的字典。当给定测试样本特征y时，求解以下问题，从而获得表示系数：

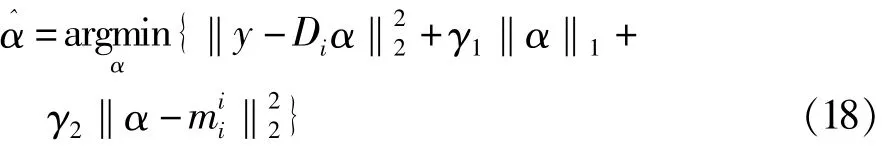
其中，α表示待求的系数向量，γ1和γ2表示加权常量，表示对应字典Di所求得的第子块系数均值。最终的分类则需要计算

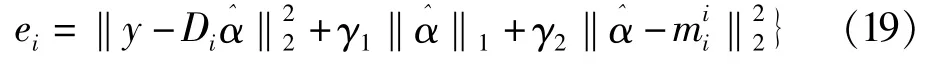
测试样本类别选择使得误差值ei最小的那一类。

4 实验结果分析

实验采用上海交通大学仿脑计算与机器智能研究实验室所公开的运动想象脑电数据（subject1和subject3）进行实验分析（下载地址为http：／／bcmi．sjtu．edu．cn／resource．html）。每组数据集分别有60个训练样本（左右想象运动各30个）和140个测试样本（左右想象运动各70个）。

首先对两类训练样本和测试样本分别提取CSP特征，然后利用所提出的Fisher字典学习方法从训练特征样本中学习出字典，最后再根据分类方法对测试特征样本进行分类。直接根据指定的训练和测试样本进行分类的结果如表1所示。

表1 直接分类的结果

为了进一步提升分类效果，又对两组实验数据进行10次交叉验证计算，实验结果如表2所示。

从表1和表2可以看出，无论是直接按照指定训练和测试样本，还是采用交叉验证的方法，所提出的分类算法性能均优于传统的SRC算法。

表2 交叉验证的分类结果

5 结束语

针对传统SRC方法在字典构造过程中不能充分利用隐藏在样本中的分类信息问题，提出了Fisher字典学习方法。该方法在构建结构化字典方面具有两个优势：第一，每个子字典都有较好的表示对应类别样本的能力；而对于不同类别的样本，每类子字典则具有较大的重构误差。第二，通过该字典求解出的系数矩阵具有较小的类内误差和较大的类间误差。因此在分类时，可综合利用重构误差和表示系数对测试样本进行更为精确的分类。实验结果表明，相比传统的SRC算法，所提出的分类算法具有更高的分类准确率。

［1］ Wolpaw J R，Birbaumer N，Heetderks W J，et al．Braincomputer interface technology：a review of the first international meeting［J］．IEEE transactions on rehabilitation engineering，2000，8（2）：164－173．

［2］ Mak J N，Arbel Y，Minett J W，et al．Optimizing the P300－based brain－computer interface：current status，limitations and future directions［J］．Journal of neural engineering，2011，8（2）：025003．

［3］ Ramoser H，Muller－Gerking J，Pfurtscheller G．Optimal spatial filtering of single trial EEG during imagined hand movement［J］．Rehabilitation Engineering，IEEE Transactions on，2000，8（4）：441－446．

［4］ Muller K，Anderson C W，Birch G E．Linear and nonlinear methods for brain－computer interfaces［J］．Neural Systems and Rehabilitation Engineering，IEEE Transactions on，2003，11（2）：165－169．

［5］ Garrett D，Peterson D A，Anderson C W，et al．Comparison of linear，nonlinear，and feature selection methods for EEG signal classification［J］．Neural Systems and Rehabilitation Engineering，IEEE Transactions on，2003，11（2）：141－144．

［6］ Wright J，Yang A Y，Ganesh A，et al．Robust face recognition via sparse representation［J］．Pattern Analysis and Machine Intelligence，IEEE Transactions on，2009，31（2）：210－227．

［7］ Shin Y，Lee S，Ahn M，et al．Motor imagery based BCI classification via sparse representation of EEG signals［C］．／／Noninvasive Functional Source Imaging of the Brain and Heart＆2011 8th International Conference on Bioelectromagnetism（NFSI＆ICBEM），2011 8th International Symposium on．IEEE，2011．

［8］ Candes E J，Romberg J K，Tao T．Stable signal recovery from incompleteandinaccuratemeasurements［J］．Communications on pure and applied mathematics，2006，59（8）：1207－1223．

［9］ Yang M，Zhang L，Feng X，et al．Sparse representation based Fisher discrimination dictionary learning for image classification［J］．InternationalJournalofComputer Vision，2014，109（3）：209－232．

［10］ Mairal J，Leordeanu M，Bach F，et al．Discriminative sparse image models for class－specific edge detection and image interpretation［M］．Computer Vision－ECCV 2008．Springer Berlin Heidelberg，2008．

［11］ Rosasco L，Verri A，Santoro M，et al．Iterative projection methods for structured sparsity regularization［J］．MIT Technical Report，2009：50－67．

［12］ Yang M，Zhang L，Yang J，et al．Metaface learning for sparse representation based face recognition［C］．／／Image Processing（ICIP），2010 17th IEEE International Conference on．IEEE，2010．

Motor Imagery EEG Classification Algorithm Based on Fisher Dictionary Learning

Xu Libo，Jiang Aimin，Liu Xiaofeng，Wang Yong
（College of Internet of Things Engineering，Hohai University，Changzhou 213022，China）

Now，in the study on motor imagery systems，based on brain－computer interface（BCI），the common spatial pattern（CSP）algorithm is the mainstream algorithm of EEG feature extraction．However，how to use the CSP features to classify effectively is one of the research hotspots in this field．In recent years，the classification method based on sparse representation（SRC）attracts more attention of native scholars and foreign ones．We propose an EEG classification algorithm based on the Fisher dictionary learning which combines the sparse reconstruction error and coding coefficient to classify the signals．The experimental results show that the proposed method can obtain better accuracy rate compared with the traditional classification method SRC．

Brain－computer interface；Common spatial pattern；Sparse representation based classification；Fisher dictionary learning；Reconstruction error；Coding coefficient

10．3969／j．issn．1002－2279．2015．04．014

TP301．6

A

1002－2279（2015）04－0053－04

国家自然科学基金项目（61101158，61471157）；江苏省自然科学基金项目（BK20141159，BK20141157）

胥立波（1991－），男，江苏省盐城市人，硕士研究生，主研方向：生物医学信号处理。

2015－01－26