基于改进Floyd算法的装配供应链网络路径选择研究

江玉杰

（三江学院商学院，江苏 南京 210012）

基于改进Floyd算法的装配供应链网络路径选择研究

江玉杰

（三江学院商学院，江苏 南京 210012）

运用Floyd算法从链上整体效益角度研究装配供应链网络路径选择问题，并综合考虑响应速度、服务质量、物流成本对网络路径选择的影响，引进综合修正因子，以改进传统Floyd算法。结合实例分析结果表明，运用改进Floyd算法选择装配供应链最优网络路径更加贴近现实、更加节省，从而增进链上各节点企业之间的合作程度，最终实现装配供应链稳健高效的运行。

Floyd算法；装配供应链；网络路径选择

0 前言

装配供应链是指以装配制造商为核心，集聚零部件供应商、集配商、分销商、零售商以及配送中心等相关辅助企业，为满足顾客不同需求而形成的供需网络。而装配供应链各节点企业，由于空间距离的限制、各企业的经营特点，需借助运输、配送等物流方式将所需调运的物资按时送达指定的地点，此时所消耗的费用高低、响应速度的快慢、物流质量的优劣必然会影响装配供应链稳定、高效的运行。因此，合理、有效的装配供应链网络路径，能够降低链上各节点企业之间的距离、降低物流成本、提高物流质量，进而提高供应链的柔性，最终实现链上的整体收益大于各自单独运营时所获收益的总和[1]。

目前，专门研究装配供应链网络路径的文献相对较少，文献《基于时间Petri网的供应链网络关键路径分析》[2]采用时间 Petri网研究供应商、生产商、分配中心、零售商、顾客5级供应链网络关键路径；文献《基于VRP模型的两阶段物流网络路径优化模型》[3]基于VRP模型研究供应商、物流中心2级供应链物流网络最优化路径；文献《动态闭环复杂配送网络路径优化算法研究》[4]将正向配送与逆向配送相结合，运用动态规划算法研究闭环配送网络最优化路径；文献《基于复杂网络理论的物流配送路径优化研究》[5]以复杂网络理论为基础，利用动态规划算法研究物流配送最优化路径；文献《供应链弹性综合优化路径选择模型分析》[6]根据木桶理论与效价理论找出供应链中的弹性瓶颈，构造供应链弹性综合优化路径；文献《基于Floyd算法的供应链网络路径研究》[7]以拉动式生产为前提条件，运用Floyd算法研究制造商、配送中心、销售商3级供应链网络路径优化。

上述文献采用不同的理论（时间Petri网、VRP模型、动态规划算法等）对供应链中部分节点企业之间路径进行优化，各有优势，但总体上仅局限于以最低物流成本为指标选择供应链网络路径。鉴于此，本文将以改进Floyd算法研究针对包含响应速度、服务质量、物流成本3项指标的，由供应商、集配商、制造商所组成的装配供应链网络路径选择问题。

1 问题描述

1.1 研究对象

装配供应链中的核心企业即装配制造商，依据TOC理论中关于生产企业分类原则属于A型企业。而A型企业最大的特点是生产过程所需原材料种类很多，甚至有些零部件是最终产品的专用件（即属于卡拉杰克模型中的战略项目）。因而，装配供应链最大的特点是装配制造商的某项需求将驱动上游多家供应商提前通过集配商的运输、配送等物流方式，将所需调运的物资及时、有效的送到指定的地点。基于此，本文研究3个供应商、2个集配商、1个制造商所组成的装配供应链网络路径选择问题。所研究的装配供应链网络路径如图1所示。

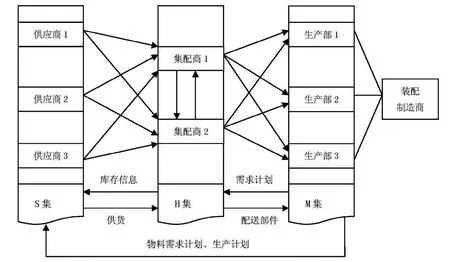
图1 装配供应链网络路径

当5者建立虚拟的动态联盟时，装配制造商（M集）首先根据销售商反馈的销售信息，制定各区域生产计划，利用多级滚动计划向S集（各供应商）、H集（各集配商）发布物料需求计划；其次，各供应商根据制造商发布的生产计划、各集配商反馈的库存信息以及自身生产系统能力大小合理的组织零部件生产；再者，各集配商则会根据各供应商的供货批量大小合理的组织货物的运输，并对其进行集中管理，同时依据制造商的物料需求计划将零部件配送至各生产部；当遇到特殊情况时，并征求供应商、制造商都同意的前提下，集配商之间可以相互调拨物资以满足装配制造商的需求[1]。在此运作模式下，装配供应链便形成复杂交错的网络路径。

1.2 假设前提

在现实社会中，装配供应链各节点企业通常处于多条供应链中，为了便于研究装配供应链网络路径选择问题，本文做出如下假设：

1）装配供应链各节点企业能实现信息完全共享且链条运作正常。

2）S集中的各供应商的供货能力相同且无明显限制，并通过H集中的集配商统一供货给制造商各区域生产部。

3)在紧急情况下（如供应商突发停产、自然灾害以及其他不可抗力情况等），并获得其他供应商以及制造商同意的情况下，集配商之间可以相互调拨物资。

4）装配供应链最优网络路径选择以综合指标值最小为衡量标准。

2 建立数学模型

2.1 基于传统Floyd算法的网络路径选择

Floyd算法，又称弗洛伊登算法、插点法，是一种用于寻找给定的加权网络图中任意2个顶点之间最短路径的算法，边权可正可负[8]。

2.1.1 符号描述

本文所研究的装配供应链中涉及8个节点，根据Floyd算法原理可设：

1）供应商1~3分别为v1、v2、v3，集配商1~2分别为v4、v5，装配制造商中的生产部1~3分别为v6、v7、v8，则装配供应链网络路径中顶点的集合可表示为：V=｛v1,v2,v3,v4,v5,v6,v7,v8｝；

2）（vi,vj）表示一条从顶点vi（i=1,2,…,8）指向vj（j=1,2,…,8）的弧，则装配供应链网络路径中弧的集合可表示为：A=｛（vi,vj）｝。

3）装配供应链网络路径的权矩阵：D=（dij）8x8。

其中，d=lij表示：顶点vi到vj有直接相通的弧时，通过此路时所花费的费用；dij=∞表示；顶点顶点vi到vj没有直接相通的弧时，无法通过此路，即想要通过此路时将花费无穷大的费用。进而简化的装配供应链网络路径如图2所示。

2.1.2 算法步骤[8]

1）根据装配供应链网络各弧路权值（即通过此路所花费的费用），可写出初始权矩阵D（0）=D。

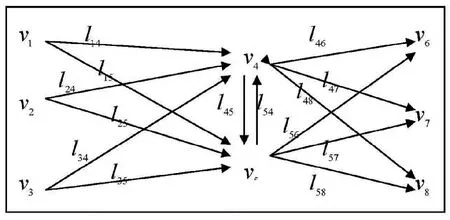
图2 简化的装配供应链网络路径

2）依次计算D（k）=（）8×8，其中d=min（k=1,2,…,8）。而（dij）（k）表示从顶点vi到vj取其直接有弧或借v1、v2、…vk、点为中间点时的最小费用中的最小值[8]。

3）迭代到第8次即可得到装配供应链网络路径的最优解，此时任意两点间的最小费用为：D（8）=（）8×8。值得注意的是在每次迭代时可保留下标信息，既可给出每次迭代后任意两点间的最小费用，也可给出具体路径的最低费用。

2.2 基于改进Floyd算法的网络路径优化

运用传统 Floyd算法选择网络路径只是基于最低物流成本指标，并没有考虑因路径的长短导致装配供应链的响应速度、物流质量的差异。在现实社会中，任意两点间的路长与通过此路所花费的费用并不成正比。倘若仅以最低物流成本为指标选择网络路径，可能因路长相对过远而使供应商供货提前期拉长、集配商物流服务质量下降、制造商因缺短货而停工待产，致使影响装配供应链的稳定性[6]。

为此，本文综合考虑装配供应链的响应速度、物流质量的影响，引入通过vi到vj路物流费用的综合修正因子ij，并以lij+ij作为新的路权值。然后重新运用传统的Floyd算法求解，即通过8次迭代后便可求出装配供应链网络路径的最优解。值得注意的是通过路径仿真技术、先验数据挖掘技术等，可以在既定的置信区间内估计求得综合修正因子ij值。

3 实例分析

C.M汽车装配集团成立于1980年6月，座落在风景秀丽的深圳。受到今年4、5月份汽车供销量的下滑，加之原先部分零部件供应商终止供货，公司高层需要重新规划零部件进货渠道。经过几月磋商，已建立新的装配供应链网络路径。目前，该公司的生产部1、2、3需进一批零部件，可选进货路线如图3所示。其中，各节点之间的物流费用为每条弧上的权值，单位为万元；v1、v2、v3分别表示供应商A、B、C；v4、v5分别表示集配商1、2；v6、v7、v8分别表示C.M汽车装配集团的生产部1、2、3。

3.1 背景资料

1）供应商A、B、C向C.M汽车装配集团的生产部1、2、3供应相同的零部件，即克莱斯勒发动机、采埃孚自动变速箱、普莱德电池，且产品性价比相当。

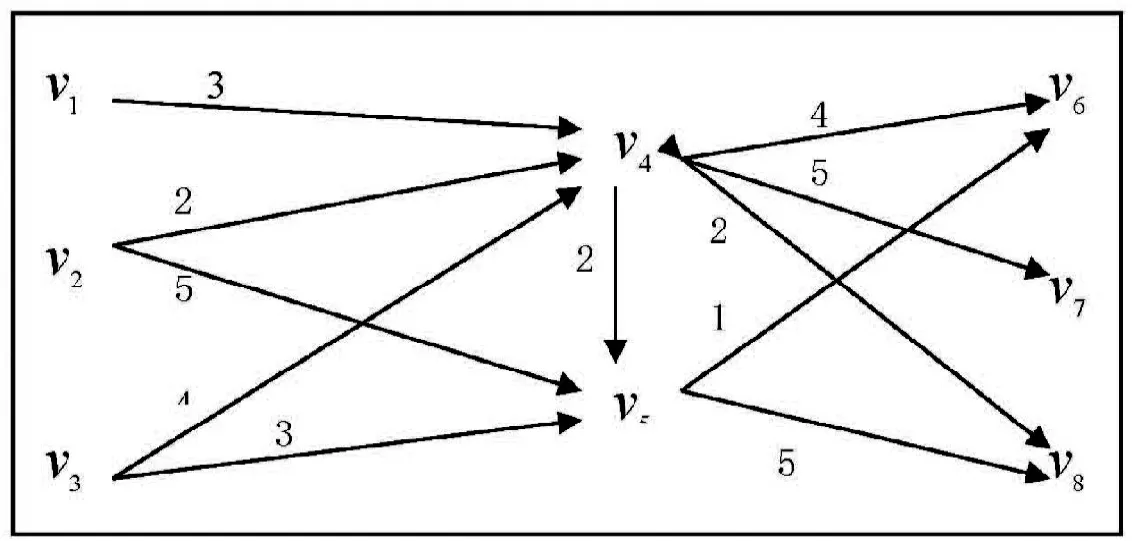
图3 装配供应链赋权网络路径

2）根据公司高层之间的磋商，集配商2可向集配商1调货，但集配商1不可以向集配商2调货，并约定供应商向 C.M汽车装配集团生产部供货需事先将零部件提前转运到集配商1、2处进行统一管理，以便实现共同配送。

3）由于供应商A所处地理位置因素，只能将零部件转运到集配商1处。4）因生产部2的生产规模相对较小，只需由集配商1负责配送零部件。

3.2 运用传统Floyd算法的网络路径选择

1）基于传统Floyd算法步骤，结合图3数据，易得初始权矩阵。

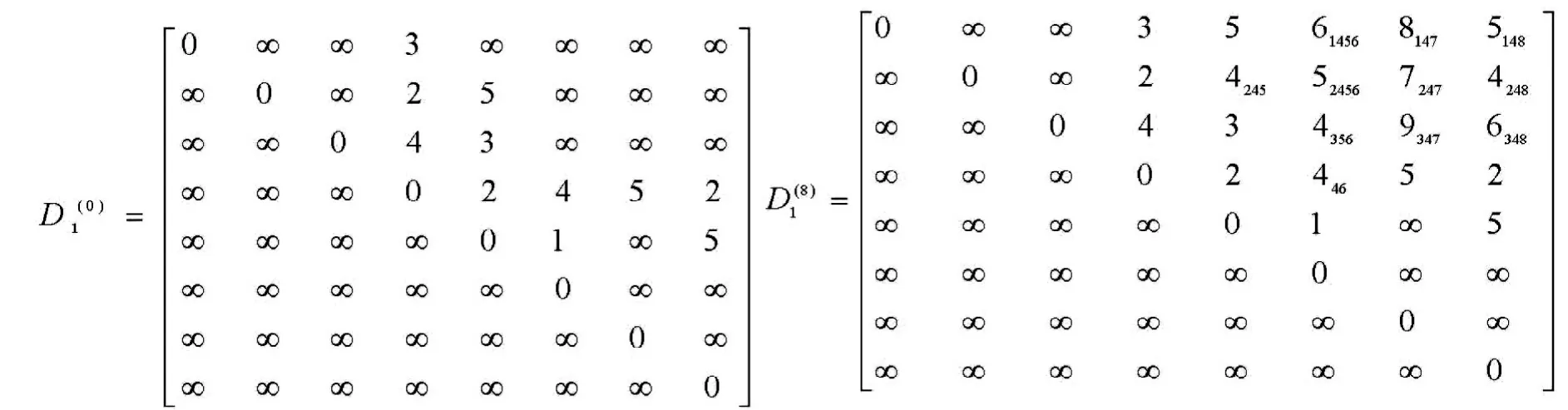
3.3 运用改进Floyd算法的网络路径优化

通过路径仿真技术、先验数据挖掘技术，结合C.M汽车装配集团生产部进货路线的特点，易知通过vi到vj路物流费用的综合修正因子ij，并用lij+ij作为新的路权值，其变化情况如图4所示。

1）基于传统Floyd算法步骤，结合图4数据，易得改进后的初始权矩阵。

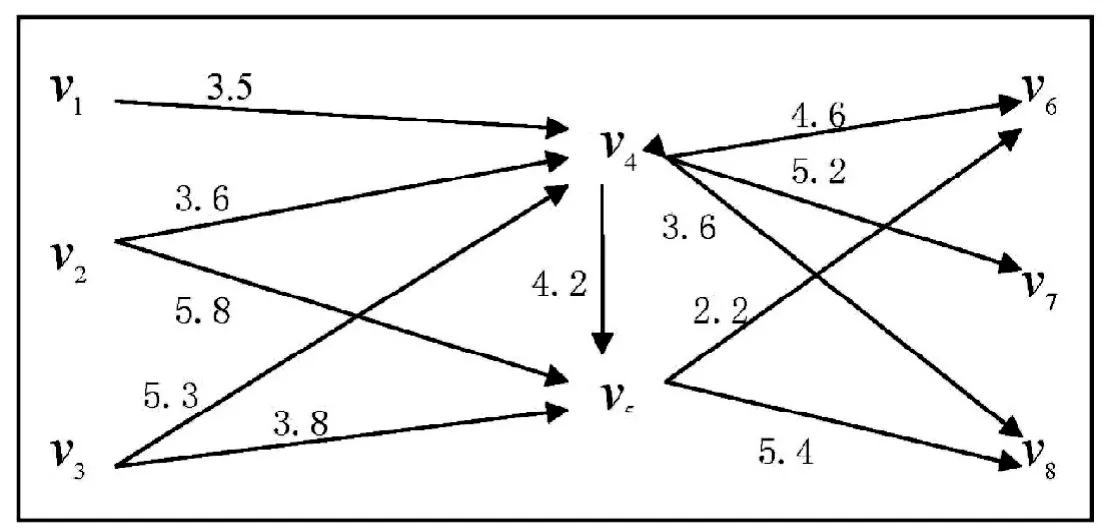
图4 改进后的装配供应链赋权网络路径

3.4 两种路径选择的比较

把基于传统Floyd算法的进货分配方案与基于改进Floyd算法的的进货分配方案进行比较，可以看出：1）运用改进Floyd算法进行装配供应链网络路径选择时，可以避免出现两种或多种方案都符合筛选条件，以致影响领导层的决策力；2）运用改进Floyd算法所得进货方案是运用传统Floyd算法所得进货方案的子集，这样可以缩小备选方案的数量，降低决策失误的可能性；3）经过对vi到vj路物流费用的修正，所得综合指标值更能体现现实情况。因此，改进后的进货方案更有助于供应商、集配商以及装配制造商之间的合作，从而间接地提高装配供应链稳定高效的运行，最终实现整体收益大于各自单独运营时所获收益的总和。

4 结语

从供应链整体效益角度研究供应商、集配商和制造商所构成的装配供应链最优网络路径选择问题。综合考虑三维虚拟动态联盟网络路径选择的影响因素，对传统 Floyd算法进行改进，采用兼顾供货提前期、物流质量以及物流成本的网络路径优化方案。实例分析表明，改进的 Floyd算法选择最优网络路径更加贴近现实，从而保证装配供应链稳健牢固运行。

总体而言，运用改进的 Floyd算法选择最优网络路径，对装配供应链的进一步研究具有一定的指导意义，对汽车、造船等企业具有一定的现实应用价值。但不可否认，对到路的物流费用的综合修正因子的确定需进一步的研究。

[1]江玉杰.基于改进Shapley值法的装配供应链收益分配研究[J].山东交通学院学报，2015(01)：36-40.

[2]刘振峰,陈燕.基于时间Petri网的供应链网络关键路径分析[J].数学的实践与认识，2006(11)：32-37.

[3]陈岱莲,李鹏.基于VRP模型的两阶段物流网络路径优化模型[J].重庆交通大学学报(自然科学版)，2009(06)：1131-1134.

[4]张旭凤,张永安,杨丽.动态闭环复杂配送网络路径优化算法研究[J].中国流通经济，2010(04)：34-37.

[5]曾云,刘宗武.基于复杂网络理论的物流配送路径优化研究[J].物流技术，2011(17)：113-114.

[6]刘家国,周粤湘,李俊,等.供应链弹性综合优化路径选择模型分析[J].哈尔滨工业大学学报，2014(05)：101-106.

[7]楼振凯.基于Floyd算法的供应链网络路径研究[J].物流工程与管理，2014(05)：127-128.

[8]胡运权.运筹学教程（第二版）[M].北京:清华大学出版社,2003:226-228.

Research of Network Path Selection of Assembly Supply Chain Based on Floyd Algorithm Improvement

JIANG Yu-jie
(School of Business,Sanjiang University,Nanjing 210012,China)

This paper studies the network path selection of assembly supply chain from the overall efficiency on the chain by using Floyd algorithm.By taking the effect of the response speed,service quality and logistics costonnetworkpathintoconsideration,comprehensivecorrectionfactorshavebeenintroducedsoastoimprove the traditional Floyd algorithm.Based on the example analysis,the result shows that it is closer to reality and moreeconomicalto use theimprovedFloyd algorithmto choosetheoptimalnetwork path,which mayenhance the cooperation between each node in the chain of enterprises and finally realize the stable and efficient operation of assembly supply chain.

Floyd algorithm;assembly supply chain;network path selection

TP301.6

A

1674-2346(2015)04-0067-06

(责任编辑：田 犇)

10.3969/j.issn.1674-2346.2015.04.014

2015－08－23

江玉杰，男。研究方向：供应链管理