欧式期权市场中带消费行为的投资策略研究

郑兆顺 , 孙述雷

(1.濮阳职业技术学院，河南 濮阳 457000；2.濮阳市第七中学,河南 濮阳 457000)



欧式期权市场中带消费行为的投资策略研究

郑兆顺1, 孙述雷2

(1.濮阳职业技术学院，河南 濮阳 457000；2.濮阳市第七中学,河南 濮阳 457000)

摘要：以随机微分方程理论为依托,在经典Black-Scholes模型的基础上进行补充,对欧式期权市场中的投资策略进行了研究,给出了满足预算条件的消费行为的参数限定.

关键词：Black-Scholes模型;欧式期权;消费行为;投资策略

0引言

在欧式期权的研究领域中,Black-Scholes模型[1]是被广泛应用的基础模型,国内外学者不断对其进行补充修正以适应真实市场,派生出了一些子模型.有些在参数和随机过程上改进,比如将波动率等固定参数改进为关于时间的变量[2],添加了跳过程[3];有些则细化了限定条件以便于更精确地刻画某一具体类型的期权,解决其定价和对冲的问题,比如外汇交易期权模型[4],支付离散红利的交换期权模型[5]等.

上述模型都有一个共同的假设,那就是在欧式期权到期日之前期权持有人不存在消费行为，但这并不符合真实的市场情况.本文将解除这一限定,将消费行为引入到Black-Scholes模型中,并且给出使得期权持有人不超出预算的消费行为需满足的条件.

1模型

下面给出消费行为预算可行的定义.

(1)

2)∀t∈[0,T]，

(2)

3)∀t∈[0,T],c(t)≥0；

4)∀t∈[0,T],随机变量

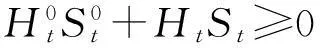
(3)

(4)

那么称(c(t))0≤t≤T是初始资产为x的预算可行消费行为.

现有一投资者,初始资产为x,打算在St高出K时,单位时间消耗相当于ρ份风险资产的财富.用数学语言表达就是c(t)=ρStχ{St>K}.要探讨的问题是：要使消费行为预算可行,ρ和K需要满足什么样的条件.

定理1如果(c(t))0≤t≤T是一个非负值的适应过程,那么它是初始资产为x的预算可行消费行为当且仅当

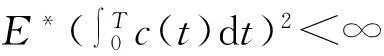
(5)

并且

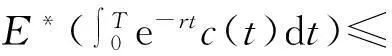
(6)

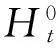
所以

(7)

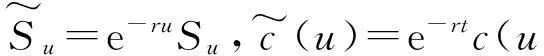
(8)

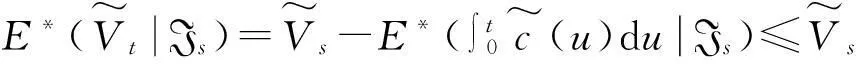
(9)

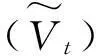
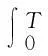
(10)

因此

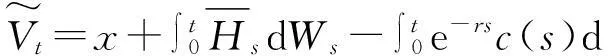
(11)

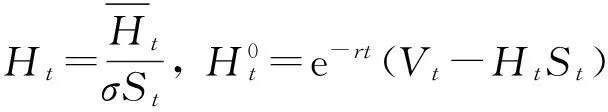
(12)

也就是说

(13)

(14)

所以

(15)

即

(16)

所以条件2)得到满足，其他3个条件经过验证也得到满足,并且V0=H0S0=x.

(17)

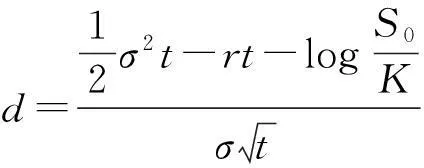
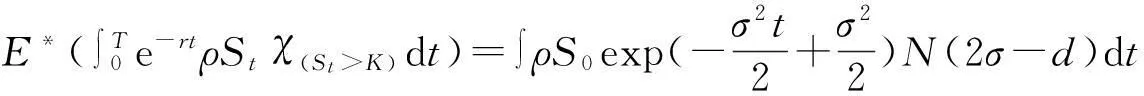
(18)

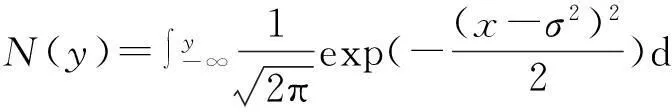
使该消费行为预算可行的ρ和K要满足的条件是

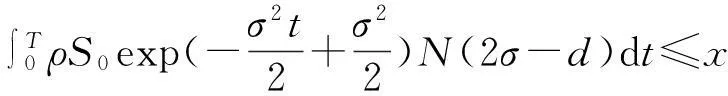
(19)

其中参数K被包含在d中.

2总结

本文在Black-Scholes基本模型的基础上,引入了消费行为——初始资产为x,打算在St高出K时,单位时间消耗相当于ρ份风险资产的财富.通过改进的新模型,找到了保持预算可行状态的消费行为需要满足的条件,也就是参数ρ和K要满足的数学表达式.这就为资产持有人提供了制定消费策略的依据与限制.

参考文献

[1]BLACK F, SCHOLES M. The pricing of options and corporate liabilities[J]. Journal of Political Economy, 1973,81(3):637-654.

[2]任智格,何朗,黄樟灿.一种无风险利率时变条件下的Black-Scholes期权定价模型[J].数学杂志,2015,35(1):203-206.

[3]朱霞,葛翔宇.股票价格服从指数O-U跳扩散过程的期权定价[J].统计与决策，2015(399):164-166.

[4]郑兆顺.外汇后市期权定价与对冲[J].濮阳职业技术学院学报, 2014,27(6):133-135.

[5]全志勇,王瑜.支付离散红利的交换期权定价[J].经济数学, 2010,27(1):26-29.

A Study on Strategies with Consumption in European Options Market

ZHENG Zhao-shun1, SUN Shu-lei2

(1.PuyangVocationalandTechnicalCollege,Puyang457000,China;

2.No.7MiddleSchoolofPuyangCity,Puyang457000,China)

Abstract:Using the theory of stochastic differential equations, the classic Black-Sholes model is improved. The investment strategies with consumption in European options market are discussed and the conditions under which the consumption is budget-feasible are presented.

Key words:Black-Sholes model; European options; consumption; investment strategies

中图分类号：F224.7

文献标识码：A

文章编号：1007-0834(2015)02-0046-03

doi：10.3969/j.issn.1007-0834.2015.02.013

作者简介：郑兆顺(1964—)，男，河南濮阳人，濮阳职业技术学院教授，主要研究方向：数学建模.

收稿日期：2015-03-17