塔康脉冲峰值滑动窗检测与方位包络拟合方法

曾定坤，张 斌，姜力茹，张 博

(空军工程大学信息与导航学院，陕西西安710077)

0 引言

塔康(tactical air navigation，TACAN)作为一种近程无线电导航系统，是现阶段航空最主要的导航设备之一［1-2］，主要为航空目标提供方位与斜距信息，实现极坐标定位［3］。现用的塔康系统由地面信标与机载设备组成，以模拟体制为主［4］，但由于模拟体制存在难与数字设备通信、定位精度不高、噪声容忍度低等缺陷，中频数字化技术逐渐在塔康系统中得到应用［5］。

基于塔康数字化，文献［6］采用相关接收法进行峰值检测，能在一定程度上消除高斯白噪声，但在接收脉冲幅值未知，信噪比较低时，误差较大。文献［7］的匹配滤波峰值检测法利用塔康特定信号格式来获得高精度数据，可是当信号受到多径干扰、大噪声等因素影响而使脉冲形变时，精度将急剧下降。

本文从时域出发，设计与钟形脉冲相匹配的窗函数，在滑动窗函数的同时，比较窗内各离散点与首尾点的幅值来判定峰值到达时刻，累加离散点做归一化估计峰值大小。该方法能有效抑制脉冲宽度变化引起的误差，同时最大限度地抵消信号中存在的高斯白噪声。对获得的峰值点进行包络拟合［8］，采用二次迭代的最小二乘方法，即以一定比例剔除周期内不服从包络分布趋势的峰值点，并重新拟合来提高方位测量精度，二次迭代可抑制噪声与严重偏差包络分布点的影响［9］。

1 塔康信号数学描述

塔康机载设备接收到的信号可表示为

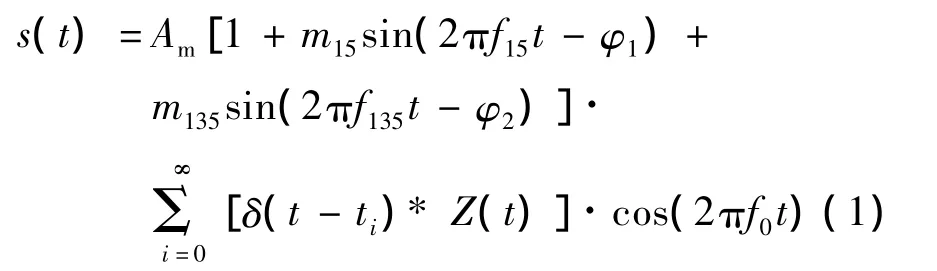
(1)式中:Am为载波信号幅值;m15(m135)为15 Hz(135 Hz)正弦包络信号调制度;f15=15 Hz;f135=135 Hz;φ1(φ2)为15 Hz(135)Hz正弦包络信号初相;δ(t－ti)为编码器输出脉冲列的任一脉冲，有一定宽度;ti为脉冲到达时刻;*表示相关符号;f0为载波频率;Z(t)为钟形脉冲对，包括主基准脉冲群、辅基准脉冲群、询问回答脉冲对和随机填充脉冲对，其表达式为

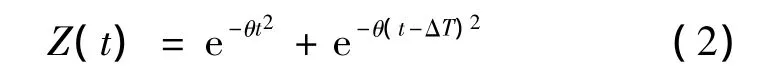
机载设备采用中频数字化技术，处理后的数字中频信号经下变频和采样可得离散化的视频信号，表达式为

(3)式中:T=1/fs，其中，fs为系统采样率。

数字化的塔康系统以主基准脉冲群的第10对脉冲到达时间作为周期起点，周期内约3 000对脉冲［10］。检测出周期内峰值点后，利用最小二乘拟合包络，φ1，φ2的值便可确定，由于周期时间起点就是主基准脉冲的到达时刻，方位数据可由(4)式确定

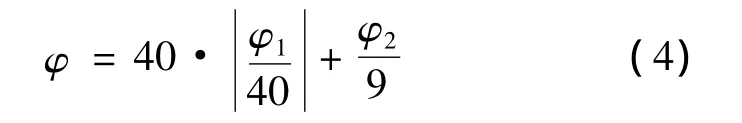
2 峰值检测与估计

峰值检测可以有效检测脉冲峰值与到达时刻。现用塔康系统采用半幅探测电路进行峰值检测，但受幅度变化、参考电压、延迟线路和噪声等因素的影响较大［11-12］。数字化的塔康系统中，匹配滤波器法及滑动窗函数法则是较好的选择。

2.1 匹配滤波器法

匹配滤波器是一种最佳线性滤波器，能使输出信噪比在某一特定时刻达到最大。在塔康系统中，设计与已知脉冲信号匹配的滤波器，当脉冲信号通过滤波器后会出现相关峰。滤波器能在较低的信噪比环境中检测脉冲，但是对脉冲宽度的变化非常敏感，很难准确估计峰值点幅值。

ti时刻进入匹配滤波器的脉冲信号表示为

(5)式中，Pti为ti和ti+ΔT时刻的包络幅值，由于ΔT=12 μs非常小，可认为幅值基本不变。将(2)式代入(5)式后可得

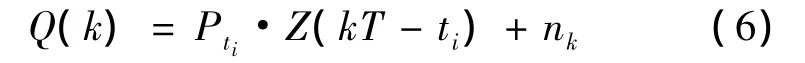
根据匹配滤波器求解脉冲响应的步骤可得到输入信号为Q(k)时的响应函数为

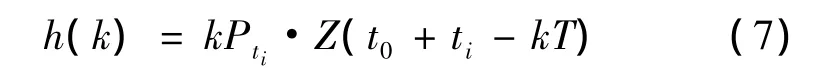
鉴于匹配滤波器对信号的幅值和相位具有适应性，右移时间t0=6 μs，可简化(7)式为

塔康信号进入响应函数为h(k)的匹配滤波器后会在某一时刻出现相关峰，表明脉冲到达，进而获得所需数据。

2.2 滑动窗函数法

塔康脉冲信号在半幅度时的宽度只有3.6 μs，脉冲占空比大，多数时间只有底部的抖动噪声。在脉冲信号中加上一个长度为1.8 μs的滑动窗函数，当用10 MHz的频率进行采样时，窗函数会以18个采样点的长度随时间在脉冲信号上进行滑动。检测窗函数中间16个采样点幅值，如果存在大于首尾2点的情况，则预判有脉冲到达，滑动一位继续对窗内的采样点进行检测，同时设置参数T且初始化为0，检测成功一次，T加1。理想情况下，当T超过门限值M且窗函数中间16个采样点的幅值全部大于首尾2点时，宣布脉冲到达，记录到达时刻。M在无噪声情况下设为8，有噪声时可略低。滑动窗函数算法的具体流程如图1所示。

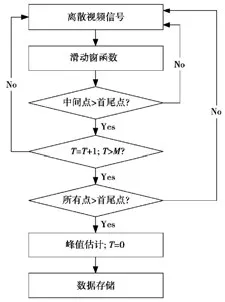
图1 滑动窗函数方法流程Fig.1 Sliding window function flow chart

滑动窗函数法拓展了判定过程中使用到的采样点，累加后能非常有效地抑制噪声对峰值检测的影响，从而更加准确地估计峰值和脉冲到达时刻。此外，滑动窗函数法对脉冲宽度的变化不敏感，能更好地保留脉冲信号中的复杂频率成分，且硬件实现非常简单，只需一系列并排延迟寄存器和相应的数据处理模块、存储模块便可实现。

2.3 峰值估计

检测成功后，峰值和脉冲到达时刻值就可确定，如果直接把到达时刻对应的脉冲幅值作为峰值，受噪声的影响会非常大。基于窗函数算法，可以非常方便地实现以峰值点为中心向两边逐渐降低权值求幅值的方法。

预判有脉冲到达时记为ti，此时窗中各采样点可表示为

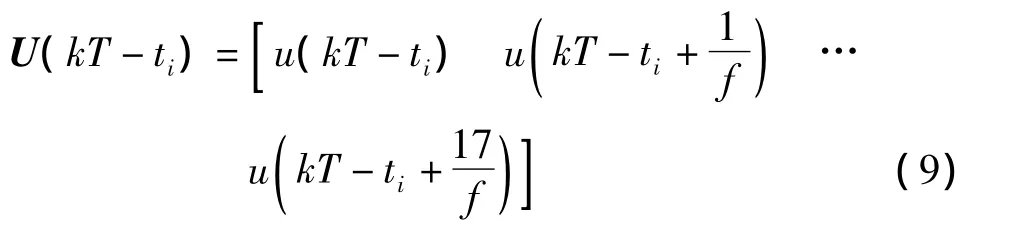
(9)式中:f为采样频率;u(kT－ti)为ti时刻脉冲幅值与噪声的叠加，表示为

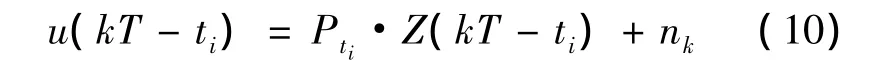
从ti开始经过16个时刻点的滑动，窗内便不会再出现中间采样点幅值超过首尾点的情况，记为

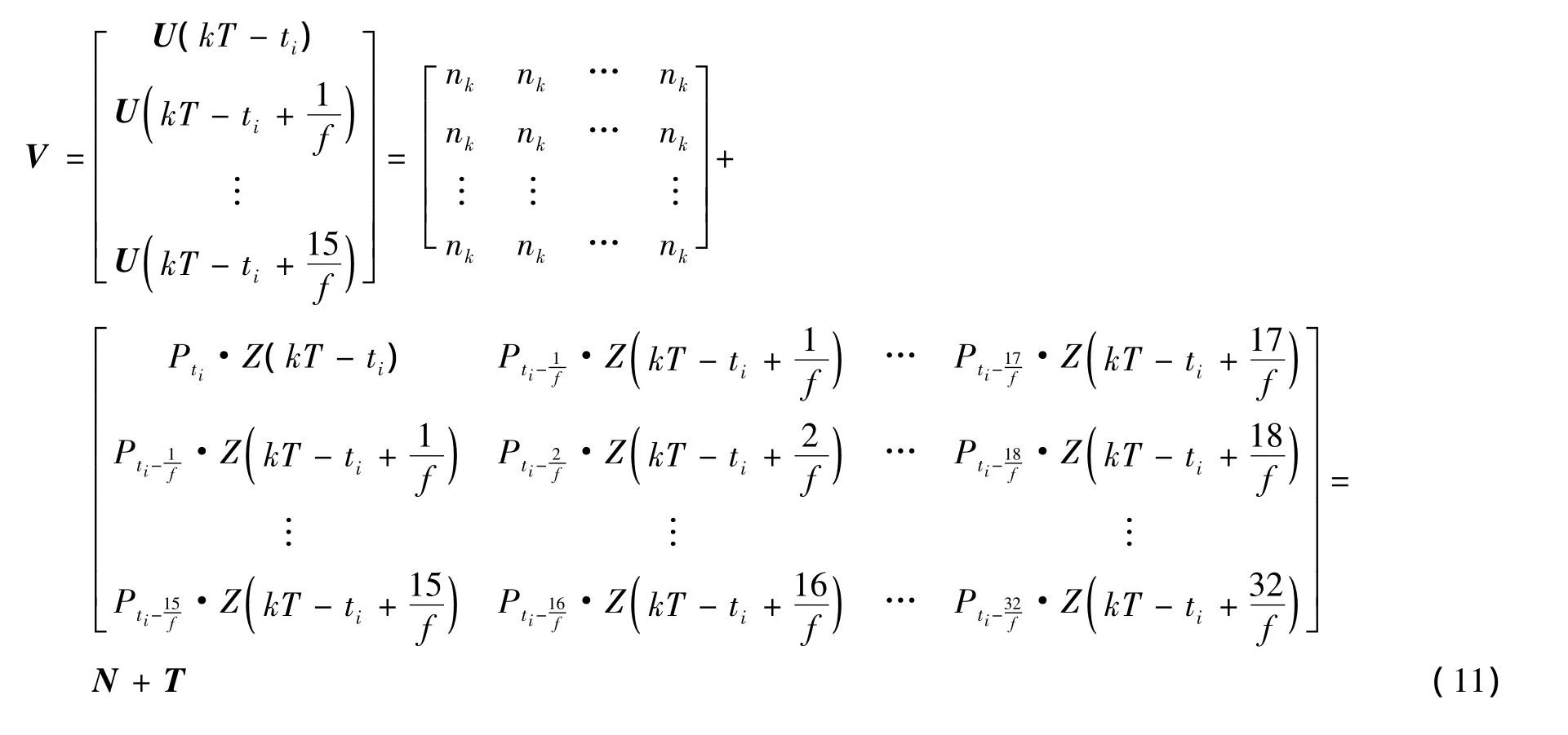
(11)式中:T为采样点的幅值;N为采样点附带的随机高斯白噪声。

(11)式为滑动窗函数在峰值检测过程中所能提供的所有有效采样点，V的每一行对应窗内某个时刻的采样数据。矩阵T中与反对称线平行的采样点幅值相等，因此，只需对T中所有数据进行一次累加便能实现以峰值为中心向两边逐渐降低权值求幅值。累加公式表示为

3 方位估计

现用塔康系统采用比较基准脉冲群与包络正斜率过零点估计方位，但正斜率过零点的选取受噪声影响严重。数字化系统中，考虑到峰值点的间隔比较大，用最小二乘法拟合峰值点获得包络并估计方位［8］。

3.1 数据处理

对峰值点进行最小二乘拟合时，少数不符合包络分布的点可能会对方位估计造成较大误差［10］。本文采用二次迭代的方法滤除这些点，具体做法是以一定比例剔除不符合包络分布的点并重新拟合来提高方位估计精度，包络拟合流程如图2所示。

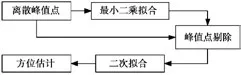
图2 包络拟合流程Fig.2 Envelope fitting flow chart

对峰值点进行最小二乘拟合可得到未处理的包络G，峰值点在对应时刻与G进行比较可获得残差数组F，F越小，表示峰值点与第一次拟合的包络越接近。把F中的数据由大到小降序进行排列得到数组，以一定比例剔除中最大数据对应的峰值点进行二次拟合。

3.2 最小二乘拟合

离散化的视频信号如(3)式所示，其中，第i个峰值点可写为

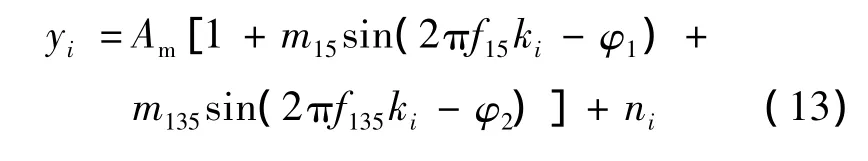
(13)式中:ki为第i个峰值点的位置;ni为噪声。

(13)式中只有Am，m15，m135，φ1，φ2这5个未知参数，定义拟合系数cj(j=1，2，…，5)以及相互独立的函数1，sin(2πf1ki)，cos(2πf1ki)，sin(2πf2ki)，cos(2πf2ki)，便可直接拟合出信号，其中，1用来拟合直流分量，f1，f2根据需要确定。建立目标公式

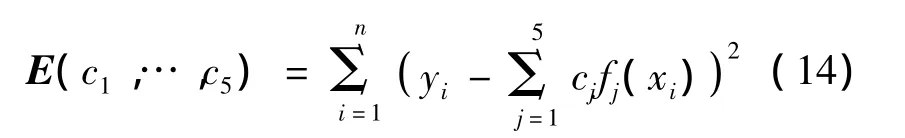
(14)式中，n为每次拟合的峰值点数。

为使误差平方和最小，对(14)式求cj(j=1，2，…，5)的偏导且令全为零。得到关于cj(j=1，2，…，5)的线性方程组为

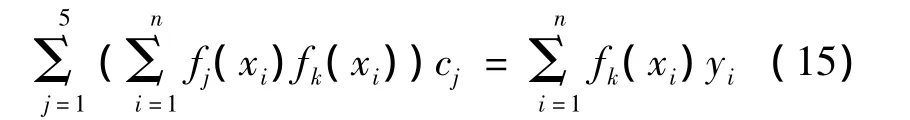
求得拟合系数cj(j=1，2，…，5)后可由象限关系和反正切关系得到φ1，φ2，具体求解方法可参考文献［13］。

4 算法性能验证

采用MATLAB进行仿真验证，在不同信噪比情况下对本文所提方法与其他方法进行了比较分析。塔康信号参数设置如表1所示。

表1 塔康信号参数设置Tab.1 TACAN signal parameter settings

在不同信噪比条件下，分别用匹配滤波器法与滑动窗函数法对同一脉冲进行多次峰值检测，观察检测到的峰值变化，结果如图3所示。

可见，在0 dB功率信噪比情况下，滑动窗函数法进行峰值估计时幅度抖动明显比匹配滤波器小，随着信噪比提高，2种方法测得的幅度逐渐趋于平稳，抖动概率变小。增加验证次数，对获得的数据进行统计分析，分别计算在0，10，20 dB信噪比时，2种方法的峰值与真实幅值之间的误差均值与误差标准差，结果如表2所示。

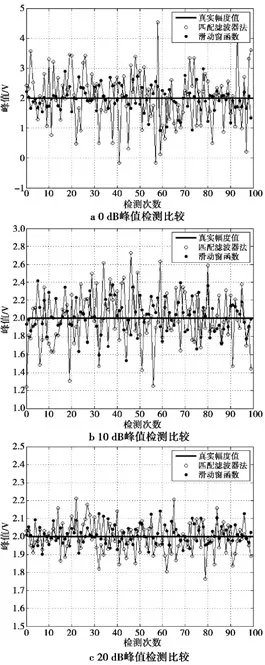
图3 0，10，20 dB时，2种检测方法峰值点幅值比较Fig.3 Comparison of points from diverse detection method when 0，10，20 dB

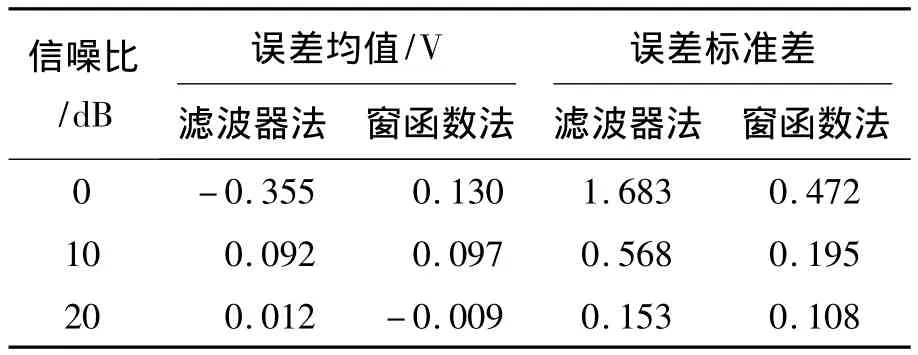
表2 不同信噪比下2种峰值检测方法的误差数据分析Tab.2 Data analysis of two methods under different SNRs

由表2可以看出，在20 dB功率信噪比时，匹配滤波器法的误差均值和误差标准差与窗函数法相差不大，随着信噪比的降低，匹配滤波器法的误差标准差迅速变大，而窗函数法虽然有所提高，但整体上还算平稳。观察误差均值变化情况，在10 dB时，2种方法相差不大，而0 dB时，滤波器法略有提高。因此，2种算法对峰值的计算精度相当，但是滑动窗函数法稳健性远高于匹配滤波器法。

为了进一步比较算法性能，在10 dB功率信噪比情况下，对一个周期的视频信号分别采用匹配滤波器法和滑动窗函数法进行峰值检测，每种方法随机选取100个峰值点(如图4所示)。由图4可看出，匹配滤波器法有少数峰值点会偏离信号包络，而滑动窗函数法服从包络分布趋势且较稳定。

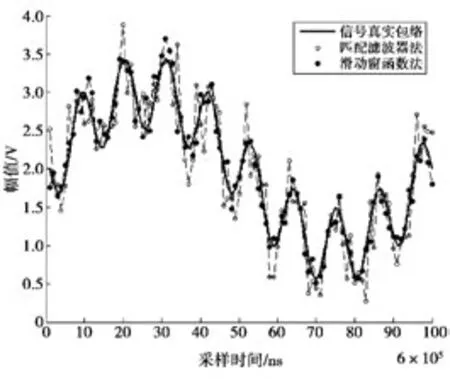
图4 一个周期内2种方法检测到的峰值点比较Fig.4 Comparison of a cycle of points from diverse detection method

10 dB信噪比情况下，分别利用匹配滤波器法与滑动窗函数法获得的周期性峰值点进行最小二乘拟合估计方位，结果如图5所示。可以看出，滑动窗函数法在10 dB功率信噪比情况下，方位估计误差能抑制在0.5°范围内，满足塔康系统方位误差为2°的要求，其结果优于匹配滤波器法。同时以滑动窗函数的峰值数据为基础，分别采用最小二乘拟合与二次迭代的最小二乘法估计方位，结果如图6所示，由图6可知，2种方法都能满足塔康系统要求，但后者的方位数据精度和稳健性更优，这是由于二次迭代把少数偏差大的峰值点滤除了。

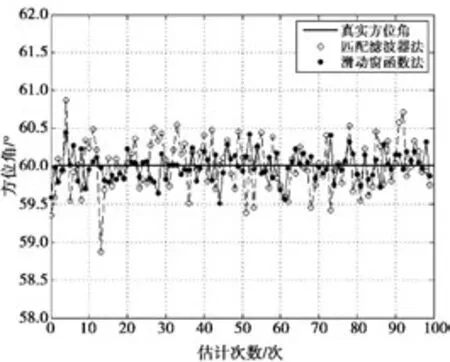
图5 不同检测方法获得的峰值点估计方位比较Fig.5 Comparison of azimuth estimation from diverse detection method

图6 不同拟合方法估计方位比较Fig.6 Comparison of azimuth estimation from diverse fitting method

5 结束语

以数字化的塔康系统为基础，针对峰值检测与方位估计，分别提出了滑动窗函数法与二次迭代最小二乘法。滑动窗函数法能有效检测脉冲并精确估计峰值。二次迭代最小二乘法是对一般最小二乘算法的优化，能较好地平滑拟合出来的包络。综合仿真结果可知，在10 dB信噪比情况下，本文所提方法的误差能抑制在0.5°以内，满足塔康系统方位误差为2°的要求。

［1］CHRESTOPHER E J.Electronically scanned TACAN antenna［J］.IEEE Transactions on Antennas Propagation，1974，22(1):12-16.

［2］SHESTAG L N.A cylindrical array for the TACAN system［J］.IEEE Transactions on Antennas Propagation，1974，22(1):17-25.

［3］张忠心，李晓明，张景伟.无线电导航理论与系统［M］.西安:陕西科学技术出版，1998:29-108.

ZHANG Zhongxin，LI Xiaoru，ZHANG Jingwei.Radio navigation theory and system［M］.Xi＇an:Shanxi science and technique publishing house，1998:29-108.

［4］田孝华，李睿，王维康.有效估计塔康测距信号多径时延的方法［J］.电子与信息学报，2010，32(9):2273-2276.

TIAN Xiaohua，LI Rui，WANG Weikang.An efficient time delay estimation algorithm for multipath signal of distance signal in TACAN system［J］.Electronics＆Information Technology，2010，32(9):2273-2276.

［5］龚成，郭英，齐子森.塔康导航系统机载中频信号数字化技术［J］.空军工程大学学报:自然科学版，2008，19(5):29-32.

GONG Cheng，GUO Ying，QI Zisen.Digital implement technology of TACAN IF signal［J］.Journal of Air Force Engineering University:Natural Science Edition，2008，19(5):29-32.

［6］王维康，张斌，李睿，等.塔康系统输出参数的精确测量方法研究［J］.电光与控制，2010，17(7):78-82，91.

WANG Weikang，ZHANG Bin，LI Rui，et al.Accurate measurement of TACAN output parameters［J］.Electronics Optics＆Control，2010，17(7):78-82，91.

［7］陈坤，田孝华，赵颖辉，等.塔康包络检测与方位估计算法研究［J］.电光与控制，2014，21(4):92-96.

CHENG Kun，TIAN Xiaohua，ZHAO Yinghui，et al.On TACAN envelope detection and azimuth estimation algorithm［J］.Electronics Optics＆Control，2014，21(4):92-96.

［8］陈坤，田孝华，赵颖辉，等.基于最小二乘迭代算法精确估计塔康方位参数［J］.科学技术与工程，2013，13(15):4176-4179.

CHENG Kun，TIAN Xiaohua，ZHAO Yinghui，et al.Accurate estimation for TACAN azimuth based on iterative least square algorithm［J］.Science Technology and Engineering，2013，13(15):4176-4179.

［9］彭大国，李治安，李晓明，等.塔康高精度测角及抗野值研究［J］.重庆邮电大学学报:自然科学版，2014，26(4):483-487.

PENG Daguo，LI Zhian，LI Xiaoming，et al.Accurate angle measuring and outliers restraining of TACAN［J］.Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition，2014，26(4):483-487.

［10］张浩杰，李晓明，裴文林.基于中频数字化技术的塔康测角方法研究［J］.现代防御技术，2012，40(3):67-71.

ZHANG Haojie，LI Xiaoru，PEI Wenlin.Angle measuring of TACAN based on IF digital technique［J］.Modern Defence Technology，2012，40(3):67-71.

［11］王鼎，章小梅，栾宝宽.塔康地面信标半幅探测电路对测距精度的影响分析［J］.现代导航，2014，4(2):117-120.

WANG Ding，ZHANG Xiaomei，LUAN Baokuan.Analysis of effect of halfamplitude detection circuit on measuring accuracy in TACAN beacon［J］.Modern navigation，2014，4(2):117-120.

［12］孙博，冯永浩，卢虎，等.一种塔康信标扩展数据广播功能的方法［J］.空军工程大学学报:自然科学版，2009，37(4):860-863.

SUN Bo，FENG Yonghao，LU Hu，et al.A Method of Adding Data-broadcast Function on Tacan Beacon［J］.Journal of Air Force Engineering University:Natural Science Edition，2015，16(4):80-83.

［13］应娜，赵晓晖，董婧，等.一种谐波正弦语音模型的最佳相位估计算法［J］.电子学报，2009，37(4):860-863.

YING Na，ZHAO Xiaohui，DONG Qian，et al.An algorithm of optimal phase esti-mation in harmonic sinusoidal speech model［J］.Chinese Journal of Electronics，2009，37(4):860-863.