利用星载GPS数据进行海洋2A卫星快速精密定轨
2015-12-15郭南男周旭华
郭南男,周旭华,吴 斌
(1.中国科学院上海天文台,上海200030;2.中国科学院大学,北京100049)
0 引言
海洋2A(HY2A)是我国第一颗海洋动力环境卫星。高精度且快速的轨道确定是HY2A卫星完成监测和调查海洋环境计划任务的关键。为满足厘米级的精密定轨需求,HY2A卫星上装载了星载GPS接收机、DORIS接收机、SLR反射棱镜三种精密跟踪系统。星载GPS、DORIS和SLR三种数据可作为独立或联合手段实现其精密定轨[1-3]。当前,除CNES外,国内还有四个单位参与其精密定轨工作,确定的轨道径向精度为1~2厘米,三维位置精度优于10厘米[2-3]。虽然定轨精度较高,但确定的轨道时延约为一天,影响了HY2A卫星的快速应用。
基于星载GPS非差动力学定轨,其轨道确定的时效性受两个因素制约,一是GPS精密星历和钟差产品获取的时延,另一个是卫星实测数据从星上传到数据处理中心的时延[4]。通过对卫星精密轨道拟合和外推虽可以得到实时的卫星轨道,但外推的轨道精度难以保证,如高鹏等[5]采用切比雪夫曲线和最小二乘曲线拟合HY2A卫星精密轨道,表明要保证厘米级的轨道精度,外推时间不能超过120秒。通过单点定位软件可以实时确定出卫星位置,但轨道精度差,一般为米级。使用高精度GPS事后精密星历和钟差完成的精密定轨,轨道精度高,但时效性差,不能满足某些低轨卫星的快速定轨需求。使用IGS提供的超快速GPS星历IGU虽可实现快速定轨,但IGU提供的钟差采样率低,定轨精度较差。为此,中科院上海天文台建立了GNSS数据中心,定时发布SHR快速、SHU超快速精密星历和30秒采样率的钟差产品[6],虽然SHU事后星历可以超快速获取,仍存在几小时的时延,且并未提供预报星历,无法进一步的获取更短时间延迟的精密星历。因此提出联合SHU超快速精密星历和IGU预报星历方案,为低轨卫星快速定轨和满足诸如快速大气监测等科学任务提供服务。
本文利用2014年1月1日-31日HY2A卫星的星载GPS实测数据,采用非差动力学方法,使用SHA和IGS数据分析中心发布的不同时延和精度的星历及钟差产品,对HY2A卫星进行快速精密定轨研究,并以CNES精密轨道检验和SLR检核,评价其定轨精度,确定最优的快速精密定轨方案,为实施我国后续卫星计划提供参考。
1 观测方程
基于星载GPS观测数据进行精密定轨时,以相位和伪距观测值作为基本观测量进行非差动力学定轨。根据GPS伪距和相位观测值,可建立以下观测方程:

分析上述观测方程,要得到低轨卫星精密轨道,必须消除观测中的一些误差。如GPS卫星钟差δts采用IGS或其它数据处理中心发布的GPS卫星钟差产品;接收机钟差δtr作为历元参数进行求解;相对论延迟改正δρrel可以通过模型进行准确修正;布的相位中心改正;电离层延迟改正δρion则与低轨卫星的位置相关且无法建立全球统一准确的数学模型,非差动力学定轨中采用无电离层组合模型来削弱电离层延迟的影响。其中双频无电离层伪距组合P3和相位组合L3分别可表示为:
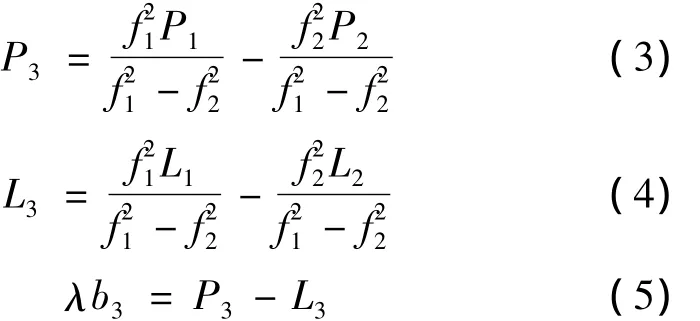
式中:b3为无电离层相位组合的模糊度,此时不再具有整数特性,并当作未知数求解。在这里利用双频伪距无电离层组合主要用于周跳探测和初始模糊度的确定,在不存在相位周跳的时间段内,上述b3只有随机的噪声误差,对其在无相位周跳的时间内进行平均可以提高该量精度。在探测到相位周跳后,重新计算模糊值。
结合式(2)、(4)、(5)形成基于双频无电离层相位组合观测值的观测方程:

各个参数的意义同式(2)。
2 定轨策略
星载GPS非差动力学定轨采用批处理算法,包括数据预处理(如野值剔除、周跳探测、LC组合的初始模糊度计算等)、卫星运动方程和变分方程的数值积分、卫星摄动和动力学参数偏导计算、法方程的计算及其求逆、叠代循环控制等。其中力学模型的选择和待解参数的设置是动力学定轨的关键[7-9]。表1给出了轨道计算中涉及的力学模型及待解参数的设置。
3 GPS星历产品及分析
3. 1 星历产品的选取
目前大多数的GNSS产品都由IGS数据分析中心提供,发布的精密轨道产品是多个数据处理中心结果的综合。中国科学院上海天文台(SHAO)为满足低轨卫星快速定轨等需求,建立了GNSS分析中心,定时提供快速星历SHR、超快速星历SHU、钟差和 ERP 等产品[10]。
当前,各个数据分析中心的GNSS产品主要区别在于时间延迟、更新周期、产品精度和钟差的采样率。SHA分析中心的超快速星历产品SHU与IGS分析中心的超快速星历IGU相比,具有相近的时间延迟及星历精度,且具有30 s的高采样率钟差,但没有预报星历。而IGU星历每个文件由48小时的星历组成,前24小时为实测星历数据,后24小时为预报星历数据,均对应15 min采样率的钟差产品。为了方便表示,文中用IGU表示IGU实测星历部分,可事后3-9小时获得,包括轨道和钟差信息;用IGU-P表示IGU预报星历部分,同时包括轨道和钟差信息。SHU表示SHA数据分析中心发布的超快速精密星历和钟差产品,可事后6小时获取。表2给出了所采用的星历和钟产品精度、时间延迟以及钟差的采样率等相关信息。

表1 HY2A卫星精密定轨中的力学模型与解算参数Table 1 Models and parameters used in orbit determination for HY-2A

表2 不同时间延迟和精度的GPS星历和钟差产品Table 2 Latency and accuracy of different GPSorbit and clock products
3. 2 精密星历产品的内插
IGS等数据分析中心提供的精密星历为15 min间隔,而星载GPS接收机输出的观测数据采样率通常为几秒,甚至更密,因此在定轨中需要对GPS精密星历进行内插。彭冬菊等研究表明[11],如果选择适当的拟合函数,可以内插出精度很高的轨道,10阶Chebyshev多项式插值精度为毫米级,拟合精度与多项式阶数选择有关。
非差动力学定轨除了依赖于高精度的GPS卫星轨道外,还依赖于高精度的GPS钟差。由于非差动力学定轨中GPS钟差不能作为待估参数也不能通过差分进行消除,对定轨结果影响较大。为了提高定轨精度,需要得到尽可能准确的GPS钟差。由于GPS卫星钟差的大小与钟的特性(如频偏、频漂等)相关,一般采用线性拟合或低阶多项式方法拟合。洪樱等[12-13]研究表明,采用8阶滑动Lagrange拟合方法对5 min和30 s的GPS钟差产品进行拟合以及采用3阶滑动Lagrange拟合对15 min的GPS钟差产品进行拟合,拟合效果最好。
4 精密定轨
本文通过对IGS和SHA数据分析中心星历产品的定轨精度进行对比分析,验证采用两类星历组合(SHA分析中心的超快速星历SHU和IGS预报星历IGU-P)可以实现HY2A卫星的高精度快速定轨,并通过与CNES精密轨道的比较以及SLR检核的方法,对轨道精度进行了评估和分析。
4. 1 不同星历产品定轨结果的对比
利用2014年1月1日-31日HY2A卫星实测数据进行精密定轨,以CNES发布的事后精密轨道作为参考轨道,研究不同星历产品确定的轨道精度。三种方案选择的星历产品分别为:(1)IGU超快速星历,时延3-9小时,星历和钟差采样率均为15 min;(2)SHU超快速星历产品,时延6小时,星历采样率为15 min,钟差采样率为30 s;(3)IGS事后精密星历产品,时延为12-18天,星历采样率为15 min,钟差采样率为30 s。图1以2014年1月1日为例,定量估计星历(钟差)产品IGU、SHU及IGS的定轨精度。横轴为时间,单位为小时;纵轴为定轨结果的径向R、切向T、法向N与参考轨道对应方向的差值,单位为厘米。
从图1可以得到,分别使用IGS、SHU和IGU产品确定2014年1月1日的精密轨道,对比于参考轨道,在R方向的 RMS分别为1.21 cm、1.22 cm 和2.62 cm,T 方向的 RMS 分别为 4.08 cm、4.38 cm和 6.90 cm、N 方向的 RMS分别为 2.14 cm、2.14 cm和2.99 cm。
图2为统计2014年1月1日-31日31天使用IGS、SHU与IGU三种不同星历产品确定的轨道与参考轨道在径向、切向、法向及三维位置之差的RMS。
从图2中可以得到,采用SHU星历(钟差)产品定轨结果,与参考轨道之差在径向、切向、法向RMS平均值分别为 1.34 cm,3.85 cm,2.02 cm,三维位置RMS平均值为4.57 cm,与IGS事后精密星历产品定轨结果(径向:1.28 cm,切向:3.78 cm,法向:1.99 cm,三维:4.48 cm)非常接近,优于用 IGU 精密星历产品的定轨结果(径向:2.64 cm,切向:6.71 cm,法向:3.64 cm,三维:8.17 cm)。表明SHA发布的超快速星历SHU的定轨精度优于相同时延的IGU星历结果,与时延约12天的IGS事后精密星历产品结果精度相当。
4. 2 IGS预报星历定轨结果与预报轨道的比较

图1 与CNES精密轨道比较,不同GPS星历产品定轨结果的残差图Fig.1 Differences between our solution by using different GPSephemeris products and CNES
轨道预报可以实时确定出低轨卫星的轨道,但卫星所处的空间环境复杂,预报轨道精度通常较低。为获取快速精密轨道,也可采用IGS提供的IGU-P预报星历通过精密定轨得到。下面以法国CNES发布的事后精密轨道作为参考轨道,通过对比研究预报星历的定轨精度和预报轨道精度。采用两种方案分别是:(1)使用IGU-P星历产品对HY2A卫星进行弧长6小时的精密定轨;(2)使用SHU星历产品在精密定轨的同时完成6小时轨道预报;再评价IGU-P定轨结果和SHU的预报轨道结果。表3用列表形式给出了2014年1月1日到10日共10天的两种轨道与参考轨道在径向、切向、法向以及三维位置之差的RMS。

图2 不同GPS星历产品定轨结果的比较Fig.2 Orbit accuracy by using different GPS ephemeris products
从表3可以得到,IGU-P计算的10天轨道与参考轨道在径向、切向、法向以及三维位置之差的平均RMS 分别为 4.09 cm、8.95 cm、5.31 cm、11.38 cm,优于利用SHU进行轨道预报结果(径向:6.84 cm,切向:16.11 cm,法向:4.01 cm,三维:18.03 cm),表明利用IGU-P星历可以实现径向精度优于5 cm的HY2A卫星轨道。为了更加清楚的比较两种方案的总体精度,图3给出使用IGU-P计算的6小时HY2A卫星轨道和使用SHU进行预报的轨道与参考轨道的三维位置之差的RMS,时间跨度为2014年1月1日到1月31日。图中横轴为年积日,纵轴为三维位置RMS,单位为cm。从图3可以看出,使用IGU-P星历产品进行6小时精密定轨的三维位置精度明显优于SHU星历6小时的短弧预报轨道。
综合以上结果可见,将SHU星历产品和IGU-P星历产品进行组合定轨,可以得到较高精度的HY2A快速轨道。本文中将24小时弧长的HY2A快速轨道分为18小时弧长的SHU超快速精密星历定轨结果与6小时弧长的IGU-P定轨结果的组合。对比CNES精密轨道,得到2014年1月确定HY2A快速轨道的三维位置平均精度约为6 cm,满足实际应用的需求。当然,该轨道是两部分组合形成的,两者精度差异较大,实际应用中应区别对待。

表3 预报星历定轨结果和预报轨道的比较(RMS:/厘米)Table 3 Compare orbit prediction with orbit determination by using predict ephemeris(RMS:/cm)

图3 预报轨道和预报星历的定轨结果比较Fig.3 Compare orbit prediction with orbit determination by using predict ephemeris
4. 3 快速轨道的SLR检验
HY2A卫星上不仅搭载了星载GPS接收机,还配备了激光反射器,且激光测距技术(SLR)是独立于GPS的另一精密测距系统。SLR的观测精度优于1 cm,是目前检验卫星定轨结果的主要手段[14]。图4为2014年1月1日至31日组合轨道中SHU和IGU-P星历产品定轨结果分别对应的SLR检核残差。由于弧长6小时轨道对应的高仰角SLR数据很少,因此截止高度角设定为20度,即站星间高度角大于20度的SLR数据参与检核。从图4可以看出,基于SHU和IGU-P星历产品确定的轨道在测距方向残差RMS的平均值分别为2.9 cm和4.8 cm,表明结合使用组合星历产品可以得到厘米级精度的HY2A快速精密轨道。
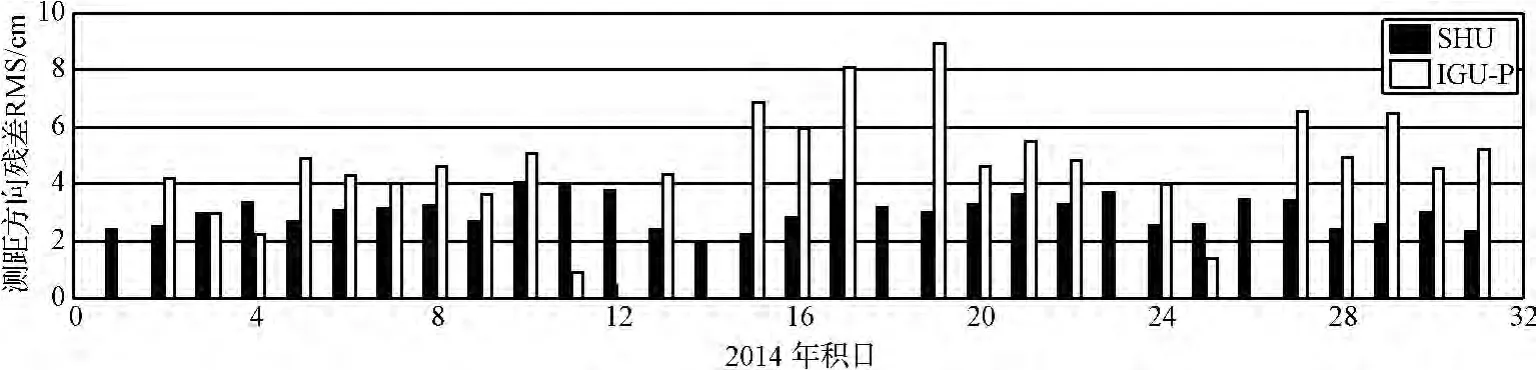
图4 SLR检核SHU和IGU-P星历产品的定轨结果Fig.4 SLR residuals for orbits by using SHU and IGU-P ephemeris products
5 结论
基于2014年1月星载GPS实测资料,结合GPS精密星历和钟差产品,采用非差动力学方法,对HY2A卫星进行了快速定轨研究,结果表明:
(1)SHA发布的超快速精密星历产品SHU与采用IGS事后精密星历产品确定的HY2A轨道精度相当,两者三维位置精度之差小于5 mm。SHU的实时性优于IGS事后精密星历。
(2)使用SHU星历和钟差产品实现的事后6小时HY2A卫星快速轨道与CNES发布的精密轨道在径向、切向、法向以及三维位置方向RMS的平均值分别为1.34 cm,3.85 cm,2.02 cm,4.57 cm,优于相同时间延迟的IGU星历产品的定轨结果(径向:2.64 cm,切向:6.71 cm,法向:3.64 cm,三维:8.17 cm)。
(3)用IGU-P星历产品对HY2A卫星进行6小时精密定轨,其结果与CNES发布的精密轨道在径向RMS约为4 cm,三维位置RMS约为12 cm,优于SHU的6小时短弧段预报轨道结果(径向:7 cm,三维位置:21 cm)。
(4)提出超快速精密星历产品SHU和IGU-P星历产品组合进行HY2A卫星的快速定轨,可以实现在仅存在数据传输延迟的情况下获得厘米级精密轨道。
(5)用SLR数据检核组合超快速星历SHU和预报星历IGU-P确定的轨道,发现两者在测距方向残差RMS的平均值分别为2.9 cm和4.8 cm,表明使用SHU和IGU-P可以确定出测距方向厘米级精度的卫星轨道。可见,联合使用SHU超快速星历产品和IGU预报星历产品形成的HY2A卫星快速轨道,能有效地提高HY2A卫星轨道的时效性,同时提高海洋环境监测和海洋灾害预警数据的准确性和时效性,对充分发挥海洋卫星应用功能具有重要意义。
[1] Zhao G,Zhou X H,Wu B.Precise orbit determination of Haiyang-2 using satellite laser ranging [J].Chinese Science Bulletin,2013,58(6):589-597
[2] 朱俊,王家松,陈建荣,等.HY-2卫星DORIS厘米级精密定轨[J].宇航学报,2013,34(2):163-169.[Zhu Jun,Wang Jia-song, Chen Jian-rong, et al. Centimeter precise orbit determination for HY-2 via DORIS[J].Journal of Astronautics,2013,34(2):163 -169.]
[3] 郭靖,赵齐乐,李敏,等.利用星载GPS观测数据确定海洋2A卫星cm级精密轨道[J].武汉大学学报.信息科学版,2013,38(1):52 - 55.[Guo Jing,Zhao Qi-le,Li Mi,et al.Centimeter level orbit determination for HY2A using GPS data[J].Geomatics and Information Science of Wuhan University,2013,38(1):52 -55.]
[4] Wermuth M ,Huschild A,Montenbruck O,et al.Terra SARX precise orbit determination with real-time GPS ephemerides[J].Advances in Space Research,2012,50(5):549-559.
[5] 高鹏,乔学军,范城城.HY-2卫星精密轨道拟合与外推的两种方法比较[J].海洋测绘,2013,33(4):58-61.[Gao Peng,Qiao Xue-jun,Fan Cheng-cheng.Comparison of two methods of HY-2 satellite precision orbit fitting and extrapolation [J].Hydrographic Surveying and Charting,2013,33(4):58 -61.]
[6] Chen JP,Zhang Y Z,Zhou X H,et al.GNSSclock corrections densification at SHAO:from 5min to 30s[J].Science China Physics,Mechanics& Astronomy,2014,5(1):166-175
[7] Švehla D,Rothacher M.Kinematic and reduced-dynamic precise orbit determination of low earth orbiters[J].Advances in Geosciences.2003,1:47 -56
[8] Visser P,Van J.Aiming at a1-cm orbit for low earth orbiters:reduced-dynamical and kinematic precise orbit determination[J].Space Science Review,2003,108:27 -36
[9] Peng D J,WU B.Zero-difference and single difference precise orbit determination for LEO using GPS[J].Chinese Science Bulletin,2007,52(15):2024-2030
[10] Chen J P,Wu B,Hu X G,et al.SHA:The GNSS analysis center at SHAO [C].China Satellite Navigation Conference 2012 Proceedings,Guangzhou,May 16 -19,2012
[11] 彭冬菊,吴斌.GPS星历对LEO星载GPS精密定轨精度的影响[J].天文学报,2008,49(4):434-443.[Peng Dongju,WU Bin.The impact of GPS ephemeris on the accuracy of precise orbit determination for LEO using GPS[J].Acta Astronomica Sinica,2008.49(4):434 -443.]
[12] 洪樱,欧吉坤,彭碧波.GPS卫星精密星历和钟差三种内插方法的比较[J].武汉大学学报.信息科学版,2006,31(06):516 - 518.[Hong Ying,Ou Ji-kun,Peng Bi-bo.Three interpolation methods for precise ephemeris and clock offset of GPSsatellite[J].Geomatics and Information Science of Wuhan University,2006,31(06):516 -518.]
[13] 叶聪云,罗涛,陈远,等.精密卫星钟差的内插方法研究[J].测绘信息与工程,2008,01:11-13.[Ye Cong-yun,Luo Tao,Chen Yuan ,et al.On interpolation of satellite clock bias[J].Journal of Geomatics,2008,01:11 -13.]
[14] Barlier F,Berger P,Bonnefond P,et al.Laser-based validation of GLONASS orbits by short-arc technique [J].Journal of Geodesy,2001,75(11):600–612
