自主机动飞网机器人动力学建模与网型保持方法

孟中杰，黄攀峰

(1.西北工业大学航天学院智能机器人研究中心，西安710072;2.航天飞行动力学技术国家级重点实验室，西安710072)

0 引言

近年来，随着航天技术的不断发展，各国对于故障卫星维修、近距离目标捕获、轨道垃圾清理等在轨服务技术的需求日益迫切［1］。

自主机动飞网机器人(简称飞网机器人)是一种由柔性网和多个自主机动单元组成的新型空间机器人。在机动单元的控制下，它可以逼近任意空间目标，由柔性网覆盖捕获目标，然后进行操作、变轨等。飞网机器人在安全性、灵活性、可靠性等具有传统的空间机器人所无法比拟的优势，在轨道垃圾清理、失效卫星捕获等空间任务中有着非常广泛的应用前景。在操作任务中，飞网机器人需要保持固定的网型，但是由于重力梯度、科氏力等的作用，柔性飞网保持固定网型十分困难。另外，飞网机器人的机动也大大提高其网型保持的难度。

在与飞网机器人类似的空间柔性网系统动力学与控制研究方面，Gärdsback M等研究了一种空间自旋网结构的动力学和最优展开控制问题［2－3］。翟光、于洋、李京阳等人的研究对象是一种由平台、系绳、质量块、网组成空间飞网结构。针对这种飞网，Mankala等研究了动力学建模与仿真问题［4］，Zhai等研究了结构设计与动力学问题，并设计了一种利用系绳张力和推力的反馈控制器，保证飞网能够有效地飞向目标［5－7］，但是，在 Mankala和 Zhai的研究中，研究重点放在平台、系绳、末端执行器组成的系统动力学研究上，飞网结构被假设为质点。于洋等研究了飞网的抛射动力学问题［8］。李京阳等分析了空间飞网的松弛模型和柔性模型，得出了松弛模型更接近真实飞网的结论［9］。陈钦等研究了空间飞网的设计，并利用集中质量法，将系绳质量集中在两端节点处，建立了“节点+轻质弹性杆”的飞网数学模型［10－11］。马骏等利用类似的方法研究了一种带四个自主机动单元的空间绳网机器人动力学建模和仿真问题［12］。但是，柔性网的编织特点造成各节点间的距离较小，而轻质弹性杆的刚度极大，“节点+轻质弹性杆”的飞网模型在计算时需要极小的步长。另一方面，上述模型均是针对仿真分析的数学模型，利用该模型很难进行针对性的控制器设计。

针对该问题，本文提出一种面向控制的自主机动飞网机器人的动力学建模方法，并针对性的设计其空间任务过程中的网型保持方法。

1 自主机动飞网机器人动力学建模

在动力学建模时，采用如下基本假设:

(1)忽略自主机动单元体积，将其假设为质点;

(2)飞网机器人运行在圆轨道上。

1. 1 飞网机器人的描述

在动力学建模之前，需要首先研究飞网机器人的表达方式。本文采用无向图G=(V，E)描述其拓扑结构。其中，V为非空的顶点集，包括自主机动单元、系绳交叉的编织点及人为选择的系绳节点，设n为V中顶点数。E为V中元素构成的二元组的集合，称为边集，包含飞网机器人各绳段，描述了各节点间的连接关系，设c为E中所有边的个数。在实际建模中，可采用邻接矩阵表达无向图。将邻接矩阵中表示连接的元素1用系绳的自然长度lij代替。则n×n维邻接矩阵A的元素aij为:

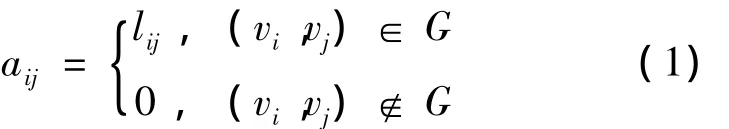
1. 2 空间系绳动力学建模

系绳的模型由简单到复杂可以分为轻质刚性杆模型、刚性杆模型、轻质弹性杆模型、弹性杆模型、株式模型、有限元线段模型、考虑弹性/弯曲/扭转/剪切的模型等［13－14］。Buckham B 研究了低张力系绳的应用，并通过实验数据和仿真数据的对比，校验了将系绳质量集中在节点处的方法适合低张力系绳的数值仿真［15］。因此，本文采用集中质量法建立系绳模型，系绳的非线性本构关系为:

式中:N为系绳张力，E为系绳的杨氏模量，A为系绳的截面积，ε为系绳应变，τ为系绳张力的单位方向向量。

空间系绳普遍采用KEVLAR等合成纤维编织而成，杨氏模量E极大，可达130 GPa。以1 mm直径的KEVLAR系绳段为例，其弹性系数高达105。而飞网机器人系绳中的张力与网大小、机动单元的推力相关，一般较小。以10 N张力为例，系绳应变仅为10－4，且沿系绳方向具有极高频的振动。这也是“节点+轻质弹性杆”的飞网模型在计算时需要极小的步长，以保证仿真稳定的根本原因。为解决这一问题，假设EA→+∞，ε→0。此时，式(2)已不能用来计算系绳的张力。分析不可伸长系绳的特点，并借鉴文献［16］中刚体接触问题的处理方法，引入间隙函数和约束反力描述系绳的非线性本构关系。

间隙函数:

约束反力:

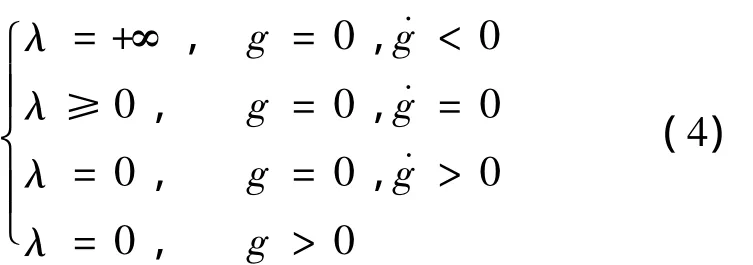
式中:Ri，Rj为系绳上两节点的位置，l0为两节点间系绳的自然长度。约束反力即近似描述了系绳中的张力。

将飞网机器人系统的间隙函数和约束反力写成向量形式:

1. 3 飞网机器人的动力学建模

本节利用Hamilton原理建立自主机动飞网机器人的动力学模型。在集中质量和系绳不可伸长假设下，飞网机器人的拉格朗日函数L仅包括各节点的动能与势能。在地心惯性系下:

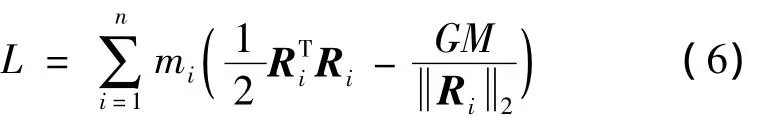
式中:mi为节点质量，Ri为节点在地心惯性系下的位置，G表示万有引力常数，M表示地球的质量。

系统的非保守力包括各节点的控制力Fi和约束反力。非保守力做的功为:

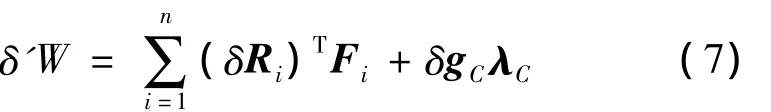
利用广义Hamilton原理:

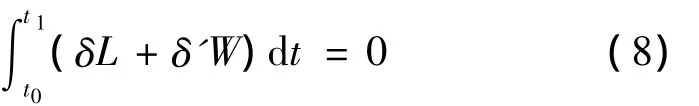
可推导飞网机器人的动力学模型。

Ri包含飞网机器人的轨道运动和相对运动，很难直接分析机器人的形状保持情况。在圆轨道假设下，选取飞网机器人轨道或附近轨道上一点为虚拟目标，建立目标轨道系，将飞网机器人模型转换到目标轨道系下，并利用Hill方程化简，得:

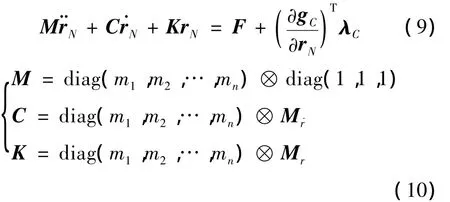
式中:ω为虚拟目标的平均轨道角速度。

另外，不可伸长的系绳还具有一种独特的速度跳变现象。以两节点、单系绳结构为例，当t－时刻，两节点间距离达到标称长度(即g=0)，但两节点相对速度不为0，且有相互远离的趋势(即˙g＜0)时，系绳突然绷紧，系绳中张力极大，使得两个节点在t+时刻具有了沿系绳方向一致的速度，这就是速度跳变现象。下面对不可伸长系绳的速度跳变进行动力学建模。

将动力学方程(9)在时间区间［t－，t+］积分，得:

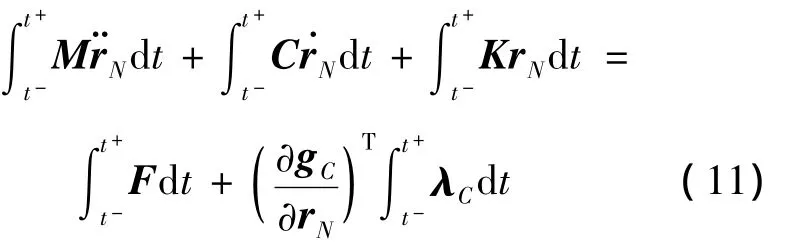
时间区间［t－，t+］为瞬时过程，节点位置矢量、速度矢量、控制力均为有限值，约束反力为无穷大，式(11)左侧后两项和右侧第一项均为0，设约束反力在［t－，t+］的积分为 ΛC，式(11)可化简为:

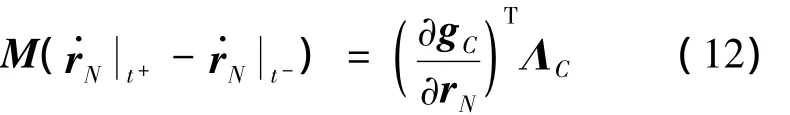
式中:ΛC为积分区间［t－，t+］内约束反力产生的动量，未产生速度跳变系绳约束反力产生的动量为零。刻产生速度跳变现象系绳的间隙函数。在t+时刻，产生速度跳变现象的系绳间隙函数为零。即:

联立式(12)(13)，可得速度跳变后的系统状态。

1. 4 飞网机器人动力学模型的解算

飞网机器人的动力学模型(9)中包含未知项约束反力λC，而λC与位置项rN，速度项˙rN，加速度项¨rN隐性相关，但式(4)仅给出其定性表达式，不能应用于动力学模型解算。

在系统动力学求解时，位置项、速度项已知，即g，˙g已知。若g＞0∪g=0，˙g＞0，约束反力λ=0;若g=0，˙g=0，需要进一步求解λ。

设满足g=0，˙g=0条件的间隙函数和约束反力为m个，将其写成向量形式¯λC，¯gC。利用间隙函数定义，对¯gC求两次导得:

式中:h(rN，˙rN)为不含二次项的余项，在动力学解算时为已知项。

将动力学方程(9)代入式(14)，得:

式中:MR是¯λC到λC的转换矩阵，为c×m维。

具有不等式约束的隐式方程(15)是一个典型的线性互补问题，最常用的求解算法是Lemke算法。详细的求解步骤参见文献［17］。

飞网机器人动力学模型的解算流程如图1所示。详细的解算步骤为:

(1)计算各系绳的间隙函数，根据间隙函数及其微分将间隙函数¯gC及约束反力¯λC分离;

(2)利用Lemke算法求解式(15)，计算当前时刻的约束反力;

(3)利用式(9)，计算当前时刻的加速度项;

(4)利用四阶龙格库塔法进行积分运算，得到下一时刻的系统状态;

(5)判断是否存在速度跳变现象;若存在，联立式(12)(13)，求解速度跳变后的系统状态;

(6)转到第一步，循环求解下一时刻的动力学。

图1 自主机动飞网机器人模型解算流程Fig.1 Solution process for the dynamic model of AMNR

2 自主机动飞网机器人网型保持控制

由于重力梯度力、科氏力、系绳张力的作用，飞网机器人不能自动保持其固有形状，尤其是在轨道机动过程中，控制力仅作用在自主机动单元上，对飞网形状影响极大，因此需要进行网型保持控制。

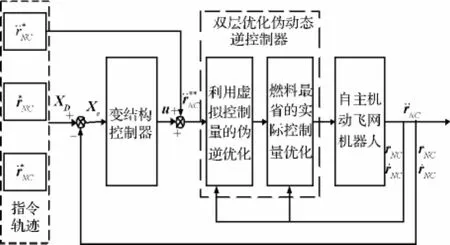
系统动力学模型存在未知的约束反力项λC仅能通过构建线性互补问题求解。并且，λC属于快变项，很难利用神经网络等方法通过学习表达。这给控制系统设计带来了极大的困难。速度跳变现象的存在也加剧了控制系统设计的难度。借鉴单面约束的刚体接触控制思想，本文提出一种“双层优化伪动态逆内环+变结构控制外环”的设计思想，如图2所示。

在伪动态逆控制中，优化目标是求取满足动力学约束的控制力，使得实际加速度与期望加速度之间的偏差最小。针对约束反力λC的存在，本文提出一种两层优化的策略。首先，设计虚拟控制量

将式(9)转化为线性方程。在求其伪逆时，需要考虑不等式约束≥0。设飞网机器人可直接控制的节点位置为rNC。

然后，利用虚拟控制量求解实际控制量F。以最省能量为目标，重新构建优化问题。

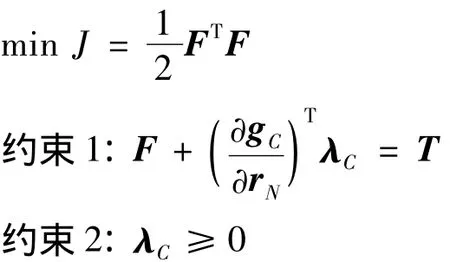
考虑到伪逆与真实逆的偏差，需要在伪逆的外环加入控制器。本文选择变结构控制器。经过伪逆控制器后，系统动力学模型可写为:

式中:

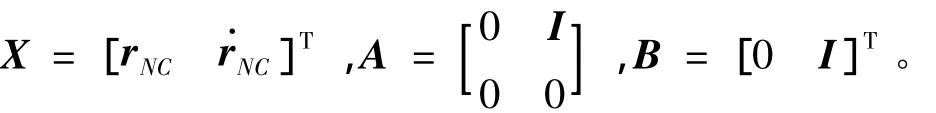
设期望指令为XD，跟踪误差Xe=XD－X。

设计积分型切换函数为:

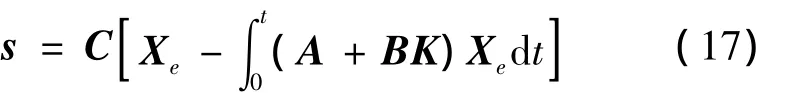
式中:C为正常数组成的矩阵，K为状态反馈增益矩阵。设计滑模控制器为:

式中:B+为B的Moore－Penrose逆，f＞0。下面进行稳定性证明。

因此，在控制器作用下，系统一致渐近稳定。

为减弱控制过程中的抖动，选用饱和函数sat(s)代替符号函数sgn(s)，得到最终的变结构控制律。设Si表示S的元素，sat(S)的各元素表示为:

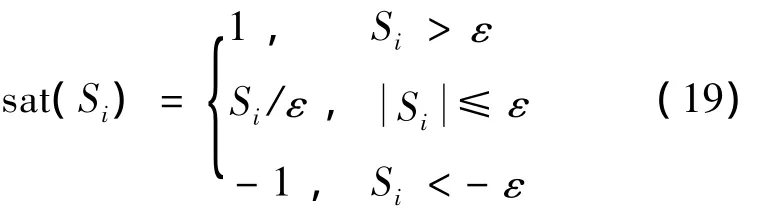
图3 自主机动飞网机器人实例Fig.3 An example of MNR

3 仿真算例与分析

以图3所示飞网机器人为例。该机器人包含5个自主机动单元和12个系绳节点。将自主机动单元和系绳编织节点作为无向图的顶点，邻接矩阵为:

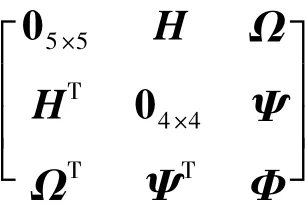
式中:Ψ是4×8的稀疏矩阵，其元素为:

Φ是8×8的稀疏矩阵，其元素为:

设系绳直径1 mm，杨氏模量130 Gpa，线密度4.5 g/m，自主机动单元质量 10 kg，轨道高度700 km，飞网机器人初速［1，0，0］m/s，设初始状态为绷紧状态，分别仿真无控和节点1施加［0.1，0，0］N恒推力两种情况，并与文献［12］中珠子模型进行对比，误差如图4、图5所示。可以看出，无控时，本文的数学模型与珠子模型仿真误差较小。施加恒推力时，由于实际系绳存在变形，误差比无控时大，但与整个系统相比，误差最大为万分之八。在时间对比上，珠子模型需要选择较小的步长(本文选择为2 ms)，以保证系统收敛，本文建立的模型可以选择较大步长(本文选择为500 ms)，时间消耗大大降低。

图4 无控时，两种模型对比Fig.4 Comparisons without control

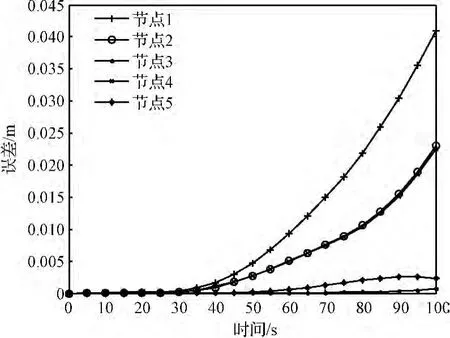
图5 节点1施加恒推力时，两种模型对比Fig.5 Comparisons with constant thrusts on node 1

下面进行控制器的仿真校验。设初始状态为绷紧状态，各自主机动单元具有［1，0，0］m/s初速，其余节点无初速。无控状态的仿真结果如图6所示。

可以看出:由于仅自主机动单元具有速度，其他系绳编织节点通过自主机动单元带动运行，飞网机器人轨道法向平面视图由“▽”变为“W”形状，且整体成收缩趋势。初始时刻处于轨道面内的节点1与节点3间距离由141.42 m减小为132.36 m，初始时刻处于轨道面外的节点2与节点4间距离由141.42 m减小为65.52 m，由节点1～节点4形成的最大开口面积由10000 m2减小为8672 m2。节点5运动速度大于编织节点，飞网机器人底部变为凹型。从飞网机器人轨道面看，飞网机器人沿轨道切向运动，由于科氏力的作用，其整体向 －Z方向偏移，且由于速度方向的偏移，沿轨道切向运动变慢。以节点5为例，在1 m/s的初速下，500 s内，其沿轨道 +X向仅运行276.56 m，同时，其沿轨道 －Z向运行198.03 m。因此，在飞网机器人沿切向机动时，需要进行网型保持与整体位置控制。

图6 自主机动飞网机器人无控飞行Fig.6 Ideal non－control motion of AMNR

以节点5为例，速度跳变前后的速度差如图7所示。可以看出:不可伸长系绳所特有的速度跳变现象一直存在于飞行过程。

图7 节点5速度跳变现象Fig.7 Velocity jump of node 5

选择控制器参数 K= － 0.03［I15，5I15］，C=115×30，f=0.1，设飞网机器人的期望状态为沿轨道X 向，以初速［1，0，0］m/s运行，仿真时间为 500 s，仿真结果如图8所示。可以看出:

(1)在控制器的作用下，飞网机器人整体沿轨道切向运动，未出现径向和法向的移动，以节点5为例，位置由初始［－1000，0，0］m 变为［－500.07，0.03，－0.02］m。

(2)飞网机器人整体形状保持良好;处于轨道面内的节点1与节点3间距离由141.42 m变为141.37 m，处于轨道面外的节点2与节点4间距离由141.42 m变为141.61 m，由节点1～节点4形成的开口面积由10000 m2变为100010 m2，变化率约为1‰。

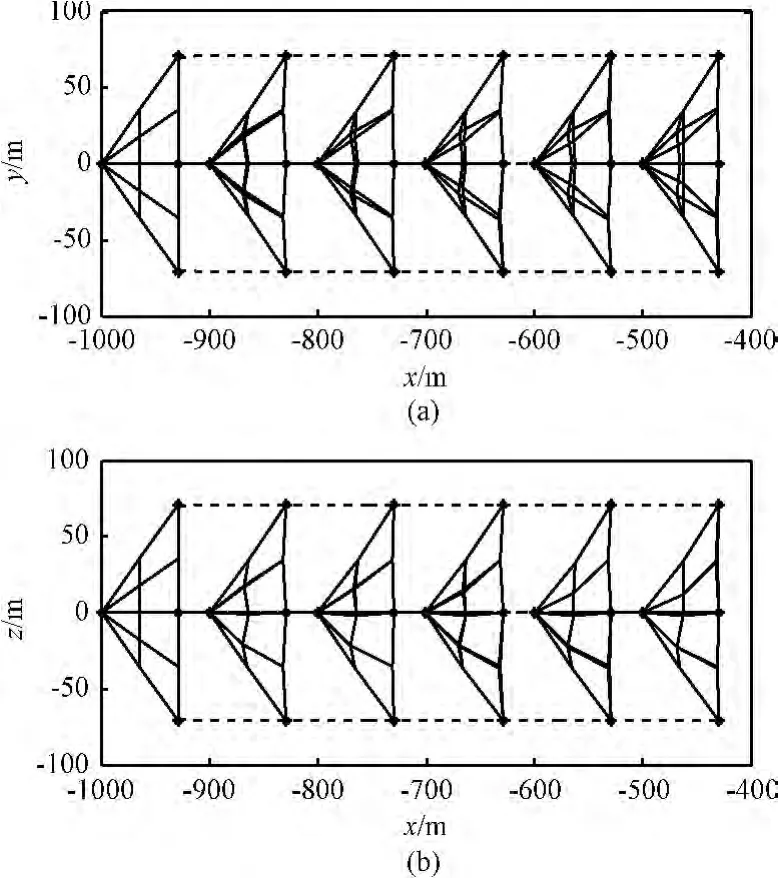
图8 自主机动飞网机器人有控飞行Fig.8 The motion of AMNR under the control

可见，本文设计的控制器能够使自主机动飞网机器人沿预定轨迹运动，并保持其网型。但是，由于仅五个自主机动单元有控制力，飞网机器人形状并不是严格未变化，在各节点间具有一定的变形。

以节点1与节点17间系绳为例，图9是无控飞行和有控飞行时，该系绳约束反力对比。在无控飞行时，由于仅自主机动单元具有初速，在发射后，由于系绳的牵拉，系绳具有一定的约束反力(最大约0.02 N)，直至各节点具备相同的运行速度后，各节点处于近似自由飞行状态、系绳约束反力近似为零。在有控飞行时，飞网机器人形状保持较好，为克服科氏力等影响，系绳中一直存在约束反力，约束反力最大约0.34 N。

图9 系绳约束反力对比Fig.9 Comparisons of constraint reaction forces

图10 自主机动飞网机器人机动飞行Fig.10 The orbit maneuver of AMNR under the control

假设根据任务需要，在任务初期，飞网机器人在以设定初速逼近目标的同时，需要在100 s内向+Z向机动75 m，设计机动过程，并利用本文设计的控制器进行200 s仿真，仿真结果如图10所示。可以看出，飞网机器人能够按设计的机动轨迹完成机动，且在机动过程中飞网机器人整体构型保持良好，验证了本文设计的飞网机器人控制及网型保持方法的有效性。

4 结论

针对自主机动飞网机器人的多节点编织特点，提出一种基于无向图的结构描述方法，然后利用间隙函数和约束反力，基于Hamilton原理建立数学模型，并设计了一种“双层优化伪动态逆内环+变结构控制外环”的网型保持方法。仿真结果表明:本文建立的数学模型精度与传统珠式模型相当，但计算速度快，计算稳定，不易发散;控制器能够在任务过程中有效保持飞网机器人的网型，且避免了飞网机器人的轨道径向移动。

［1］ 敬忠良，袁建平.航天器自主操作的测量与控制［M］.北京:中国宇航出版社，2011:493－518.

［2］ Gärdsback M，Tibert G.Optimal deployment control of spinning space webs and membranes［J］.Journal of Guidance，Control，and Dynamics，2009，32(5):1519 －1530.

［3］ Gärdsback M，Tibert G.Deployment control of spinning space webs［J］.Journal of Guidance，Control，and Dynamics，2009，32(1):40－50.

［4］ Mankala K K，Agrawal SK.Dynamic modeling and simulation of impact in tether net/gripper systems［J］.Multibody System Dynamics，2004，11(3):235 －250.

［5］ Zhai G，Qiu Y，Liang B，et al.System dynamics and feedforward control for tether－net space robot system ［J］.International Journal of Advanced Robotic Systems，2009，6(2):137－144.

［6］ Zhai G，Qiu Y，Liang B，et al.Research and design of orbital net－capture robot system ［C］.The 36th COSPAR Scientific Assembly，Beijing，China，July 16 －23，2006.

［7］ Zhai G，Qiu Y，Liang B，et al.Research of capture error and error compensate for space net－capture robot ［C］. IEEE International Conference on Robotics and Biomimetics，Sanya，China，December 15－18，2007.

［8］ 于洋，宝音贺西，李俊峰.空间柔性网抛射展开过程动力学建模与仿真［J］.宇航学报，2010，31(5):1289－1296.［Yu Yang，Baoyin He－xi，Li Jun－feng.Modeling and simulation of space web projecting dynamics ［J］.Journal of Astronautics，2010，31(5):1289 －1296.］

［9］ 李京阳，于洋，宝音贺西，等.空间柔性网两种动力学模型的比较［J］.力学学报，2011，43(3):542－550.［Li Jingyang，Yu Yang，Baoyin He－xi，et al.Simulation and comparison of different dynamical models of space webs［J］.Chinese Journal of Theoretical and Applied Mechanics，2011，43(3):542 －550.］

［10］ 陈钦，杨乐平.空间绳网系统发射动力学问题研究［J］.宇航学报，2009，30(5):1829 － 1833.［Chen Qin，Yang Le－ping.Research on casting dynamics of orbital net systems［J］.Journal of Astronautics，2009，30(5):1829 －1833.］

［11］ 陈钦.空间绳网系统设计与动力学研究［D］.长沙:国防科学技术大学，2010.［Chen Qin.Design and dynamics of an orbital net－capture system ［D］.Changsha:National University of Defense Technology，2010.］

［12］ 马骏，黄攀峰，孟中杰，等.自主机动空间绳网机器人设计与动力学建模［J］.宇航学报，2013，34(10):1316－1322.［Ma Jun，Huang Pan－feng，Meng Zhong－jie，et al.Design and dynamics modeling of autonomous maneuvering tethered－net space robot system［J］.Journal of Astronautics，2013，34(10):1316－1322.］

［13］ Kumar K D. Review on dynamics and control of nonelectrodynamic tethered satellite systems［J］.Journal of Spacecraft and Rockets，2006，43(4):705 －720.

［14］ Kristiansen K U， Palmer P L， Roberts R M. Numerical modelling of elastic space tethers［J］.Celestial Mechanics and Dynamical Astronomy，2012，113(2):235－254.

［15］ Buckham B，Nahon M，Cote G.Validation of a finite element model for slack ROV tethers［C］.OCEANS 2000 MTS/IEEE Conference and Exhibition，Providence，USA，September 11－14，2000.

［16］ Förg M， Pfeiffer F， Ulbrich H. Simulation of unilateral constrained systems with many bodies［J］.Multibody System Dynamics，2005，14(2):137－154.

［17］ 陈宝林.最优化理论与算法(第二版)［M］.北京:清华大学出版社，2005:422－426.