变权组合预测模型在大坝沉降监测中的应用
2015-12-14谢朋朋
谢朋朋,黄 腾,刘 阳
(河海大学 地球科学与工程学院,江苏 南京210098)
将几种单一预测模型进行有效的组合,可以综合利用不同预测模型的优势,从而构成具有较高预测精度的组合预测模型。变权组合预测模型是提高预测精度、增强预测模型适用性的有效途径。本文将线性回归预测模型和灰色模型GM(1,1)进行变权组合,结合某大坝沉降监测实例来进行大坝位移规律的拟合和预测。
1 变权组合预测模型的建立
变权组合预测模型建立的基本思路,首先根据样本点数据建立样本点的组合优化模型,根据某种最优化原则解算各单一模型在样本点处的最优组合权系数,然后由这些权系数确定各预测模型在预测时点的权系数,从而构造出变权组合预测模型。
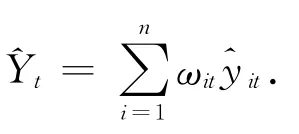
记eit为第i个预测模型在第t期的预测误差,则

其中,Yt表示第t期的实测值。记et为组合预测模型在第t期的预测误差,则

变权组合预测模型建立的关键是组合权重系数的确定,基本原则是保证样本点处的组合预测误差最小。确定变权系数的方法有3种:①以相对误差的最大值达到最小为目标确定最佳变权系数;②以绝对误差和达到最小为目标确定最佳的变权系数;③以误差平方和达到最小为目标函数确定最佳变权系数[1]。本文采用第三种方法即以组合预测模型的预测误差平方和最小为目标函数来得到组合预测优化模型:
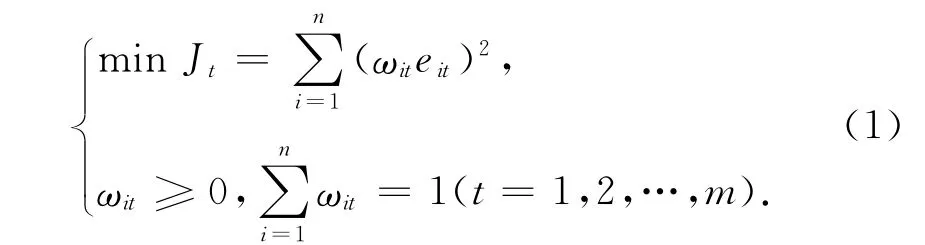
对上述模型进行求解,便可得到各预测模型在样本点处的最优加权系数ωit。
由优化模型可以得到预测模型在样本点处的最优加权系数,据此得到组合模型在预测时点处的最优组合权系数ωi,m+j(i = 1,2,…,n;j = 1,2,…,n)。目前,存在多种方法可以确定变权组合模型在预测时点处的最优组合权系数,常用的方法主要有两种[2]:

由计算过程可知,ωi,m+j满足限制条件ωi,m+j≥此种方法适用于样本量较少,或者各方法在时点序列上的权系数无明显规律性的情况。
2)利用回归法拟合权系数函数W(t),如取W(t)=b0+b1t,然后确定各预测时点处的组合预测权系数[3]。
第一步:记第i种预测模型在各样本点处的最优组合权系数:ωi1,ωi2,…,ωim;
第二步:以ωi1,ωi2,…,ωim为样本数据,采用回归模型求取权系数函数Wi(t);
第三步:利用权系数函数Wi(t),计算t=m+j时各预测方法的组合权系数函数值Wi(m+j);
2 实例分析
本文选取某大坝12号点2012年1月~2013年6月的监测数据,以2012年1月~2012年10月的监测数据为样本(见表1)建立模型并预测沉降数值,使用2012年10月~2013年6月的实测数据来进行模型精度的检验。在建模之前,采用文献[4]叙述的方法均已将非等时距序列转化为等时距序列。
根据观测数据分别建立线性回归模型和灰色模型 GM(1,1),得到

从而得到线性回归模型和灰色模型GM(1,1)在样本点处的反向预测值,如表2所示。

表1 大坝坝内12号点沉降监测实测数据

表2 模型反向预测值
由此,可得到线性回归模型和灰色模型GM(1,1)在样本点处的预测误差,见表3。

表3 预测模型在样本点处的预测误差
由于观测数据量较少,因此,在确定样本点处的最优组合权系数时,采用式(1)进行求解,由此便可得到各预测模型在预测时点的最优组合权系数,如表4所示。

表4 各预测模型在预测时点处的最优组合权系数
由此,可得到实测值和各预测模型的预测值见表5,各自预测误差见表6。

表5 实测值和各预测模型预测值
从表6可以看出线性回归模型、灰色模型GM(1,1)、变权组合预测模型的预测误差平方和分别为0.019 1、0.026 5、0.018 3。这表明变权组合预测模型在大坝沉降监测中的预测精度比任一单一模型的预测精度都要高[5-8]。
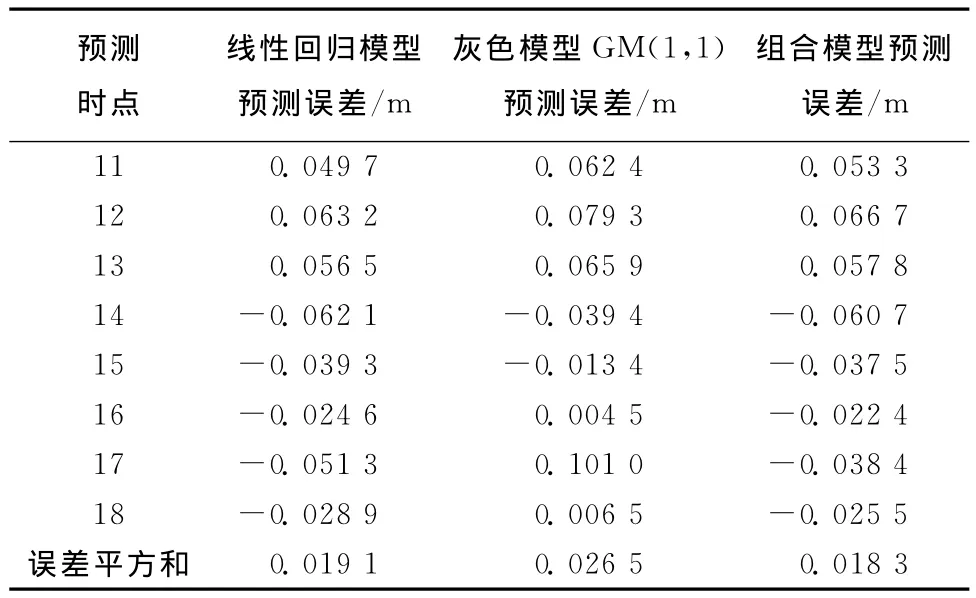
表6 各模型预测误差
3 结束语
在变权组合预测模型中权重是随时间不断变化的函数,因此预测结果更接近实测结果。结合某大坝的沉降监测实例,论证基于线性回归模型和灰色模型GM(1,1)的变权组合模型的预测精度比单一预测模型的预测精度要高。因此,利用变权组合预测模型进行大坝沉降预测是可行的。
[1]臧淑英,梁欣,冯仲科.变权组合预测模型的建立及其在区域生态风险预测中的应用[J].北京林业大学学报,2007,29(S2):203-208.
[2]王新民,崔巍.变权组合预测模型在地下水水位预测中的应用[J].吉林大学学报:地球科学版,2009,39(6):1101-1105.
[3]崔巍,王新民,杨策.变权组合预测模型在滑坡预测中的应用[J].吉林大学学报:信息科学版,2010,28(2):172-176.
[4]王磊,陈伟清,刘国献,等.灰色自回归模型的建筑物沉降预测探讨[J].测绘科学,2013,38(2):125-127.
[5]刘丹丹.灰色模型分析法在高层建筑物变形监测预测中的应用[J].测绘与空间地理信息,2014,37(2):203-205.
[6]曹昶,樊重俊.非等间距无偏GM(1,1)模型在建筑沉降预测中的应用[J].测绘工程,2013,22(6):55-57.
[7]马符讯,徐南,马成.自适应变异粒子群优化灰色模型在变形分析中的应用[J].测绘工程,2014,23(5):55-57.
[8]程晨.灰色理论和多项式拟合在地表沉降监测中的应用[J].测绘与空间地理信息,2014,37(2):220-222.
