一种基于GEP的EMD端点效应抑制方法

杨　波，李世平

（第二炮兵工程大学，陕西 西安 710025）

一种基于GEP的EMD端点效应抑制方法

杨波，李世平

（第二炮兵工程大学，陕西 西安 710025）

针对经验模态分解（EMD）在分解信号时存在的端点效应问题，为抑制端点效应对信号分析带来的影响，进一步提高EMD分解准确度，提出基于基因表达式编程（GEP）的EMD改进算法。通过仿真实验与镜像延拓等其他3种常用端点效应抑制方法作对比，并计算评价端点效应的两个指标，最后，通过这4种方法分别测量出原始信号的瞬时频率以作验证。仿真结果表明：基于GEP的EMD改进算法在分解信号后各分量两端发散程度最小，评价指标也均优于其他3种传统的改进方法，且更加准确地测量出原始信号的瞬时频率。证明该改进算法能更有效地抑制EMD端点效应，具有更高的应用价值。

经验模态分解；基因表达式编程；端点效应；瞬时频率

0　引　言

1998年，美国科学家Huang等[1-2]提出一种用于分析非平稳信号的新方法——希尔伯特-黄变换（hilbert-huang transform，HHT），HHT提供了一种巧妙的分解变换思想，它创造性地提出了内在模式函数（intrinsic mode function，IMF）的新概念（也称为本征模态函数），并提出能将任意信号分解为内在模式函数的方法——经验模态分解法 （empirical mode decomposition，EMD）。经过近些年的不断研究，EMD作为一种新的时频分析方法已经渐渐形成了独立的理论体系，在众多领域获得成功的运用。

然而，EMD分解在获得信号的瞬时平均包络时会产生端点效应[1]，给分解结果带来误差，有时甚至会造成严重失真。目前已经有不少EMD边界处理的方法，如特征波法、神经网络分析方法、镜像闭合延拓法、多项式拟合法等，这些方法都有一定效果，但同时又有明显的理论缺陷。

为更好地解决EMD端点效应，本文结合一种新型学习算法——基因表达式编程（GEP）预测来抑制端点效应对信号分析带来的影响。GEP无论是对小样本数据还是大样本数据都拥有较高的预测准确度和较快的运算速度，已经得到越来越多学者的认可，因此本文对基于GEP预测抑制EMD端点效应的方法展开研究。

1　基于GEP预测的EMD改进算法与其他延拓方法的仿真对比

1.1抑制端点效应常用方法简介

1）多项式拟合[3]：在求原始信号IMF分量的若干次循环过程中，先利用极值点数据序列两端的3个极值点求出拟合多项式，从而得到极值点序列在两端处的近似值，再求出数据序列的上下包络。

2）基于斜率的改进方法（ISBM延拓）[4]：基于斜率方法（slope based method，SBM）是一种基于信号两端附近的信号波动延伸的数据延拓方式，它通过分析信号两端端点附近极值之间的连线斜率来获取被分析的有限信号序列两端的极值延拓点，可以有效抑制EMD分解过程中产生的端点效应。本文采取的是基于SBM的改进方法（improved slope based method，ISBM）。

3）镜像延拓[5]：顾名思义，就是分别在信号两端对称位置各放一面镜子（不放在端点处），把镜子之内的信号向外映射，得到长度为两倍于镜内信号的周期信号。

1.2GEP预测简介

基因表达式编程（gene expression programming，GEP）是在传统的遗传算法（GA）和遗传编程（GP）的基础上发展起来的一种基于基因型和表现型的新型进化算法[6]。作为遗传家族的新成员，GEP不仅继承了GA定长线性编码简单快捷的特点，还具备了GP树形结构灵活多变的优势，克服了它们各自存在的不足[7]，并且比传统进化算法的运算速度要高出100～60000倍[6，8]，因此具备了更强的解决复杂问题的能力、极强的函数发现能力和很高的编程效率。标准GEP算法的基本过程如图1所示。

图1　GEP算法的基本过程

1.3基于GEP预测改进方法原理

目前处理EMD端点效应的改进方法有很多，但大多都是对信号的边界进行处理，因此，对边界处理的效果直接影响到对端点效应抑制的效果。根据这一思想，本文通过引入高准确度的GEP预测方法，首先运用GEP对信号进行预处理，通过预测分别确定左、右端之外的两个极值点，再经过传统的EMD分解方法（将信号两端视为极值点）对信号进行分解，这样就可以从源头上抑制端点效应的产生。

1.4端点效应仿真对比

本文共实现了4种端点效应改进方法：基于多项式拟合、ISBM延拓、镜像延拓、GEP的EMD端点效应改进方法的仿真，并将其仿真结果进行对比。

下面以一个非平稳仿真信号为例来阐述其端点效应。其表达式为

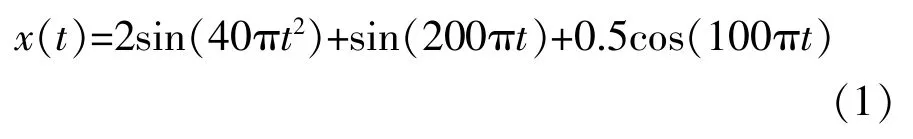
选取时间范围：0＜t＜0.216s，采样频率：fs=1kHz，抽样点为216个点。

如图2所示为，观察4种抑制端点效应方法处理后的图像（两端被圈中部分影响最大）。可以很直观地观察到：基于多项式拟合的改进方法仍然存在较为严重的端点效应，基于ISBM延拓和镜像延拓的方法在此基础上准确度得到了一定的提高，但相比来说，基于GEP的EMD端点效应的改进方法准确度最高，几乎完全抑制了EMD分解过程中的端点效应。

图2　4种改进方法分解结果

为更加清楚地展现4种改进方法之间的准确度差别，现分别考察这4种方法分解后各分量的评价指标[9]。其评价指标如下：

1）计算各个IMF分量和对应的原信号分量的相似系数ρ，比较分解前后的各分量信号与对应的原信号之间的相似度来评估端点效应的影响程度。其相似系数越大，准确度越高。

2）计算分解前后信号能量误差。其公式为

式中：RMSoriginal——原信号有效值；

RMSi——第i个IMF的有效值；

n——IMF总个数。

θ值越小，证明端点效应的影响越小，其结果如表1所示。

表1　信号分解后各方法评价指标

分析表中数据可以看出，基于多项式拟合、ISBM延拓和镜像延拓的方法，在相似系数和能量误差方面可以满足工程需要，但相比来说，基于GEP的EMD改进方法中各分量的相似系数及能量误差均优于其他方法；因此，能更好地抑制EMD方法分解信号时产生的端点效应，成为最佳选择。

2　测量瞬时频率验证改进效果

瞬时频率（instantaneous frequency，IF）是非平稳信号中的一个重要参数，并广泛应用于诸多领域，因此，瞬时频率估计也是分析非平稳信号的一项重要工作[10]。EMD分解准确度会对信号分析带来巨大影响，为进一步比较这4种改进方法中端点效应的影响程度，本文分别测量出不经端点处理的原始信号瞬时频率和其他4种改进方法处理后的原始信号瞬时频率，并作对比，如图3所示。

由式（1）可知：对信号进行瞬时频率分析可得信号的瞬时频率由100 Hz和50 Hz的恒定值和一个线性部分组成，线性部分频率从0 Hz线性增加到8.64Hz。

由图3可知，未经端点处理，测量信号的瞬时频率在边缘处有着明显且较大的波动，经端点处理后，瞬时频率测量更加准确。而相比其他3种改进方法，基于GEP的EMD改进算法在边缘处测得的瞬时频率波动最小，误差最小，而且在中间时段，瞬时频率波动变化更小，更容易观察到信号瞬时频率包含有100Hz和50Hz的恒定值和一个f=40t的线性部分。因此，进一步说明了基于GEP的EMD改进算法能够更加有效地抑制分解过程中的端点效应。

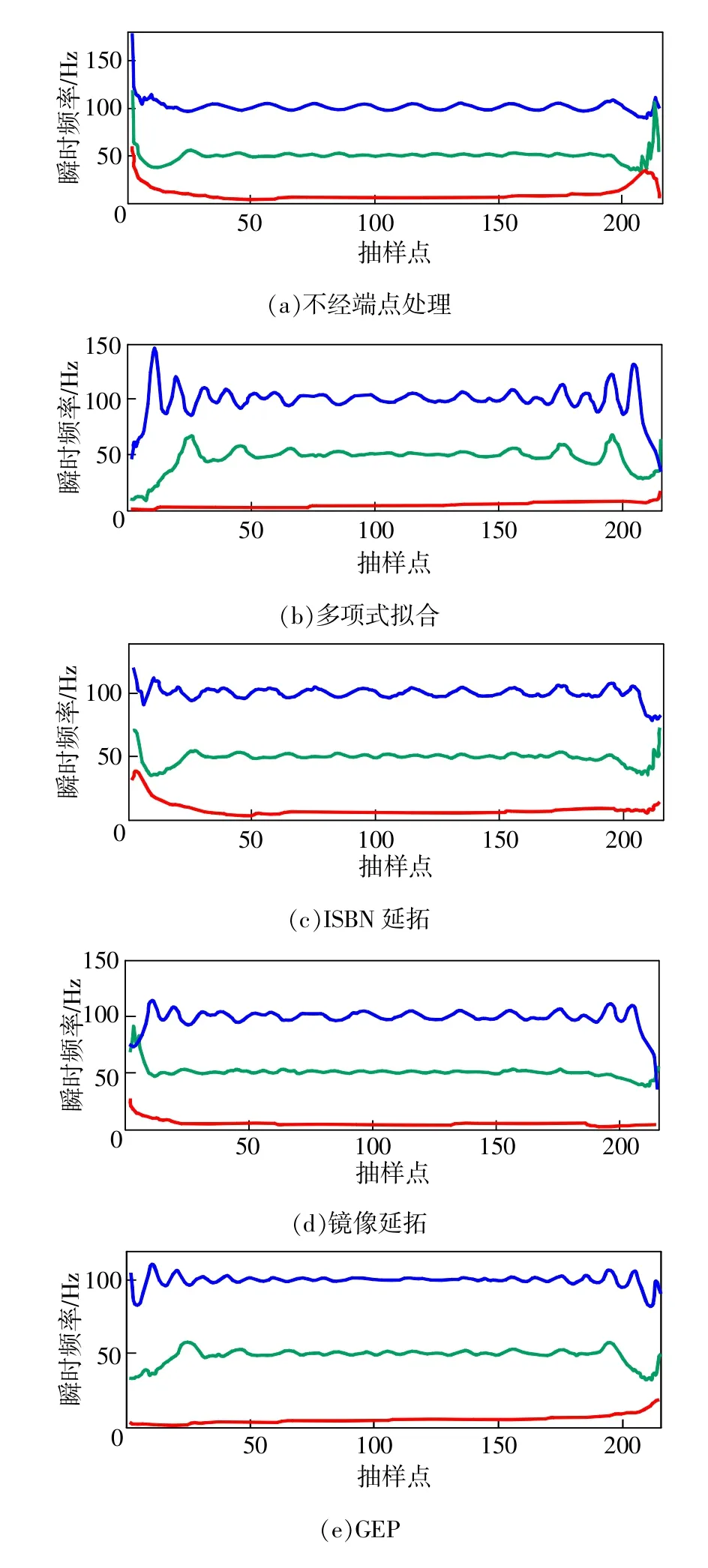
图3　4种改进方法测量瞬时频率

3　结束语

基于EMD算法运算中存在的严重的端点效应问题，本文将GEP引入到EMD算法当中，即在对信号进行分解前做预处理，采用GEP分别预测出信号两端的两个极值点，再用EMD分解信号。用该方法与其他3种传统的延拓方法进行仿真对比，从端点延拓评价指标数据可知，该方法对端点效应起到了最好的抑制效果，证实了该改进方法的可行性。然后通过测量原始信号的瞬时频率进一步验证了基于GEP的EMD改进算法抑制端点效应效果更好，且运算准确度更高，为EMD更加有效、准确地处理信号提供可靠的技术手段。

[1]Huang N E.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc R Soc Lond，1998（454）：903-995.

[2]Huang N E.A confidence limit for the empirical mode decompositionandHilbert spectral analysis[J].Proc R Soc Lond，2003（459）：2317-2345.

[3]刘慧婷，张旻，程家兴.基于多项式拟合算法的EMD端点问题的处理[J].计算机工程与应用，2004，40（16）：82-86.

[4]方琨，王渝，马利兵，等.基于RO-SBM的Hilbert-Huang变换端点效应抑制方法[J].振动、测试与诊断，2013，33（2）：319-324.

[5]Zhao J P，Huang D J.Mirror extending and circular splinefunctionforempiricalmodedecomposition method[J].Journal of Zhejiang University（SCIENCE），2001（2）：247-252.

[6]Ferreira C.Gene expression programming：a new adaptive algorithm for solving problems[J].Complex Systems，2001，13（2）：87-129.

[7]Zuo J，Tang C J，Li，et al.Time series prediction based on gene expression programming[C]∥Proceding of the 5th International Conference for Web Information Age 2004，LNCS 3129，Berlin：Springer-Verlag，2004：55-64.

[8]唐常杰，张天庆，左杰，等.基于基因表达式编程的知识发现[J].计算机应用，2004，24（10）：7-10.

[9]李建，刘伟，郭晓婷.基于EMD分解的端点延拓新方法[J].电源技术，2012，36（10）：1573-1575.

[10]张贤达，保铮.非平稳信号分析与处理[M].北京：国防工业出版社，1998:47.

GEP-based suppression of end effect in EMD

YANG Bo，LI Shiping
（The Second Artillery Engineering College，Xi’an 710025，China）

Animprovedalgorithmofempiricalmodedecomposition（EMD） basedongene expression programming（GEP）was proposed in this paper to solve the end effect existing in the signal decomposition process of EMD and to restrain the strong impact brought of end effect on signal analysis to improve further the decomposition precision of EMD.After comparing it with three other commonly-used methods namely simulation and experiment and mirror extension，the two indicators of end effect were calculated and evaluated and the instantaneous frequency of original signals was measured and verified ultimately.The simulation results indicate that the divergence degree at both ends of each component is the lowest，the evaluation indicators are more superior，and the instantaneous frequency of the original signal measured is more precise compared with the three traditional improved methods.It has proven that this improved algorithm is more precise and practical in restraining the end effect.

EMD；GEP；end effect；instantaneous frequency

A

1674-5124（2015）12-0032-04

10.11857/j.issn.1674-5124.2015.12.009

2015-06-05；

2015-08-13

杨波（1992-），男，江西南昌市人，硕士研究生，专业方向为控制科学与工程。