弹性波发生器作用下柔轮变形机理的研究

郭 刚，钟 健

（深圳职业技术学院 机电工程学院，广东 深圳 518055）

弹性波发生器作用下柔轮变形机理的研究

郭 刚，钟 健

（深圳职业技术学院 机电工程学院，广东 深圳 518055）

利用非线性有限元方法对谐波齿轮传动柔轮在弹性波发生器作用下变形与变形力进行了计算分析，得到：柔轮径向变形量与径向变形力的相关规律，柔轮初始变形力与柔轮形变基本成线性关系．计算结果与实验结果对比显示，两者趋势吻合．

非线性有限元；谐波齿轮传动；弹性波发生器

谐波齿轮传动技术是近年来发展起来的一种传动技术，其特点是用柔性元件所产生的可控波动变形实现动力的传递．与传统传动机构相比有许多独特的优点，如：运动精度高、回差小、体积小、承载能力高、传动精度和传动效率高等．目前应用最为广泛的几种波发生器均是刚性的，即发生器的长轴尺寸在工作中始终保持不变．为了实现柔轮与刚轮的轮齿间无侧隙啮合，近年专家学者提出弹性波发生器的概念[1]，这种波发生器的优点在于通过调整变形力可以改变柔轮径向变形量．

若要实现无侧隙啮合，首先要研究柔轮的变形与变形力间的关系，以利用其指导谐波齿轮的设计．为此，文献[2，3]以弹性力学为基础建立了谐波齿轮传动柔轮变形与变形力的理论计算模型，但模型中存在着简化，影响了结果的准确性．为了更加准确模拟柔轮受力变形过程得到更加准确的结果，本文利用MSC.Patran建立了谐波齿轮传动柔轮变形与变形力的非线性接触有限元计算模型，分析柔轮在弹性波发生器接触作用下的变形过程和机理，并对计算结果进行了实验验证．

1 有限元模型

根据常用的双谐波齿轮实际情况，在MSC.Patran中建立了分析模型，分析刚轮与柔轮间的相互作用．其中接触状况按非线性处理．

1.1 3D模型的建立与有限元网格划分

按照典型双谐波齿轮机型的参数进行模型的建立．柔轮所选用材料的牌号为30CrMnSiA，其弹性模量为206 GPa，泊松比取0.3．柔轮实际尺寸及柔轮轮齿部分相关参数如图1所示．

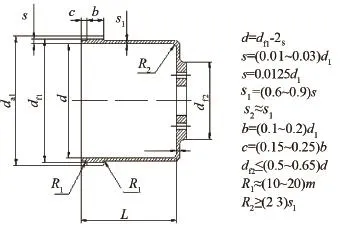
图1 杯形柔轮结构简图和尺寸

为了减少网格划分和计算所用机时，建模时忽略了柔轮底凸缘根部及齿轮根部的小圆角， 其原因在于本文中研究波发生器作用下的柔轮变形, 距离该圆角所在位置较远，圆角对计算结果影响比较小．另外，柔轮轮齿部分数量多和相对尺寸较小，划分有限元网格时，会造成相对较多的单元数量及增加网格划分的难度，而本文主要研究柔轮在弹性波发生器作用下的预变形，因此在不影响计算精度的情况下将柔轮轮齿简化为等效厚度的齿圈．

为了进一步减少计算的机时，利用模型的对称性，针对半个柔轮进行计算．网格划分使用八节点六面体实体单元，网格划分后得到约47000个网格单元．根据实际变形中波发生器相对刚度大，变形很小的特点，将波发生器的作用由一个与波发生器轮廓线和轴向长度相同的刚性圆柱面代替．有限元计算模型如图2所示．

图2 杯形柔轮模型

1.2 施加约束和载荷

1） 位移边界条件：本文中研究波发生器作用下的柔轮变形，变形主要发生在柔轮顶部开口端附近．根据实际情况和计算要求限制柔轮底部凸缘表面全部6个自由度，利用零件对称的特点，只计算一半的零件．计算时设定在对称面处周向位移为0．

2）接触边界：在MSC.Patran/Marc中设定接触边界，将柔轮设定为变形体，波发生器设定为运动刚体同时给定其径向运动规律．波发生器沿径向向外运动，与柔轮内侧接触，并使柔轮逐渐发生形变．在设定边界条件时给定其位移增量．根据问题的具体情况，计算时忽略两物体间的摩擦力．

2 实验研究

利用柔轮变形与变形力测试装置验证计算的准确性．该装置主要由3大部份组成：电机、工作台和传感器．实验装置如图3所示．

实验时，把柔轮2倒扣在固定平台1和工作台3形成的工作面上，当电机4转动时，通过丝杠副带动工作台3向右移动，由于被测件的一端被固定平台1的定位销固定住，所以柔轮发生横向变形，它的两侧端面由圆变成椭圆长轴，如图4所示．因此，实验测得的变形量是柔轮实际变形的2倍．

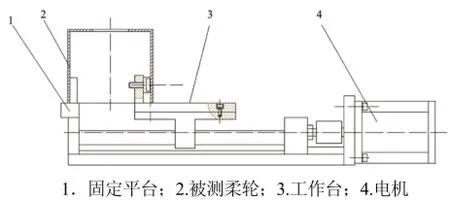
图3 实验装置图

图4 实验过程示意图

3 结果和分析

3.1 杯形柔轮位移分布

图5为杯形柔轮计算结果中沿刚体圆柱运动方向的位移分布图．变形云图显示柔轮的位移变形以波发生器接触的相关区域为界上下对称分布．杯形柔轮的变形量由顶部开口端向底部封闭端逐渐减小．波发生器的最大位移为0.39 mm．由图5可以看出，在波发生器作用下, 杯形柔轮的最大位移为0.426 mm，发生在其与波发生器接触的相关区域靠近开口端一侧．比波发生器的最大位移大．表明柔轮产生了轻微翘曲．同时最大变形区域内一些部分与运动刚体柱面已脱离接触，底部封闭端的变形最小，几乎接近为零．

3.2 杯形柔轮位移与变形力关系

图6为柔轮变形与变形力有限元计算结果曲线．图7 为柔轮变形与变形力理论计算结果曲线[2]与实验结果曲线．由图6和图7所可以看出，柔轮变形量与变形力基本呈线性关系，有限元的柔轮变形与变形力结果曲线与实验曲线比较接近，但数值略大于后者，但差距实际量值很小．有限元的柔轮变形与变形力结果曲线与理论曲线相比，更接近实验数据．这是由于在建立柔轮变形与变形力的计算模型时，理论模型为二维的，有限元为三维的，但两者都是将柔轮简化为当量光滑圆柱壳体来进行分析，而没有考虑轮齿对变形力的实际影响，造成与实验数值有差距．

图5 杯形柔轮计算结果的位移分布

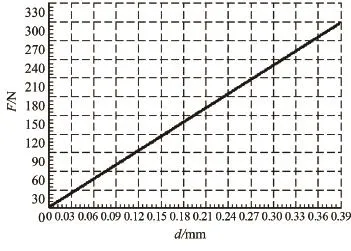
图6 柔轮变形与变形力有限元计算结果曲线

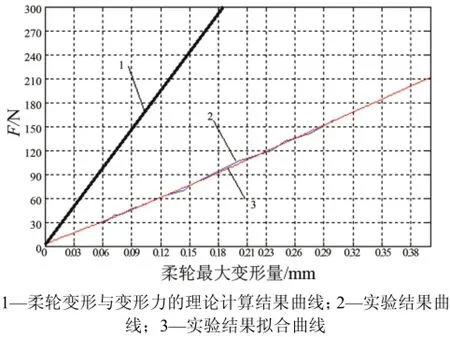
图7 柔轮变形与变形力理论计算与实验曲线

4 结 论

1） 利用MSC.Patran建立了谐波齿轮传动柔轮变形与变形力的非线性接触有限元计算模型，通过分析柔轮在弹性波发生器接触作用下的变形过程，得到较准确的柔轮径向变形量与径向变形力的关系规律．由分析结果可以得知，柔轮初始变形力与柔轮形变基本成线性关系．

2）利用柔轮进行了变形量与变形力测试实验，结果验证了柔轮有限元计算模型的正确性．

[1] 辛洪兵．研究谐波齿轮传动啮合原理的一种新方法[J]．中国机械工程，2002（3）：181-183．

[2] 李秋芳，钟健，程凯．谐波齿轮传动柔轮变形与变形力研究[J]．机械设计，2008（11）：48-50．

[3] 杨晓琦，程凯．基于MATLAB的谐波齿轮传动柔轮变形研究[J]．无线电工程，2008（7）：62-64．

Analysis of the Flexspline Distortion Under Flexible Wave Generator

GUO Gang, ZHONG Jian
（School of Mechanical and Electrical Engineering, Shenzhen Polytechnic, Shenzhen, Guangdong 518055,China）

This paper applies nonlinear FEM to calculate and analyse the flexspline distortion and the strain forces of the harmonic drive gear under flexible wave generator. Relevant principles and the conclusion of a linear relationship between the initial flexspline distortion and the strain forces are obtained. The calculation result matches with the test result.

nonlinear FEM; harmonic drive gear; flexible wave generators

TH132.43

A

1672-0318（2015）03-0022-03

10.13899/j.cnki.szptxb.2015.03.005

2014-12-23

郭刚（1964-），男，山东人，工学博士，研究方向为非线性有限元分析．